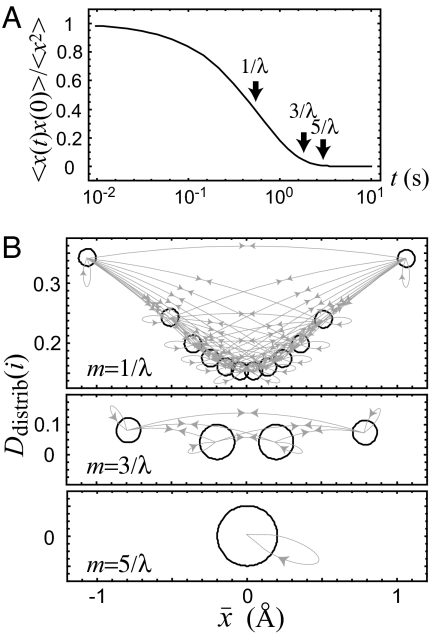
Fig. 2.
The SSNs constructed from the time series x obeying the overdamped Langevin equation on a harmonic well, dx(t)/dt = −λx(t) + R(t). Here λ = ω2/γ is the drift coefficient that characterizes the correlation time of the stochastic variable x with γ being the friction coefficient (ω is the frequency of the harmonic well, ≈1/2ω2x2). R(t) is a Gaussian random force exerted on x with mean 〈R(t)〉 = 0 and variance 〈R(t) R(t0)〉 = 2λθδ(t − t0), where θ characterizes the magnitude of the fluctuation at a given temperature. Here, θ and λ are set to be 0.19 Å2 and 1.73 s−1, respectively, by referring to the mean force potential along the “FAD-Tyr distance”and the autocorrelation of the lifetime fluctuation of the excited state of FAD (35). We discretize x into 12 symbols with variable width Δxk such that the resident probability P(xk ≤ x(t) ≤ xk + Δxk) of kth symbol sk is the same for all k. (A) The normalized aut ocorrelation function 〈x(t)x(0)〉/〈x2〉 (≃exp(−λt)) as a function of log10 t. (B) The SSNs constructed by recording every m step from the symbolic time series s with m = 1/λ, 3/λ, and 5/λ, respectively.