Spectral Dynamics of Individual Bacterial Light-Harvesting Complexes: Alternative Disorder Model

Abstract

The bacterial (Rhodopseudomonas acidophila) photosynthetic peripheral light-harvesting complex of type 2 (LH2) exhibits rich fluorescence spectral dynamics at room temperature. The fluorescence spectrum of individual LH2 shifts either to the blue or to the red during the experimental observation time of a few minutes. These spectral changes are often reversible and occur between levels of a distinctly different peak wavelength. Furthermore, they are accompanied by a change of the spectral line shape. To interpret the dynamics of spectral changes, an energetic disorder model associated with easily explainable structural changes of the protein is proposed. This model assumes that each pigment in the tightly coupled ring of bacteriochlorophylls can be in two states of electronic transition energy due to the protein-pigment interaction. The transition between these structural, and hence spectroscopic, states occurs through the thermally induced conformational potential energy barrier crossing. Although simplified, the model allows us to reproduce the bulk fluorescence spectrum, the distribution of the single-molecule spectral peak wavelength and its changes, and the statistics of the duration of the spectral states. It also provides an intuitively clear picture of possible protein dynamics in LH2. At the same time, it requires additional sophistication since it essentially does not reproduce the red occurrences of single LH2 spectra.

INTRODUCTION

In all photosynthetic organisms, light-harvesting complexes capture the solar energy and transfer the electronic excitation to the reaction center (RC), where a complicated sequence of events is initiated, involving multiple electron-transfer reactions, creation of a proton gradient across the photosynthetic membrane, and eventually leading to the synthesis of carbohydrates (1). A detailed model of the photosynthetic membrane in the purple bacteria has been obtained by means of atomic force microscopy (2,3). The RC is surrounded by the core light-harvesting complex, so-called LH1, typically absorbing at 870–880 nm, whereas a number of peripheral light-harvesting complexes, light-harvesting 2 (LH2), with absorption peaks at 800 and 850 nm, surround the LH1. Upon photon absorption by the LH2, electronic excitation is delivered to the LH1, which funnels the energy to the RC. The appearance of the crystal structures of the LH2 of Rhodopseudomonas (Rps.) acidophila and Rhodospirillum (Rsp.) molischianum (4–6) aided in the current understanding of photosynthetic light-harvesting (7–10) to a great extent. The LH2 of Rps. acidophila is a ring of nine protein-pigment subunits, each containing two α-helical transmembrane polypeptides: the α-polypeptide on the inner and the β-polypeptide on the outer side of the ring. Closer to the C-terminal the protein noncovalently binds a ring of 18 tightly coupled bacteriochlorophyll (BChl) a molecules with a center-to-center distance of ∼1 nm between neighboring pigments. This ring is responsible for the intense absorption of the LH2 peaking at ∼850 nm (B850 ring). A second ring of nine weakly interacting BChl a molecules is located closer to the N-terminal of the protein and is largely responsible for the absorption at ∼800 nm (B800 ring).

These structures, together with a vast amount of theoretical and experimental effort, have resulted in a detailed model of the energy scheme and energy transfer in light-harvesting complexes (11–18). The excitonic coupling between pigments and the static disorder of the pigment electronic transition energies (site energies) are the two basic features of this model. The energy disorder implies that, despite the circular symmetry of the antenna ring, the site energies of pigments in equivalent positions are not identical. This originates from a number of microscopic protein-pigment interactions, such as H-bonds, between the protein and the C2 acetyl carbonyl, leading to the rotation of the C2 acetyl carbonyl out of the BChl molecular plane and deformation of the BChl macrocycle, which determine the site energies of the chromophores. Since a protein is an intrinsically disordered system occurring in a number of conformational substates, the electronic transition energies are not identical for the different pigment sites.

It is generally accepted that proteins are mobile entities, undergoing a variety of structural deformations on different timescales. They move in their conformational landscape, probing different conformational substates (19). Evidence for such movements was obtained in a number of single-molecule (SM) measurements. The spectral diffusion of the B800 band in the LH2, observed at low temperature, was attributed to structural alterations (20). Spectral fluctuations of different magnitude occurring on different timescales were associated with the hierarchical structure of the conformational landscape of the protein (21). In a number of cases, large changes of the fluorescence peak wavelength (FLP), occurring between distinctly different wavelengths on a timescale of several seconds, were recently observed at ambient temperatures (22,23). These transformations were accompanied by changes of the fluorescence (FL) spectral profile shape and were associated with different realizations of energy disorder on the basis of the so-called modified Redfield theory of exciton relaxation. Slow conformational alterations of the complexes were thought to modulate the protein-pigment interactions and therefore to be the cause of the changes of the realization of energy disorder. It was also demonstrated that different observable spectral profiles correspond to diverse electronic structures of the pigment-protein and different regimes of excitation energy dynamics ranging from wavelike motion of coherently delocalized excitons to self-trapped excitation localized on one pigment site (24,25). However, these previous studies were not concerned with the mechanism of dynamics of the spectroscopic or underlying microscopic structural changes.

Ideally, we would like to perform a detailed reconstruction of the structural movements of the protein from the spectroscopic signature. However, the B850 antenna in the LH2 contains 18 pigments that are susceptible to the conformation of the surrounding protein and each of which contributes to the overall spectrum of the ring, making the interpretation of the experimental observations a rather formidable task. Therefore, the goal of this study is to attempt to interpret the observable FL spectral dynamics based on a greatly simplified model of possible protein conformations, which to our knowledge has not been performed previously. We will assume that each protein α-helix, binding one B850 BChl molecule, acquires two distinctly different structural conformations, inducing two different transition energies of the chromophore. It is noteworthy that in the ring of 18 pigments, two energy states per site will be associated with ∼15,000 different realizations of energy disorder and thus, also, different spectroscopic states, which even with reductive assumptions is a large number. Although such a model is a gross oversimplification, it allows us to reproduce the characteristic features of the spectral statistics and to determine previously unattained temporal parameters of the possible structural changes of the protein.

MATERIALS AND METHODS

Isolated LH2 complexes were immobilized on a standard microscope coverslip treated with a 0.01% poly-L-lysine (Sigma, St. Louis, MO) solution. The coverslip was used as a base for a home-designed, hermetic, temperature-controlled sample cell. A drop of a picomolar concentration of LH2 solution was placed on the coverslip, and the sample cell was assembled. After a few minutes, the cell volume was washed with deoxygenated buffer, thus removing the excess sample and submerging the immobilized single molecules in an oxygen-free environment. FL spectra were acquired with a confocal microscope based on a commercial inverted microscope (Eclipse TE300, Nikon, Tokyo, Japan) and equipped with a Plan Fluor 100×, 1.3 NA oil immersion objective lens (Nikon). The excitation source was a Ti:sapphire laser system (Mira 900, Coherent, Santa Clara, CA) producing 3-ps, 800-nm pulses with a repetition rate of 76 MHz. Spectra were acquired by dispersing the fluorescence onto a liquid-nitrogen-cooled back-illuminated charge-coupled device (CCD) camera chip (Spec10:100BR, Princeton Instruments-Roper Scientific, Tucson, AZ). CCD pixels were binned along the spectroscopic axis to yield a resolution of <1 nm. The intensities used in the experiments were from 0.13 to 1.6 kW/cm² or equivalently 500 nW to 6 μW. More than 100 complexes were measured at each excitation intensity, and for each complex a series of FL spectra was collected for 2 min with an integration time (0.5–2 s) that is dependent on the excitation power: at higher excitation intensities, shorter integration time is sufficient for the collection of the spectra with a satisfactory signal/noise ratio. For a quantitative analysis, the acquired spectra were fitted with a skewed Gaussian function, using a nonlinear Levenberg-Marquardt fitting method. Consequently, by fitting each spectrum from a series, we obtained the time traces of the amplitude, the full width at half-maximum, and the FLP wavelength with the corresponding confidence margins.

Experimental results

The experimental observations interpreted in this work have been described in great detail previously (22,23). In summary,

1. The FLP value of the single LH2 of Rps. acidophila exhibited a variety of changes of different magnitude in the course of time; whereas some of these changes appeared to be random, others occurred between quasistable levels. Quasistability implies that fluctuations of the FLP value within a separate level are distinctly smaller than the average difference between such levels.

2. Changes of the FLP value relative to the intermediate were accompanied by a change of the FL spectral shape: blue-shifted spectra were broadened and featured a regular asymmetry—a more pronounced long-wavelength tail; red-shifted profiles were broadened even more strongly and exhibited an unusually short-wavelength wing.

3. The frequency of the FLP value changes was approximately linearly proportional to the excitation intensity at ambient temperature.

Model

Our goal was to investigate possible structural changes of the LH2 and to determine their timescale. The experimentally observable FL spectral changes revealed the structural dynamics of the LH2, and to describe this dynamical attribution, we needed to develop a relevant model. The model of the B850 antenna ring needed to include the excitonic interaction between pigments, the static disorder of pigment site energies, and the coupling of the pigment electronic excitations to intra- and intermolecular vibrations/phonons, which would give rise to the so-called dynamic disorder. The FL spectral profile of the B850 was determined by the interplay of these two types of disorder (25–27). Typically, exciton models assume that structural fluctuations change the realization of the static disorder (a set of deviations of electronic transition energies of the pigments from the value in the ideally homogeneous ring), whereas parameters of the dynamic disorder remain unchanged. Therefore, the experimentally observable differences of the SM spectral line shape and the peak wavelength should be associated with different realizations of the static disorder. Transitions between different spectral states are defined by changes in the static disorder, which in turn are induced by the conformational changes of the protein in the nearest vicinity of the pigment. These changes either occur spontaneously or are light-induced due to the nonradiative relaxation of the absorbed light energy.

It is only reasonable to expect that such a complex system as LH2 should undergo a variety of structural deformations. However, in our first attempt to interpret the observed FL spectral dynamics we adopted the simplest possible disorder model, based on the assumption that each pigment can switch between two states of different electronic transition energy caused by conformational changes of the protein (Fig. 1). The simplest model demonstrating such a possibility followed from an analogy of the α-polypeptide with a tight spring with two equilibrium (conformational) states in the local environment of the protein. The aim of doing so was to explore to what extent the gross features of the observable spectral dynamics could be reproduced by the easily explainable structural changes.

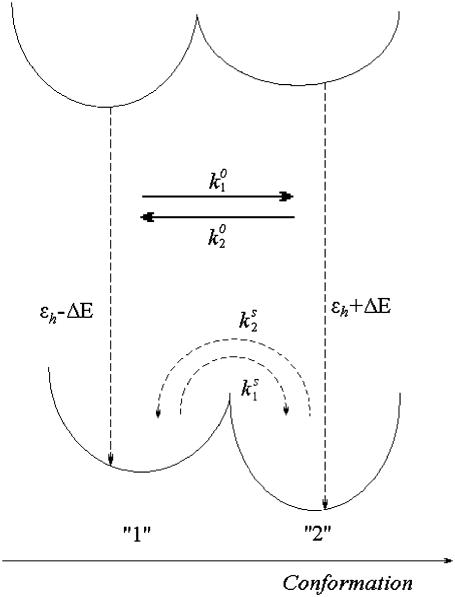
FIGURE 1.

Model of the ground- and excited-state potential surfaces of the B850 ring pigment in the surrounding protein. The potential surface is shown along the conformational coordinate of the protein. In both the ground and excited states, the protein can be in two conformational states denoted 1 and 2, separated by an energy barrier. In the absence of light, excitation transitions between the conformational states are spontaneous and occur in the ground state (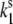 and 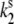). When the pigment is excited, additional light-induced transitions (with rates 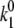and 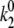) occur either in the excited state or in the initial moments after the excitation relaxation.

Below, we calculate the excitonic energies and the wavefunctions associated with the specific realization of the static disorder by diagonalizing the relevant exciton Hamiltonian. The realization of the disorder changes with the rate dependent on the outcome of this calculation. Diagonalization of the Hamiltonian is repeated with the new value of the static disorder resulting in a new rate of the subsequent spectra change. This procedure is iterated a number of times to obtain an associated spectral time trace.

Fluorescence profile

Here, we apply the exciton theory, taking into account the exciton-phonon coupling and static diagonal disorder (28–30):

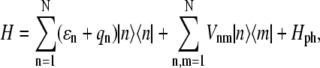(1)

where ɛ_n is the electronic transition energy, q_n are collective coordinates of the thermal bath describing the modulations of the diagonal energies in molecular representation, 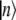and 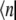are the ket and bra vectors, respectively, of the nth BChl molecule in the B850 ring. Matrix elements, V_nm, denote the energies of the dipole-dipole coupling between the nth and the mth pigments. These values can be calculated from the structural data of the LH2 of Rps. acidophila (4) and were determined experimentally (15). H_ph is a free phonon (bath) Hamiltonian.

Conventionally, in the ensemble of the LH2 complexes the pigment excitation energy ɛ_n is taken from the Gaussian distribution with the mean value ɛ_h, where the subscript denotes the helix binding the pigment (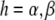). According to our model, we will consider the spectral dynamics of a single LH2 complex by assuming that any of the pigment molecules can reside in two energy states:

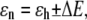(2)

where ΔE is half of the electronic transition energy difference between the two states characteristic of a particular BChl molecule in the B850 ring, as shown in Fig. 1.

The modified Redfield theory is based on the approach when the diagonal term of the exciton coupling with the bath, q_n, can be taken explicitly (31). This interaction is reflected in the correlation function or spectral density function (SDF) in the site representation (30):

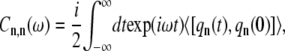(3)

where the bath average and the time evolution are taken with respect to a free phonon Hamiltonian H_ph. Initially, we assume that the SDFs for all BChl molecules are identical and uncorrelated (therefore, the site-related indexing can be omitted in Eq. 3). The possible effect of correlation will also be discussed later. To determine the SDF in this case, the overdamped Brownian oscillator will be assumed (30):

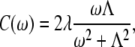(4)

where λ is the reorganization energy of the BChl molecule in the surrounding protein, and Λ is the damping parameter (reciprocal relaxation time). By introducing the exciton states,

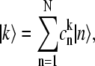(5)

where 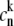is the wavefunction amplitude expressing the participation of the nth excited molecule in the kth exciton state, the Hamiltonian in Eq. 1 can be diagonalized in the exciton representation:

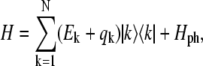(6)

where the transition energy of the kth exciton level, E_k, the collective nuclear coordinate, q_k, and the associated correlation function, 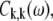in the exciton representation relate to the corresponding entities in the site representation as follows (28):

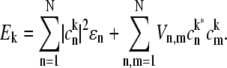(7)

The cumulant expansion method provides the expression for the FL spectrum, which is defined as a sum of the thermally weighted line shape functions of the exciton states, 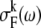(30,31):

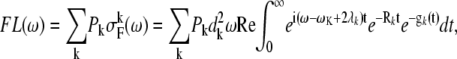(8)

where 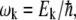P_k is the population of the exciton states in the thermal equilibrium, 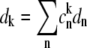is the transition dipole moment of the kth exciton state, which is directly related to the transition dipole moment of all pigments (d_n is the transition dipole moment of the nth pigment) in the aggregate, λ_k is the reorganization energy, R_k is the Redfield parameter of the excitation relaxation, and g_k(t) is the spectral line-broadening function of the kth exciton state. The reorganization energy of the kth excitonic state is related to the reorganization energy of a single pigment λ: 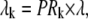where PR_k is the participation ratio (or an inverse delocalization length):

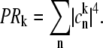(9)

The line-broadening function is given by

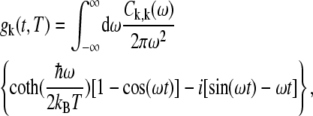(10)

where 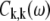is the correlation function (or SDF) in the exciton representation, defined by Eq. 7.

Modeling of disorder

To account for the presence of conformational states of the protein let us assume that the electronic states of each BChl molecule are characterized by (at least) two minima along some generalized conformational coordinate (Fig. 1). The resulting barriers will determine the timescales of the conformational changes of the protein in the excited state as well as in the ground state. The two potential energy minima are denoted as “1” and “2” (see Fig. 1), with the former assumed to be associated with the lower electronic excitation energy, as defined in Eq. 2.

A transition between the two conformational states occurs due to the thermally induced potential energy barrier crossing, or it can also be light-induced as a result of dissipation into the surrounding protein scaffold. In the first case, the protein temperature is that of the ambient, whereas in the case of light-induced changes the protein might be locally heated and/or the characteristic energy barrier separating the potential energy minima could differ from that of the spontaneous transition. Thus, this rate is sensitive to temperature and is linearly dependent on small changes of temperature. In a typical SM experiment, the LH2 complex is excited ∼10⁷ times/s. More than 90% of the absorbed photons are dissipated in the protein scaffold and further, to the surroundings of the complex. The calculated average temperature change of the complex in such a dynamic equilibrium is negligible (∼10⁻⁴ K for 6 μW of the excitation power). If the complex is adiabatically isolated, the expected temperature increase is ∼2 K and it is reached in ∼60 ps. Such a temperature increase would not be associated with a noticeable enhancement of the probability of overcoming the energy barrier. However, the probability of the transition might be enhanced at early times after the internal conversion before the thermalization is reached, i.e., when the pigment-protein is heated locally. In this case, the frequency of conformational transitions should be linearly dependent on the frequency of molecule excitation events or the excitation intensity, as was observed experimentally (22). The thermally induced barrier crossing mechanism is also consistent with the observed fast jumps between long-lasting spectrally distinguishable states. Spontaneous transitions are also taking place, as demonstrated experimentally (32). Thus, the total rate of the transition can be defined phenomenologically as

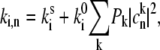(11)

where 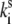is the rate of spontaneous transition and is the fitting parameter of the light-induced transition rate, which is assumed to be site-independent. 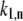is defined as the transition rate of the nth pigment in the ring from state “1” to state “2” and 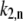is the transition rate in the reverse direction. The second term in Eq. 11 determines the rate of the light-induced change of the protein conformation. It is proportional to the sum of the contributions of the excited pigment to the exciton states weighted with the thermodynamic population of those states. It is also dependent on the frequency of the excitation of the complex, which is accounted for by 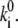The rate of spontaneous changes, 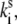is determined by the height of the energy barrier separating states 1 and 2.

Transition rates determined by Eq. 11 are defined for a particular realization of the static disorder. However, the barrier crossing is a stochastic process, and it should be taken into account by calculating the time span in a particular conformational state. If the transition rate is constant, the transition probability for the nth pigment in the ith conformational state is given by

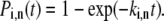(12)

Thus, the transition moment can be determined by generating the random transition probability from the uniform distribution [0…1].

To start calculating, the initial realization of the static disorder is generated randomly. After diagonalization of the exciton Hamiltonian (Eq. 1), the transition rates 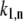and 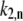are calculated in accordance with Eq. 11, and the transition time for every pigment is defined with the help of Eq. 12. The electronic excitation energy of the pigment with the smallest transition time t₁ is assumed to switch into its supplementary state, thus resulting in changes in the realization of the energy disorder in the ring. Subsequent diagonalization of the exciton Hamiltonian determines new energy states and, consequently, new transition rates for the pigments, according to Eqs. 11 and 12. The new transition moment for a particular pigment after accomplishment of the previous transition is calculated by taking into account the modified exciton spectrum. The transition moments for the rest of the pigments are also recalculated using the transition probabilities generated initially and the modified expression for the transition moment is given by

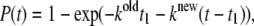(13)

where t₁ is the time span of the state, related to the former realization of the disorder.

It is noteworthy that two realizations of the static disorder, if they are not identical, according to the symmetry operation correspond to different spectral states. According to our model, the conformational change occurs for only one pigment at a time; thus, two consecutive realizations of the disorder cannot be connected by a symmetry operation. Therefore, each change in diagonal disorder produces changes in the exciton spectrum, and the described procedure of repetitive Hamiltonian diagonalization and subsequent calculation of the transition moments result in the FL spectral time trace.

RESULTS

To calculate the fluorescence spectrum, the model parameters have to be accounted for. The strength of the resonance interactions determining the exciton Hamiltonian can be defined from the fit of the ensemble-averaged LH2 absorption, and LD and CD spectra (15,33). We denote two neighboring dimeric subunits 1 and 2 in the B850 ring, and pigments that are bound to the α and β polypeptides in the ith subunit as iαiβ. Then the resonant interaction strengths between pigments 1α1β, 1β2α, 1α2α, 1β2β, and 1α2β are 291, 273, −50, −36, and 12 cm⁻¹, respectively. The Q_y transition energies for BChls bound to the α- and β-polypeptides are 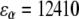cm⁻¹ and 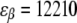cm⁻¹, respectively, and the Brownian oscillator damping constant (used in the expression of the line-broadening function) is chosen as Λ = 10¹³ s⁻¹. The relaxation parameters R_k = 16, 29, 44, and 57 ps⁻¹ were taken for k = 0, −1, 1 and −2 states, respectively, as defined to obtain the relevant bandwidths of the components of the fluorescence spectra and to describe kinetics of the transient spectra (22,25).

For the sake of simplicity the results obtained at the highest excitation intensity (at 6 μW) can be fit by neglecting the spontaneous transitions defined in Eq. 11, i.e., assuming that 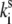= 0. Evidently, the spontaneous transitions should be taken into account by fitting the data at lower excitation intensity (at 2.5 μW). When the spontaneous transitions are neglected, the adjustable model parameters are the transition rates 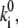the static disorder ΔE, and the reorganization energy λ. The shape of the spectral trace and the spectral statistics depend on the ratio of the transition rates 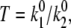whereas the absolute values of the transition rates determine only the timescale of the spectral changes.

Average fluorescence spectrum

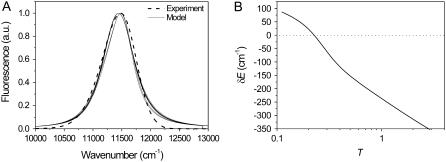
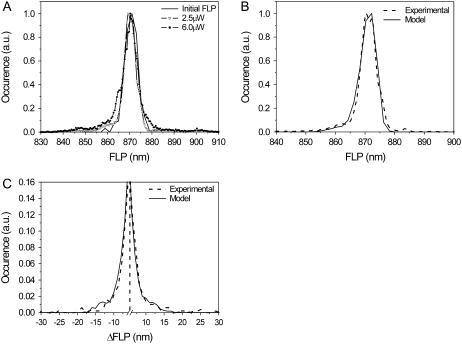
The calculated spectrum averaged over a number of disorder realizations is compared with an average of the measured FL spectra of a single molecule obtained at the highest excitation intensity, 6 μW (Fig. 2 A). The mean-square displacement between the two averaged spectra can be chosen as a fitting criterion. The model spectrum is averaged over 500 realizations of the disorder, since further increase of this number does not affect the average spectral shape considerably. The average FL spectrum can be reproduced with T in the 0.1–9 range. For any T value in this interval the acceptable ΔE and λ can vary by ∼100 cm⁻¹. When the ratio of the transition rates is low (T ≈ 0.1–0.2), both ΔE and λ values have to be large, in the range of 300–400 cm⁻¹. When T approaches unity, ΔE has to be lowered to 100–200 cm⁻¹ with simultaneous λ decrease from 380 cm⁻¹ when ΔE = 100 cm⁻¹ to 220 cm⁻¹ when ΔE = 200 cm⁻¹. Further increase of T is not associated with considerable changes of ΔE or λ. It is noteworthy that for a better fit, all excitonic levels are additionally shifted by an amount dependent on T, as shown in Fig. 2 B.

FIGURE 2.

(A) A few best fits of the bulk fluorescence spectrum. The experimental spectrum is an average over time and measured complexes. Model parameter sets corresponding to different calculated spectra are {T = 9, ΔE = 160 cm⁻¹, λ = 220 cm⁻¹}, {T = 0.5, ΔE = 200 cm⁻¹, λ = 380 cm⁻¹}, {T = 0.5, ΔE = 220 cm⁻¹, λ = 340 cm⁻¹}, {T = 0.33, ΔE = 260 cm⁻¹, λ = 380 cm⁻¹}, and {T = 0.1, ΔE = 360 cm⁻¹, λ = 400 cm⁻¹}. (B) The T (transition rate ratio) dependence of an additional shift, δE, of all excitonic energies, which is introduced for a better fit. This shift is weakly dependent on λ and ΔE.

FLP statistics

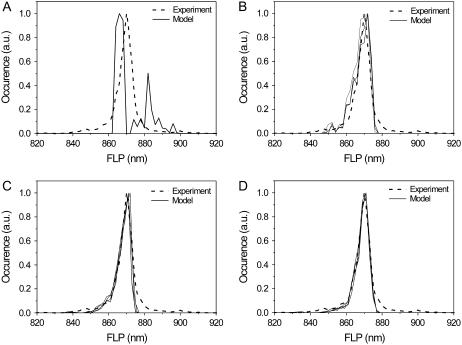
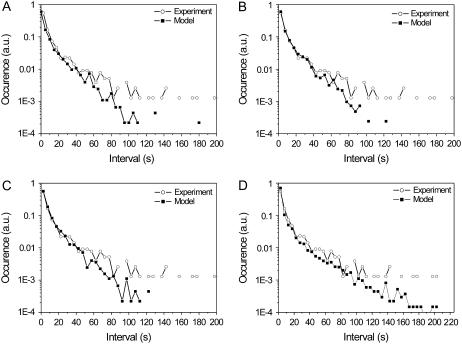
The averaged FL spectrum is not very sensitive to variation of the model parameters due to averaging over many realizations of the diagonal disorder. This averaging is the result of the SM spectral characteristics (e.g., FLP, the full width at half-maximum) and spectral heterogeneity of different complexes in the ensemble. For instance, an average of narrow SM spectra distributed over a wide range of FLP values might be similar to an average of wider spectra distributed over a narrow FLP interval. It can be expected that the statistics of the spectral parameters should reflect the statistics of the diagonal disorder. Thus, the FLP statistics was used as a second criterion to adjust the model parameters. Ten thousand model spectra were used to reach the convergent FLP statistics. It is noteworthy that the FLP statistics was rather sensitive to the ratio of the transition rates T. The calculated distribution of the FLP statistics is close to the experimental data (Fig. 3) if 0.33 < T < 2. When T > 2, the FLP distribution features several peaks and thus significantly differs from the experimental results. In the case where T < 0.33, the major 870-nm peak in the calculation is too narrow in comparison with the experimental observations and the wings of the distribution are also missing.

FIGURE 3.

The statistics of the fluorescence peak wavelength. Experimental statistics are obtained under 6.0 μW of the excitation intensity. Conformational transitions taken into account in the calculation are light-induced only. (A) T = 9, ΔE = 200 cm⁻¹, λ = 280 cm⁻¹. (B) T = 1, ΔE = 160 cm⁻¹, λ = 280–320 cm⁻¹. (C) T = 0.5, ΔE = 200 cm⁻¹. λ = 280–340 cm⁻¹. (D) T = 0.5, ΔE = 240–260 cm⁻¹, λ = 360–380 cm⁻¹.

Restrictions for the disorder and for the reorganization energy are also obtained from fitting the FLP statistics. Namely, the acceptable values are ΔE = 240–260 cm⁻¹ and λ = 360–380 cm⁻¹ when T = 0.33, whereas ΔE = 180–220 cm⁻¹ and λ = 300–380 cm⁻¹ when T = 0.5, and ΔE = 100 cm⁻¹ and λ = 380–400 cm⁻¹ when T = 2.

Statistics of the FLP changes

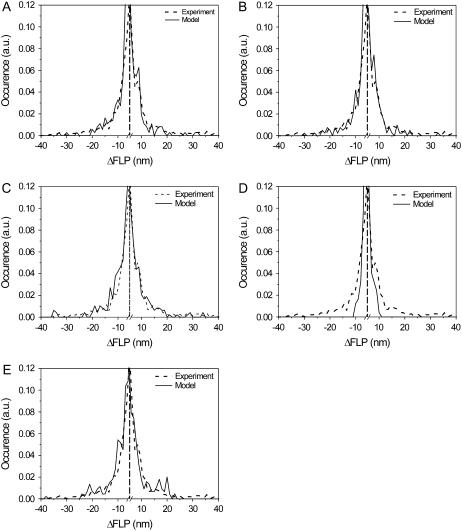
The fit of the experimental distribution of spectral shifts >5 nm (an arbitrarily set threshold) is performed with the best parameter sets obtained from the previous fitting steps. After this fitting step, the model parameters are constrained to λ = 340–380 cm⁻¹, ΔE = 200–260 cm⁻¹, and T = 0.5–0.3. Other parameter sets do not produce large (>20-nm) spectral shifts, as observed in the experiment, or they fit the experimental statistics poorly. The best results are presented in Fig. 4, A–C. Two unsatisfactory cases are also shown for comparison (Fig. 4, D and E). In addition, the energy shift δE = −100cm⁻¹ is also assumed for better fitting (Fig. 2 B).

FIGURE 4.

Statistics of the FLP shifts. The experimental data are obtained under 6.0 μW excitation intensity. (A–C). Best results of the calculation. (D and E) Worst results are shown for comparison: distribution is too narrow when T is large (D) and it has excessively pronounced wings in the region of ∼20 nm when disorder values are too large (E). Parameters are (A) T = 0.5, ΔE = 200 cm⁻¹, λ = 380 cm⁻¹, (B) T = 0.33, ΔE = 220 cm⁻¹, λ = 340 cm⁻¹, (C) T = 0.5, ΔE = 220 cm⁻¹, λ = 340 cm⁻¹, (D) T = 2, ΔE = 100 cm⁻¹, λ = 400 cm⁻¹, and (E) T = 0.33, ΔE = 280 cm⁻¹, λ = 340 cm⁻¹. Vertical dashed line denotes break position.

Transition rates

Comparison of the calculated and measured frequencies of spectral jumps (the number of spectral shifts per unit time) yields the absolute magnitude of the transition rates, i.e., 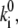in combination with the values of the static disorder, the reorganization energy, and the ratio between the transition rates that were already adjusted in previous sections. As already noted, we consider only jumps >5 nm. Let us define the rate as, 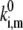from model calculations, and the characteristic rate of the spectral jumps deduced from the experiment as 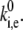Then the ratio between those rates should satisfy

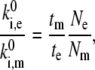(16)

where t_m and t_e and N_m and N_e are the durations of the model and experimental time traces (Fig. 5) and the number of spectral jumps per time trace, respectively. This relationship is obvious if we consider that the frequency of spectral jumps is proportional to the pigment transition rates, 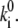The obtained transition rates are 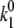≈ 0.4–0.5 s⁻¹ and 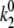≈ 0.9–1.2 s⁻¹, depending on the chosen parameter set.

FIGURE 5.

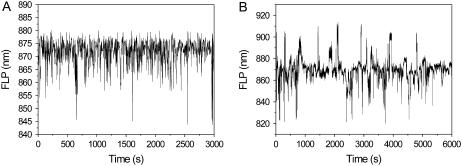
Time traces of fluorescence peak wavelength. (A) Model results. (B) Experimental results showing an average of 120-s time traces of a number of different complexes.

Experimental spectra were measured with a precision of 0.5 s to account for the integration time. If spectral changes are faster than the integration time, they are averaged out. In that case, Eq. 16 will not be valid, because the number of detected spectral jumps, N_e, will be lower than the real value, and thus, 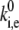is underestimated. The calculated SM spectra, then, also must be averaged over the experimental integration time. Such averaging would also significantly affect the FLP and ΔFLP distributions, making both narrower.

To verify whether the predicted spectral jumping frequency is lower than the experimental integration time, the average delay between the spectral jumps was calculated for the obtained rate values 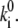Averaged time intervals appear to be in the range of 1.6–1.8 s for the best sets of parameters. Since they are longer than the spectral integration time, i.e., 0.5 s, the applied calculation procedure and its results seem to be adequate.

As is evident from Fig. 6, the statistics of the calculated durations of fluorescence at the same state is close to the statistics from the experimental data at shorter times. However, the histograms slightly diverge when the value of the time interval exceeds 70 s. Again the spectral shifts, ΔFLP < 5 nm, are neglected in this calculation.

FIGURE 6.

Statistics of time intervals between the spectral jumps. (A) T = 0.33, ΔE = 260 cm⁻¹, λ = 380 cm⁻¹, (B) T = 0.5, ΔE = 200 cm⁻¹, λ = 380 cm⁻¹, (C) T = 0.5, ΔE = 220 cm⁻¹, λ = 340 cm⁻¹, (D) stretched exponential results: ΔE = 200 cm⁻¹, λ = 380 cm⁻¹, α₁=1.2e-3 s⁻¹ α₂ = 8.7e-4s⁻¹ β = 0.2.

Spontaneous conformational changes

From a comparison of the calculated and experimental FLP time traces (Fig. 5), it is evident that the red spectral realizations are not satisfactorily reproduced. By taking into account the spontaneous conformational changes, this discrepancy can be slightly improved (34). The ratio of the spontaneous transition rates, 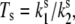can be determined by fitting the initial FLP distribution (Fig. 7 A) and the bulk FL spectrum: T_s should be chosen from the range 0.33–1, ΔE ≈ 150–300 cm⁻¹ and λ ≈ 350–500 cm⁻¹. The result is insensitive to the absolute values of 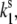which defines the timescale of the spontaneous transitions.

FIGURE 7.

(A) Experimental distribution of initial FLP values and FLP statistics obtained for two different excitation intensities. (B and C) Calculated FLP (B) and ΔFLP (C) statistics, with spontaneous transitions included. Model parameters used for the calculations are T = 0.5, T_s = 0.5, ΔE = 200 cm⁻¹, λ = 380 cm⁻¹, 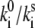= 50. Additional spectral shift of the exciton levels is δE = −110 cm⁻¹. The experimental excitation intensity in B and C is 2.5 μW. Vertical dashed line denotes break position.

The statistics of the light-induced FLP changes is much more sensitive to the model parameters, and a reasonable fit of the experimental data, obtained at 2.5 μW of the excitation intensity (Fig. 7), is achieved with the following model parameters: T = 0.5, T_s = 0.5, ΔE ≈ 190–220 cm⁻¹, λ ≈ 340–380 cm⁻¹, 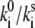≈ 30–50. Excitation energies of all BChl molecules are shifted by −110 cm⁻¹ to get a better fit of the average FL spectrum. The absolute values of the transition rates can be calculated as described above. We get 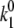= 0.18 s⁻¹, 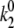= 0.37 s⁻¹, 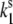= 0.0037 s⁻¹, and 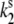= 0.0074 s⁻¹. Comparison of 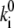calculated for the 2.5-μW excitation intensity with that calculated for 6.0 μW ( 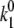≈ 0.4–0.5 s⁻¹ and 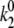≈ 0.9–1.2 s⁻¹, respectively) shows that the rates of the light-induced transitions are indeed linearly dependent on excitation intensity.

DISCUSSION

We demonstrated that an alternative disorder model, assuming that each pigment molecule in the antenna ring may be in two possible energy states, reproduces the bulk FL spectrum with the spectrum of the single LH2 averaged in time, as well as the statistics of the FLP distribution. It also explains the fluorescence changes, attributing them to conformational motions of the protein. In general, the conformational changes of the protein are represented as a diffusive motion between the local minima in the multidimensional energy landscape; therefore, the two-state model should be considered as an evident simplification. However, it provides an intuitively clear picture of possible protein motions, attributing them to the α-helix movement between the two equilibrium positions with the potential energy barrier in between. Moreover, it also resembles the two-level model used to describe the hole-burning and spectral diffusion (35). The exponential kinetics, evidently neglecting the details of the spectral diffusion, was assumed to characterize the transition between two states (Eq. 12). To take the effect of spectral diffusion through multiple pathways into account, the stretched exponential transitions between relevant states should be taken into consideration. In this case, Eq. 12 is substituted by 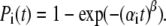According to the relevant numerical analysis, the statistical distribution of the fluorescence spectral parameters and fluorescence bulk spectrum is weakly dependent on the parameters of the stretched exponential. However, the stretched exponential approach leads to a better fit of the time interval statistics (Fig. 6 D), when the stretching parameter is β = 0.1–0.3.

The calculated averaged fluorescence spectrum has a slightly more pronounced blue wing than that obtained from the experimental data. This might be due to fitting specificity, since some model parameters were chosen as fixed and were not varied by fitting. For instance, the relaxation rates of the excitonic states R_k and the damping parameter of the Brownian oscillator Λ were assumed to be nonvariable and taken to be the same as in Rutkauskas et al. (23), although slight modificaton of these parameters would have a definite impact on the FL spectrum. Since relaxation was defined from fitting of the bulk FL and absorption spectra of the LH2, assuming the Gaussian static disorder model, these values might not be fully appropriate in the two-state disorder model. To find a better set of those parameters, the bulk LH2 absorption and FL spectra should be recalculated within the frame of the suggested alternative disorder model by taking the relaxation rates as additional fitting parameters. However, such a recalculation is not within the scope of this work; it would make the model too complicated with too many adjustable parameters. On the other hand, the molecular reorganization energy related to the strength of coupling of the electronic transition to the phonon bath was taken as an adjustable parameter and was found to be within the range 340–380 cm⁻¹, which is close to previously reported values for SM experiments obtained using the Gaussian static disorder (22). It is noteworthy that this value is several times larger than the reorganization energy of the BChl molecule in solution, indicating a substantial effect of the pigment-protein interaction. The large reorganization energy value is also required to justify the strong exciton-phonon coupling when attributing the fluorescence spectrum to the self-trapped excitons (24).

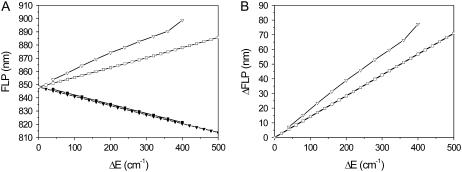
In the model described in this article, every pigment can attain two transition energy values. This leads to 2¹⁸ possible realizations of diagonal disorder and to ∼15,000 realizations, which remain not connected via symmetry operations. Realization of the disorder, together with the reorganization energy, determines the spectral properties (e.g., FLP). This implies that the FLP is restricted irrespective of the rules for the diagonal disorder generation for given ΔE and λ values. The model described here does not reproduce the red spectral realizations for measurements at 6.0 μW excitation intensity. It might be that these red-shifted spectra cannot be reproduced by any of the 15,000 realizations, or that the needed realizations have very low probabilities. The dependences of the extreme blue and red FLP on ΔE are plotted for several λ values in Fig. 8 A. It appears that the bluest state corresponds to an almost homogeneous ring, with all pigment site energies shifted to the blue. The reddest states occur when several neighboring pigments are in state 1 and the rest are in state 2, which is the cause of a significant localization of the excitation and, hence, an enhanced exciton-phonon coupling, which leads to a spectral red shift even larger than in the homogeneous ring with all pigment site energies uniformly shifted to the red.

FIGURE 8.

FLP wavelength limits for the two-state model. (A) The reddest and bluest states were calculated on the assumption that all pigments are in state 1 (open squares) or 2 (solid squares). In such a case, the ring is homogeneous. The reddest (open triangles) and bluest (solid triangles) states without making this assumption were calculated with reorganization energy value λ = 380 cm⁻¹ and an inhomogeneous ring. (B) The difference between the bluest and reddest calculated FLP values (homogenenous ring, squares; inhomogeneous ring, triangles).

Experimental FLPs are distributed in the 820–917 nm range. As shown in Fig. 8, such extremely shifted spectra are not attained with the disorder ΔE < 500 cm⁻¹. The value of the disorder calculated from the fit is only ΔE = 200 cm⁻¹, which corresponds to the most extreme spectral occurrences differing by ∼40 nm. This implies that the two-state disorder model seems to be oversimplified and should be modified to improve the results.

The calculated FLP is limited to the interval of 842–882 nm, with the highest density of states in the vicinity of 870 nm falling down sharply when FLP > 880 nm, and FLP < 865 nm for the chosen values of parameters. No enhancement of the red side of the FLP distribution is obtained by taking into account the correlation between the transitions in the pigments irrespective of the strength of correlation. Such enhancement can be reached only by assuming that two neighboring pigments in opposite states (one in state 1 and the other in state 2) change their states simultaneously. Since the “reddest” realizations correspond to strong localization of the excitation on one or several pigments, this rule should have the effect of preserving the reddest realizations. Some improvement of the model can be evidently reached by assuming additional inhomogeneity for all molecular transitions or suggesting more than two conformational states for each pigment molecule, with their reflection in the molecular electronic transitions.

Another cause of the rarity of the red FLP occurrences is related to the way the disorder realizations are generated. As mentioned previously, the red spectral states are associated with significant exciton localization or with a large participation ratio, and can occur if several neighboring pigments are in state 1, which results in lowering of the excitation energy. However, as the excitation is localized on the red pigments, there is a high probability that they will undergo a light-induced spectral change. This makes the formation of red pigment “pockets” and red spectral realizations unlikely. However, introducing light-independent spontaneous conformational changes slightly improves the red side of the FLP statistics. Moreover, recent experiments reinforce the significance of the spontaneous spectral changes (32).

The model presented here assumes the same characteristics of the exciton-phonon coupling in each conformational state. Evidently, additional variable values of the reorganization energies in each conformational state of the molecule could give additional possibilities by reaching the most red fluorescence bands.

CONCLUSIONS

Here, we proposed a new disorder model of the bacterial photosynthetic peripheral light-harvesting complex based on the assumption that inhomogeneous disorder originates from the conformational states for each pigment molecule. The protein-pigment interactions modify the pigment transition energy. Since the protein moves in the conformational potential energy landscape, probing different structural or conformational substates, pigment transition energy changes accordingly. This alternative disorder model successfully reproduced the bulk FL spectrum (B850 band). It also reproduced statistics of the SM fluorescence spectral peak wavelengths, which is more sensitive to the disorder model than the bulk spectrum. This model also explained the FL spectral dynamics of single LH2 complexes, namely, the statistics of spectral shifts and lifetime distribution of spectral states. The timescale of protein conformational dynamics, both spontaneous and light-induced, could also be determined.

At the same time, this model has several drawbacks. The red part of the FLP statistics is underrepresented and the range of occurrences of FL peak wavelengths is too narrow compared to the experimental results. Therefore, this simple disorder model calls for additional degrees of sophistication.