Simulating Dark Expressions and Interactions of frq and wc-1 in the Neurospora Circadian Clock

Abstract

Circadian rhythms are considered to play an essential part in the adaptation of organisms to their environments. The occurrence of circadian oscillations appears to be based on the presence of transcriptional-translational negative feedback loops. In Neurospora crassa, the protein FREQUENCY (FRQ) is part of such a negative feedback loop apparently by a direct interaction with its transcription factor WHITE COLLAR-1 (WC-1). Based on the observation that nuclear FRQ levels are significantly lower than nuclear WC-1 levels, it was suggested that FRQ would act more like a catalyst in inhibiting WC-1 rather than binding to WC-1 and making an inactive FRQ:WC-1 complex. Intrigued by this hypothesis, we constructed a model for the Neurospora circadian clock, which includes expression of the frq and the wc-1 genes and their possible interactions. The model suggests that even small amounts of nuclear FRQ-protein are capable of inhibiting frq transcription in a rhythmic manner by binding to WC-1 and promoting its degradation. Our model predicts the importance of a FRQ dependent degradation of WC-1 in closing the negative feedback loop. The model shows good agreement with experimental levels in nuclear and cytosolic FRQ and WC-1, their phase relationships, and several clock mutant phenotypes.

INTRODUCTION

Circadian oscillators are important in the daily and seasonal adaptation of organisms to their environment (1–4). These oscillators are assumed to act as timing devices (“clocks”) and induce, probably due to measurement of the day length, daily and seasonal processes that are crucial for the organism's environmental adaptation and survival (2).

In many organisms, the circadian oscillator is composed of a transcriptional-translational negative feedback loop of certain clock genes (1,5), which sometimes are also associated with the occurrence of positive feedback loops (6). In the model organism Neurospora crassa (7), the transcriptional translational negative feedback loop of the frequency (frq) gene has been found to be essential for its circadian conidiation rhythm (8,9). The frq transcription is activated by the WHITE COLLAR complex (WCC), a heterodimer of the zinc-finger proteins WC-1 and WC-2, where WC-2 is expressed at a constant and abundant level in excess over WC-1 (10–12). The protein FREQUENCY (FRQ) promotes the synthesis of WC-1, leading to a positive feedback (6,13). The negative feedback occurs by the translocation of cytosolic FRQ into the nucleus where FRQ inhibits its own transcription, apparently by interacting with the WCC and with the help of an RNA helicase, the “FRQ-interacting RNA helicase”, FRH (14). The mechanisms of how FRQ inhibits its own transcription are the object of active research (12,14–16). Recent experiments indicate (16,17) that WC-1 is mainly located in the nucleus, whereas most of FRQ is found in the cytosol. Due to the low amount of nuclear FRQ (FRQ_n) in comparison with WC-1, it was suggested that FRQ could not inhibit the WCC by complex formation. Instead, FRQ was proposed to act more as a catalyst in a phosphorylation-dependent inactivation of WCC (13,16). In this article paper we describe and analyze a kinetic model for circadian oscillations in N. crassa under dark conditions. The model predicts that even at low levels, FRQ_n can inhibit frq transcription by binding to WCC with a 1:1 stoichiometry. The prerequisite for sustained oscillations is the removal of the FRQ_n:WCC complex from the system, for example by degradation. Our model is the first that highlights the importance of FRQ-dependent degradation of WCC (WC-1_n), which is under investigation. In the case when FRQ_n inhibits the WCC in a catalytic-like manner, oscillations only appear possible when FRQ_n is removed rapidly enough from the system.

THE MODEL

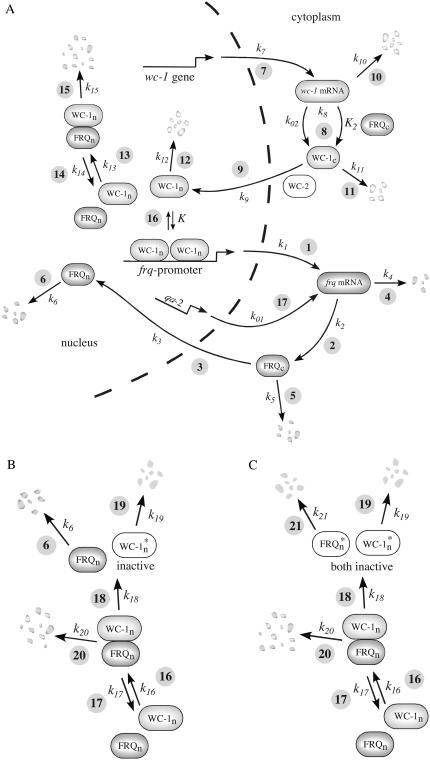
The model is shown in Fig. 1 A. Steps 1–6 represent the expression of frq, including transcription (step 1), translation (step 2), and translocation of FRQ protein into the nucleus (step 3), the degradation of frq mRNA (step 4), as well as degradation of cytosolic and nuclear FRQ (steps 5–6). We considered different rate constants for cytosolic and nuclear FRQ degradation to make minor adjustments in the period for the frq mutants. Because there is much less nuclear FRQ than cytoplasmic FRQ, and because the degradation rate constant of nuclear FRQ (k₆) is significantly lower than the cytosolic FRQ degradation rate constant (k₅), in the model the degradation of total FRQ is mostly determined by the cytosolic FRQ degradation. The cytosolic FRQ degradation rate constants are in good agreement with experimental estimates of total FRQ degradation (Table 1; see Ruoff et al. (31)). The results from the model remain similar even when k₅ and k₆ values are set equal to the experimental FRQ degradation rate constants but with slightly shorter periods and reduced amounts of FRQ. Steps 7–12 represent the expression of wc-1 and nuclear localization of WC-1 with degradation reactions (steps 10–12). WC-2 is present in excess over WC-1 and the concentration of WC-2 does not change during the circadian cycle (11,12). Therefore, we consider WC-2 as a constant and have not included WC-2 in the model. In addition, the WCC complex is represented by WC-1_n. Step 8 describes the FRQ promoted accumulation of WC-1. Several ways to represent step 8 have been investigated and will be discussed below. The step with rate constant k₀₂ represents a minor contribution to WC-1_c synthesis in the absence of FRQ (6,11,13). Steps 13–15 represent the inactivation of WC-1_n by binding to FRQ_n with a 1:1 stoichiometry and the subsequent degradation (or inactivation) of the formed complex. Step 16 represents the binding of WC-1_n at the frq promoter. The frq promoter contains two light responsive elements (LREs), where the distral element (“the clock (C)-box”) (18) appears necessary for rhythmicity (19). Each LRE contains two GATN sequence repeats, each probably capable of binding the Zn-finger domain from either WC-1 or WC-2. In its present form, the model suggests that at least two WC-1_n molecules need to bind to the promoter (C-box), because a reaction order <2 (with respect to [WC-1_n], see Eq. 1a) does not generate oscillations. With an increasing reaction order/Hill coefficient, ≥2 oscillations are more easily generated with a larger oscillatory domain, which was also observed in other studies; see for example Yu et al. (20). The binding of WC-1_n to the frq promoter is described as a rapid equilibrium with dissociation constant K leading to Eq. 1a in the frq transcription rate; for derivation see Appendix. The rate equations of the model are:

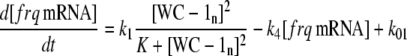(1a)

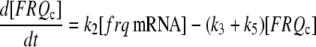(1b)

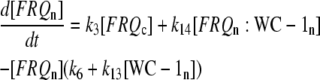(1c)

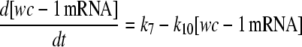(1d)

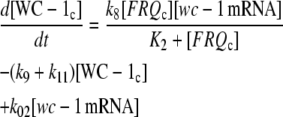(1e)

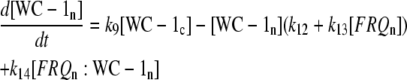(1f)

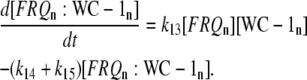(1g)

FIGURE 1.

Model of the Neurospora clock containing different interactions between nuclear FRQ and nuclear WC-1 (representing the WCC). (A) Model with FRQ_n:WC-1_n formation and degradation. This model is described by Eqs. 1a–g. The concentration of WC-2 is constant and not included in the equations. For discussion, see main text and the Appendix. (B) Model where FRQ_n inhibits WC-1_n by a “catalytic-like” interaction. (C) Model leading to inactive WC-1_n* and FRQ_n*. This model is kinetically equivalent to that shown in Fig. 1 A.

TABLE 1.

Rate constants (25°C) and activation energies

	frq+	Frq1	Frq7	frqS513I
k3, h−1	0.05	0.15	0.05	0.05
k5, h−1 (31)*	0.27	0.4	0.15	0.1
K6, h−1	0.07	0.1	0.01	0.006

Other rate constants (frq mutant independent; experimental rate constants are indicated by an asterisk followed by a reference): k₁ = 1.8 a.u. h⁻¹; k₂ = 1.8 a.u. h⁻¹; *k₄ = 0.23 h⁻¹ (29); k₇ = 0.16 a.u. h⁻¹; k₈ = 0.8 a.u. h⁻¹; k₉ = 40.0 a.u. h⁻¹; *k₁₀ = 0.1 h⁻¹ (20); k₁₁ = 0.05 h⁻¹; k₁₂ = 0.02 h⁻¹; k₁₃ = 50.0 a.u. h⁻¹; k₁₄ = 1.0 h⁻¹; k₁₅ = 5.0 h⁻¹; K = 1 .25 a.u (describing frq⁺); K = 8.5 a.u (describing ER24); K₂ = 1.0 a.u.; a.u. = arbitrary units.

Activation energies (kJ/mol) for the temperature description of frq⁺ and ER24: E₁ = 62.6; E₂ = 20.9; E₃ = 25.4; E₄ = 15.2; E₅, curved Arrhenius equation, see Figs. S4 (Supplementary Material); E₆ = 31.9; E₇ = 104; E₈ = 22.0; E₉ = 66.2; E₁₀ = 30.0; E₁₁ = 50.6; E₁₂ = 25.4; E₁₃ = 58.6; E₁₄ = 50.2; E₁₅ = 50.4; E_K, curved Arrhenius equation, see Fig. S4 (Supplementary Material); 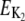= 68.8.

Concentrations in arbitrary units (a.u.) reflect the number of molecules/moles per cell/septum department. Table 1 shows the rate constants and activation energies for the modeled frq alleles and the ER24 mutant. Experimentally determined rate constants are indicated in Table 1 by an asterisk together with respective references. The other rate constants have been chosen to fit the model to experimental observations such as phase relationships among different components and various mutant behaviors. Fig. 1, B and C, show alternative possibilities for how WC-1_n inactivation can occur, which are discussed later in this article. The rate equations for these additional inhibition mechanisms are given in the Supplementary Material.

Computational methods

The differential equations were solved numerically and analyzed by using the FORTRAN subroutine LSODE (21) and XPPAUT (22). Ode-files, FORTRAN code, and a MATLAB (The MathWorks, Natick, MA, www.mathworks.com) version of the model are available.

RESULTS

Modeling frq⁺ behavior

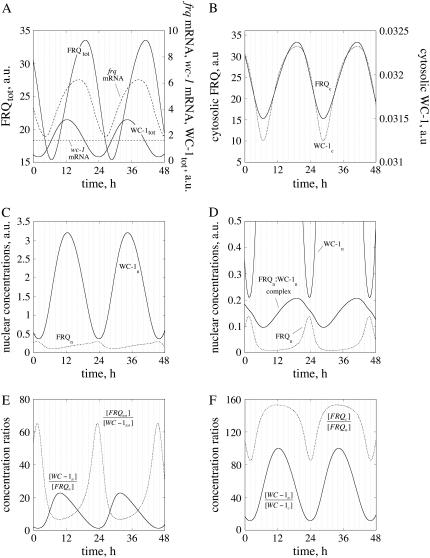
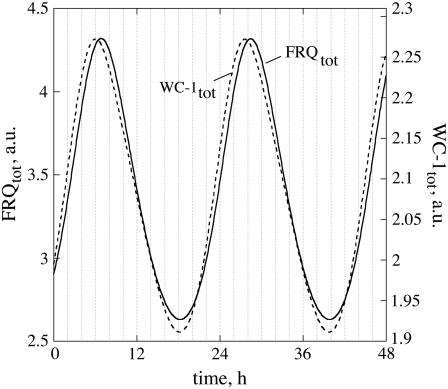
Fig. 2 shows the oscillations for the frq⁺ parameterization. In Fig. 2 A, total (nuclear and cytosolic) amounts of WC-1 and FRQ are shown along with their respective mRNAs. As seen from Eq. 1d, no transcriptional regulation of wc-1 mRNA is considered, leading to a constant wc-1 mRNA level as observed experimentally (6). Total FRQ and WC-1 oscillations have, as observed experimentally (6), a phase difference of ∼7 h (Fig. 2 A). As shown by experiments (12,14,16), total FRQ levels are comparable or higher than total WC-1 levels (Fig. 2 A), but this situation is reversed in the nucleus where most of the WC-1 is located (16) (Fig. 2 C). The reaction rates (time derivative of concentration) in total FRQ and WC-1 levels are predicted to show an “inverse variation relationship”, i.e., whenever the velocity of total FRQ production (or consumption) is at a maximum, the rate of total WC-1 is at a minimum and vice versa (Fig. 2 A, Fig. S1 (Supplementary Material)). A similar “inverse” phase relationship can be seen between sinus and cosinus functions, as for example in a harmonic oscillator. The apparent reason for this, using a rough description, is that the FRQ production rate is dependent on the concentration of the transcription factor WC-1 (mediated via the frq-mRNA), whereas FRQ negatively affects the WC-1 reaction rate by removing it. An implication of this inverse relationship is given in the Discussion.

FIGURE 2.

Oscillation profiles for frq⁺ parameterization. (A) Oscillations in frq and wc-1 mRNA, and in total FRQ and WC-1 levels. (B) In-phase oscillations of cytosolic FRQ and WC-1 proteins. (C) Anti-phase oscillations of nuclear FRQ and WC-1 proteins. (D) Same oscillations as in C, but including the oscillatory complex formation between nuclear FRQ and WC-1. (E) Oscillations in the ratios between nuclear WC-1/FRQ levels and total FRQ/WC-1 levels, respectively. (F) Oscillations in the ratio between nuclear and cytosolic WC-1 levels and nuclear and cytosolic FRQ levels.

Fig. 2 D shows the oscillations of the FRQ_n:WC-1_n complex in comparison with nuclear (unbound) WC-1 and FRQ (see also Fig. 2 C). This low amount of the FRQ_n:WC-1_n complex is consistent with experimental observations (12,16,17). Fig. 2, E and F, show oscillatory concentration ratios between WC-1_n and FRQ_n, FRQ_tot and WC-1_tot, and between the nuclear and cytosolic forms of WC-1 and FRQ. The model indicates that all ratios vary significantly during the circadian cycle, because the phases of FRQ and WC-1 are quite different.

Variable expression of frq and wc-1

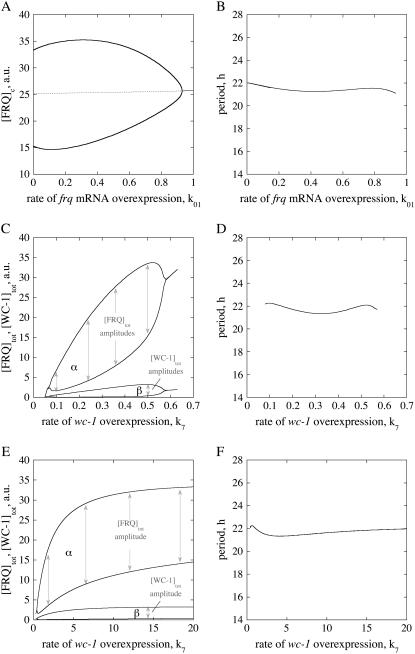
Aronson et al. (23) overexpressed frq by using a quinic acid (QA) inducible system [frq⁺(qa-2pFRQ)] in a wild-type background. Only small variations in the period length were observed at low QA concentrations, whereas rhythmicity was lost at higher concentrations. The same experiment can be simulated using the model by including an additional transcription of frq (process 17, Fig. 1 A) with rate constant k₀₁. As observed in the experiment (23), increasing k₀₁ values show little changes in the period length, which is rather unexpected considering that the period of a limit cycle oscillator is generally affected by parameter changes. However, oscillations stop when k₀₁ becomes too large (Fig. 3, A and B), because the system crosses a Hopf bifurcation (24) and enters into a region of a steady state.

FIGURE 3.

Overexpression of frq and wc-1. (A) One-parameter bifurcation diagram of cytosolic FRQ levels as a function of k₀₁. Dashed and solid lines denote the unstable and stable steady states, respectively. (B) Period length as a function of k₀₁, simulating the rate of frq⁺ (qa-2pFRQ) overexpression in a frq⁺ genetic background. (C) Diagram showing total FRQ and WC-1 levels/amplitudes as a function of wc-1 transcription rate k₇. (D) Period length as a function of k₇. (E) FRQ_tot and WC-1_tot amplitudes show saturation behavior in wc-1 overexpression when using Eq. 1e″. (F) Period length as a function of k₇ when Eq. 1e″ is used.

Cheng et al. (11) overexpressed wc-1 in a wc-1⁻, qa-WC-1 strain. Whereas at low QA concentrations no oscillations were found, rhythmicity was observed at higher QA levels where increased wc-1 transcription rates show increased amplitudes of WC-1 and FRQ. As found experimentally (16), the amplitude of total FRQ oscillations in the model is higher than the amplitude for total WC-1 (Fig. 2 A), but, as observed by Cheng et al. (11), and as seen in Fig. 3 C, both amplitudes increase up to a certain level when wc-1 expression (k₇) is increased. The period is little affected (Fig. 3 D, Fig. S2 (Supplementary Material)).

It may be noted that very similar behavior to that shown in Fig. 3, C and D, can also be observed (data not shown) when the accumulation rate in WC-1_c (Eq. 1e) is made independent of FRQ_c and is only first-order with respect to wc-1 mRNA, i.e., when Eq. 1e is written in the form:

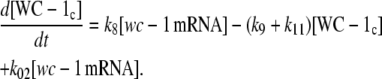(1e′)

Another possibility is that d[WC-1_c]/dt shows saturation kinetics with respect to wc-1 mRNA and FRQ_c, where Eq. 1e takes the form:

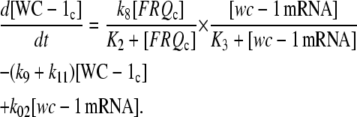(1e″)

In the case of Eq. 1e″, FRQ_tot and WC-1_tot amplitudes (Fig. 3 E) and the period length (Fig. 3 F) show saturation behavior and become independent of the magnitude of wc-1 overexpression (k₇), which improves the robustness of the model. A mechanism of how saturation kinetics in FRQ_c and wc-1 mRNA may occur without saturating protein synthesis kinetics with respect to the ribosomes is discussed below.

Lee et al. (6) applied a 4 h QA pulse in a frq¹⁰:qa-2FRQ strain and observed that FRQ peaked before WC-1 by ∼8–12 h. The model shows the same dynamic behavior as observed in the experiment (Fig. S3, Supplementary Material).

Modeling ER24 mutant behavior

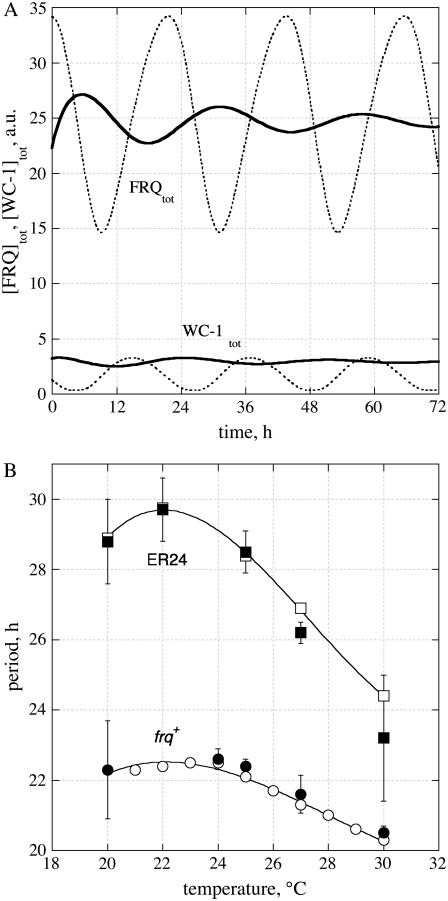
A sufficiently strong binding of WC-1 at the frq promoter is needed to get sustained oscillations. Weakening the binding of WC-1 to the frq promoter by increasing the dissociation constant K (Fig. 1 A, Eq. 1a) leads to an increased period and eventually to damped oscillations (solid lines in Fig. 4 A). A very similar behavior is observed for the mutant ER24. ER24 has an L to I point mutation at a conserved position in the Zn finger DNA-binding domain of WC-2 (25). Thus, the model suggests that ER24 may have a weaker binding of WCC (represented by WC-1_n) to the frq promoter.

FIGURE 4.

Modeling ER24 behavior. (A) Oscillations at 25°C describing ER24 behavior (solid lines) when K is increased from 1.25 a.u. (frq⁺ value) to 8.5 a.u. Dotted lines show the frq⁺ oscillations. (B) Comparison between experimental (solid symbols) and simulations (open symbols) of temperature behavior for ER24 (squares) and frq⁺ (circles).

An interesting aspect of ER24 is its partial loss in temperature compensation with period variations between 23 and 30 h and a period maximum at ∼22°C (Fig. 4 B). frq⁺ shows a similar maximum, but due to its temperature compensation, the period length varies only between 20 h and 22 h (Fig. 4 B). We wondered how the model would “explain” the concave experimental period-temperature relationship for frq⁺ and ER24. Starting with ER24, the model suggests that the dissociation constant K is relatively large and increases with increasing temperature (i.e., from 3 to 11 a.u. between 20° and 30°C; Fig. S4A, Supplementary Material), but with a lower activation energy at 30°C compared to 20°C (Fig. S4B, Supplementary Material). For frq⁺, the behavior is qualitatively similar, with a strong WC-1_n binding at 20°C (K ≈ 10⁻³ a.u.), which weakens for higher temperatures (>24°C) with K values between 1 a.u. and 2 a.u. (Figs. S4C and S4D, Supplementary Material). In addition to these observations, k₅ needs to increase with increasing temperature, but with a curved Arrhenius-plot with apparent activation energies of ∼25 kJ/mol for the range 20–25°C and 6 kJ/mol for the range 25–30°C (Figs. S4E and S4F, Supplementary Material).

Modeling frq mutants

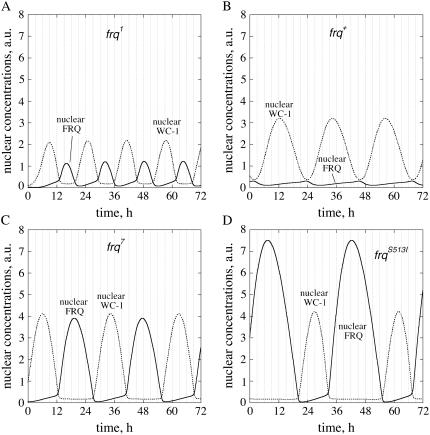
Several point mutations in frq show altered period lengths (26,27). Calculations (28,29) as well as experiments (30,31) indicate that a high stability of FRQ (slow FRQ degradation such as in frq⁷ and frq^S513I) leads to large period lengths, whereas a low stability in FRQ (rapid FRQ degradation, such as in frq¹) leads to short periods. The period lengths of frq¹, frq⁷, and frq^S513I can be modeled using the rate constants shown in Table 1, where the cytosolic FRQ degradation rate constants are in good agreement with experimental estimates (31). For frq¹, a somewhat larger FRQ¹ translocation into the nucleus had to be assumed to obtain stable oscillations with a period of 16 h. This could be related to the fact that the mutation in frq¹ is close to the nuclear localization sequence of FRQ (26). The model predicts that total FRQ levels are always higher than total WC-1 levels and that FRQ_tot oscillations are larger in amplitude than WC-1_tot oscillations, especially for the long-period mutants, which have a higher FRQ protein stability (Fig. S5, Supplementary Material). Nuclear FRQ (FRQ_n) levels are predicted to increase relative to nuclear WC-1 levels with increasing FRQ stability and period (Fig. 5). Whereas in frq¹ and frq⁺ nuclear FRQ levels are lower than nuclear WC-1 levels (Fig. 5, A and B), FRQ_n and WC-1_n concentrations are approximately equal in frq⁷ (Fig. 5 C). In frq^S513I, the model predicts that nuclear FRQ levels should be significantly larger than WC-1_n levels (Fig. 5 D).

FIGURE 5.

Nuclear FRQ levels (solid lines) and nuclear WC-1 levels (dotted lines) in parameterizations of (A) frq¹, (B) frq⁺, (C) frq⁷, and (D) frq^S513I, respectively.

DISCUSSION

Oscillatory behavior

We focus on frq⁺ oscillatory behavior because most experiments on relative component concentrations, their amplitudes, and phase relationships have been reported for frq⁺. As observed experimentally (12,14,16), the model shows total FRQ levels that are generally larger than total WC-1 levels, whereas nuclear FRQ levels are significantly lower than nuclear WC-1 (Fig. 2 A). The amplitude of total FRQ can be characterized as the ratio between maximum and minimum levels of total FRQ. With the parameter set presented here, this ratio is ∼2.3, but increases with increasing wc-1 transcription rates as shown in Fig. 3 C. An analysis of published experimental FRQ oscillations shows a considerable variation in this ratio, ranging from ∼1.6 to 5 (6,11,32,33). Also the shape (more pulsatile versus more smooth behavior) of the frq-mRNA and FRQ oscillations shows considerable variations between experiments. The reason for this variability may have multiple reasons, for example reflecting different types and properties of FRQ antibodies, age of culture, as well as slightly different light or nutritional conditions. As implicitly indicated by the study of Cheng et al. (11), the variability in FRQ amplitude may perhaps also be due to environmental variations in the wc-1 transcription rate.

The observation that FRQ_n is significantly lower than WC-1_n levels led to the suggestion (16) that nuclear FRQ may not to be capable of controlling frq transcription by binding to the much more abundant WC-1_n. However, the calculations presented here clearly show that even low levels of FRQ_n enable rhythmic frq transcription by binding to WC-1_n. The model simulates that the FRQ_n:WC-1_n complex is present at low concentrations (as found experimentally (16)).

It was recently suggested that FRQ_n may promote, in a “catalyst-like” manner, the deactivation of WCC by phosphorylation (13,16). We have investigated this possibility using the scheme shown in Fig. 1 B, where FRQ_n interacts with WCC (WC-1_n) and inactivates it by reaction 19. This mechanism was not able to generate oscillations within a 24 h period regime without removing the FRQ_n:WC-1_n complex (Fig. 1 B, reaction 20) and without a significant removal of FRQ_n (reaction 6). However, even when oscillations within the circadian period regime were obtained by allowing FRQ_n and FRQ_n:WC-1_n removal, the calculated phase difference between FRQ_tot and WC-1_tot was too small compared with the experimental (6) and calculated results (Fig. 6). This indicates that the removal of the FRQ_n:WC-1_n complex appears essential to obtain correctly phased FRQ and WC-1 oscillations, and that a significant amount of FRQ and WC-1 are removed through the FRQ_n:WC-1_n complex. The mechanism shown in Fig. 1 C is kinetically equivalent to the FRQ_n:WC-1_n degradation mechanism of Fig. 1 A, leading to “inactive” FRQ_n* and WC-1_n* proteins, which, in principle, may still be detectable by Western blotting. Thus, Western analysis may not be able to distinguish unequivocally between degradation and inhibition mechanisms. A recent model study of the Neurospora clock (20) independently indicated that inactivation of WC-1_n by binding between FRQ and WC-1_n is more effective than a catalytic inactivation of WC-1_n by FRQ.

FIGURE 6.

Obtained oscillations with a period of 21.6 h using the scheme of Fig. 1 B (k₁₃ = k₁₄ = k₁₅ = 0) with k₆ = 1.2 h⁻¹, k₁₆ = 50.0 a.u. h⁻¹, k₁₇ = 0, k₁₈ = 1.0 a.u. h⁻¹, k₁₉ = 1.0 a.u. h⁻¹, and k₂₀ = 3.0 × 10⁻² a.u. h⁻¹. Note the small difference in phase between FRQ_tot and WC-1_tot compared to Fig. 2 A and experimental values (6). To get oscillations with a circadian period when using this scheme, the k₆ value needs to be unrealistically high (1.2 h⁻¹) in comparison with experimental results (30–32).

Our model's simulation that wc-1 mRNA levels do not need to be oscillatory and that the amplitude of WC-1_tot is lower than for FRQ_tot (Fig. 1 A) is in agreement with experimental findings ((6,34). Furthermore, reaction rates in FRQ_tot and WC-1_tot show an “inverse” relationship: whenever the (synthesis or degradation) rate in FRQ_tot is highest, WC-1_tot levels and WC-1_tot synthesis/consumption rates are approximately constant (Fig. 1 A, Fig. S1 (Supplementary Material)). For example, during the decay phase of FRQ_tot, the model predicts that WC-1_tot levels remain approximately constant, a behavior that has also been observed experimentally (see Fig. 3 B in Schafmeier et al. (13)).

Overexpressing frq with the inducible qa-2 promoter in a frq⁺ genetic background shows, in agreement with experiments (23), oscillations with little variation in period (Fig. 3 A). When the rate of frq overexpression becomes too high, the oscillations stop (crossing a Hopf bifurcation) and the system enters a stable steady-state region (Fig. 3 B).

When wc-1 is overexpressed, the amplitude in total FRQ levels increases with increasing wc-1 transcription (k₇) rates (Fig. 3, C and E), whereas only small variations in the period lengths are observed (Fig. 3, D and F), a behavior that is also found experimentally (11). It is not established (11) whether the Neurospora rhythm can show saturation kinetics when wc-1 is overexpressed as shown in Fig. 3 E. However, we wish to point out that robust oscillations showing saturation kinetics in period and amplitudes with respect to wc-1 overexpression (and without saturating the ribosomes) may occur due to a FRQ-promoted expression of WC-1_c. When the rate of translation is (for the sake of simplicity) first-order with respect to an association between wc-1 mRNA and FRQ_c, then it can be shown (see Appendix) that overexpression of wc-1 (increase of k₇) shows saturation kinetics. In this respect, the FRQ-promoted synthesis of WC-1_c may be a mechanism leading to robust oscillations. The above mechanism is supported by experimental results showing that the FRQ-promoted accumulation of WC-1 needs the presence of WC-2 (13) and that FRQ interacts with WC-2 (12). The reaction sequences 8 and 9 (Fig. 1 A) may also be viewed as a FRQ-promoted assembly of WCC as suggested by Schafmeier et al. (13). In summary, and as seen in Fig. 3, C and E, the model shows (in agreement with experiments (6,11,13)), that FRQ_tot oscillations have larger amplitudes than WC-1_tot oscillations.

In agreement with experimental results (28,31), the frq mutants are characterized by different FRQ stabilities (Table 1); i.e., in the short-period mutant frq¹, FRQ is more rapidly degraded than in frq⁺, whereas in the long-period alleles (frq⁷, frq^S513I) FRQ is more stable than in frq⁺ and the FRQ amplitude increases with increasing FRQ stability (Fig. 5, Fig. S2 (Supplementary Material)). In frq¹, FRQ_n is somewhat higher than in frq⁺ (Fig. 5), which is due to the increased import (larger k₃) of FRQ¹ into the nucleus (Table 1).

WC-1 binding to frq promoter and temperature compensation

The model predicts that with a decreasing binding strength of WC-1_n (WCC) to the frq promoter, the period increases and oscillations become damped and stop if the dissociation constant K becomes too large (Fig. 4 A), similar to what was observed in ER24 (25). This suggests that in ER24, the binding of WC-1_n to the frq promoter should be weaker than in frq⁺, especially at low temperatures.

An interesting aspect is that when the binding between WC-1_n and the frq promoter weakens (described by increased K values) with increasing temperature, the oscillator can show partial temperature overcompensation at low temperatures as found experimentally. Recently, Daniel Forger from the University of Michigan made the interesting observation that the Goodwin oscillator (35,36) cannot be temperature compensated when its inhibition term K is set to zero (D. Forger, University of Michigan, personal communication, 2006). Because K in the Goodwin oscillator and in the our model reflects a dissociation constant, the model's behavior described in Fig. 4 C and the observation by Forger indicate that binding of the transcription factor to the clock protein promoter is part of the temperature compensation mechanism in Neurospora crassa and possibly also in other organisms. Clock protein degradation and binding properties at clock protein promoters are some of the processes that are expected to lead to temperature compensation. It will be interesting to see what other processes will be found in the temperature compensation mechanism.

In our model, the temperature dependence for most rate constants is described by a single Arrhenius equation (Table 1). However, to get a close description of the experimental period-temperature profiles for of frq⁺ and ER24, a curved Arrhenius plot had to be employed for K and k₅. For k₅, the activation energy values used in the calculations are close to those estimated previously for the range 20–25°C (31), but a significant lower value had to be used (≈ 6 kJ/mol) for the range 25–30°C, where currently no experimental estimate exists. The need for curved Arrhenius plots in describing the temperature dependencies of k₅ and K is not unexpected, because FRQ degradation through the proteasome (37) and the binding of transcription factors to a promoter (38) are complex processes involving a variety of enzymes, proteins, and reaction steps. For example, enzyme- and ribozyme-catalyzed processes (39–42) can show curved or discontinuous Arrhenius plots similar to those shown in Fig. S4 (Supplementary Material). The origin of these curved Arrhenius plots may be related to temperature-induced conformational changes of an enzyme or ribozyme (40) or may already be inherent in the kinetics (40).

Researchers are beginning to unravel the mechanisms contributing to temperature compensation. A balance equation (43) was recently formulated, which is closely related to the concept of opposing reactions made by Hastings and Sweeney in 1957 (44). The balance equation has been able to account for temperature compensation in several chemical (43,45–50) and circadian oscillators (31,36,51–54) and was also applied to steady-state kinetics (55). Our study indicates that the activation energies participating in the balance equation may not necessarily be independent of temperature (as described above) but may result in “dynamic temperature compensation” (55) when lumping complex biochemical processes (elementary reactions) into one reaction step. A more detailed analysis of such behavior is being considered elsewhere. There are several other descriptions on how to explain temperature compensation, and the reader is referred to these articles (44,56–61) and references therein.

Comparisons with other models

A variety of models have been put forward to understand the mechanism of the Neurospora circadian oscillator focusing on aspects such as single negative feedback loops (36,62–65), interlocking positive and negative feedback loops (20,66,67), delay kinetics (67,68), or the explicit inclusion of the transcription factors WC-1/WCC (20,64,65). The models by Yu et al. (20), Smolen et al. (69), and the (two-loop) models by Francois (67) have included inhibition of WCC by binding of FRQ to WCC with a subsequent degradation of the FRQ-WCC complex. In these models, total FRQ and WCC show anti-phase oscillations as observed in Fig. 2 C. Because we were interested whether small amounts of nuclear FRQ would allow the inhibition of WC-1 and lead to realistic oscillatory behavior, our model differs from those of Yu et al. (20), Smolen et al. (69) and Francois (67) by considering explicitly nuclear and cytosolic FRQ and WC-1 levels. In doing so, our model predicts significant phase differences when comparing nuclear FRQ and WC-1 levels (Fig. 2, C and D) with cytosolic FRQ and WC-1 levels (Fig. 2 B). We are also able to describe experimental behavior when overexpressing frq and wc-1 (Fig. 3), and suggest the importance of WC-1_n (WCC) binding to the frq promoter as part of Neurospora's temperature compensation mechanism (Fig. 4).

SUMMARY

Our model suggests that small amounts of FRQ_n are capable of inhibiting frq transcription by binding to WC-1_n (representing WCC) as long as FRQ_n is rapidly degraded or otherwise removed or inactivated together with the interacting WC-1_n. The formed complex between WC-1_n and FRQ_n is present at low oscillatory concentrations compared with WC-1_n. For frq⁺, the model is in qualitative agreement with experimental nuclear and cytosolic FRQ and WC-1 levels and their phase relationships and can account for the increase of FRQ amplitude when wc-1 is overexpressed. The model also accounts for the loss of rhythmicity above a certain level of frq overexpression. The model predicts that FRQ levels increase in frq mutants in the order frq¹ < frq⁺< frq⁷ < frq^S513I, whereas WC-1 amplitudes in these mutants remain more or less unaffected. The ER24 phenotype can be explained by a weaker WC-1_n (WCC) binding to the frq promoter. The observed temperature overcompensation in ER24 and frq⁺ can be modeled by an increase of the WC-1_n dissociation from the frq promoter with increasing temperatures. The model suggests that the WC-1_n (WCC) binding to the frq promoter is part of Neurospora's mechanism for temperature compensation.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

APPENDIX

Calculating the rate of frq transcription

The frq promoter region contains two binding regions for WCC (19), one of which (the clock box or C-box) (18) is required for rhythmicity. The C-box in turn contains two imperfect distinct repeats of a 15 basepair consensus sequence, suggesting that WCC (WC-1_n) binding may occur at two sites. In the following, we use WC-1_n to denote nuclear WCC concentrations:

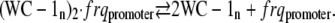(A1)

Assuming that reaction A1 is in a rapid equilibrium, the equilibrium (i.e., dissociation) constant of reaction A1 is given by:

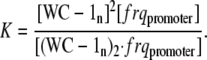(A2)

The rate of frq transcription v is given by Eq. A3:

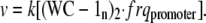(A3)

In the model, we assume that the total amount of frq promoter regions [frq_promoter]_tot is constant, i.e.,

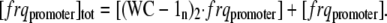(A4)

From Eq. A2, an expression for [frq_promoter] can be found and inserted into Eq. A4, giving

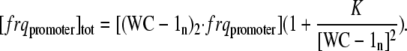(A5)

Solving Eq. A5 for [(WC-1_n)₂ · frq_promoter] and inserting it into Eq. A3, leads to the final expression for the rate of frq transcription v:

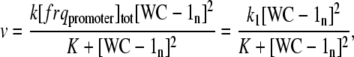(A6)

with k₁ = k [ frq_promoter]_tot.

Possible saturation kinetics of wc-1 overexpression

Because FRQ_c and WC-2 are necessary for the expression of WC-1_c (13) and because FRQ and WC-2 interact with each other, we consider that FRQ_c is associated with WC-2. To show saturation behavior in period length and amplitudes when wc-1 is overexpressed, an interaction between FRQ_c:WC-2 and the translation machinery or wc-1 mRNA appears necessary. We consider here the interactions between FRQ_c:WC-2 and wc-1 mRNA, which is assumed to be in rapid equilibrium with the complex FRQ_c:WC-2:wc-1 mRNA that leads to the translation of wc-1 mRNA and to a FRQ-assisted formation of WC-1_c:WC-2, i.e.,

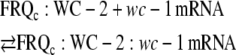(A7)

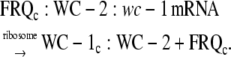(A8)

The WC-1_c:WC-2 complex is then transported into the nucleus (Fig. 1 A).

Because we have not explicitly considered WC-2 in the model equations (the WC-2 concentration is approximately constant and in excess over WC-1 (11)), we do not include WC-2 in the following mass balance equations. If, for a given circadian time,

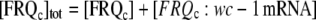(A9)

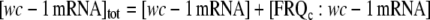(A10)

denote total concentrations of FRQ_c and wc-1 mRNA and c₀ = [FRQ_c] _tot + [wc-1 mRNA]_tot, then we can write

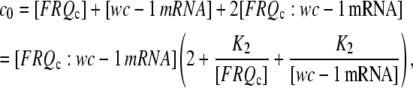(A11)

where K₂ is the rapid equilibrium constant between FRQ_c:wc-1 mRNA, and FRQ_c, wc-1 mRNA, given by

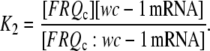(A12)

Because the rate of wc-1 translation (v_tr) is assumed to be proportional to [FRQ_c:wc-1 mRNA], v_tr is proportional to 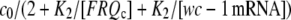showing saturation behavior both in FRQ_c or wc-1 mRNA. As a result, whenever wc-1 mRNA is overexpressed, its translation rate v_tr is limited by the amount of FRQ_c.