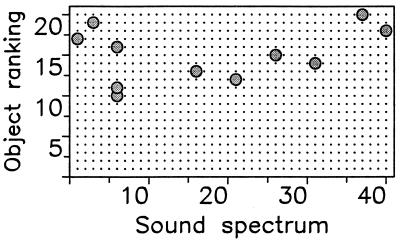
Figure 2.

Evolution of protolanguage in the context of misunderstanding. There are 20 objects and 40 sounds, but evolution leads to a language that uses only 9 sounds to describe 11 objects. Sounds are represented on a linear spectrum by numbers between 0 and 1. The similarity between two sounds, x_i and x_j, is given by s_ij = exp(−α|x_i − x_j|). For the computer simulation, m sounds are randomly chosen from a uniform distribution on (0,1). Objects have different values, a_i, chosen from a uniform distribution on (0,1). The payoff for language L against L′ is given by Eq. 2. In this simulation, we do not model individual players but simply evaluate whether or not a mutant language will be able to invade and replace the existing language. The simulation is started with a language L whose active matrix P has random elements p_ij sampled from a uniform distribution on (0,1) and normalized such that all rows have a sum of one. The passive matrix Q is derived from the active matrix: q_ji = p_ij/Σ_ip_ij. Then a mutant language L′ is produced. If F(L′,L) < F(L,L), then L′ cannot invade. Another mutant is generated. If F(L′,L′) > F(L′,L) > F(L,L), then L′ can invade and take over. The original language L is replaced by L′. The simulation searches for mutants that can replace L′. (It is also possible, though very rare, that F(L′,L) > F(L,L), but F(L′,L′) < F(L,L′). In this case, there would be a stable equilibrium between L and L′ and the simulation would stop.) The figure shows the final outcome after 100,000 different mutants, but the basic structure of the language is already present after 4,000 mutants. The x axis indicates the different sounds sorted according to their x_i value; the y axis indicates objects ranked according to their a_i value (20 being the most valuable). The 11 most valuable objects (y axis) are associated with nine different sounds (x axis). One sound is used for three different objects (including the two least valuable objects described by the language). The sounds seem ideally selected to minimize their similarity. Parameter values: α = 2, n = 20, m = 40; mutation process: all p_ij values between 0 and 1 are randomly changed within an interval ± 0.01; with probability 0.001, any p_ij is changed to 0 or 1; with probability 0.001, a whole column or a whole row of the P matrix is changed into 0. The mutation rules are designed to provide enough chance to gain or lose sounds or objects.