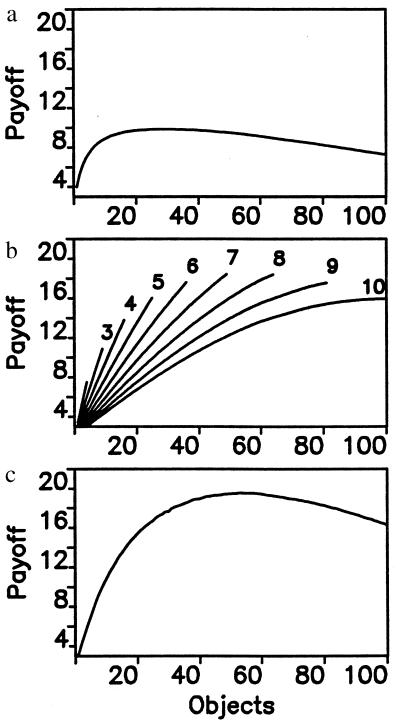
Figure 3.

Word formation can overcome the error limit. Suppose there are n = 100 objects with values a_i uniformly distributed between 0 and 1. (a) Without word formation, each object is described by one sound. The similarity between different sounds is ɛ. The maximum payoff of a language with m sounds is given by F = [1 + (m − 1)ɛ]⁻¹Σ_i=1^ma_i, where the a_i are ranked in descending order. In our example, ɛ = 0.2. The maximum payoff is obtained if the 28 most valuable objects are being described by individual sounds. All other objects are ignored. (b) As a simple example of word formation, we consider that each word consists of two sounds. The maximum payoff of a language with m sounds is F = [1 + (m − 1)ɛ]⁻²Σ_i=1^Ma_i, where M is the smaller of m² or n. In this model, correct identification of a word requires correct understanding of each individual sound. The figure shows the payoff curves for languages that have m = 2 to 10 different sounds. For each language, it is best to make use of the whole repertoire, that is, to use all m² combinations as words. The maximum payoff is achieved for m = 7, which leads to 49 words describing 49 objects. (c) A more sophisticated theory of word recognition assumes that correct understanding of a word is based on matching the perceived sequence of sounds to all combinations that are thought to be part of the lexicon of the language. For our example, we find that the maximum fitness is obtained for m = 11 sounds, when 52 of the 121 possible combinations are used as words. A smaller or higher number of sounds, m, leads to a lower maximum fitness. If longer words are being admitted, then both cases (b and c) lead to optimum solutions that describe a larger fraction of all objects.