Mapping Quantitative Trait Loci Affecting Susceptibility to Marek's Disease Virus in a Backcross Population of Layer Chickens

Abstract

Marek's disease (MD), caused by the oncogenic MD avian herpes virus (MDV), is a major source of economic losses to the poultry industry. A reciprocal backcross (BC) population (total 2052 individuals) was generated by crossing two partially inbred commercial Leghorn layer lines known to differ in MDV resistance, measured as survival time after challenge with a (vv+) MDV. QTL affecting resistance were identified by selective DNA pooling using a panel of 198 microsatellite markers covering two-thirds of the chicken genome. Data for each BC were analyzed separately, and as a combined data set. Markers showing significant association with resistance generally appeared in blocks of two or three, separated by blocks of nonsignificant markers. Defined this way, 15 chromosomal regions (QTLR) affecting MDV resistance, distributed among 10 chromosomes (GGA 1, 2, 3, 4, 5, 7, 8, 9, 15, and Z), were identified. The identified QTLR include one gene and three QTL associated with resistance in previous studies of other lines, and three additional QTL associated with resistance in previous studies of the present lines. These QTL could be used in marker-assisted selection (MAS) programs for MDV resistance and as a platform for high-resolution mapping and positional cloning of the resistance genes.

MAREK'S disease (MD) of chickens is caused by the oncogenic MD avian herpes virus (MDV). When originally described in 1907 MD manifested as a mild endemic paralytic disease. MD today, however, is an acute highly contagious disease causing tumors in multiple visceral organs (Nair 2005) and is a major source of economic losses to the poultry industry (Morrow and Fehler 2004). The disease is well controlled by vaccination with the highly effective “Rispens” vaccine, but ever more virulent strains are constantly evolving and have already “broken” three vaccines (Nair 2005). There is thus great importance to developing methods of control based on well-documented genetic resistance to MDV (reviewed in Bumstead and Kaufman 2004).

Current genetic methods for improving resistance to MDV are based on family selection, which is expensive in terms of time, facilities, and selection space and poses the ethical dilemma of challenging large numbers of birds with a virulent pathogen. Identification of quantitative trait loci (QTL) for MDV resistance will allow marker-assisted selection (MAS) on an individual bird level, without need for routine challenge. This will greatly enhance efficacy of selection, reduce costs by orders of magnitude, and provide a platform for eventual identification of the quantitative trait genes (QTG) corresponding to the mapped QTL. QTL mapping can also provide information on epistatic interactions among the identified QTL, further increasing the potential for genetic improvement.

Polymorphic alleles at the MHC (B blood group) on chromosome 16 (reviewed in Weigend et al. 2001), the growth hormone gene (GH1) located on chromosome 1 (Kuhnlein et al. 1997; Liu et al. 2001), and the stem lymphocyte antigen 6 complex locus E (LY6E) located on chromosome 2 (Liu and Cheng 2003) have been shown to affect resistance to MDV. A series of QTL mapping studies for MDV resistance have been carried out under experimental challenge in crosses of two highly inbred White Leghorn lines, 6 and 7 (Avian Disease and Oncology Laboratory, ADOL), known to differ widely in susceptibility to MDV (Vallejo et al. 1998). Mapping in a backcross population of these lines identified a QTL for MDV resistance on chromosome 1 (Bumstead 1998); mapping in an F₂ cross of these lines identified QTL for MDV resistance on chromosomes 1, 2, 4, 7, and 8 (Vallejo et al. 1998; Yonash et al. 1999).

In this study, QTL affecting resistance to MDV were mapped by selective DNA pooling in a large reciprocal backcross (BC) population generated by crossing two partially inbred commercial Leghorn layer pure lines known to differ in resistance to this virus. One goal of this research was to determine if the QTL uncovered in the Leghorn lines investigated by Vallejo et al. (1998) and Yonash et al. (1999) were also a source of genetic variation in these commercial Leghorn lines.

MATERIALS AND METHODS

Resource population:

Stocks:

The experiment was carried out using facilities and two commercial Leghorn lines (henceforth, line 1 and line 2) of Hy-Line International (henceforth, Hy-Line). Both lines were partially inbred and fixed for alternative blood-type (BT) groups; B2/B2 in line 1 and B15/B15 in line 2. A previous screen of 102 microsatellite markers on these lines showed that 60 and 80% of the markers were fixed in line 1 and line 2, respectively. Both line 1 and line 2 have been subjected to selection for resistance to MD, and both are relatively resistant when compared to field strains. However, in experiments performed in 2000, 2003, and 2005 under the same challenge protocol as this study, absolute mortality of line 1 at the end of the test (19 w) was higher than that of line 2, by 41.4, 42.7, and 21.7%, respectively. Thus, under this challenge line 2 is distinctly more resistant than line 1. The 2003 test also included the F₆ generation of a cross of the two lines. This population exhibited a high level of mortality, with absolute mortality being 36.8% greater than that of line 2 and only 5.9% less than that of line 1 (J. A. Arthur, N. P. O'Sullivan, K. K. Kreager and Hy-Line, unpublished data).

Experimental populations:

To provide replication and some indication of QTL segregation within the two lines, each BC population was produced in five independent replicates, termed “families,” as follows. Five line-1 males were each pair mated with a single different line-2 female to produce an F₁ generation consisting of five independent full-sib F₁ families. A group of seven full-sib F₁ males from each of the five families were each pen mated to a group of 18–20 females from line 1 (total ∼35 males and 100 females) to produce a backcross population consisting of five independent families with line 1 as the recurrent parent (henceforth, BC-1), each family consisting of the progeny of seven full-sib F₁ males and 18–20 line-1 females. Six months later, the same five groups of F₁ males were each again pen mated to a group of 18–20 females from line 2 to produce the reciprocal backcross population (henceforth, BC-2), also consisting of five independent families. The BC-1 included 837 birds with 163–176 chicks per family; BC-2 included 1215 birds with 234–258 chicks per family. Two BT genotypes, B2/B2 and B2/B15 were present in BC-1, and two BT genotypes, B2/B15 and B15/B15 were present in BC-2.

MD challenge test:

Day-old BC-1 chicks were vaccinated with bivalent HVT/SB-1 vaccine (Merial Select, Gainesville, GA) and housed in brooder cages. This is the vaccine that was used prior to the current Rispens vaccine, and hence provides only partial protection to the chicks. At 7 days the chicks were inoculated subcutaneously with 500 PFU of the very virulent (vv+) strain (648A) of the MDV (Witter 1997) and then transferred to a floor facility challenge house. At 3 weeks of age, blood samples for blood typing and DNA isolation were collected and stored. Age at mortality was recorded on all chicks as an indicator of resistance to MDV until 116 days of age, at which time the test was terminated. This same procedure was repeated for BC-2 six months later, except that the test was terminated at 138 days of age. This test has been shown to result in data with substantial heritability (0.10–0.22) for sire progeny averages on the basis of 30 daughters (J. E. Fulton, P. Settar and Hy-Line, unpublished data).

DNA extraction and pool construction:

At 3 weeks of age, blood was collected from the jugular vein with 22-gauge needles in syringes containing EDTA. DNA was isolated from the blood using proteinase K digestion, salt, and ethanol precipitation (maniatis et al. 1982). The OD_260/280 ratios were subsequently determined. Each sample was diluted to ∼50 ng/μl DNA concentration, retested for DNA content, and further diluted to 25 ng/μl. Pools of DNA were made by combining equal volumes of the 25 ng/μl samples from each of the birds identified as belonging to the pool (see below).

To reduce the number of genotypings, selective DNA pooling (Darvasi and Soller 1994; Lipkin et al. 1998) was used. This method has proven very accurate in the Hy-Line laboratory (Lipkin et al. 2001). Because of the known effect of the MHC BT on MDV resistance, pools of DNA of resistant and susceptible birds were constructed within each BC × BT × family combination (CBF), as shown in Table 1. Progeny within each CBF combination were ranked by age at mortality, or designated as “survivors” if they survived until termination of the challenge test with no obvious symptoms of MD. The susceptible pools within each CBF combination consisted of the 20% of birds with earliest age to mortality. For all CBF combinations, the number of survivors was >20%. Hence, to match the number of birds in the susceptible pools, 21 (on average 20%) of the surviving birds were chosen at random for each family. This gave a total of 2 BC × 2 BT/BC × 5 families/BC–BT combination × 2 tails (resistant and susceptible)/CBF combination = 40 pools.

TABLE 1.

Pool composition according to backcross (BC), family (F), and blood type (BT)

				Proportion resistanta	No. per pool		Survival (days) in susceptible pool
BC	F	BT	Total no.			Resistant	Susceptible	Mean	Range
1	1	B2/B15	88	0.61	21	18	52.5	42–75
		B2/B2	75	0.56	20	15	56.0	42–72
	2	B2/B15	76	0.51	21	15	51.3	42–66
		B2/B2	87	0.53	21	17	60.6	40–90
	3	B2/B15	86	0.45	20	17	42.5	43–60
		B2/B2	90	0.47	20	18	54.2	42–63
	4	B2/B15	82	0.54	21	16	57.6	39–75
		B2/B2	87	0.49	21	17	57.6	31–76
	5	B2/B15	82	0.43	19	16	59.7	42–91
		B2/B2	84	0.43	20	17	55.6	41–72
2	1	B15/B15	110	0.71	21	22	62.9	49–77
		B2/B15	121	0.46	21	25	52.6	43–57
	2	B15/B15	119	0.76	21	20	60.2	49–72
		B2/B15	123	0.39	21	23	49.9	43–57
	3	B15/B15	121	0.66	21	23	61.8	42–77
		B2/B15	125	0.34	21	23	54.2	28–63
	4	B15/B15	123	0.63	21	23	57.4	42–70
		B2/B15	121	0.40	21	23	51.4	40–59
	5	B15/B15	125	0.66	21	22	60.2	45–74
		B2/B15	110	0.34	21	20	53.2	42–59

^aProportion surviving to the end of test, which was at 116 days for BC-1 and 138 days for BC-2.

Genotypic data:

Pools were genotyped for a total of 198 microsatellite markers chosen so that overlap in alleles between the two parent lines was absent or limited to a single allele. Since not all markers were informative for both backcrosses, 180 markers were used in BC-1, and 176 in BC-2; 158 markers were common to both BCs.

Marker locations were assigned according to the consensus 2000 chicken linkage map (http://iowa.thearkdb.org/). When there was a discrepancy between the consensus map and the chicken sequence (http://www.ensembl.org/Gallus_gallus/index.html), the order of the markers was based on the sequence. In these cases, as well as cases of markers that were not on the consensus map, additional markers flanking the questioned marker were identified that were in the same order in the sequence and the consensus map. The questioned marker was then positioned on the consensus map proportionally to these two markers. Linkage data derived from Hy-Line populations (Wang 2003) were available for chromosomes 4, 15, and Z, and these were used for analysis, since they gave a better fit to the sequence than did the linkage data of the consensus map. In addition, the study included five markers that were assigned to specific chromosomes but did not have specific locations and four markers that were not assigned to chromosomes.

Genome coverage:

The regions bracketed by the most proximal and the most distal markers on each of the 15 chromosomes tested with three markers or more, gave a total of 2180 cM. To this can be added on average 20 cM for each of these 15 chromosomes (total 300 cM) to account for chromosome coverage from the most proximal and the most distal markers to the chromosome ends, and another 20 cM for each of the remaining 10 chromosomes that were covered by only one or two markers (total 200 cM) to give total genome coverage of ∼2680 cM. Thus, approximately two-thirds of the 4000 cM chicken genome (Groenen et al 2000) was scanned in this study.

Genotyping methods:

For all markers, allele frequencies in the pools were estimated by densitometric PCR. Following Lipkin et al. (1998), frequencies estimated from pools were corrected for the overlapping shadow bands that are inherent in microsatellite markers and also for differential amplification between alleles when present.

Statistical methods:

The basis for all statistical tests of significance of marker–QTL linkage were the differences (D_hijk-values) in densitometric estimates of marker allele frequencies between the resistant and susceptible pools for the hth marker, ith backcross, jth blood-type, and kth family (MCBF)_hijk combination. All tests were carried out separately for the two backcrosses and for the combined data across the two backcrosses. Unless specified otherwise, the term “crosses” will refer to results of all three calculations (i.e., for BC-1, BC-2, and the combined data). The D_hijk were evaluated for significance using a variety of statistical tests (Z-test, chi square, interval analysis, ANOVA, and nonparametric sign test), each of which explored a somewhat different aspect of the data. In particular, the Z-test that was implemented (see details in the following) evaluates the main effect of a marker allele on D-values across CBF combinations. Thus, the Z-test is sensitive to main effects and provides an estimate of the direction of effect of specific alleles, but is insensitive to marker–blood-type–family interaction effects. The chi-square test analyzes D-values within each CBF combination, allowing for different directions of effects and is, therefore, less sensitive to main effects than the Z-test but more sensitive to interaction effects. The Z- and chi-square tests are both based on analysis of single markers. To take into account the additional information present in adjacent markers, D_hijk-values for all markers on a chromosome were analyzed jointly using a likelihood-based method equivalent to interval analysis (IA) that was described in Wang et al (2007). By analyzing each CBF combination as a separate family, the IA shares with chi square its sensitivity to interaction effects but is less powerful than the Z-test to detect main effects. The three tests just described (Z, χ², and IA) make use of D-values divided by their standard error (SE). Two additional tests: a three-way ANOVA and a nonparametric sign test were also used. These, although based on the same D-values as above, each use a different basis to test significance (see details in the following), in this way providing an additional control to the statistical calculations. Both ANOVA and the sign test share with the Z-test its sensitivity to main effects and insensitivity to interaction effects.

The individual statistical tests are now presented in turn.

Chi square:

A chi-square test was calculated across all 10 blood-type × family (BF_jk) combinations within each marker × cross (MC_hi) combination, as

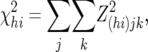where the parentheses in the subscript of Z_(hi)jk indicate that the summation was carried out separately across all BF_jk combinations within each MC_hi combination

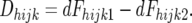dF_hijk1 and dF_hijk2 are the densitometric estimates of the frequency of the marker allele derived from line 2 in the resistant and susceptible pools, respectively. SE(D_hijk) are the standard errors of the D_hijk [see appendix a for derivation of SE(D_hijk)].

Summation, as noted, was across all 10 (BF)_jk combinations within each MC_hi combination. Consequently, the degrees of freedom (d.f.) was generally 10, but was occasionally less (4–9) according to the number of BF_jk combinations for which densitometric estimates of allele frequency were obtained within an individual MC_hi combination.

The P-value for the chi-square test was taken from the distribution of chi square by degrees of freedom. For chi-square analysis of the combined backcrosses, 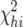and degrees of freedom were simply summed across BC-1 and BC-2.

Z-test:

A Z-test for a difference in allele frequencies between resistant and susceptible was calculated across all 10 blood-type × family (BF_jk) combinations within each marker × cross (MC_hi) combination, as

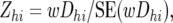where wD_hi is the weighted average D-value across the resistant and susceptible pools of the 10 BF_jk combinations within each of the MC_hi combinations, weighted by the number of individuals in each pool, and SE(wD_hi) is its standard error [see appendix a for derivation of wD_hi and SE(wD_hi)].

The P-value for the Z-test was obtained from the standard normal distribution. For the Z-test of the combined BC data, an average (wD_h) of the wD_hi-values across the two BCs and its standard error were used (see appendix a for details).

Interval analysis:

The interval analysis was implemented using the likelihood-based method of Wang et al. (2007). In this analysis, the different BF_jk combinations within crosses were treated as independent observations, and the joint likelihood for each cross was maximized with regard to the parameters of QTL location and estimate of the QTL frequency P(Q_(hi)jk) in the upper tail at the maximum position, where the parentheses indicate that the calculation was for each MC_hi combination separately, and the underline indicates that the maximization was across all BF_jk combinations within each MC_hi combination. This estimate was used to calculate an estimate of D_(hi)jk), namely D_(hi)jk = P(Q_(hi)jk) − (1 − P(Q_(hi)jk)). These D-values were then used to estimate the QTL effect for each backcross as described later. The analysis was carried out separately for each backcross and for the combined data.

ANOVA:

A three-way ANOVA was implemented using the Fit Model option in the JMP 5.1.2 statistical package (1989–2004, SAS Institute). Only main effects were tested because of limited degrees of freedom, using the following models:

• Model 1: D_h(i)jk = μ + M_h + BT_j + F_k + e_h(i)jk, where the parentheses in the subscript indicate that the model was run separately for the individual backcross analyses.

• Model 2: D_hijk = μ + M_h + BC_i + BT_j + F_k + e_hijk, for the combined analysis.

To the extent that some of the interactions are real, this will increase the error term, decreasing the significance of the results. However, not accounting for correlations that are expected to exist between D-values from linked markers will increase the significance since there are fewer effective degrees of freedom than assumed. Hence, these two effects will counteract to some extent. The ANOVA also provides estimates of the magnitude and direction of the main marker effect across BF_jk combinations within MC_hi combinations (model 1), or main marker (M_h) effects across CBF_ijk combinations (model 2) and tests whether these are significantly different from zero.

Nonparametric sign test:

In addition to the four statistical tests listed above, a nonparametric sign test (Walpole and Myers 1978) was used in the initial stage of the analysis for computational “quality control.” This test was based on the expectation that when marker–QTL linkage is present, the sign of the D_(hi)jk-values for that marker across all ten BF_jk combinations within the MC_hi marker–cross combination will be the same (all positive or all negative); while under the null hypothesis of no linkage, the sign of the D_(hi)jk-values should be equally distributed among positive and negative values. Major discrepancies between the marker P-values from the sign test and the marker P-values from the ANOVA or Z-tests were invaluable in alerting us to problems with procedures, data, or specific calculations. However, because the sign test tracks the same effects as ANOVA and the Z-test, but has less power than either, results with this test are not presented or discussed further.

Accounting for multiple tests:

To take into account the multiple-test situation while retaining power, a 20% “proportion of false positive” (PFP) threshold was used to determine the critical comparisonwise error rate (CWER) or P-value for declaring marker–QTL linkage (Fernando et al. 2004). For the IA test, the PFP calculation was done using all IA tests that were conducted on a chromosome at 1-cM intervals, as in the range of CWER values >0.001, there was a fairly smooth and monotonic relationship between rank number and PFP (see also Figure 2 of Lee et al. 2002).

Application of the PFP method requires prior estimation of the number of tests for which the null hypothesis is true (t_N), since only such tests can provide a false positive. This was done following the algorithm presented in Nettleton et al. (2006). Given an estimate of t_N, PFP for the ith test is calculated as: PFP_i = (P_it_N)/R_i, where P_i is the P-value of the ith test, when the tests are ranked by their P-values from lowest to highest, and R_i is the rank number of the ith test. The number of tests representing false null hypotheses, f_N, i.e., representing true marker–QTL linkages, can then be estimated as f_N = N − t_N and effective power as o_N/f_N, where o_N is the number of tests that are significant according to the designated significance level.

Estimating the effects of markers and QTL on survival time:

For each marker, M, with alleles M₁ and M₂ derived from line 1 and line 2, respectively, each pool contains two genotypic groups: either M₁M₁ and M₁M₂ for BC-1 or M₂M₂ and M₁M₂ for BC-2. With standard selective genotyping, the observed allele substitution effect is the observed quantitative difference between the two genotypic groups, α_P, taken over the selected tails of the population. With selective DNA pooling, α_P is estimated from the D-values (Darvasi and Soller 1994). Darvasi and Soller (1992, 1994) pointed out that in both cases, α_P is an exaggerated estimate of the actual substitution effect in the population as a whole, α_T, and provided an expression to estimate α_T from α_P with selective genotyping for a normally distributed trait. With appropriate modifications, this expression was adapted for the present data set (see appendix b for derivation). When applied to simulated survival data, the Darvasi and Soller (1994) expression appears to provide estimates of allele substitution effects that show a slight positive bias (∼10% greater) relative to the simulated effects. The same procedure was also used for the IA to estimate effects at QTL using estimates of D-values at the estimated QTL location obtained from that analysis (see also Wang et al. 2007).

Defining QTL containing chromosomal regions (QTLR) and testing for differences in allele substitution effects at the QTLR:

Because many of the markers were rather closely spaced, it is expected that a number of markers constituting a “block” may present significance if they span a chromosomal region containing a QTL. Indeed, examining the results showed that significant markers often appeared in blocks of two or more consecutive significant markers. Each such block was taken to constitute a QTL-containing region (QTLR). Blocks of significant markers were generally separated or flanked by runs of two or more consecutive nonsignificant markers. Each such block of nonsignificant markers was taken to define a chromosomal region from which QTL were absent (non-QTLR).

Many of the QTLR included a number of markers. All of these markers are presumed in linkage to the same QTL. Thus, they each present estimates for the allele substitution effect at the QTL. Consequently, differences in allele substitution effects of the various QTL could be tested by an ANOVA in which QTLR are taken as main effects and markers within QTLR as replicates. Since estimated marker effects for a given MC_hi combination are directly proportional to the D-values from which they are derived, differences in allele substitution effects at the different QTLR within the individual backcrosses were tested in practice by a one-way ANOVA of their respective marker D_(hi)jk-values, with QTLR as the main effect and estimated marker D_(hi)jk-values within a given QTLR taken as the individual variables, where the parentheses in the subscript indicate that the analysis is done within MC_hi combinations, and the underline in the subscript indicates that the analysis is done across all BF_jk combinations within a given MC_hi combination. ANOVA for the combined backcross was implemented in a similar way, except that analysis was done across all CBF_ijk combinations within a given M_h.

Significance of difference in map location of QTL identified in this study and in other independent studies reported in the literature:

A major objective of this study was to examine whether the QTL identified in experimental populations, were relevant with respect to QTL segregating in commercial populations. This was implemented as follows. To determine whether QTL reported on the same chromosome in two independent studies, S₁ and S₂, represent the same or different QTL, let L₁ be location of the QTL identified in S₁, and L₂ be the location of the QTL identified in S₂; N₁ and N₂, the total size of the respective mapping populations; and d, the standardized allele substitution effect at the QTL (under the null hypothesis that the QTL location and d are the same in the two populations). Then, significance of the difference in locations L₁ and L₂, with type I error α, is given by the integral of the standard normal curve from Zα_/2 to infinity, where

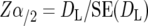D_L = L₁ − L₂, is the difference in map location between the QTL identified in the two studies, SE²(D_L) = SE²(L₁) + SE²(L₂), and SE(L₁) and SE(L₂) are the SE of QTL map location for the QTL at location L₁ and L_2, respectively.

For F₂ and BC populations and a saturated marker map, SE(L) can be estimated from the published expressions for the 95% confidence interval (C.I.) of QTL map location (Darvasi and Soller 1997; Weller and Soller 2003), namely: C.I.₉₅(L, F₂) = 1500/Nd²; C.I.₉₅(L, backcross) = 3000 cM/Nd². Noting that the C.I.₉₅ was set equal to 4SE(L), we have

RESULTS

In BC-1 the two BT genotypes (B2/B2 and B2/B15) were virtually identical in proportion of survivors, and differed by only 4.1 days (not significant by ANOVA) in favor of B2/B2 for mean survival time of the birds in the susceptible pool. In BC-2, however, B2/B15 was significantly more susceptible than B15/B15 (P < 0.01 by ANOVA): the proportion of survivors at the end of the test was 29.8% less than for B15/B15 (absolute value), and mean survival time of the birds in the susceptible pool was shorter by 8.2 days (Table 1).

On the basis of the ANOVA analysis, family effect approached significance in BC-1 and was borderline significant in BC-2 and the combined analysis (P < 0.05). The marker effect was highly significant in all populations.

Table 2 shows the distribution of the P-values of the various statistical tests, in bins of width 0.10. On the null hypothesis, the proportion of tests in each P-value bin is expected to be 0.10. For ANOVA, Z, chi square and IA there was a highly significant excess of tests in the lowest P-value bin (0–0.1) in all data sets (BC-1, BC-2, and the combined data) except for IA in BC-1.

TABLE 2.

Distribution of the P-values, estimated number of true and false null hypotheses of total tests, 0.20 PFP significance thresholds, number of observed significant results, and estimated power for ANOVA (AN), Z-test (Z), chi square (χ²) and interval analysis (IA), according to cross

	BC-1				BC-2				Combined
P-value bin	AN	Z	χ2	IA	AN	Z	χ2	IA	AN	Z	χ2	IA
0.0–0.1	0.17	0.17	0.17	0.08	0.18	0.21	0.15	0.15	0.18	0.21	0.17	0.18
0.1–0.2	0.08	0.11	0.07	0.09	0.11	0.13	0.10	0.09	0.08	0.08	0.08	0.10
0.2–0.3	0.09	0.11	0.08	0.12	0.13	0.07	0.06	0.09	0.11	0.11	0.07	0.07
0.3–0.4	0.08	0.10	0.06	0.09	0.10	0.10	0.06	0.08	0.10	0.09	0.04	0.08
0.4–0.5	0.08	0.09	0.09	0.14	0.05	0.07	0.09	0.05	0.10	0.12	0.08	0.06
0.5–0.6	0.11	0.08	0.10	0.09	0.05	0.08	0.06	0.07	0.08	0.06	0.06	0.06
0.6–0.7	0.11	0.11	0.05	0.07	0.08	0.07	0.10	0.11	0.08	0.10	0.08	0.07
0.7–0.8	0.09	0.07	0.17	0.06	0.12	0.10	0.09	0.10	0.11	0.09	0.11	0.07
0.8–0.9	0.12	0.08	0.09	0.10	0.11	0.07	0.12	0.09	0.10	0.06	0.18	0.07
0.9–1.0	0.08	0.09	0.12	0.16	0.09	0.11	0.16	0.16	0.08	0.07	0.12	0.24
Totala	180	180	180	2522	176	176	176	2469	198	158	158	2522
True	167	152	166	2522	143	145	166	2331	180	122	146	2267
False	13	28	14	0	33	31	10	138	18	36	12	255
PFP	0.006	0.006	0.016	0.005	0.014	0.025	0.013	0.008	0.013	0.020	0.020	0.019
Observed	7	7	14	69	15	26	12	96	14	17	15	217
Powerb	0.43	0.20	NC	NC	0.36	0.67	NC	NC	0.62	0.56	NC	NC

^aThe total number of tests in the combined analysis represents the total number of markers across either of the two BC populations for ANOVA, but the number of markers common to both BC populations for the Z and chi-square tests. For IA, the number of tests represents the maximum map size in centimorgans, as determined by the most proximal and most distal markers of each chromosome. These markers were identical for BC-1 and BC-2, with one exception, in which the BC-1 marker was 53 cM closer to the chromosome end than the BC-2 marker. Hence, the total number of tests in the combined IA (2522), was the same as that for the BC-1 population.

^bFor calculation of power, the number of observed significant markers (or 1-cM positions for IA) was reduced by 20% to account for false positives. Thus, power for AN in BC-1 was calculated as 0.8(7)/13 = 0.43.

For the BC-1, BC-2, and combined data, IA also showed a highly significant excess of tests in the highest P-value bin (0.9–1.0); a similar tendency, but not as strong or as significant was presented by the chi-square test. This excess cannot be due to linkage. Thus, the IA and chi-square tests appear to be conservative, which could be caused by some of their underlying assumptions not being met.

On the basis of the results in Table 2, the CWER P-values corresponding to the 0.20 PFP threshold level were calculated. These differed among crosses and test statistics but when averaged across all three data sets, threshold P-values for the various statistical tests were quite similar, being 0.011, 0.019, 0.016, and 0.011 for ANOVA, Z, chi square, and IA, respectively. These averaged thresholds were used to determine significance for the individual tests.

Table A1 shows markers that reached significance at PFP = 0.20 for at least two statistical tests (not including the sign test). These could be two different tests in any one of the three data sets, or the same test in any two of the three data sets. For these markers, CWER P-values are given for each of the four tests, according to cross and analysis. Comparing the observed number of significant results, with the estimated number of false null hypotheses (Table 2), provides estimates of the power of the analyses. For ANOVA and Z, power estimates ranged from 0.36 to 0.67, with a mean of 0.52 over all crosses. For chi square and IA, the conservative nature of the tests may be affecting power estimates in unknown ways, and hence the results are not presented.

TABLE A1.

Markers that reached significance (PFP = 0.20) for Z or IA in BC-1, BC-2, or combined analyses, and their P-values for all five tests

			BC-1					BC-2					Combined
Marker	Ch	P	AN	S	Z	χ2	IA	AN	S	Z	χ2	IA	AN	S	Z	χ2	IA
ADL0192	1	149					0.57	−0.01	0.41	−0.00	0.00	0.00	−0.01				0.00
LEI0146	1	169	0.08	0.53	0.04	0.03	0.18					0.01	0.08				0.00
MCW0115	1	518	0.42	0.21	0.26	0.25	0.24	0.03	0.01	0.01	0.15	0.04	0.03	0.01	0.01	0.14	0.03
ADL0350	1	523	0.65	0.53	0.45	0.27	0.32	0.01	0.01	0.00	0.11	0.03	0.04	0.03	0.01	0.11	0.03
GCT0032	1	523	0.31	0.21	0.19	0.53	0.32	0.01	0.01	0.00	0.04	0.03	0.01	0.01	0.00	0.11	0.03
ADL0185	2	95	0.62	0.53	0.41	0.77	0.87	0.04	0.01	0.01	0.24	0.19	0.07	0.03	0.02	0.51	0.95
LEI0043	3	9	−0.01	0.32	−0.00	0.02	0.19					0.98	−0.01				0.22
ADL0042	3	207					0.02	0.00	0.21	0.00	0.00	0.01	0.00				0.00
MCW0103	3	208	−0.00	0.06	−0.00	0.03	0.03	0.11	0.06	0.04	0.66	0.01	−0.26	1.00	−0.47	0.11	0.00
MCW0129	4	175	0.84	0.53	0.61	0.76	0.57	−0.01	0.21	−0.01	0.00	0.03	−0.13	0.65	−0.15	0.02	0.07
LEI0116	5	6	0.05	0.21	0.02	0.01	0.00	−0.79	1.00	0.91	1.00	1.00	0.22	0.37	0.07	0.16	0.10
LEI0082	5	32	0.23	1.00	0.12	0.00	0.00	−0.19	0.21	−0.36	0.04	0.17	−0.99	0.37	0.64	0.00	0.10
MCW0081	5	152	−0.00	0.06	−0.00	0.00	0.10	0.74	0.53	0.42	0.55	0.47	−0.06	0.37	−0.13	0.02	0.12
ADL0279	7	62	−0.11	0.21	−0.19	0.55	0.40	−0.00	0.01	−0.01	0.10	0.07	−0.00	0.01	−0.00	0.21	0.05
MCW0236	7	79	−0.88	1.00	0.89	0.54	0.68	−0.00	0.06	−0.01	0.07	0.06	−0.04	0.18	−0.09	0.16	0.03
LEI0158	7	91	−0.94	0.53	0.82	1.00	0.98	−0.00	0.21	−0.15	0.14	0.19	−0.00	0.65	−0.31	0.72	0.00
MCW0100	8	43	−0.96	1.00	−0.07	1.00	0.99					0.00	−0.96				0.00
ADL0154	8	46	−0.71	1.00	−0.93	0.93	1.00					0.00	−0.70				0.00
ADL0345	8	56	0.06	0.48	−0.24	0.07	0.50	0.01	0.06	0.00	0.00	0.00	0.00	0.06	0.00	0.00	0.00
ADL0021	9	48					0.30	0.01	0.01	0.00	0.12	0.05	0.01				0.06
LEI0028	9	51	−0.53	1.00	−0.71	0.53	0.26	0.00	0.01	0.00	0.01	0.02	0.08	0.07	0.02	0.05	0.01
LMU0006	9	51	−0.77	1.00	−0.99	0.31	0.26	0.00	0.06	0.00	0.01	0.02	0.07	0.18	0.02	0.02	0.01
LEI0197	9	56	−0.19	0.53	−0.29	0.04	0.11	0.05	0.21	0.01	0.28	0.11	0.64	0.65	0.33	0.06	0.02
LEI0083	15	3					0.49	−0.26	0.41	−0.44	0.01	0.01	−0.31				0.01
MCW0231	15	23	0.07	0.06	0.04	0.06	0.01	0.32	0.21	0.15	0.35	0.09	0.05	0.03	0.01	0.09	0.01
ROS0348	15	25	0.04	0.21	0.02	0.01	0.01	0.47	0.06	0.09	0.08	0.09	0.05	0.03	0.00	0.01	0.00
MCW0052	15	26	0.06	0.21	0.03	0.01	0.00	0.22	0.21	0.09	0.14	0.10	0.03	0.07	0.00	0.01	0.00
MCW0211	15	39	0.01	0.21	0.01	0.01	0.00	0.28	0.53	0.64	0.23	0.40	0.01	0.18	0.02	0.01	0.01
ADL0022	Z	0	0.00	0.01	0.00	0.01	0.27	0.10	0.53	0.09	0.08	0.54	0.00	0.03	0.00	0.01	0.32
ROS0309	Z	36	0.00	0.06	0.02	0.08	0.54	0.42	0.21	0.35	0.97	0.99	0.01	0.03	0.02	0.44	0.92
MCW0055	Z	37					0.59	0.13	0.21	0.14	0.84	0.98	0.12				0.92
MCW0258	Z	42	0.05	0.06	0.08	0.43	0.81	0.33	0.21	0.31	0.79	0.94	0.03	0.03	0.04	0.70	0.97
MCW0331	Z	43	0.01	0.21	0.02	0.17	0.73	0.00	0.06	0.00	0.03	0.89	0.00	0.03	0.00	0.00	0.87
ROS0301	Z	49	0.02	0.21	0.04	0.30	0.71	0.15	0.21	0.15	0.91	0.97	0.01	0.07	0.01	0.69	0.96
ADL0273	Z	52	0.05	0.21	0.09	0.00	0.37	0.33	0.53	0.27	0.12	0.87	0.04	0.18	0.04	0.00	0.60
MCW0241	Z	74	0.29	0.53	0.30	0.05	0.42	0.18	1.00	0.15	0.00	0.21	0.09	0.65	0.08	0.00	0.23
LPL	Z	103	−0.57	1.00	−0.78	0.26	0.82	0.00	0.53	0.00	0.00	0.03	0.04	0.65	0.05	0.00	0.18
LEI0075	Z	115	0.39	0.53	0.42	0.00	0.17	0.00	0.53	0.00	0.00	0.98	0.00	0.37	0.00	0.00	0.62

Underlined tests were significant at a PFP = 0.20. Ch, marker chromosome; P, position (marker location) (cM); AN, ANOVA; S, sign test; Z, Z-test; χ², chi-square test; IA, interval analysis; —, marker not analyzed.

Table 3 shows the QTLR and non-QTLR defined in this way. An exception was made for chromosome Z, where QTLR I and II were not separated by nonsignificant markers. In this case, two QTL were assumed on the basis of the overall length of the significant region which extended from 0 to 74 cM.

TABLE 3.

Chromosomal regions that contain QTL (QTLR) and that do not contain QTL, according to cross and statistical test

					Cross
Chra	Reg.	Type	M	Location (cM)	BC-1	BC-2	Comb.	Location IA (cM)
1	I	Non-Q	6	33–122
	II	QTLR	1	149		A, C	A, C	152 (140–174)
	III	Non-Q	19	169–442
	IV	QTLR	3	518–523		A, C	A
2	I	Non-Q	3	46–70
	II	QTLR	1	95		A	A
	III	Non-Q	25	119–400
3	I	QTLR	1	9	A, C		A
	II	Non-Q	6	116–183
	III	QTLR1	2	207–208	A	A, C	A, C	206 (190–211)
	IV	Non-Q	5	232–275
4	I	Non-Q	17	50–170
	II	QTLR	1	175		A, C	C
	III	Non-Q	4	187–196
5	I	QTLR	2	6–32	C		C	20 (0–54)
	II	Non-Q	9	83–128
	III	QTLR	1	152	A, C
	IV	Non-Q	4	153–198
7	I	Non-Q	2	0–56
	II	QTLR	3	62–91		A	A, C	90 (80–96)
	III	Non-Q	2	107–135
8	I	Non-Q	4	8–26
	II	QTLR	3	43–56		A, C	A, C	57 (40–83)
	III	Non-Q	4	96–109
9	I	Non-Q	1	43
	II	QTLR	4	48–56		A, C	A, C	51 (51–55)
	III	Non-Q	4	70–150
15	I	Non-Q	2	1–2
	II	QTLR	5	3–39	A, C	C	A, C	26 (3–39)
Z	I	QTLR	6	0–49	A, C	A	A, C
	II	QTLR	2	52–74	C	C	C
	III	Non-Q	2	87–97
	IV	QTLR	2	103–115	C	A, C	A, C	114 (112–114)

M, number of markers in the region; Comb., combined crosses; A, significant by Z-test or ANOVA; C, significant by chi square or IA; Location IA, location of peak of maximum significance (in parentheses, region of significance).

^aThe following chromosomes did not present any significant markers in either of the BC populations or in the combined analysis: chromosomes 6 (4 markers, 21–87 cM), 11 (3 markers, 0–68 cM), 13 (4 markers, 16–44 cM), 18 (3 markers, 7–47cM), 26 (4 markers, 33–67 cM), 12, 14, 19, 20, 27 (2 markers each, centimorgan locations unknown), and 10, 23, 24, E22, E26 (1 marker each, centimorgan locations unknown).

A total of 20 significant QTLR × BC combinations were uncovered, located on 10 of the 25 chromosomes included in the genome scan (GGA1, 2, 3, 4, 5, 7, 8, 9, 15, and Z). Fifteen chromosomes, with one to four markers per chromosome, did not carry any significant markers (see Table 3, footnote a, for details). Of the significant QTLR, 5 (33.3%) were common to both BC-1 and BC-2, 3 (20%) were significant only in BC-1, and 7 (47.7%) were significant only in BC-2. Thus, a total of 15 different QTLR were uncovered. Of the 20 significant QTLR × BC combinations, 4 (20%) were significant for the ANOVA and/or Z-tests only, 5 (25%) were significant for χ² and/or IA tests only, and 11 (55%) were significant for both ANOVA/Z- and χ²/IA tests. Thus, within the individual BCs, 75% of the uncovered QTL had a significant additive component, while only 25% were strongly interactive, with little or no additive effects. A virtually identical picture was seen for the 14 QTLR found significant in the combined analyses.

The effect on survival time was calculated separately for each M × BC × F combination in each of the QTLR as described in appendix b, using the same wD_hi-value as used for the Z-test for that M × BC × F combination, and using the estimated D-value at the marker for the IA. The average survival time over all M × F combinations of a given QTLR within crosses are presented in Table A2, separately by cross. When all markers in the QTLR regions were considered, 73.3, 78.1, and 77.8% of alleles from line 2 were associated with positive (increasing) effects on survival time for the BC-1, BC-2, and the combined analysis, respectively. When all markers in the non-QTLR regions were considered (data not shown), percentages of markers with positive D-values were significantly lower (P < 0.0001 by chi-square contingency test), at 55.8, 62.7, and 56.7%, respectively. This indicates that in the QTLR regions, positive effects of the line 2 alleles on survival time predominated, as expected.

TABLE A2.

The effect (in days) of each marker in the QTLR on survival time by cross

QTLR	Marker	Position (cM)	BC-1	BC-2	Combined
1-II	ADL0192	149		−10.60
1-IV	MCW0115	518	(3.91)	9.20	6.55
1-IV	ADL0350	523	(2.65)	10.05	6.35
1-IV	GCT0032	523	(4.65)	11.13	7.89
2-II	ADL0185	95	(2.83)	8.66	5.74
3-I	LEI0043	9	−14.47
3-III	ADL0042	207		11.96
3-III	MCW0103	208	−10.43	(7.00)	(−1.72)
4-II	MCW0129	175	(1.77)	−8.60	(−3.41)
5-I	LEI0116	6	(8.04)	(0.47)	(4.25)
5-I	LEI0082	32	(5.33)	(−3.14)	(1.10)
5-III	MCW0081	152	−9.65	(2.54)	(−3.56)
7-II	ADL0279	62	(−4.67)	−8.78	−6.73
7-II	MCW0236	79	(0.50)	−8.46	(−3.98)
7-II	LEI0158	91	(0.76)	(−5.55)	(−2.40)
8-II	MCW0100	43	(0.85)
8-II	ADL0154	46	(−0.28)
8-II	ADL0345	56	(8.38)	11.17	9.78
9-II	ADL0021	48		10.00
9-II	LEI0028	51	(−1.19)	12.18	5.49
9-II	LMU0006	51	(−0.001)	11.53	5.76
9-II	LEI0197	56	(−3.62)	8.26	(2.32)
15-II	LEI0083	3		(−3.22)
15-II	MCW0231	23	(7.47)	(4.86)	6.16
15-II	ROS0348	25	(8.26)	(5.77)	7.02
15-II	MCW0052	26	(7.77)	(5.69)	6.73
15-II	MCW0211	39	9.69	(1.66)	5.68
Z-I	ADL0022	0	14.68	(7.11)	10.89
Z-I	ROS0309	36	(11.18)	(4.21)	7.70
Z-I	MCW0055	37		(6.66)
Z-I	MCW0258	42	(8.14)	(4.80)	6.47
Z-I	MCW0331	43	(10.92)	14.48	12.70
Z-I	ROS0301	49	(9.39)	(6.41)	7.90
Z-II	ADL0273	52	(8.06)	(4.77)	6.42
Z-II	MCW0241	74	(4.84)	(6.11)	(5.48)
Z-IV	LPL	103	(−0.95)	13.45	(6.25)
Z-IV	LEI0075	115	(4.07)	14.49	9.28

QTLR are designated according to Table 4. Ch, chromosome; cM, marker location on the chromosome in centimorgans. In parentheses, estimates based on nonsignificant marker effects.

Examination of estimated effects for individual markers within QTLR (Table A2) showed a relatively high consistency of effects across markers within QTLR within crosses and major differences between QTLR within crosses; in particular some QTLR were characterized by positive effects and others by negative effects. The ANOVA analyses showed that for all crosses and for the IA, differences among QTLR were highly significant (P < 0.0001) (data not shown). On this basis, the mean effect on survival time of all markers within a QTLR was taken to represent the effect of the QTLR on survival time. These are shown in Table 4, separately for BC-1, BC-2, combined analysis, and IA. Effects are given for all 15 defined QTLR, whether or not they were significant in the particular population or analysis, but effects based on nonsignificant QTLR are shown in parentheses. Effects in BC-1 and BC-2 often differed greatly. Effects in combined and IA were generally very similar and approximately equal to the mean effect across BC-1 and BC-2.

TABLE 4.

The average effect of each QTLR on survival time in days and inferred type and dominance status of the resistance/susceptibility allele at the QTL for line 2, line 1, and the F₁ cross between them

QTLR	BC-1	BC-2	Comb	IA	Line 2	Line 1	Cross
1-II	ND	−10.60	ND	−1.39	s	R	Rs
1-IV	(3.73)	10.13	6.93	(7.37)	r	S	rS
2-II	(2.83)	8.66	5.74	(5.66)	r	S	rS
3-I	−14.47	ND	ND	(−12.70)	S	r	rS
3-III	−10.43	9.48	(−1.72)	0.98	R	S	RSa
4-II	(1.77)	−8.60	−3.41	(−2.52)	s	R	Rs
5-I	6.68	(−1.34)	2.67	(2.09)	R	s	Rs
5-III	−9.65	(2.54)	(−3.56)	−2.52	S	r	rS
7-II	(−1.14)	−7.60	−4.37	−7.56	s	R	Rs
8-II	(2.98)	11.17	9.78	8.78	r	S	rS
9-II	(−1.61)	10.49	4.52	5.45	r	S	rS
15-II	8.30	2.95	6.40	6.41	R	s	Rs
Z-I	10.40	7.28	9.13	(13.75)	R	S	Rb/S
Z-II	6.45	5.44	5.95	(6.77)	R	S	Rb/S
Z-IV	1.56	13.97	7.77	(8.78)	R	S	Rb/S
Sum S	−6.20	44.38	51.85	10.15	10R/5S	5R/10S	8R/6Sb 5R/9S
Sum A	7.40	53.98	45.84	39.36

Effects calculated using a weighted D-value for BC-1, BC-2, and combined crosses (Comb) or an estimated D-value obtained from the interval analysis (IA) as described in the text are shown. ND, not done; Sum S, sum of estimated effects on survival time of significant QTLR; Sum A, sum of estimated effects on survival time of all QTLR. Inferred allele type and dominance status: line 2, line 2 allele: R, r, resistance alleles, dominant or recessive, respectively; S, s, susceptibility alleles, dominant or recessive, respectively. Line 1, line 1 allele. Cross, inferred genotype of the cross of the two pure lines. Values in parentheses were not significant for that test in that cross.

^aDominance status in cross cannot be inferred from dominance status in the BCs.

^bStatus of locus depends on direction of cross. R, if male is line 2; S, if male is line 1.

Considering all QTLR, whether significant or not: 9 of 14 effects were positive for BC-1, 10 of 14 effects were positive for BC-2, 9 of 13 effects were positive for the combined analysis, and 10 of 15 effects were positive for IA. Considering only significant QTLR, 5 of 8 significant QTLR were positive in BC-1, 9 of 12 were positive in BC-2, and 9 of 11 were positive in the combined analysis, but only 3 of 6 significant QTLR were positive in the IA. Thus, in the BC-2 and combined analysis there was a clear predominance of positive effects associated with line 2 alleles, as expected from the difference between the parental lines. In BC-1, however, a relatively large number of negative effects were associated with line 2 alleles.

Since D-values were calculated as the frequency of the line 2 allele in the resistant pools minus frequency of the line 2 allele in the susceptible pools, positive QTLR effects on survival time represent positive effects of the line 2 QTL alleles on resistance, and negative effects of QTLR on survival time represent negative effects of the line 2 QTL alleles on resistance. Thus, summing the effects of all QTLR within a population or analysis (whether significant or not) provides an estimate of the expected difference in mean survival time between line 2 and line 1, which can be attributed to the identified QTL. When this is done, estimates of 7.4, 54.0, 45.8, and 39.4 days are obtained for BC-1, BC-2, the combined analysis, and IA estimates, respectively. The estimates for BC-2, the combined analysis, and IA are roughly similar and indicate a difference in survival time for line 2 and line 1 of ∼46 days, under the conditions of the experiment. It may be advisable to reduce this somewhat to take into account the effect of nonnormality, as indicated above. Nevertheless, the experiment may have identified an appreciable proportion of the line 2 resistance QTL. The estimate from BC-1 is clearly different; possible reasons for this will be developed in the discussion.

DISCUSSION

Comparison to the literature:

Effects on MDV resistance have been reported for the MHC (B blood group, reviewed in Weigend et al. 2001), growth hormone gene (Kuhnlein et al. 1997; Liu et al. 2001, 2003), and the stem lymphocyte antigen 6 complex locus E (LY6E) gene (Liu et al. 2003). Strong evidence for involvement of the MHC was also found in this study (Table 1). Evidence was not found, however, for a QTL in the vicinity of the LY6E gene (presumed location at 407 cM on chromosome 2, corresponding to non-QTLR region 2-III of Table 3), while markers in linkage to the GH gene were not included in this study. With respect to previous QTL mapping studies, Vallejo et al. (1998) mapped QTL affecting MDV resistance in an F₂ population derived from a cross between the MDV-resistant inbred White Leghorn line 6₃ and MDV-susceptible inbred White Leghorn line 7₂. They used selective genotyping with a total population size N = 272, a rather sparse marker map of 65 microsatellite markers, and mapped with respect to nine different “traits” (i.e., criteria for MDV resistance). Yonash et al. (1999) followed up Vallejo et al. (1998) by genotyping all 272 individuals and adding an additional 49 markers, for a total of 127 markers.

To determine whether the Yonash et al. QTL corresponded to the QTL identified on the same chromosomes in this study, the standard error of the difference between QTL map locations obtained in Yonash et al. (1999) and this study was calculated as described in materials and methods, using the following values for N and d: For the Yonash et al. (1999) study, N = 272, and d can be estimated from the average proportion of variance, V_Q, explained by the individual QTL (see Table 2 column R² of the Yonash et al. 1999 study), according to the expression V_Q = 0.5d² for an additive QTL in an F₂ population (adapted from expression 8.7 of Falconer and Mackay 1996, noting that for an F₂ population p = q = 0.5). For the individual QTL identified in the Yonash et al. (1999) study V_Q ranged from 0.014 to 0.098, averaging 0.0353. Substituting appropriately, we obtain d = 0.265 and SE(L₁) = 19.5 cM. For this study we have N = 1000 for each of the BCs. Using the same d estimate, we obtain SE(L₂) = 10.6. These are underestimates: the estimate for L₁, because the Yonash et al. marker map is far from saturated; the estimate for L₂, because the QTL map locations for this study are based on pool analyses, which introduce additional sources of error. Adding 10% to each SE to account for this, we obtain SE(D_L) = 24.4. Taking 2SE(D_L) as the least significant difference (LSD) at 5% level of significance, we have LSD = 48.8 cM. Locations L₁ and L₂ farther apart than this will be considered as representing different QTL; locations closer than this, as representing the same QTL.

Yonash et al. (1999) identified 13 QTL affecting various aspects of MDV resistance that reached the “suggestive” or “significance” levels of significance defined according to the guidelines of Lander and Kruglyak (1995). For purposes of comparison of Yonash et al. (1999) to this study we considered only QTL that reached the significance level and took the marker closest to the peak to represent the location of the QTL. This resulted in four identified QTL in the Yonash et al. (1999) study, which can be compared to the QTL identified on the same chromosomes in this study, as follows:

• Chromosome 2: Yonash et al. identified a QTL at 90 cM. QTLR 2-II of this study is located at 95 cM. Thus, DL = 5 cM, not significant (NS).

• Chromosome 4: Yonash et al. identified a QTL at 138 cM. QTLR 4-II of this study is located at 175 cM. Thus, DL = 37 cM, NS.

• Chromosome 7: Yonash et al. identified a QTL at 130 cM. QTLR 7-II of this study is located at 62–91 cM, with mean location at 76.5 cM. Thus, DL = 53.5, which is just past point of significance, but does not take into account that this is the largest difference from among four, so that a Bonferroni correction would be appropriate. With Bonferroni correction, this corresponds to P = 0.11, which is NS.

• Chromosome 8: Yonash et al. identified a QTL at ∼25 cM. QTLR 8-II of this study is located at 43–56 cM, mean location at 49.5 cM. Thus, DL = 24.5 cM, NS.

Thus, in this study, QTL were found that corresponded in location to all four of the significant QTL identified in the Yonash et al. (1999) study. Taking into account that both this study and the Yonash et al. (1999) study involved White Leghorns, and the narrow lineage of all White Leghorns, it would seem reasonable to conclude that these represent QTL identical by descent. This supports the usefulness of the ADOL experimental Leghorn layer lines as sources of mapping and QTL information for commercial Leghorn lines and validates these four QTL as representing true effects.

In addition to the four QTLR included in the above list, this study also uncovered QTL on chromosomes 1, 3, 5, 9, 15, and Z that were not identified by Yonash et al. Recently, McElroy et al. (2005) reported an analysis of an independent hatch from the same BC-1 population of the current report. This hatch had only 4.3% survivors compared to 50.2% survivors in the BC-1 hatch of this study. McElroy et al. (2005) used selective individual genotyping and a Cox proportional hazards model as well as linear regression to analyze the data. They found seven suggestive markers that were significant at PFP < 0.2. These corresponded to QTLR 2-II, 5-I, Z-I, Z-II, and Z-IV of this study. Thus, of the 15 QTLR identified in this study, QTLR 2-II was identified by both Yonash et al. (1999) and McElroy et al. (2005); QTLR 4-II, 7-II, and 8-II were identified by Yonash et al. (1999); and QTLR 5-I, Z-I, Z-II, and Z-IV were identified by McElroy et al. (2005). Of the seven QTLR remaining, QTLR 1-II and 1-IV may possibly have been identified at suggestive levels by Yonash et al. (1999), although reported locations for the Yonash et al. chromosome 1 QTL differ from those for QTLR 1-II and 1-IV by considerably more than the LSD. QTLR 3-I, 3-III, 5-III, 9-II, and 15-II represent new QTLR not previously reported. The high repeatability of the results with independent populations and different MDV-related traits, genotyping procedures, and statistical methods, strongly support the validity of the present results.

Comparison of results in BC-1 and BC-2:

Of the 15 QTL uncovered in the present experiment, 5 (only one-third) were found in both BC-1 and BC-2, 7 were found uniquely in BC-2, and 3 were found uniquely in BC-1. The same F₁ sires generated both of the BC populations, and the experimental procedures and markers used in the analysis of these populations were more or less identical. Consequently, the apparently low proportion (denoted Q) of QTL mapped in both populations cannot be attributed to such factors as differences in the alleles in the two populations, the criteria for defining the target trait, the markers used, or the analytical procedures. Two models can be offered to explain the apparently low overlap in QTL identified in the two BCs. Model 1 attributes the unique alleles of each BC to the effects of dominance. On this model, the 7 QTL uniquely mapped in BC-2 represent loci at which the line 2 allele is recessive (and hence have measurable effects in BC-2); the 3 QTL uniquely mapped in BC-1 represent loci at which the line 2 allele is dominant (and hence have effects only in BC-1). Model 2 assumes additive gene action at a proportion (denoted Π) of the QTL, so that these QTL could potentially come to expression in both of the BCs. On this model, the unique alleles of each BC are attributed to the incomplete power of the two BC mapping populations. In particular, if power of the experiment for a given QTL in an individual BC population is π, then the likelihood that the given QTL will be identified in both BCs will equal π², and the expectation of Q = Ππ². In this study, the observed value of Q was 0.33. On the assumption that all QTL are additive (i.e., Π = 1), we obtain π = 0.57 as the average power of the two mapping populations. This compares well with the average power estimate of 0.52 for this study (Table 2). Thus, on model 2, the value Q = 0.33 for the observed proportion of QTL mapped in both populations implies that essentially all QTL are additive and potentially expressed in both BCs.

Resistance alleles in line 1 and line 2:

Line 2 alleles had positive effects at 9 of the 15 QTLR and negative effects at 5 of the 15 QTLR (with positive effects at the line 1 alleles at these QTL). This is consistent with the overall greater resistance of line 2, but also shows that line 1 carries a number of cryptic resistance alleles that are not present (or are present only at low frequencies) in line 2. The mixed effects at QTLR 3-III at which the line 2 allele had positive effects on BC-2 and negative effects in BC-1 may be due to interaction of QTL and genetic background (Carlborg and Haley 2004; Carlborg et al. 2004).

Summing allelic effects across all significant QTLR for BC-2 yields a total expected difference of 48.93 days in mean survival time for line 2 as compared to line 1; the corresponding sum is only 7.84 days when based on effects estimated in BC-1. The difference between summed effects for BC-1 and BC-2 is greater when based on autosomal QTLR only. In this case, summed effects come to −10.57 days for effects estimated in BC-1 and 22.24 days for effects estimated in BC-2. On model 1, which attributes lack of overlap in autosomal QTL in BC-1 and BC-2 to dominance, this discrepancy can be explained by assuming that most of the line 2 resistance alleles are fully recessive, and hence have a positive effect in BC-2, but do not have a measurable effect in BC-1; while line 2 susceptibility alleles are dominant and hence have a measurable effect in BC-1, but not in BC-2. Recessiveness of line 2 resistance alleles would also explain why it is primarily the Z chromosome QTL that were identified in both BCs, since in this case, recessiveness does not interfere with locus effect. Model 2, which attributes lack of overlap to incomplete power, does not offer any explanation other than chance variation for these chromosome and BC specific effects. The reversed effects of QTLR 3-III in BC-1 (negative) and BC-2 (positive) can also be interpreted somewhat more comfortably by model 1 as due to background modifier genes reversing direction of dominance, which is well recognized in the literature, than as background modifier genes reversing direction of a main effect, which does not have precedents in the literature. For these reasons we tend to favor model 1. Table 4 summarizes the inferences of this model as a genetic formula for line 2 and line 1 and the cross between them. According to this interpretation, the resistance of the cross will depend critically on whether line 2 or line 1 is the male parent, since this will determine the resistance status of the three QTLR on the Z chromosome.

Possible recessiveness of resistance alleles:

The inferred recessiveness of many of the resistance alleles is somewhat surprising, as on general principles, it is expected that alleles with positive effects on fitness will be dominant or at least additive in nature. However, this is not unprecedented. In a large scale study of the inheritance of trypanotolerance in the F₂ cross between trypanotolerant N'Dama cattle of West Africa and the susceptible Kenyan Boran cattle, 12 of 35 significant effects on trypanotolerance-associated traits showed a recessive mode of action (Hanotte et al. 2003). Classic retroviral resistance alleles (tva, tvb, etc.) are also recessive, and this is just what would be expected of loss-of-function alleles in a viral receptor. As noted above (in The resource populations), the F₆ generation of the cross between line 1 and line 2 presented a high level of mortality. This is also consistent with the recessive status of some of the resistance alleles.

The ability of the cross between line 2 and line 1 to uncover marker–QTL linkage depends critically on the existence of a major difference in allele frequency at the QTL between the two lines. Some of these QTL may be at fixation for the resistance allele in line 2, while line 1 may have lost the resistance allele and hence be at fixation for the susceptibility allele. Selection within the lines would not be effective in increasing resistance with respect to QTL of this type. However, the presence of significant differences among families within BCs, as shown by the ANOVA analysis, implies that the populations are still segregating for at least some of the QTL affecting resistance. It is these QTL, among others, that provide the continued response to selection for resistance that is observed within these lines. The inferred recessiveness of many of the resistance alleles would explain the ability of the populations to retain considerable genetic variation in the presence of long-term selection. For recessive alleles, selection would become effective only as the alleles approached high frequencies in the population, at which point additive genetic variation attributed to the locus is maximized (Falconer and Mackay 1996). Thus, the ability of the cross to uncover marker–QTL linkage is compatible with continued response of the population to selection and with high frequency of resistance alleles in the populations that are responding. Thus, there is a reasonable possibility that the QTL uncovered in the F₂ cross of these lines are also, at least in part, still segregating within the lines and contributing to response to selection. In this case, high-resolution mapping within the lines might uncover markers in linkage disequilibrium that could be used for within-line MAS.

APPENDIX A: STANDARD ERROR OF D-VALUES

As described in materials and methods, two sets of D-values denoted D_hijk and wD_hi were calculated. These and their standard errors were used, respectively, in the chi-square and Z-tests for marker–QTL linkage. These D-values and their standard errors are now defined and derived in detail.

D_hijk and SE(D_hijk):

As defined in materials and methods,

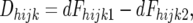where dF_hijk1 and dF_hijk2 are the densitometric estimates of the frequency of the marker allele derived from line 2 in the resistant and susceptible pools, respectively. The dF_hijk have two components, the actual allele frequency in the pool, F_hijk, and a technical error of estimation, T_hijk, so that dF_hijk1 = F_hijk1 + T_hijk1 is the densitometric estimate of the frequency of the marker allele derived from line 2 in the hijkth resistant pool, and dF_hijk2 = F_hijk2 + T_hijk2 is the densitometric estimate of the frequency of the marker allele derived from line 2 in the hijkth susceptible pool, where T_hijk1 and T_hijk2 are the technical errors of estimates of the frequency of the allele derived from line 2 in the hijkth resistant and susceptible pools, respectively, and F_hijk1 and F_hijk2 are the actual frequencies of the allele derived from line 2 in the hijkth resistant and susceptible pools, respectively.

We can further define

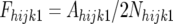where A_hijk1 and A_hijk2 are the number of alleles derived from line 2 (the more resistant line) in the hijkth resistant and susceptible pools, respectively, and N_hijk1 and N_hijk2 are the number of individuals in the hijkth resistant and susceptible pools, respectively. Then

where V_T is the technical error variance of pool densitometry, estimated as described in the last section of this appendix. SE²(F_hijk1) and SE²(F_hijk2) can be estimated from expected allele frequency in the resistant and susceptible pools under the null hypothesis, on the following argument.

The N_ijk1 and N_ijk2 are constants for each CBF_ijk combination. Considering first the allele frequency in the resistant pools, N_hijk1 alleles in the resistant pools of the backcross individuals are derived from the recurrent parent and an equal number of alleles are derived from the F₁ parent. Since the recurrent parent is monomorphic, the alleles derived from this parent are not a source of variation for A_hijk1. Thus, all sampling variation in A_hijk1 comes from segregation in the F₁ parent. Since the frequency of line 2 alleles in the F₁ parent is 0.5, A_hijk1 is a binomial variable with expectation 0.5N_hijk1 and binomial sampling variance 0.25N_hijk1. Putting all this together, we have

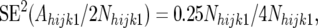and

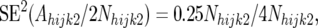so that

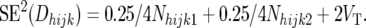wD_hi and SE(wD_hi):

For the Z-test, a weighted average D-value, wD_hi and its standard error were calculated as follows across the resistant and susceptible pools of the 10 BF_jk combinations within each of the MC_hi combinations,

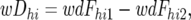where wF_hi1 and wF_hi2 are the weighted average densitometric frequencies of the line 2 allele across the 10 resistant and 10 susceptible pools, respectively, of the individual MC_hi; weighting was according to N_ijk1 or N_ijk2, the number of individuals in the ijkth resistant or susceptible CBF_ijk pool, as the case might be.

Without going into detail, but following the same reasoning as applied to SD²(D_hijk), we obtain

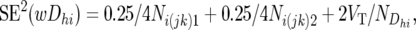where,

N_i(jk)1 and N_i(jk)2 are the total numbers of individuals summed across the 10 resistant and 10 susceptible pools, respectively, of the ith backcross, and 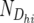is the number of wD_hi-values obtained for M_h (since not all pools gave a result for each marker, this was in the range of 4–10).

For the Z-test of the combined BC data, the average (wD_h) of the wD_hi-values across the two BCs, and its standard error and corresponding Z-values were calculated as

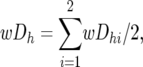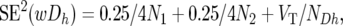and

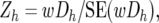where N₁ is the total number of individuals summed across the resistant pools of both backcrosses, N₂ is the corresponding value for the susceptible pools of both backcrosses, and N_Dh is the number of wD_h obtained for M_h (since not all pools gave a result for each marker, this was in the range of 14–20).

Technical error variance, V_T:

In addition to the pools described in the materials and methods a supplementary pair of pools, denoted “joint pools” were constructed within each of the four CB_ij combinations. The joint resistant pool contained DNA of all individuals in the resistant pools of the five families for that CB_ij combination; corresponding joint susceptible pools were also formed within each of the four CB_ij combinations. Consequently, for each of the CB_ij combinations, marker D-values based on the joint pools could be calculated as

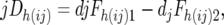whered_jF_h(ij)1 and d_jF_h(ij)2 are the densitometric frequency of the line 2 alleles of the hth marker in the joint resistant and joint susceptible pools, respectively, of the CB_ij combination.

A corresponding set of D-values, aD_h(ij)k was calculated from the individual D_hijk-values, as the average of the individual D_h(ij)k-values of the five families within each of the CB_ij combinations,

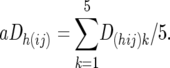These two sets of marker D-values were used to obtain an estimate of the technical error variance, as follows. For each CB_ij combination the difference between the two D_h(ij)-values for each marker, E_h(ij) was calculated as

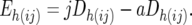Since exactly the same individuals are present in jD_h(ij) and aD_h(ij), the values obtained for the E_h(ij) are due solely to difference in the technical error acting on the individual jD_h(ij)- and aD_h(ij)-values. Since the jD_h(ij) are based on single resistant and single susceptible pools, the technical error variance of these measurements is simply V_T. The aD_h(ij), however, are based on the average of five pools. Hence, the technical error variance of these averages will be V_T/5. Thus, the variance of E_h(ij) is expected to equal

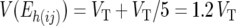and

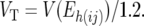APPENDIX B: ESTIMATING THE EFFECTS OF INDIVIDUAL MARKERS ON SURVIVAL TIME

Let P_R and P_S be the proportion of total population selected to construct the resistant and susceptible pools; let α_P be the observed quantitative difference between the mean survival time of the two genotypic groups (M₁M₁ and M₁M₂ for the backcross to line 1; M₂M₂ and M₁M₂ for the backcross to line 2) taken over both of the selected tails of the population; and let α_T be the actual substitution effect in the population as a whole. Then, substituting in the Darvasi and Soller (1994) expression gives

where 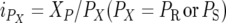is the selection intensity of the pool, X_P is the ordinate of the standard normal distribution at the point Z_P, which cuts off proportion P of the distribution.

In this study, P_S = 0.20 for both BC-1 and BC-2; P_R = 0.50 for BC-1 and 0.53 for BC-2.

With pool data, α_P is calculated as

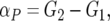where G₂ is the mean of individuals having the genotype which received the line 2 allele from the F₁ parent taken over the R and S pools. That is, for BC-1, G₂ is the mean of the M₁M₂ individuals; for BC-2, G₂ is the mean of the M₂M₂ individuals. G₁ is the corresponding mean for the individuals that received the line 1 allele from their F₁ parent, again taken over both pools, and

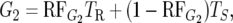where T_R and T_S are the mean survival times of the individuals in the R and S pool, respectively.

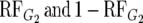are the relative frequencies of G₂ in the R and S pools, respectively:

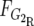and 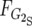are the frequency of G₂ in the R and S pools, respectively. G₁ is calculated accordingly.

The Darvasi and Soller (1994) expression is based on the assumption of a normal distribution which is violated in our case, due to the right skewed nature of the survival data. McElroy et al. (2006) simulated survival following MD challenge using a Cox proportional hazard model. Marker-associated effects on survival were obtained using a linear-regression model, under various assumptions of QTL effect and degree of censoring, and assuming selective genotyping of 20% per tail. Effects obtained on the linear model with selective genotyping were consistently ∼2.2 times the true effects. With selective genotyping at a proportion selection of 20%, the expected bias in estimated effect is 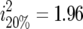-fold. Thus, when applied to survival data, the Darvasi and Soller (1994) correction factor appears to provide estimates of QTL effect that are ∼10% greater than the actual effects.