An annular superposition integral for axisymmetric radiators

Abstract

A fast integral expression for computing the nearfield pressure is derived for axisymmetric radiators. This method replaces the sum of contributions from concentric annuli with an exact double integral that converges much faster than methods that evaluate the Rayleigh-Sommerfeld integral or the generalized King integral. Expressions are derived for plane circular pistons using both continuous wave and pulsed excitations. Several commonly used apodization schemes for the surface velocity distribution are considered, including polynomial functions and a “smooth piston” function. The effect of different apodization functions on the spectral content of the wave field is explored. Quantitative error and time comparisons between the new method, the Rayleigh-Sommerfeld integral, and the generalized King integral are discussed. At all error levels considered, the annular superposition method achieves a speed-up of at least a factor of 4 relative to the point-source method and a factor of 3 relative to the generalized King integral without increasing the computational complexity.

I. INTRODUCTION

Many radiators in biomedical ultrasonics, SONAR, and nondestructive testing have a spatially varying particle velocity on the piston surface. This variation in surface velocity, or apodization, significantly alters the beam pattern compared to a radiator with uniform velocity. In order to accurately model pressures generated by these transducers, this apodization must be considered.^1,2 Although a formal solution to this problem is given by the Rayleigh-Sommerfeld diffraction integral³ or the King integral,⁴ these solutions can be poorly behaved numerically, especially near the source. In the case of the King integral, the integrand is singular, which leads to slow convergence relative to other integral expressions. Therefore, many specialized solutions have been developed to handle piston radiators, including series solutions in terms of spherical wave functions,^5-7 single-integral expressions based on the impulse response,^8-10 and transient single-integral expressions.¹¹ Recent series approaches have considered circular sources in finite baffles¹² and resilient disks¹³ with nonuniform surface velocity distributions.

To overcome the difficulties associated with the Rayleigh-Sommerfeld and generalized King integrals, an axisymmetric solution to the piston radiator problem is derived. Based on the fast nearfield method (FNM) for radiators with uniform surface velocity,^14-16 the proposed annular superposition method calculates the pressure fields generated by apertures where the surface velocity is a function of the radial variable. As an extension of the FNM expression derived in Ref. 14, this annular superposition method has a numerically well-behaved integrand that rapidly converges within the nearfield region of the radiator. Unlike the impulse response or Schoch solutions, the resulting annular superposition integral is defined by a single expression that describes the pressure throughout the entire computational domain.

After classical solutions to the apodized piston problem are reviewed, the method based on the annular superposition integral is derived subject to an arbitrary axisymmetric surface velocity distribution. This new method is applied to the “smooth piston” model and polynomial apodization functions. In addition, the method is generalized to the case of transient excitations. Example fields are computed and the spectral content of apodized wave fields are examined. Transient wave fields are also presented. An error analysis and comparison of the annular superposition method to the standard point-source approach is performed. The results show that the annular superposition integral achieves a speed-up by a factor of 4 relative to the Rayleigh-Sommerfeld integral at all error levels considered.

II. NEARFIELD CALCULATIONS FOR A CIRCULAR PISTON

Before the annular superposition integral is derived, two classical solutions to the baffled piston problem are reviewed: the Rayleigh-Sommerfeld and King integrals. Both the Rayleigh-Sommerfeld and the generalized King integral will be quantitatively compared to the proposed method.

A circular aperture with radius a, located in the x−y plane, radiates into a homogeneous acoustic half-space with constant density ρ and sound speed c. Initially, the excitation is assumed to be single frequency with angular frequency ω. The velocity distribution is assumed symmetric with respect to the angle θ lying in the x−y plane, allowing all apodization and phasing information to be encoded in an aperture function q(σ), where σ is radial distance. Figure 1 displays the geometry and notation used in the subsequent derivation. Since any realistic transducer has finite extent, q(σ) is assumed to be zero outside the interval [0,a].

FIG. 1.

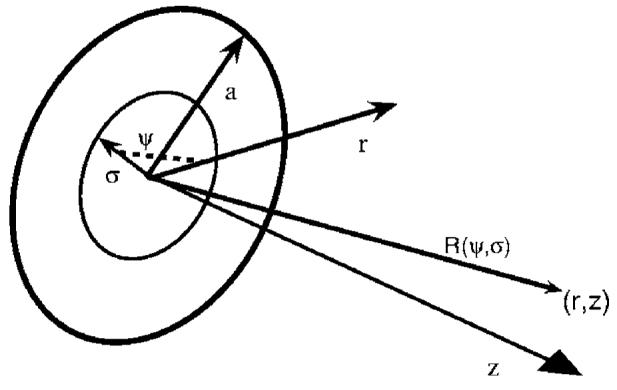
Coordinate axis used in the derivation. A piston of radius a is excited by a radially varying particle velocity specified by an aperture function q(σ), where σ is the radial position on the piston. The radiator is surrounded by an infinite rigid baffle in the z=0 plane. The angle ψ and relative distance R(ψ,σ) correspond to the notation used in Eq. (1).

A. Rayleigh-Sommerfeld integral

The Rayleigh-Sommerfeld diffraction integral, evaluated with the point-source approach,³ is a standard method for evaluating pressure fields generated by acoustic radiators. The Rayleigh-Sommerfeld integral analytically sums spherical wave contributions from each point on the aperture. In cylindrical coordinates, the Rayleigh-Sommerfeld integral is given by

$$\widehat{p}(r,z;\omega )=\frac{\mathit{jk}\rho c}{\pi }{\int }_0^a\sigma q\left(\sigma \right){\int }_0^{\pi }\frac{e^{-\mathit{jkR}(\psi ,\sigma )}}{R(\psi ,\sigma )}d\psi d\sigma$$ (1)

with $R(\psi ,\sigma )=\sqrt{z^2+{\sigma }^2+r^2-2r\sigma \cos \psi }$. Through the cylindrical symmetry of R(ψ,σ), the integrand of Eq. (1) evaluated for ψ ∈ [0,π] is replicated for ψ ∈ [π,2π], so the limits of integration are reduced to [0,π]. Note that Eq. (1) possesses a 1/R singularity.

B. Generalized King integral

The generalized King integral utilizes the spectral form of the Green's function to represent the pressure generated by an axisymmetric radiator as a single integral. However, the domain of integration is infinite and the integrand is weakly singular at the wavenumber k. In cylindrical coordinates, the King integral is given by

$$\widehat{p}(r,z;\omega )=\rho \omega {\int }_0^{\infty }\frac{\exp (-\mathit{jz}\sqrt{k^2-{\alpha }^2})}{\sqrt{k^2-{\alpha }^2}}\tilde{q}\left(\alpha \right)J_0\left(r\alpha \right)\alpha d\alpha ,$$ (2)

where q̃(α) is the Hankel transform of the apodization function q(σ) and J_n(z) is the Bessel function of the first kind of order n. In the case of the uniform piston, q̃(α) is proportional to aJ₁(αa)/α, reducing Eq. (2) to the classical King integral [see Eq. (7) in Ref. 1]. Unlike the 1/R singularity present in Eq. (1), Eq. (2) contains a weak singularity at α=k.¹⁷ Numerically, the integral is decomposed into two integrals ranging from [0,k) and (k, ∞) and a trigonometric and hyperbolic substitution is performed on each integral, respectively. The integration from [0,k) represents the propagating spectrum, whereas the integration from (k, ∞) represents the evanescent spectrum.

C. Annular superposition integral

The single-frequency pressure p̂_a(r, z; ω) generated by a circular piston a with spatially uniform velocity v₀ is given by the FNM¹⁴

$$\begin{array}{cc}\hfill {\widehat{p}}_a(r,z;\omega )& =\frac{\rho {\mathit{cav}}_0}{\pi }{\int }_0^{\pi }\frac{r\cos \psi -a}{r^2+a^2-2\mathit{ar}\cos \psi }\hfill \\ \hfill & \times (e^{-\mathit{jk}\sqrt{r^2+a^2+z^2-2\mathit{ar}\cos \psi }}-e^{-\mathit{jkz}})d\psi ,\hfill \end{array}$$ (3)

where ρc is the characteristic acoustic impedance of the (homogeneous) medium, v₀ is the piston velocity, and (r,z) are the observation coordinates in cylindrical coordinates. As suggested in Ref. 10, the pressure field p̂(r, z; ω) associated with the aperture function q(σ) can be synthesized by decomposing the circle of radius a into N concentric annuli where the ith annulus has inner radius (i−1)σ and outer radius iσ. After defining p_i = p̂_iΔσ(r, z; ω) and q_i=q(iΔσ) and a uniform spacing of annuli with Δσ=a/N, then the total pressure is written as

$$\widehat{p}(r,z;\omega )\approx \underset{i=1}{\overset{N-1}{\Sigma }}{p}_i(q_i-q_{i+1})+p_N{q}_N.$$ (4)

Taking q_N=0 (since the aperture function vanishes on the boundary), Eq. (4) can be written as a Riemann sum

$$\widehat{p}(r,z;\omega )\approx \underset{i=1}{\overset{N-1}{\Sigma }}-p_i\frac{q_{i+1}-q_i}{\Delta \sigma }\Delta \sigma .$$ (5)

Letting N→∞ and Δσ →0, the sum becomes an integral and the difference quotient becomes a derivative, yielding

$$\widehat{p}(r,z;\omega )=-{\int }_0^a{\widehat{p}}_{\sigma }(r,z;\omega )q^{\prime }\left(\sigma \right)d\sigma .$$ (6)

Inserting Eq. (3) into Eq. (6) yields the following double integral for the apodized pressure field:

$$\begin{array}{cc}\hfill \widehat{p}(r,z;\omega )& =-\frac{\rho {\mathit{cv}}_0}{\pi }{\int }_0^a{q}^{\prime }\left(\sigma \right)\sigma {\int }_0^{\pi }\frac{r\cos \psi -\sigma }{r^2+{\sigma }^2-2\sigma r\cos \psi }\hfill \\ \hfill & \times (e^{-\mathit{jk}\sqrt{r^2+{\sigma }^2+z^2-2\sigma r\cos \psi }}-e^{-\mathit{jkz}})d\psi d\sigma .\hfill \end{array}$$ (7)

Equation (7) provides the basis for the axisymmetric superposition method. By choosing the appropriate complex-valued aperture function q(σ), the acoustic field pressure p̂(r, z; ω) is specified for all observation points (r,z) in the acoustic half-space. Since the derivative q′(σ) appears in Eq. (7), the aperture function q(σ) must be at least weakly differentiable.

Physically, Eqs. (6) and (7) state that the total pressure generated by an apodized radiator consists of contributions from concentric annuli with uniform velocity. Note that Eq. (6) is valid for any pressure uniform pressure expression p̂_σ(r, z; ω), such as the impulse response integral.⁸ However, other single-integral solutions are defined piecewise over the computational domain, making the integration over σ intractable. The single integral expression developed for the fast nearfield method¹⁴ is ideal for those calculations due to rapid convergence in the nearfield region.

D. Pulsed circular radiator

The expression in Eq. (7) is also amenable to time-domain calculations of transient pressures generated by apodized circular pistons. The velocity distribution is assumed to be separable in radial coordinate σ and time t such that u(σ,t)=v(t)q(σ). For a pulse v(t) with a spectrum given by v̂(ω), the transient pressure field is recovered by weighting Eq. (7) by the pulse spectrum v̂(ω) and inverse Fourier transforming. These operations yield

$$\begin{array}{cc}\hfill p(r,z;t)& =-\frac{\rho c}{\pi }{\int }_0^a{q}^{\prime }\left(\sigma \right)\sigma {\int }_0^{\pi }\frac{r\cos \psi -a}{r^2+{\sigma }^2-2\sigma r\cos \psi }\hfill \\ \hfill & \times (v(t-{\tau }_1)-v(t-{\tau }_2))d\psi d\sigma ,\hfill \end{array}$$ (8)

where the delay times τ₁ and τ₂ are defined by

$${\tau }_1=\sqrt{r^2+z^2+{\sigma }^2-2r\sigma \cos \psi ∕c},$$ (9a)

$${\tau }_2=z∕c.$$ (9b)

III. APERTURE FUNCTIONS

In the following, double integral expressions are derived for the following aperture functions: uniform piston, smooth piston, and polynomial apodization. An expression for a pulsed, apodized piston is also derived.

A. Uniform piston

Note that for spatially uniform pressure, q(σ)=H(a−σ), where H(z) is the Heaviside function. Then the weak derivative is q′(σ)=−δ(σ−a), where δ(z) is the Dirac delta function. Inserting q′(σ)=−δ(σ−a) into Eq. (7) yields the original expression for pressure given by Eq. (3).

B. Smooth piston

A piston model proposed in Ref. 18 provides a smooth tapering of surface particle velocity near the surrounding baffle. This smooth piston assumes an aperture function given by

$$q\left(\sigma \right)=\{\begin{array}{cc}1\text{if}\sigma \le a\hfill & \hfill \\ \frac{{(1+\delta )}^2-{\sigma }^2∕a^2}{\delta (2+\delta )}\hfill & \text{if}a<\sigma \le a(1+\delta )\hfill \\ 0\text{otherwise},\hfill & \hfill \end{array}\phantom{\}}$$ (10)

where δ>0 is a unitless parameter that specifies a continuous transition region between piston-like motion and the rigid baffle. Note that the σ integral is evaluated over the thin semiannular region a(1+δ) ≤ σ ≤ a, which significantly reduces the computational complexity.

C. Polynomial apodization

Previous studies of piston radiators have employed polynomial apodization functions^2,19 to model the distribution of normal particle velocity across the face of the radiator. A general aperture function of the form

$$q\left(\sigma \right)=1-{(\sigma ∕a)}^n$$ (11)

is considered for σ<a. The uniform rigid piston is recovered by letting n→∞, while linear, quadratic, and quartic apodizations are obtained for n=1, n=2, and n=4, respectively. Evaluation of the on-axis pressure for 0<n<∞ shows a reduction in on-axis nulls that characterize the nearfield of circular pistons.

IV. NUMERICAL RESULTS

Examples of continuous wave and pulsed fields are computed using the apodization and phasing schemes described in Sec. II. All double integrals were evaluated via Gauss-Legendre quadrature.²⁰ Since the region of integration for each of the integral expressions is a half-disc of radius a, the number of quadrature points for the ith ψ or θ integral is chosen as proportional to the radial variable σ_i. Thus, the computational cost is reduced by roughly a factor of 2 relative to direct application of Gauss-Legendre quadrature. The King integral, given by Eq. (2), was evaluated using the substitutions given in Ref. 17. Both the propagating and evanescent integrals were integrated using Gauss-Legendre quadrature with an equal number of abscissas.

A fixed computational grid and sampling frequency (in the case of transient fields) is used in all field computations. In the following simulations, a piston of radius a=2.5λ=1.5 mm is driven at a center frequency of 2.5 MHz in a homogeneous medium with sound speed c=1.5 mm/μs. The scaling factor v₀ in Eq. (7) is taken to be unity. A fixed computational grid with 121 samples in the radial direction and 101 samples in the axial direction is employed, which corresponds to λ/4 spacing. The computational grid is axially offset by λ/4 in order to facilitate comparison to the Rayleigh-Sommerfeld integral in Sec. IV. The resulting fields are normalized with respect to the peak pressure magnitude.

A. Smooth piston fields

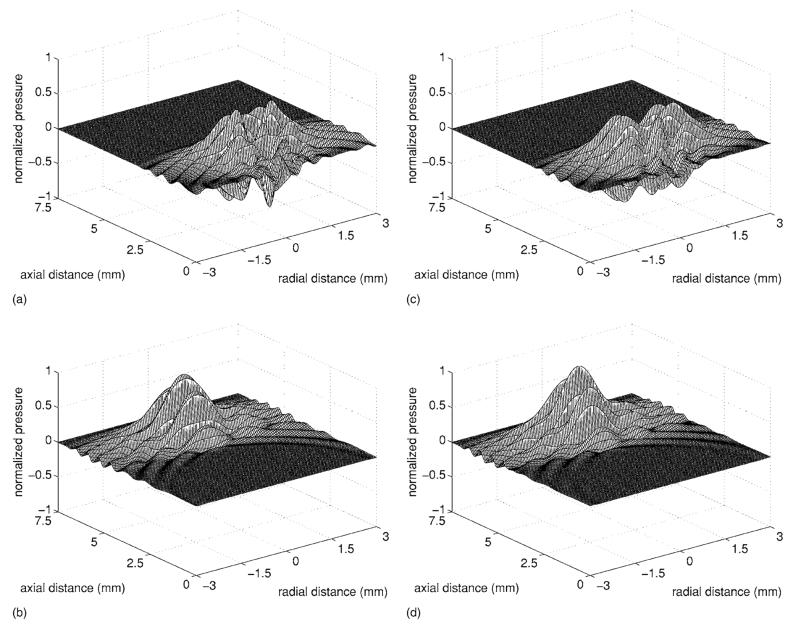
Figure 2 shows the normalized pressure fields produced by the “smooth” piston model given by Eq. (10). Figure 2(a) displays the pressure field associated with a relatively narrow transition region of δ=0.05, whereas Fig. 2(b) displays the pressure fields associated with a wider transition region of δ=0.30. Relative to the field in Fig. 2(a), the field in Fig. 2(b) contains less spatial variation resulting from less variation in the apodization function q(σ). The spatial bandwidth for each piston is quantified in Fig. 3, which displays the magnitude spectrum in the transverse plane z=0.9375 on a normalized decibel scale. Comparing Figs. 2(a) and 2(b), the δ=0.05 piston contains significantly more spectral information than the δ=0.3 piston due to a shorter transition band in the normal surface velocity. This wider spectrum correlates with the greater spatial variation depicted in Fig. 2(a).

FIG. 2.

Normalized pressure fields generated by “smooth” pistons modeled by Eq. (10). (a) The pressure produced by a piston with radius a=2.5λ with transition parameter δ=0.05, which closely resembles the field produced by a uniform piston. (b) The field generated by a piston with the same radius and δ=0.30.

FIG. 3.

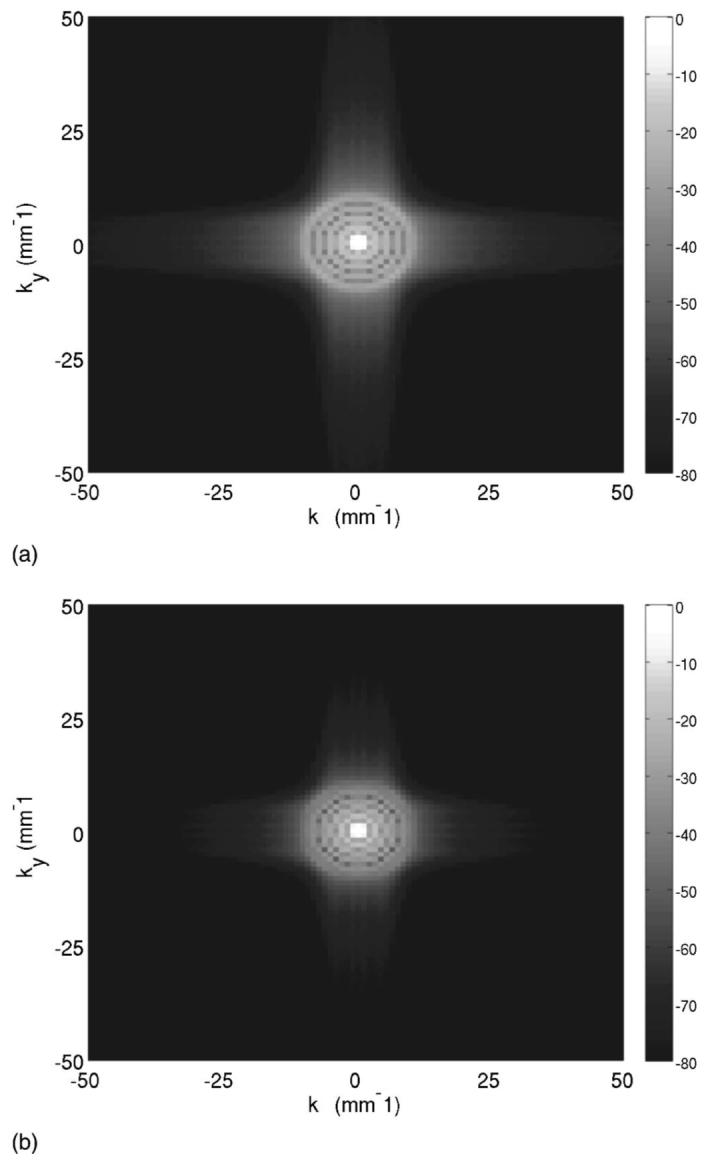
Normalized magnitude spectrum of the “smooth piston” pressure fields displayed in Fig. 2. In each panel, the nearfield pressure is calculated in a transverse plane at z=0.9375 mm via Eq. (10) followed by a two-dimensional Fourier transform. (a) The magnitude spectrum, displayed on a normalized decibel scale, for a smooth piston with δ=0.05. (b) The spectrum for a smooth piston with δ=0.30. Panel (b) contains significantly less spectral information than (a) due to the wider transition band.

B. Polynomial apodization

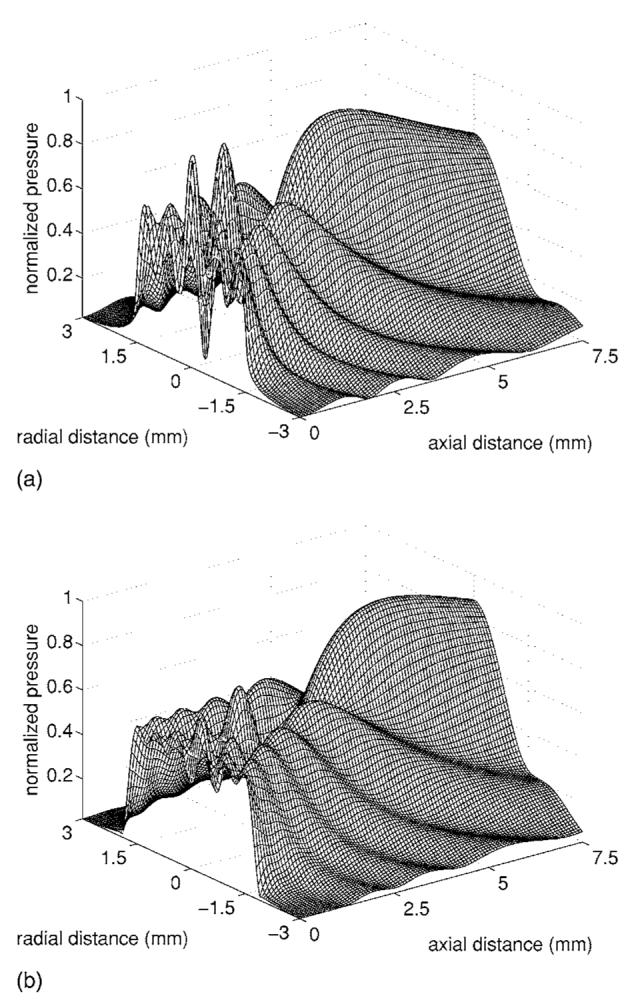
Pressure fields resulting from the polynomial apodization given by Eq. (11) are evaluated on a fixed computational grid for n=2 and n=4. The resulting normalized pressure fields are plotted in Fig. 4. Figure 4(a), displaying the effect of quadratic apodization, demonstrates the reduced spatial variation of the parabolic radiator compared to a uniform rigid piston with the same geometry (see Fig. 5 in Ref. 3). Spectral computations similar to those shown in Fig. 3 demonstrate the larger spatial bandwidth of the quartic apodization relative to the quadratic apodization. This greater bandwidth is observed qualitatively through the noticeable oscillations near the axial region in Fig. 4(b). These oscillations are produced by the rapid change in the apodization function near the piston boundary at r=a.

FIG. 4.

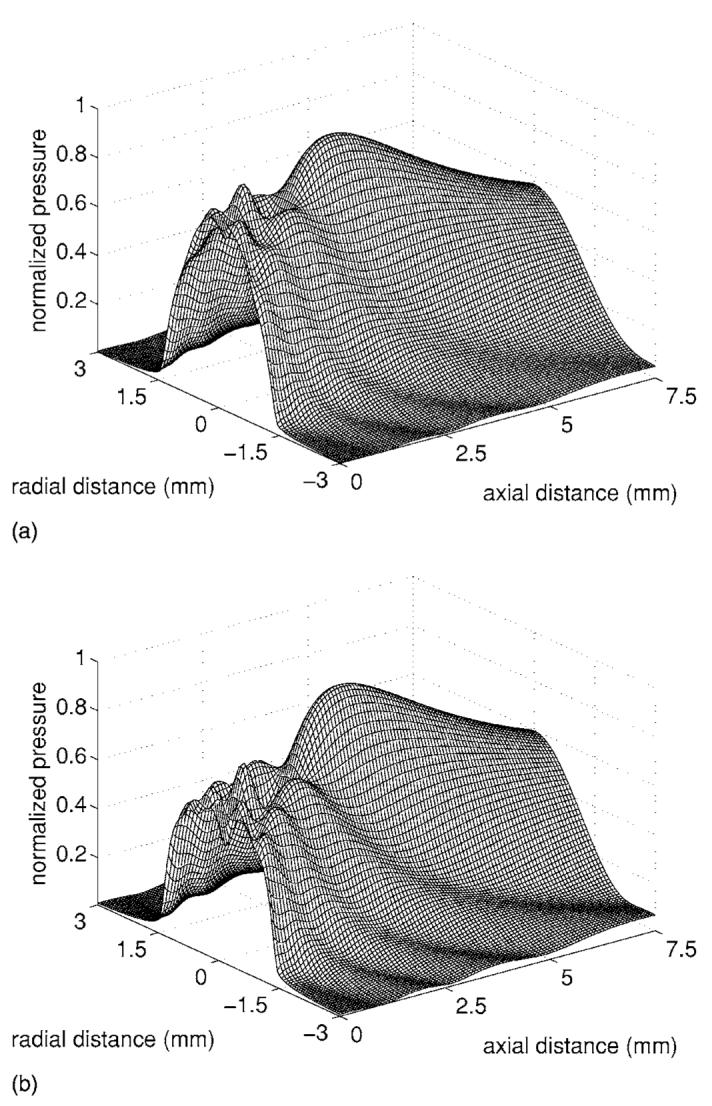
Reference pressure fields for polynomial apodization given by Eq. (11). (a) The effect of quadratic apodization (n=2). (b) Quartic apodization (n=4).

FIG. 5.

Pulsed fields generated by smooth pistons with the same parameters used in Fig. 2. The time evolution for smooth pistons with δ=0.3 and δ=0.05 are compared. (a) and (b) Normalized pressure fields corresponding to δ=0.05 at t=2.50 μs and t=5.00 μs, respectively. (c) and (d) Normalized pressure fields corresponding to δ=0.30 at t=2.50 μs and t=5.00 μs, respectively.

C. Pulsed fields

The time-domain pressure for the smoothed circular piston model was computed via Eqs. (8) and (10). The computational grid and piston parameters used in the continuous wave case were utilized in the pulsed case. Figure 5 displays the time evolution of the pulsed pressure fields associated with pistons having transition parameters δ=0.05 and δ=0.30. In both cases, a six-cycle Hanning-weighted tone burst with center frequency f₀=2.5 MHz models the excitation pulse v(t). Figures 5(a) and 5(c), which show, respectively, the normalized fields at t=2.50 μs for the δ=0.05 and δ=0.30 apodized pistons, exhibit a significant disparity between the two fields. In particular, the δ=0.05 piston exhibits an edge wave associated with the sharp change in surface velocity in the source plane; the edge wave for the δ=0.30 piston is not as pronounced due to the more gradual change in surface velocity. Figures 5(b) and 5(d) display the normalized fields at t=5.00 μs for δ=0.05 and δ=0.30; compared to Figs. 5(a) and 5(c), the two fields in Figs. 5(b) and 5(d) are very similar, indicating that the effects of spatial apodization are filtered out by space after a short propagation distance.

V. ERROR ANALYSIS

A. Reference field

The reference field was generated by applying a 20 000 point Gauss quadrature to the generalized King integral using quadratic apodization.⁴ This integration scheme resulted in a reference field that converged within 10⁻⁶ of machine precision.

B. Error metric

The spatial distribution of error is computed via the following metric:

$$\eta (r,z)=\frac{|\widehat{p}(r,z;\omega )-{\widehat{p}}_{\mathrm{ref}}(r,z;\omega )|}{{\max }_{r,z}\left|{\widehat{p}}_{\mathrm{ref}}(r,z;\omega )\right|}.$$ (12)

The peak error is then determined by taking the maximum of Eq. (12).

C. Error and time comparison

The annular superposition method, the point source method, and the generalized King integral were implemented in the C programming language and executed on a 3.0 GHz Pentium IV processor running red hat linux. The Bessel functions in the integrand of Eq. (2) were evaluated with the GNU Scientific Library.²¹ The annular superposition method, the point source method, and the generalized King integral subject to quadratic apodization are evaluated with varying numbers of quadrature points, and the computation times recorded at specified error levels. The resulting error and time analysis is summarized in Fig. 6. Figure 6(a) displays the number of quadrature points required to achieve a peak specified error, while Fig. 6(b) displays the associated computation times required for a specified error. Figures 6(a) and 6(b) demonstrate that the present superposition method converges significantly faster with respect to the point source approach and generalized King integral within the metric given by Eq. (12). For instance, at 10% peak specified error, the annular superposition method requires 20 quadrature points, while the point-source method requires 70 quadrature points and the generalized King integral requires 56 quadrature points. Comparing the computation times in Fig. 6(b), the superposition method requires 0.0486 s while the point-source method requires 0.1946 s at the 10% peak error level. Hence, the annular superposition method achieves a speed-up of a factor of 4 at the 10% error level. Although the generalized King integral requires less quadrature points than point-source to achieve 10% maximum error, the computation time associated with Eq. (2) is about twice as long relative to point-source calculations (0.3851 s vs 0.1946 s) due to evaluations of special functions.

FIG. 6.

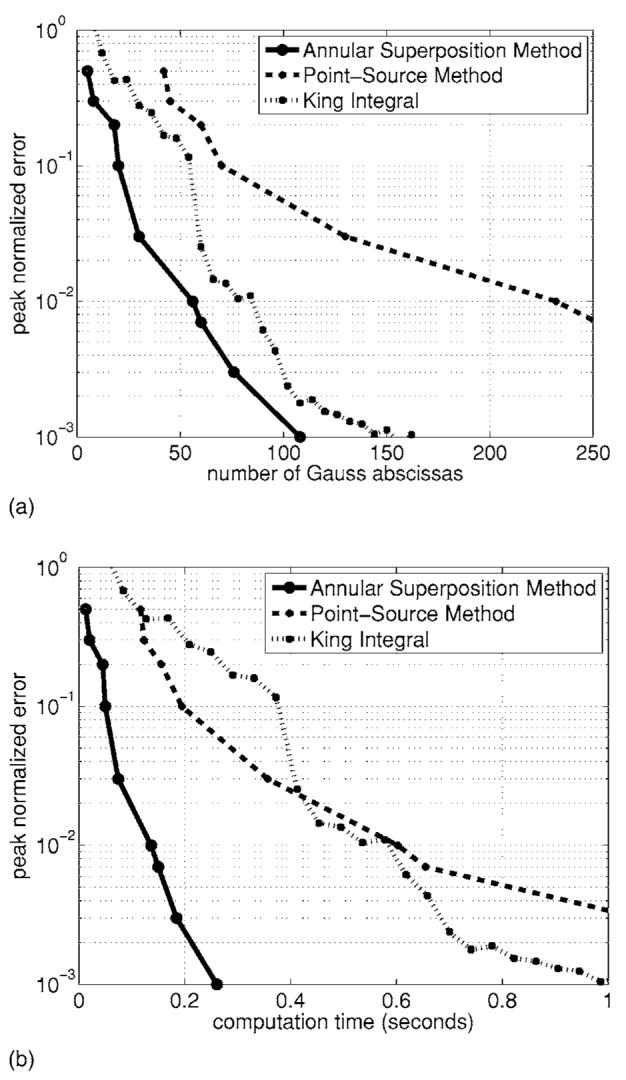
Number of Gauss abscissas vs specified peak error (a) and computation time vs specified peak error (b) for the annular superposition method, the Rayleigh-Sommerfeld integral, and the generalized King integral applied to a parabolic radiator. The annular superposition method achieves 10% peak error with the application of 20 abscissas, the Rayleigh-Sommerfeld approach requires 70 abscissas, and the generalized King integral requires 56 abscissas. Since the computation times are similar for each integral evaluated with the same number of abscissas, (b) demonstrates the present method's speed advantage compared to the Rayleigh-Sommerfeld approach and the generalized King integral at all error levels considered.

Similar speed-ups are observed at other specified peak error levels, with the speed-up increasing as the peak error decreases. At 1% peak error, the new method achieves a speed-up factor of 4.4 relative to the point-source approach and a speed-up factor of 3.7 relative to the generalized King integral.

VI. DISCUSSION

The farfield approximation is commonly employed to simplify cw and pulsed calculations of baffled radiators.²² Although the computational complexity of a problem is reduced by making this approximation, unacceptable error may be introduced if employed too close to the nearfield region. In the following, the farfield approximation applied to a parabolic radiator is analyzed.

The farfield directivity pattern for a parabolic radiator, obtained from the Hankel transform of Eq. (11) using n=2, is given by

$$D\left(\theta \right)=\frac{2J_2\left(\mathit{ka}\sin \theta \right)}{k^2{\sin }^2\theta },$$ (13)

where the angle θ=sin⁻¹(r/z). The farfield pressure field is then proportional to Eq. (13) multiplied by the free-space Green's function. The error due to the farfield approximation was then computed relative to the exact nearfield pressure. On-axis, the farfield error is less than 10% for all values of z>3.7a²/λ, where a²/λ is the farfield transition distance. The farfield error on-axis is less than 1% for all values of z>11.8a²/λ.

The farfield approximation introduces greater error for the uniform piston. The farfield error is less than 10% for all values of z>4.9a²/λ, while the error is less than 1% for all values of z> 15.7a²/λ. In all cases examined, the farfield error at a fixed axial location z is less for the parabolic radiator than the uniform radiator. Thus, the apodization of the piston reduces the effective size of the nearfield by reducing the spectral content of the wave field.

VII. CONCLUSION

A new analytical integral expression for the wave fields generated by axisymmetric radiators mounted in a rigid baffle has been derived. Integral expressions are derived for several common apodization models, including apodized transient excitations. The effect of apodization on the resulting wave field has been examined for both cw and transient excitations. Compared to the classical Rayleigh-Sommerfeld integral, this new approach converges faster with respect to the number of quadrature points by at least a factor of 4. A similar speed-up relative to the generalized King integral is observed. Unlike the generalized King integral, the annular superposition integral does not require the evaluation of special mathematical functions over an infinite range of integration. In short, the new method combines the ease of implementation of the point-source method with a more rapid convergence within the nearfield region of the radiator.