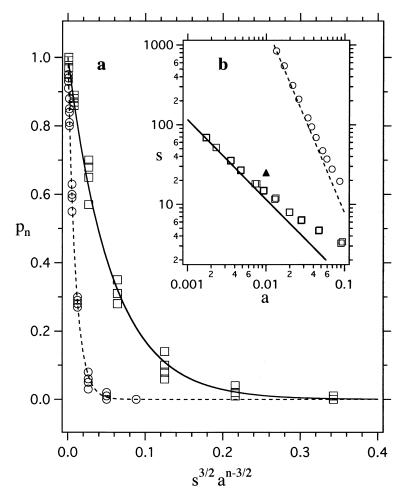
Figure 3.

(a) The probability p_n of not making all n contacts. The open symbols are the simulation results for n = 3 (squares) and n = 5 (circles). Vertical clusters of points represent maps with the same s and a but different random patterns of the attractive spots. For a given configuration of neighbors, a large sampling of orientation space was performed to search for orientations of the central particle in which all n contacts were made. This search was performed by combining random reorientations of the particle with small rotations about a randomly chosen axis to ensure a thorough sampling of all possible orientations. The probability p_n was calculated by counting the number of configurations of neighbors (of 100 randomly chosen ones) in which the central sphere did not make all n contacts. The theoretical results for n = 3 (solid line) and n = 5 (dashed line) also are shown (see Eq. 3). (b) The boundary for averaging the potential. The open symbols are the simulation results for n = 3 (squares) and n = 5 (circles). The values of s and a for each symbol are those that give p_n = 0.5. They were obtained by interpolating the simulation results for many different values of s and a that give p_n ≈ 0.5. Above the open symbols, the potential is averageable for the corresponding n; below, it is not. The lines are the results expected for n = 3 (solid) and n = 5 (dashed) from Eq. 3. The solid triangle corresponds to the values of s and a used in Fig. 2.