High numerical aperture tabletop soft x-ray diffraction microscopy with 70-nm resolution

Abstract

Light microscopy has greatly advanced our understanding of nature. The achievable resolution, however, is limited by optical wavelengths to ≈200 nm. By using imaging and labeling technologies, resolutions beyond the diffraction limit can be achieved for specialized specimens with techniques such as near-field scanning optical microscopy, stimulated emission depletion microscopy, and photoactivated localization microscopy. Here, we report a versatile soft x-ray diffraction microscope with 70- to 90-nm resolution by using two different tabletop coherent soft x-ray sources—a soft x-ray laser and a high-harmonic source. We also use field curvature correction that allows high numerical aperture imaging and near-diffraction-limited resolution of 1.5λ. A tabletop soft x-ray diffraction microscope should find broad applications in biology, nanoscience, and materials science because of its simple optical design, high resolution, large depth of field, 3D imaging capability, scalability to shorter wavelengths, and ultrafast temporal resolution.

X-ray crystallography is currently the primary method used to determine the 3D structure of materials and macromolecules. However, many nanostructures, materials, and biological specimens are noncrystalline and, hence, their structures are not accessible by x-ray crystallography. Visualizing these structures therefore requires a different approach. A very promising technique currently under rapid development is x-ray diffraction microscopy (or lensless imaging), in which the coherent x-ray diffraction pattern of a noncrystalline specimen is measured. In this technique, a sample is illuminated by coherent light, and the detailed scatter pattern is sampled at a rate higher than the Nyquist frequency. A computerized, iterative phase-retrieval algorithm replaces the imaging optics, thus making it possible to reconstruct an image of the sample. Since its first experimental demonstration by Miao et al. in 1999 (1), x-ray diffraction microscopy has been successfully applied to imaging of nanoscale materials and biological cells (2, 3) and to mapping of strain fields (4). Furthermore, in combination with x-ray free electron laser facilities, x-ray diffraction microscopy has the potential for single-shot imaging of single large macromolecules, without the need for crystallization (5–7). It also has several desirable qualities as an imaging technique, such as eliminating aberrations from optical elements (1)—in principle making it possible to achieve near-diffraction-limited resolution in the x-ray region and eliminating the need for precise positioning of the sample.

A bottleneck in the development of x-ray diffraction microscopy, however, has been the light-source requirements. Bright, fully coherent illumination is necessary, which generally has meant the use of large-scale, limited-access facilities such as x-ray lasers (8), third-generation synchrotron radiation sources (1), or x-ray free electron lasers (7). Although tabletop soft x-ray diffraction microscopy has recently been demonstrated by using a high-harmonic generation source (9), the retrieved spatial resolution of ≈214 nm was comparable to that of visible microscopy. Here, we demonstrate soft x-ray diffraction microscopy by using two complementary tabletop, coherent soft x-ray sources—a soft x-ray laser source producing high-energy (0.1–0.8 mJ) pulses at 47 nm (10–12) and a high-order harmonic generation source producing high-repetition-rate coherent beams at 29 nm (13–15). By using field curvature correction in the image reconstruction at high numerical aperture, we retrieve images with resolution as low as 70 nm by using setups that fit on a 4′ × 8′ optical table, including both the soft x-ray source and the microscope. This resolution compares well with recent experiments done at large-scale facilities and is very near (×1.5) the wavelength of the illuminating light itself. Because tabletop soft x-ray sources have already been demonstrated throughout the soft x-ray field, and new phase-matching techniques should increase their flux and coherence (16), the present work paves the way toward tabletop soft x-ray diffraction microscopy of materials and cryogenically fixed biological samples (17) with sub-10-nm resolution. Moreover, these results can also be extended to high temporal resolution by using femtosecond-duration, high-harmonic pulses (18). Therefore, compact coherent soft x-ray sources, when coupled with state-of-the-art imaging techniques, should find wide application in nanoscience, nanotechnology, and biological imaging.

Experiment

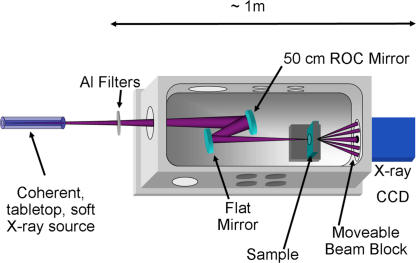
The experimental setup is shown in Fig. 1. Coherent beams from either a soft x-ray laser or a high-harmonic source are focused onto a sample by using a simple two-mirror relay arrangement. Light scattered from the object is then detected by using a CCD camera positioned a few centimeters from the sample. Thin-film filters are used to block unwanted longer-wavelength radiation. The soft x-ray laser source is based on fast electric-discharge excitation in a small-diameter capillary that creates a highly ionized neon-like argon plasma lasing at λ = 46.9 nm. It produces pulses of energy ≈0.2 mJ with ≈4.5 mrad divergence at a repetition rate of 1 Hz (10). This laser is based on high-gain amplification of spontaneous emission from the laser transition and, although it does not use a resonator, it nevertheless generates a beam with high spatial and temporal coherence. The longitudinal coherence length is determined by the Doppler-broadened linewidth of the laser transition at λ/Δλ ≈ 10⁴, corresponding to a coherence length of ≈500 μm. The degree of spatial coherence increases with the length of the plasma column and approaches full coherence for 36-cm-long capillaries (19). In this experiment, the laser output was spatially filtered to ensure good spatial coherence by using a 1.5-mm-diameter pinhole placed ≈1.5 m from the output of the laser, where the beam is ≈1.5 cm in diameter.

Fig. 1.

Setup of the tabletop soft x-ray diffraction microscope. A coherent soft x-ray beam is produced by high-harmonic generation or by spatially filtering the emission from a capillary discharge laser in an Ar-filled hollow waveguide. The beam is gently focused by a multilayer mirror pair onto the sample, and the diffraction pattern is collected on an x-ray CCD. A moveable beam block allows for brighter portions of the diffraction pattern to be blocked to avoid saturating the CCD when acquiring the highest angle diffracted light. ROC, radius of curvature.

The second tabletop source used for lensless imaging is based on phase-matched high-order harmonic up-conversion of intense femtosecond laser pulses. The output from a titanium-doped sapphire laser system producing 1.3-mJ pulses at a wavelength of 780 nm and with 25-fs duration and a repetition rate of 3 kHz, is focused into a 5-cm-long, fused silica capillary waveguide filled with Ar at a pressure of 65 torr. The waveguide has an inner diameter of 150 μm and produces a fully spatially coherent beam of approximately five phase-matched harmonics centered at the 27th order at a wavelength of 29 nm (13, 14, 18). A single harmonic order is then selected by the multilayer mirrors that focus the beam onto the sample, resulting in a linewidth of λ/Δλ ≈ 200.

The same microscope, shown in Fig. 1, was used to produce lensless images by using the two coherent soft x-ray sources. In the case of the soft x-ray laser, a single 100-nm-thick aluminum filter was used to block plasma emission at longer wavelengths. For the high-harmonic beams, two 200-nm-thick aluminum filters blocked the driving laser light at 780 nm. Two multilayer mirrors, one flat and one with a 50-cm radius of curvature, were used to gently focus the soft x-ray beams onto the sample. Different bilayer thicknesses and materials (Sc/Si for 46.9 nm or Mo/Si for 29 nm) were used to optimize reflection for the different wavelengths. The soft x-ray laser mirrors are 40% reflective at 46.9 nm, whereas the mirrors used to focus the high-harmonic beam are 28% reflective at 29 nm. The samples were held on a two-axis piezo stage, placed 2–4 cm from the camera, to optimally sample the diffraction pattern and to capture the highest possible angle of diffraction for the available flux. The diffraction patterns were captured on an x-ray CCD camera (Andor) with a pixel size of 13.5 μm in a 2048 × 2048 array. Beam blocks of varying sizes were used to block out the most intense portions of the diffraction pattern to increase the dynamic range of the recorded pattern beyond the dynamic range of the CCD.

Three basic requirements must be satisfied in lensless imaging. First, the object must be illuminated by a coherent wavefront; second, the object must be isolated; that is, it must be surrounded by a substantial region with no scatterers (which may be either opaque or transparent); and third, the scattered light must be collected with sufficient spatial resolution to oversample the diffraction pattern so that it is recorded at a frequency higher than the Nyquist frequency (20). This last condition is satisfied by setting the geometry of the imaging system so that the smallest diffraction speckle is sampled linearly by two or more CCD pixels. The linear oversampling ratio is given by 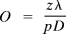, where z is the sample to CCD distance, λ is the wavelength, D is the sample diameter, and p is the pixel size of the CCD camera (20, 21). For both soft x-ray sources, the sample size was 7 μm. For the soft x-ray laser at 46.9 nm, the sample to CCD distance was 17 mm, giving an oversampling ratio of 8.5. For the high-harmonic source at 29 nm, the sample to CCD distance was 42 mm, giving an oversampling ratio of 13. The samples used for both sources were 7-μm-tall “waving stick girl” figures etched into a 100-nm-thick silicon nitride window. Because the silicon nitride is ≈4% transmissive to 29-nm photons, 200 nm of gold was electroplated on the sample used with the high-harmonic beam.

Results and Discussion

The coherent diffraction pattern from the first stick girl sample when illuminated by the soft x-ray laser for an exposure time of 300 shots (5 min at 1 Hz) is shown in Fig. 2a. To reduce noise originating from the laser source, the optical components, and the CCD detector, we applied a low-pass filter to the autocorrelation function obtained from a Fourier transform of the diffracted intensity. Because the electron density of the specimen is confined within the autocorrelation function region, any density outside that region is due to noise in the diffraction intensity. The low-pass filter applied had unity value across a region 1.5 times larger than the size of the autocorrelation function, and then gradually decreased to zero at the edges. After filtering, the diffraction intensity was binned by numerically integrating 3 × 3 pixels into 1 pixel. This binning not only increased the signal-to-noise ratio of the diffraction intensity, but also mitigated the requirement of beam coherence and expedited the image reconstruction. The binned diffraction intensity was then deconvolved to obtain the precise oversampled diffraction pattern (22).

Fig. 2.

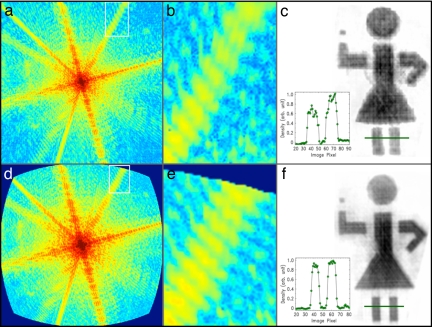
Curvature correction in high numerical aperture lensless imaging. (a and d) Coherent soft x-ray diffraction pattern at 47-nm wavelength (in transmission) before and after curvature correction (maximum momentum transfer of 0.166 nm⁻¹ at the edge of the CCD). (b and e) Magnified diffraction pattern at high diffraction angles showing the radial blurring near the upper-right edge in b, which is absent in e. (c and f) Reconstructed image of waving stick figure without and with curvature correction. The lower width and increased sharpness of the curvature-corrected stick-girl image can be seen in the lineouts shown in c and f Insets.

Our experimental setup was configured to enhance the spatial resolution by placing the detector as close to the sample as possible, which increases the numerical aperture of the microscope. In this mode of operation, the approximation of sin θ ≈ θ is no longer valid, and therefore the diffraction intensity on the planar CCD is significantly distorted at higher angles, as can be seen in Fig. 2 a and b. To remove the distortion, we interpolated the diffraction pattern from a plane onto a spherical surface. Fig. 2 d and e shows the curvature-corrected diffraction pattern, where the radial stretching and skew of the speckles near the edge of the diffraction pattern (corresponding to high diffracted angles) are clearly removed.

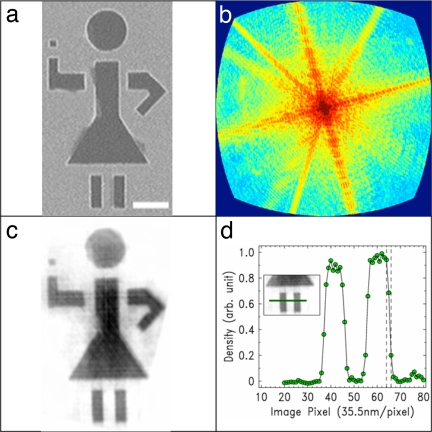
Because of the strong absorption of soft x-rays by the specimen, the diffraction pattern is noncentrosymmetrical, resulting in the complex electron density. Phase retrieval of the complex electron density was carried out by using the guided hybrid-input-output (GHIO) algorithm (see Methods) (21, 23). Fig. 2 c and f shows the magnitude of the reconstructed image before and after curvature correction, indicating that curvature correction indeed significantly improves the quality of the reconstruction. The lower width and increased sharpness of the curvature-corrected stick-girl image can be seen in the lineouts shown in Fig. 2 c and f Insets. The final reconstructed image is in excellent agreement with the SEM image shown in Fig. 3a. A lineout of the reconstructed image is shown in Fig. 3d, indicating a resolution of 71 nm. This resolution, at 1.5 λ, compares very well with other lensless imaging experiments done at large-scale facilities. Furthermore, our calculations have indicated that the resolution could reach the diffraction limit. The current resolution of 71 nm is limited by the size of the CCD detector, because the diffraction pattern in Fig. 2a was clearly cut off by the CCD edges. By using a larger CCD detector and this curvature-correction procedure, it should be possible to achieve diffraction-limit resolution by using a tabletop soft x-ray diffraction microscope.

Fig. 3.

Lensless imaging with coherent soft x-ray laser beams at 47 nm. (a) Reflection image of the waving stick-figure sample by using an SEM. (Scale bar, 1 μm.) (b) Coherent soft x-ray diffraction pattern (in transmission) after curvature correction (maximum momentum transfer of 0.166 nm⁻¹ at the edge of the CCD). (c) Reconstructed image with curvature correction. (d) Lineout of the image along the legs (Inset), verifying a resolution of 71 nm.

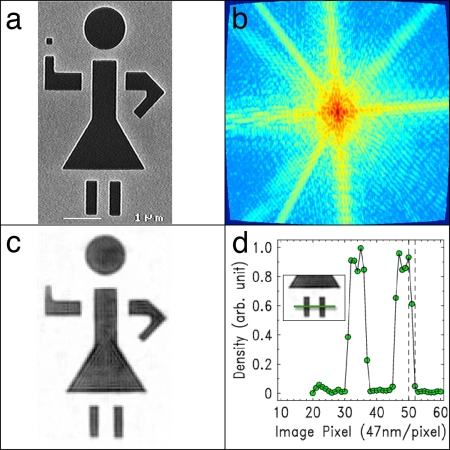
Fig. 4 summarizes the imaging results by using a high-harmonic source. A reflection image of the second stick girl sample using an SEM is shown in Fig. 4a, whereas Fig. 4b shows the curvature-corrected high dynamic range, soft x-ray diffraction pattern in transmission. Fig. 4c shows the reconstruction of the 7-μm stick figure, with a resolution of 94 nm verified in the lineout of Fig. 4d. This resolution is more than a factor of two better than resolutions reported by using either lensless or zone-plate microscopes based on high-harmonic sources. The reconstructed image has excellent fidelity with the SEM image, with the exception of missing the right hand. This is because of the finite resolution of the reconstruction, which is greater than the hand feature size, and possible incomplete etching of the substrate in this region.

Fig. 4.

Lensless imaging by using coherent high-harmonic beams at 29 nm. (a) Reflection image of the sample using an SEM. (Scale bar, 1 μm.) (b) Coherent soft x-ray diffraction pattern (in transmission) after curvature correction (maximum momentum transfer of 0.134 nm⁻¹ at the edge of the CCD). (c) Reconstructed image. (d) Lineout of the image along the legs (Inset), demonstrating a resolution of 94 nm.

Compared with Fig. 3c, Fig. 4c shows slightly more internal density fluctuations, which is likely due to the lower temporal coherence (higher spectral bandwidth) of the high-harmonic source compared with the soft x-ray laser. However, the region outside the sample boundary in Fig. 4c is much cleaner, which is attributed to the higher spatial coherence of the high-harmonic source. In addition, the higher spatial coherence of the high-harmonic source allows all of the output flux to be used, whereas the higher spectral bandwidth can support sub-10-fs pulse duration for dynamic imaging experiments. Furthermore, the bandwidth of the high-harmonic source can be engineered through a variety of coherent control techniques, which will make it possible to precisely determine the time–space resolution trade-off for such a source. In the case of the soft x-ray laser, an increase of the capillary length can simultaneously make the output essentially fully spatially coherent and significantly increase the pulse energy, making single-shot exposure possible. The complementary nature of the two laser sources will enable versatile tabletop soft x-ray diffraction microscopy with sub-10-nm resolution for imaging of a wide range of specimens in biology, materials science, and nanotechnology.

Future work can extend these results to higher spatial resolution by using shorter wavelengths and to dynamic imaging studies. Straightforward extension of the current work will allow imaging at the technologically important 13-nm wavelength by using both soft x-ray laser sources and high-harmonic sources. Higher-repetition-rate lasers, faster phase retrieval algorithms using parallel processors, and improved phase-matching techniques will improve the flux of the high-harmonic source and reduce data acquisition times, allowing extension of this work to materials and biological imaging throughout the soft x-ray region of the spectrum. At the same time, the short-pulse nature of the high-harmonic source will allow time-resolved imaging of dynamic processes with femtosecond time scales.

Methods

The Guided Hybrid-Input-Output Algorithm.

The GHIO algorithm begins with a number of independent reconstructions of each diffraction pattern by using random initial phase sets as initial input. Each reconstruction is iterated between real and reciprocal space by forward and inverse fast Fourier transformation. In real space, the sample density outside a support and the negative real or imaginary part of the density inside the support were slowly pushed close to zero. The support, a region within which the sample image is confined, is a rectangular shape with its size estimated from the linear oversampling ratio. In reciprocal space, the magnitude of the Fourier transform (i.e., square root of the diffraction intensity) remains unchanged, with the phase for each pixel updated in each iteration. This work used 20 initial reconstructions. After 3,000 iterations, 20 images were reconstructed, which was defined as the zeroth generation. An R-value was calculated for each image based on the difference between the measured and calculated magnitude of the Fourier transform. A seed image with the smallest R-value was selected for the reconstruction. By multiplying the seed with each of the 20 images and taking the square root of the product, a new set of 20 images was obtained, which was used as the initial inputs for the next generation. We repeated the procedure for the next generation, and after the seventh generation, the 20 reconstructed images became consistent. The final reconstruction was chosen from the average of the best three images with the smallest R-values.

Coherent Laser Source.

The soft x-ray laser source is based on fast electric-discharge excitation in a thin capillary that creates a highly ionized neon-like argon plasma lasing at λ = 46.9 nm. Lasing takes place on the 3s ¹P₁–3p ¹S₀ transition of neon-like Ar by exciting Ar gas in an alumina capillary (3.2-mm diameter, 27 cm long) with a current pulse of amplitude ≈24 kA with a 10% to 90% rise time of ≈40 ns (10–12). This laser occupies a footprint of 0.4 × 1 m². The fast current pulse is produced by discharging a cylindrical capacitor through a spark-gap switch connected in series with the capillary load. The current pulse rapidly compresses the plasma column to achieve a dense and hot plasma filament where a population inversion is created by electron impact excitation of the laser upper level and rapid radiative relaxation of the laser lower level. The capacitor employs a water dielectric that provides high-energy density and also cools the capillary. A continuous flow of Ar maintains a pressure of 490 mTorr in the capillary channel. A 1.5-mm-diameter pinhole placed ≈1.5 m from the output of the capillary, where the beam is ≈1.5 cm in diameter, was used to ensure fully spatially coherent output beams. We estimate (by using the van Cittert–Zernike theorem) that the beam has at least 85% fringe visibility at the edges of the pinhole.