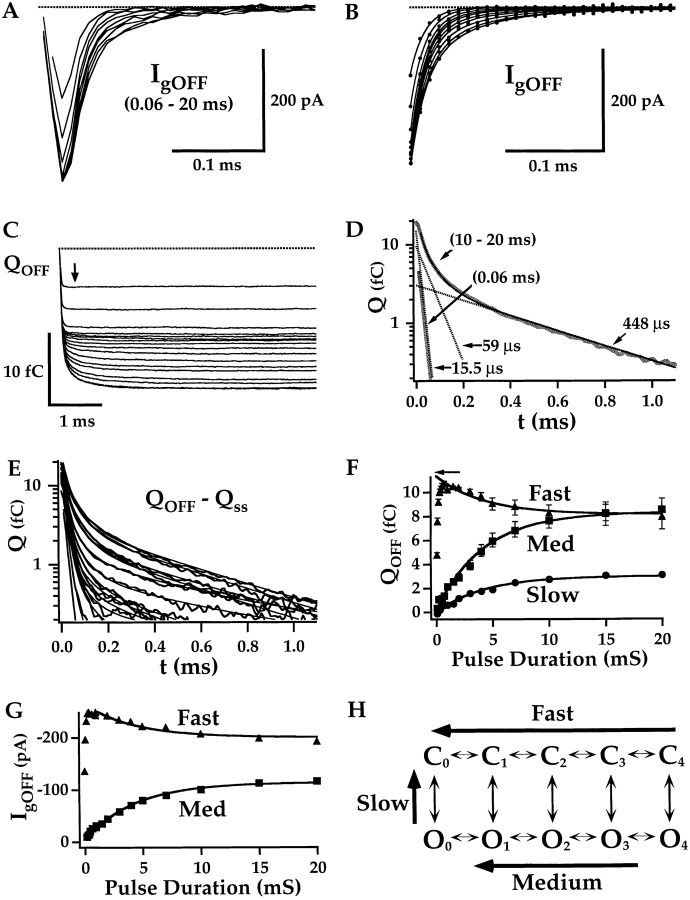
Figure 7.

Changes in OFF kinetics with channel activation. (A) A family of I _gOFF evoked at 2100 mV after pulses to +140 mV of 0.06–20 ms duration (from Fig. 6 A). Current amplitude is maximal after a 0.5-ms pulse, but I _gOFF decays more slowly as pulse duration increases. The baseline for each record is set to the mean current during an interval 4–5 ms after the pulse. (B) The decay of OFF currents are fit by double-exponential functions with τ_F = 15.5 μs and τ_M = 59 μs. (C) Q _OFF obtained by integrating I _gOFF from A achieves a steady state within 300 μs after a 0.06-ms pulse (arrow) but relaxes more slowly after longer pulses. (D) The kinetics of Q _OFF relaxation after a brief (0.06 ms) or prolonged (10–20 ms) pulses are compared by plotting Q _OFF–Q _ss on a semilog scale. Q _ss is the steady-state value of Q _OFF measured 3 ms after the pulse. The 0.06-ms trace is fit by a single-exponential function (τ_F = 15.5 μs). The 10–20-ms trace, representing an average of 10-, 15-, and 20-ms records, is fit by a triple exponential (solid line, τ_F = 15.5 μs, τ_M = 59 μs, τ_S = 448 μs) where the individual components are indicated by dashed lines. (E) A family of Q _OFF–Q _ss for the data in C. Traces are fit with triple exponential functions with the time constants determined from D. (F) Q _OFF component amplitudes from these fits are plotted versus pulse duration. The relaxation of all three components is fit by exponential functions (solid lines) with a time constant of 4.22 ms. Error bars represent the component amplitudes obtained when τ_M is changed by ±10% (with τ_F and τ_S held constant). The fast component of ON charge (Q _fast) is indicated by an arrow. (G) Fast and Medium I _gOFF component amplitudes determined from B are plotted versus pulse duration. Solid lines represent exponential fits with a time constant of 4.22 ms. (H) The allosteric model predicts three components of Q _OFF relaxation corresponding to the indicated transitions in the gating scheme.