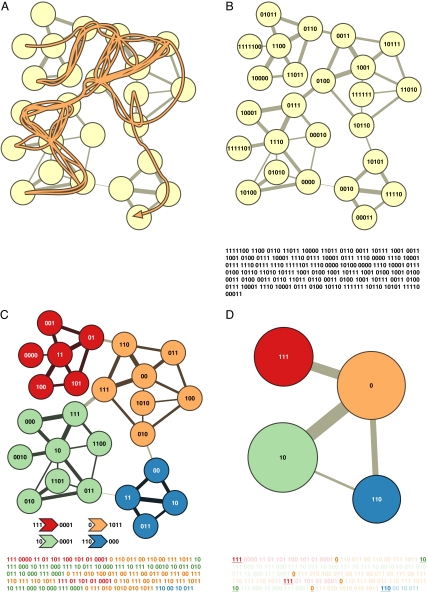
Fig. 1.

Detecting communities by compressing the description of information flows on networks. (A) We want to describe the trajectory of a random walk on the network such that important structures have unique names. The orange line shows one sample trajectory. (B) A basic approach is to give a unique name to every node in the network. The Huffman code illustrated here is an efficient way to do so. The 314 bits shown under the network describe the sample trajectory in A, starting with 1111100 for the first node on the walk in the upper left corner, 1100 for the second node, etc., and ending with 00011 for the last node on the walk in the lower right corner. (C) A two-level description of the random walk, in which major clusters receive unique names, but the names of nodes within clusters are reused, yields on average a 32% shorter description for this network. The codes naming the modules and the codes used to indicate an exit from each module are shown to the left and the right of the arrows under the network, respectively. Using this code, we can describe the walk in A by the 243 bits shown under the network in C. The first three bits 111 indicate that the walk begins in the red module, the code 0000 specifies the first node on the walk, etc. (D) Reporting only the module names, and not the locations within the modules, provides an efficient coarse graining of the network.