Figure 5. Dimensionality reduction.

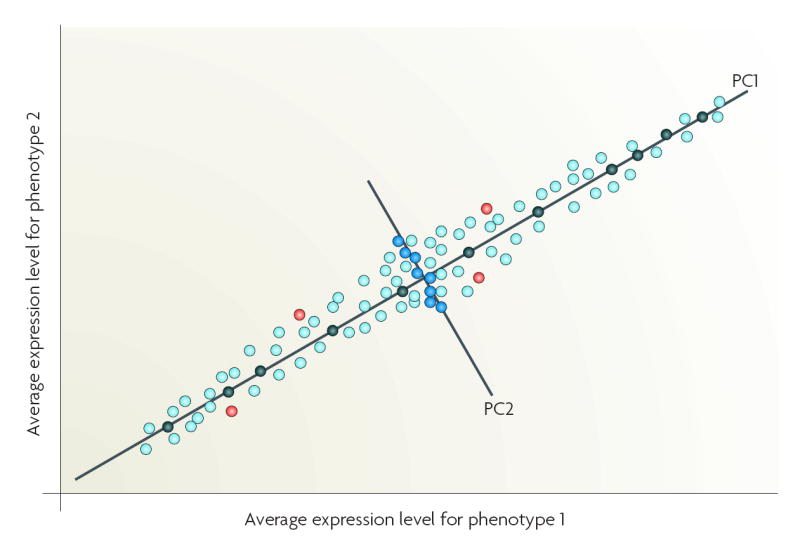
A practical implication of the curse of dimensionality is that, when confronted with a limited training sample, an investigator will select a small number of informative features (variables or genes). A supervised method can select these features (reduce dimensionality), where the most useful subset of features (genes or proteins) is selected on the basis of the classification performance of the features. The crucial issue is the choice of a criterion function. Commonly used criteria are the classification error and joint likelihood of a gene subset, but such criteria cannot be reliably estimated when data dimensionality is high. One strategy is to apply bootstrap re-sampling to improve the reliability of the model parameter estimates. Most approaches use relatively simple criterion functions to control the magnitude of the estimation variance. An ensemble approach can be derived, as multiple algorithms can be applied to the same data with embedded multiple runs (different initializations, parameter settings) using bootstrap samples and leave-one-out cross-validation. Stability analysis can then be used to assess and select the converged solutions¹¹⁴. Unsupervised methods such as principal component analysis (PCA) can transform the original features into new features (principal components (PC)), each PC representing a linear combination of the original features¹¹⁷. PCA reduces input dimensionality by providing a subset of components that captures most of the information in the original data¹¹⁸. For example, those genes that are highly correlated with the most informative PCs could be selected as classifier inputs, rather than a large dimension of original variables containing redundant features¹¹⁹,¹²⁰. Non-linear PCA, such as kernel PCA can also be used for dimensionality reduction but adds the capability, through kernel-based feature spaces, to look for non-linear combinations of the input variables³⁶. PCA is useful for classification studies but is potentially problematic for molecular signalling studies. If PC1 is used to identify genes that are differentially expressed between phenotypes 1 and 2, then genes that are strongly associated with PC1 (black circles) would be selected. If both PC1 and PC2 are used, then genes strongly associated with PC1 (black circles) and PC2 (blue circles) would be selected. Some genes could be differentially expressed but weakly associated with the top two PCs (PC1, PC2) and so not selected (red circles). As their rejection is not based on biological function(s), key mechanistic information could be lost.