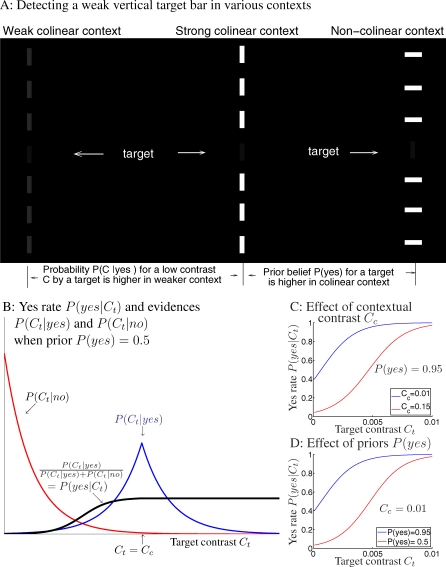
Figure 2. Bayesian Inference for Target Perception.

(A) Schematics of perceiving a weak vertical target bar in three different contexts. Colinear contexts give a higher prior belief P(yes) of the target present, as it could be grouped with the context. Higher contextual contrast C_c makes a low contrast input C_t at the would-be target location seem less likely to be caused by a target rather than noise, since observers expect a target to evoke a contrast similar to C_c, i.e., P(C_t | yes) peaks at C_t ≈ C_c, and P(C_t | yes) ≈ 0 if C_t ≪ C_c; see (B).

(B) the probability P(yes | C_t) of “yes” response depends on the ratio between the evidences P(C_t | yes) and P(C_t | no) for target present and absent, respectively, when the prior belief P(yes) = 0.5 is unbiased. This ratio should be multiplied by P(yes)/(1 − P(yes)) in general. Note that probability distributions P(C_t | yes) and P(C_t | no) peak at C_t = C_c and C_t = 0, respectively.

(C,D) Effects of the contextual contrast C_c (C) and of the prior P(yes) (D) by the Bayesian model. In (C) and (D), all curves have model parameters k = 2 and σ_n = 0.0015, the two red curves are identical, with P(yes) = 0.95 and C_c = 0.01. Comparing (C) and (D), a higher contextual contrast C_c has a similar effect as a lower prior P(yes).