Adsorption and elution characteristics of nucleic acids on silica surfaces and their use in designing a miniaturized purification unit

Abstract

We report nucleic acid (NA) adsorption isotherms and elution profiles for silica surfaces and use these to design a miniaturized NA purification unit based on solid-phase extraction with silica beads. The procedure is based on a pressure drop equation for flow through a packed bed and allows estimation of key design parameters such as channel dimensions, liquid flow rates, sample volume and amount of silica needed. The usefulness of this design procedure is shown by applying it to a column-based NA purification device for influenza detection for a case study of Madin-Darby canine kidney (MDCK) cells infected with influenza A virus.

Recently, microfluidic chips have been developed with the capability to perform quantitative polymerase chain reaction (PCR) assays using nanoliter-scale quantities of reagents and sample materials [1-2]. Due to the sensitivity of PCR to impurities, relatively pure nucleic acid (NA) is required as a starting template [3]. Typically, NA purification from clinical samples is accomplished using commercial bench-scale purification kits. These procedures are relatively slow, require large volumes on the order of a milliliter and are normally carried out in traditional lab facilities. These factors limit the portability of PCR microchips.

The development of a portable device or microchip capable of purifying NAs from a clinical sample would solve this problem. An integrated chip that is able to purify and concentrate NAs and subsequently amplify a specified target with PCR could provide on-the-spot detection of bacterial or viral pathogens. Since the chip would be a closed system, sample contamination between purification and PCR amplification steps would be ameliorated. The entire reaction could be completed in a rapid and efficient manner due to the minute quantities of starting material and reagents required [4-5].

The binding of NAs in the presence of a chaotropic salt solution, such as guanidinium thiocyanate, to the surface of silica particles is well known [6-7] and is the basis of many bench-scale NA purification procedures. While these bench-scale solid-phase purification methods typically use centrifugation to drive flow over the silica particles, it has been demonstrated that it is possible to adapt this NA purification method to micron-scale formats by using pressure-driven flow [8-11]. The solid-phase silica-based method yields pure NA that is free from any PCR inhibitors [8].

In this report, we develop a procedure for designing a NA purification microcolumn based on solid-phase-extraction using silica particles. A set of experiments required in order to determine numerical parameters needed for design purposes is also presented. These experiments: i) specify NA adsorption isotherms for several different chaotropic salts, ii) characterize the NA elution profile from a miniaturized capillary-like micro-solid-phase extraction (μSPE) device developed based on the work of Tian et al. [11] and iii) determine the relative amounts of pathogenic NA and total NA in a biological sample.

Materials and methods

Silica preparation

Irregularly shaped silica particles 0.5-10 μm in diameter and 6.9 m²/g surface area per unit mass (Sigma-Aldrich, St. Louis, MO) were cleaned with 1 mL of 3 M HCl in a 1.5 mL microtube by vortexing and subsequent centrifugation to remove the acidic supernatant. The particles were rinsed with water and allowed to dry at 100°C for 3 h. Cleaned particles were stored in a PCR-ready 1.5 mL microtube.

λ-DNA preparation

λ-DNA was purchased from Invitrogen (Carlsbad, CA). Prior to use, the λ-DNA solution was therefore heated to 65°C for 10 min and placed in a −20°C freezer for 5 min to restore all DNA to its linear form.

Cloned influenza RNA

The HA1 gene from influenza type A RNA was reverse-transcribed (RT), and PCR-amplified with primers complementary to the HA1 protein-encoding region. The PCR-amplified product (987 bp) was cloned into the pGEM-T Easy plasmid vector obtained from Promega (Madison, WI). Synthetic viral RNAs were generated using an in vitro transcription system (Riboprobe, Promega Inc.), as directed by the manufacturer, from Ncol-restriction digested plasmid DNA. The RNA transcribed by Sp6 RNA polymerase transcribed RNA was treated with RQ1 RNAse-free DNAse (Promega Inc.) at 37°C for 15 min. It was then extracted in phenol/chloroform, ethanol precipitated, and re-suspended in deionized water to 300 ng μL⁻¹.

Chaotropic salt solutions

Guanidinium hydrochloride (GuHCl), guanidinium thiocyanate (GuSCN), sodium chloride (NaCl) and sodium perchlorate (NaClO₄) solutions obtained from Fisher Scientific (Fairlawn, NJ) were prepared with molecular biology grade (MBG) water obtained from Eppendorf (Hamburg, Germany). Salt solutions were buffered with 50 mM Tris-HCl. Solution pH was titrated with 0.1 M HCl or NaOH.

Commercial NA purification kits

The QIAamp DNA Mini kit and the RNeasy Mini kit were purchased from Qiagen (Valencia, CA). Concentrated buffer solutions were prepared as instructed.

Micro-solid-phase extraction (μSPE) device

Glass fibers were removed from glass fiber filter circles (Fisher) with a pore diameter of 1.6 μm. Polyethylene tubing (i.d. 0.38 mm, o.d. 1.09 mm) was obtained from BD Biosciences (Franklin Lakes, NJ). Fused silica capillaries (50 μm i.d.) were obtained from Polymicro (Phoenix, AZ). A 100 μL gastight syringe was obtained from Hamilton (Reno, NV). Design of this device is as per Tian et al. [11] and is illustrated in Fig. 1. This device is essentially a packed bed of silica particles that are immobilized with glass fiber frits and interfaced with polyethylene tubing and silica capillaries.

Fig. 1.

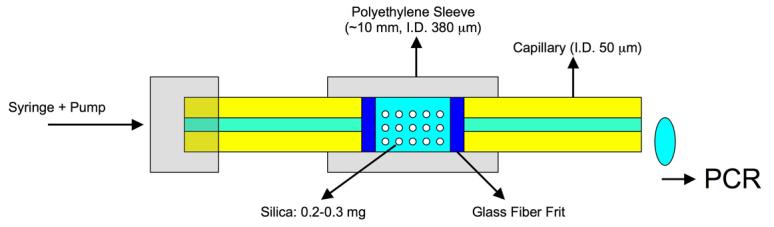
Schematic diagram of the micro-solid-phase extraction (μSPE) device designed as per ref [10].

Real-time PCR

TaqMan universal PCR mastermix, TaqMan universal RT-PCR mastermix, PCR primers and Taq MGB probes were obtained from Applied Biosystems (Foster City, CA). All PCR reactions were run on an ABI Prism 7000. Quantitative detection of λ-DNA was determined with primers (forward: 5'-CAT CAA AGC CAT GAA CAA AGC A-3'; reverse: 5'-TCA GCA ACC CCG GTA TCA G-3') and probe: 6FAM-CCG CGC TGG ATG A-MGBNFQ. Quantitative detection of the HA1 gene of influenza A/LosAngeles/01/87 was determined with primers (forward: 5'-TCT ATT GGG AGA CCC TCA TTG TG-3'; reverse: 5'-CGT TCA ACA AAA AGG TCC CAT T-3') and probe: 6FAM - TGG CTT CCA AAA TGA – MGBNFQ. Primers and probes for λ-DNA and A/LosAngeles/01/87 influenza RNA were designed using Primer Express software (Applied Biosystems). Probes were selected with no G's at the 5' end and a melting temperature of ca. 69°C. For λ-DNA, a 50 μL PCR was performed using 5 μL of DNA containing sample, 25 μL of TaqMan universal PCR master mix (Applied Biosystems), 2.25 μL of each 900 nM primer, 0.625 μL of the 250 nM probe and 14.875 μL of MBG water. For influenza RNA, a 50 μL PCR was performed using 5 μL of RNA, 25 μL of TaqMan one-step RT-PCR master mix (Applied Biosystems), 1.25 μL of RNase inhibitor mix, 2.25 μL of each 900 nM primer, 0.625 μL of the 250 nM probe and 13.625 μL of MBG water. The ABI Prism 7000 was run under the following reaction conditions: i) for λ-DNA, the reaction was held at 95°C for 10 min for uracil-N-glycosylase (UNG) inactivation and was amplified by two-step cycles (15 s at 95°C, 1 min at 60°C), ii) for influenza RNA, the reaction was held at 48°C for 30 min in order to complete reverse transcription, and then was held at 95°C for 10 min for UNG inactivation and was amplified by two-step cycles (15 s at 95°C, 1 min at 60°C).

MDCK cells and influenza A virus

MDCK cells were obtained from the American Type Culture Collection. Cellular passaging media consisted of 450 mL Dulbecco's Modified Eagle's Medium obtained from Biowhittaker (Walkersville, MD), 0.5 mL gentamicin sulfate (50 mg mL⁻¹), 10 mL of 2 mM L-glutamine and 50 mL of inactivated fetal bovine serum obtained from Fisher. Egg-passaged A/LosAngeles/01/87, a H3N2 strain of influenza A, was used to infect the cultured MDCK cells. Virus passaging media consisted of 100 mL Dulbecco's Modified Eagle's Medium, 0.1 mL gentamicin sulfate (50 mg mL⁻¹), 2 mL of 2 mM L-glutamine and 0.2 mL of TPCK trypsin obtained from Worthington Biochemicals (Lakewood, NJ).

UV spectrophotometry

NA concentration was determined by measuring the absorbance of the solution at 260 nm using a Hewlett-Packard 8453 spectrophotometer. NA concentration was calculated based on absorbance at 260 nm with the baseline taken as the absorbance at 320 nm.

Nucleic acid adsorption measurements

Adsorption measurements were obtained with the procedure outlined by Melzak et al. [13]. For samples containing chaotropic salts with high absorbances at a wavelength of 260 nm, the aliquot was processed with the QIAamp kit prior to UV measurement. In addition to UV spectrophotometry, samples containing low NA concentrations were measured with real-time PCR, which required processing with the QIAamp kit prior to measurement to remove the salt ions, which interfere with PCR.

Purification of NA by micro-solid-phase extraction

Solutions were premixed and pumped through the μSPE device using a S100 syringe pump obtained from KD Scientific (Holliston, MA). The purification procedure consisted of: i) loading the NA onto the silica particles with the loading buffer, ii) washing the silica particles to remove the chaotropic salt and any other contaminants and iii) eluting the adsorbed NA. Either λ-DNA or influenza viral RNA solution was mixed in a 1 to 10 volumetric ratio with 6 M GuSCN (pH 8.0), with the final concentration ranging from 0.2 to 1 ng μL⁻¹. In the loading step, 10 μL of this GuSCN solution containing NA was pushed through the device. For the washing step, 10 μL of 80% isopropanol or 10 μL of ethanol was used for DNA or RNA, respectively. The NA was eluted with 10 to 20 μL of MBG water.

μSPE device measurements

NA elution profiles were determined by collecting droplets from the μSPE device during the elution step. To generate high-resolution NA elution profiles, droplets of ca. 1 μL each were collected for NA concentration measurement with real-time PCR. The droplets were collected in 1.5 mL microtubes containing 10 μL of water. The droplet volume was determined by a mass difference measurement of the microtube with and without the added droplet.

Preparation of infected MDCK cells

Influenza virus was passaged in MDCK cell lines in order to obtain infected cells in the presence of actively growing virus. A 95% confluent monolayer of MDCK cells was infected with influenza A virus and incubated for 5 days at 37°C and 5% CO₂. After 5 days, a cytopathic effect was observed and the cells were harvested in MDCK viral infection media.

Results and discussion

Experimental overview

The experimental results presented in this section provide quantitative data needed for the design of a NA purification column. These experiments include: i) determining NA adsorption isotherms for different chaotropic salts, ii) determining NA elution profiles from a high-aspect ratio micron-scale device and iii) determining the relative amounts of viral NA and total NA in a biological sample consisting of MDCK cells infected with influenza A virus, resembling what would be obtained from a patient.

NA adsorption isotherms were generated to determine whether significant differences in NA adsorption to silica exist for different salts. The adsorption isotherms also provided quantitative data on the amount of NA that could be adsorbed by a specific surface area of silica. These data are essential to the design procedure discussed later because they determine a lower bound on the amount of silica that must be included in a microfabricated device. Moreover, because the adsorption isotherm is a thermodynamic property determined by equilibrium between surface and solution, these data are independent of extensive properties of the silica, particularly the bead size. Thus, their determination here generally addresses the design of any purification device involving silica beads, NAs and the salt buffer solutions of this study.

The elution behavior of NAs desorbing from silica particles in a μSPE device designed as per Tian et al. [11] was established to determine the feasibility of concentrating NA to perform a microliter-scale PCR reaction. High-resolution elution profiles were generated to determine the volume of water necessary to recover a specific amount of NA and which volume fractions contained the largest amount of NA.

To design a device for a particular pathogen, the relative amounts of NA in a sample, both pathogenic and non-pathogenic, need to be determined in order to estimate how much sample is needed to provide sufficient NA for an assay. A case study of Madin-Darby canine kidney (MDCK) cells infected with influenza A virus is presented. The experimental parameters relating to NA amounts needed for the design are obtained for this case study.

NA adsorption isotherms

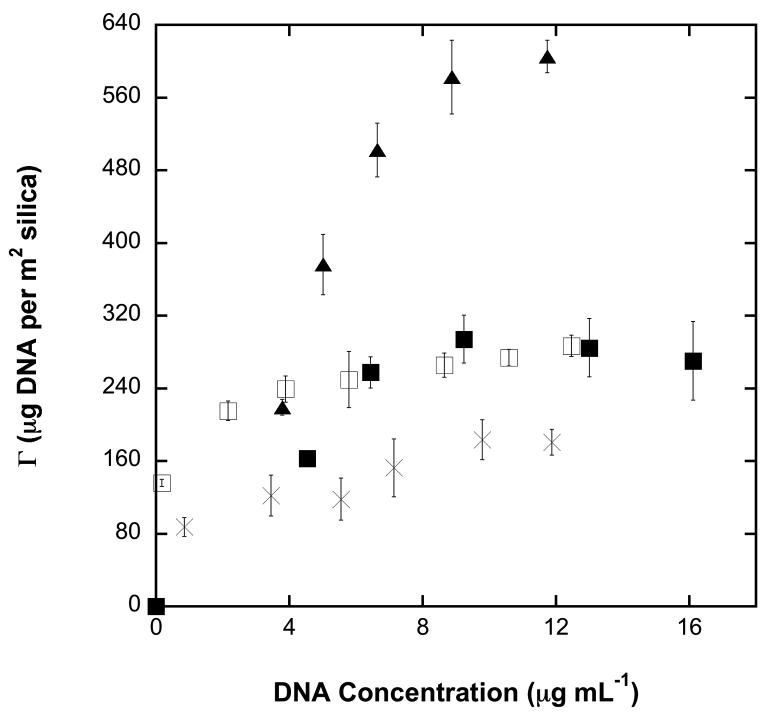
In developing a solid-phase NA purification device, the most efficient chaotropic salt is desired for inducing maximum adsorption of NA to the silica surface. To establish this, Figure 2 shows adsorption isotherms for linearized λ-DNA (48.5 kbp) in solutions of four potential agents: GuHCl, GuSCN, NaCl and NaClO₄. A salt concentration of 3 M was chosen for direct comparison between the salts since it is close to the solubility limit of NaCl in water. Under adsorption conditions of 3 M salt concentration and a pH of 8.0, GuSCN was found to have the highest adsorption plateau, saturating at ca. 600 μg m⁻². As expected, the salt NaCl has the lowest adsorption plateau, saturating at ca. 180 μg m⁻².

Fig. 2.

Adsorption isotherms for NaCl (crosses), NaClO₄ (open squares), GuHCl (filled squares) and GuSCN (filled triangles) at a concentration of 3 M and pH 8.0. Error bars are calculated for an average of four measurements and indicate standard error.

The good correspondence between the measured adsorption isotherm for NA in 3M NaClO₄ and the measurements of ref [13] for different silica properties supports our earlier discussion that adsorption isotherm data can be applied to sources of nonporous silica having different mean particle size.

GuSCN is not only the most efficient chaotropic salt with which to run the adsorption, due to its high NA saturation value on the silica surface. Moveover, this salt is also known to efficiently lyse cells and denature proteins [6], eliminating the need for the addition of denaturing enzymes.

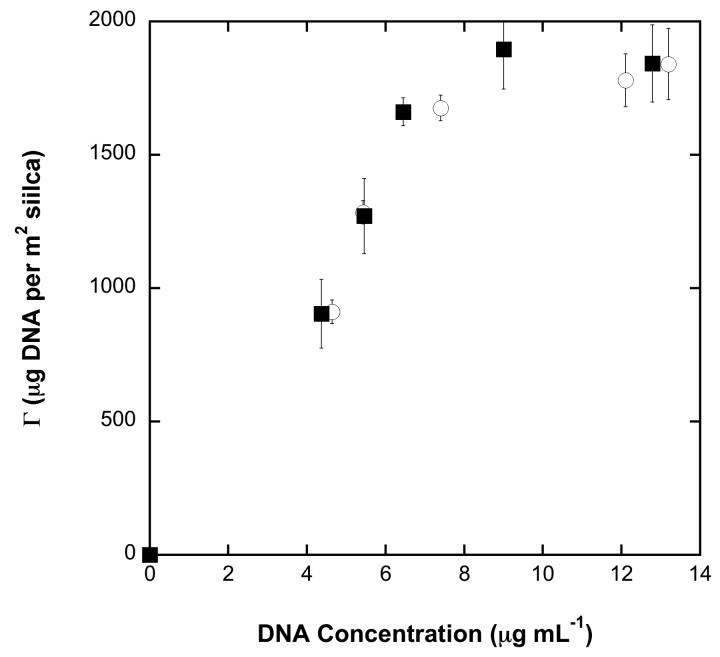
Increasing salt concentration and lowering solution pH generally increases NA surface saturation values [13]. From a design perspective, it would useful to determine the maximum amount of NA that can be adsorbed to the silica surface under ideal process conditions. Figure 3 displays adsorption isotherms for 6 M GuSCN at pH values of 6.0 and 8.0. Within standard error the adsorption isotherms behave nearly identically with both saturating at ca. 1850 μg m⁻².

Fig. 3.

Adsorption isotherms for 6 M GuSCN at pH 6.0 (filled squares) and pH 8.0 (open circles).

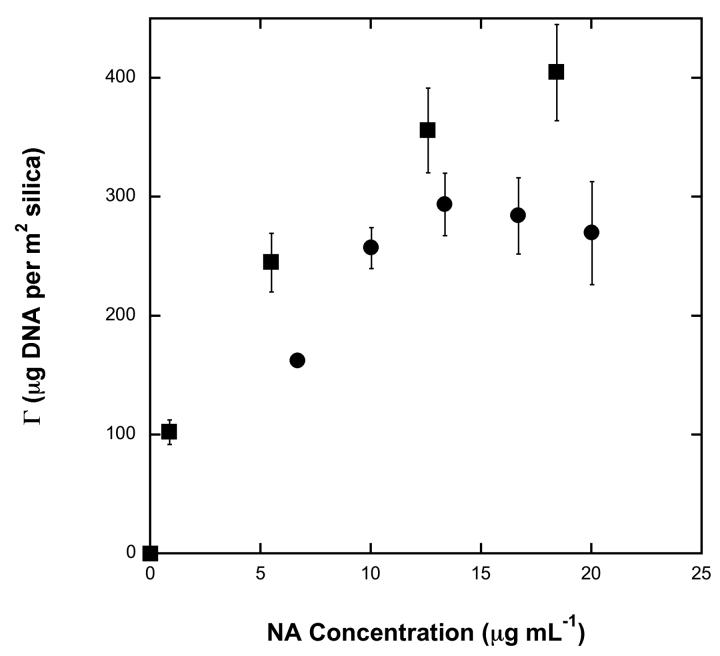
The target NA for many dangerous pathogens such as influenza is RNA. RNA is less stable than DNA and easily degraded by many enzymes in the environment, making it more difficult to work with than DNA. RNA adsorption plateau values in various chaotropic salt solutions need to be determined to design a purification microchip that targets RNA pathogens. To the best of our knowledge, no study in the literature has addressed RNA adsorption isotherms. Figure 4 displays our adsorption isotherms for λ-DNA and total human RNA in 3 M GuHCl with a pH of 8.0. RNA appears to adsorb more efficiently to silica than does DNA with similar adsorption isotherm behavior.

Fig. 4.

Adsorption isotherms for λ-DNA (filled circles) and total human RNA (filled squares) in 3 M GuHCl at pH 8.0. The error bars for λ-DNA represent standard error for n = 4. The error bars for total human RNA represent an estimated error of 10 percent.

Micro-solid-phase extraction of NAs and elution profiles

Due to the minute quantities of reagents and starting materials required by a real-time PCR microchip [1-2], the volume of elutant necessary to recover sufficient NA for PCR amplification needs to be determined. Measurement of NA desorption from silica particles in a μSPE device would help establish the feasibility of concentrating the NA sufficiently to perform a microliter-scale PCR reaction and determine which volume fractions contain the largest amounts of NA.

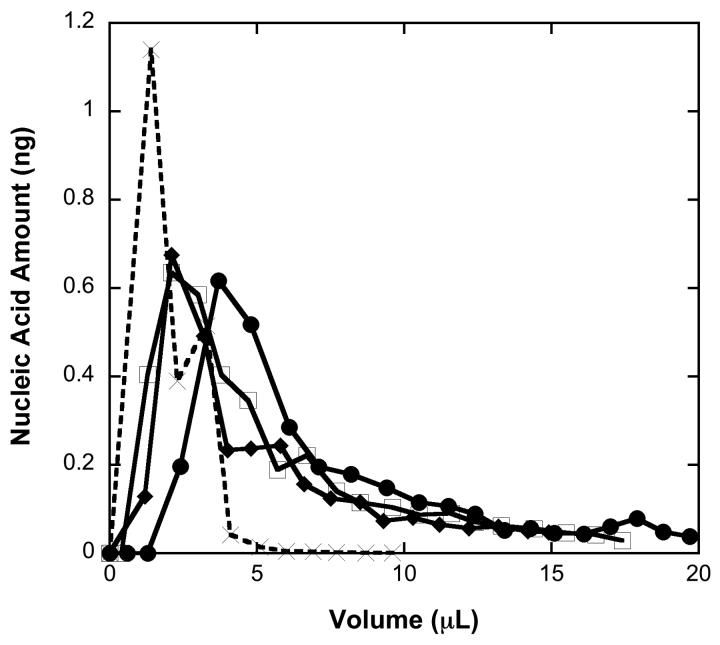
Figure 5 shows the DNA elution profiles of three nominally identical μSPE columns described previously and the RNA elution profile for influenza A virus. The DNA elutes in a highly reproducible manner, with less than 10 percent variability in the amount of DNA recovered. Approximately 50 percent of the eluted DNA is contained in the first 3 μL of water emerging from the column. Thus, the μSPE device appears to be able to efficiently concentrate DNA with an overall DNA recovery of ca. 30 percent.

Fig. 5.

DNA elution profiles (solid line) of the μSPE device at a flow rate of 100 μL h⁻¹ with 6 M GuSCN (pH 8.0) solution and DNA loading concentration of 1 ng μL⁻¹. The data are for three replicates. RNA elution profile (dashed line) of the μSPE device for influenza RNA at a flow rate of 100 μL h⁻¹ with 6 M GuSCN (pH 8.0) solution and NA loading concentration of 1 ng μL⁻¹.

The elution behavior and recovery efficiency of RNA is also of interest as discussed previously. Figure 5 shows elution profiles for influenza RNA and λ-DNA under identical process conditions. Based on this single run, the RNA elutes in a higher initial spike, but overall recovery of the RNA was ca. 20 percent.

Case study to determine relative amounts of target to total NA in MDCK cells infected with influenza A virus

Design of a miniature purification unit will require an estimate of the ratio of target to total NA in the specimen of interest. To generate this estimate for the influenza system studied here, an infectious biological sample consisting of cultured MDCK cells infected with influenza A virus was prepared to determine the ratio of target NA to total NA present in a sample resembling what would be obtained from an infected patient.

By purifying ∼10⁶ infected cells with a QIAamp kit, it was determined with UV spectrophotometry that 1.3 μg of total NA was present, corresponding to a concentration of ca. 1.3×10⁻³ ng NA per cell. A similar experiment was performed where again ∼10⁶ infected cells were purified, but this time with an RNeasy kit, which purifies RNA. It was determined by real-time reverse transcription PCR that ca. 0.0735 ng of the HA1 target gene (987 base pair single-stranded RNA, ca. 320 kDa) was present, which corresponds to ca. 68 million copies of this gene. From the molecular weight of the HA1 domain, the mass fraction of target viral RNA to total NA in the sample is 6×10⁻⁵. This mass fraction allows us to determine the number of copies of target gene present in a sample if the number of infected cells or the mass of total NA is known, which allows us to estimate how much starting material we need for a successful detection based on the sensitivity of our assay, as discussed in the section that follows.

Design procedure based on the Ergun equation

The results of the experiments discussed in this paper provide the basis for designing a silica-based solid-phase-extraction NA purification device. Discussed here is a step-by-step procedure to determine design variables such as channel dimensions, liquid volumes, liquid flow rates and the mass of silica required based on the characterization reported in previous figures, with sample calculations given for a case study based on the biological parameters obtained from the infected MDCK cellular material.

The primary equation that will be used for design purposes is the Ergun equation [13], relating the volumetric flow rate through the packed bed to the pressure drop across it. While the Ergun equation was derived by crudely modeling the packed bed as a bundle of straight tubes with a total internal surface area equal to that of the packed particles, the form of the relationship between pressure drop, packing length and flow rate can be established by simple dimensional analysis and is valid in both the laminar and turbulent regimes as long as channeling and fluidization of the bed are absent. The coefficients of the equation, and the dependence on void fraction will depend on the particular geometry of the particles (i.e., their shape and size distributions). The Ergun equation is given by:

$$\frac{\Delta {\mathit{PD}}_P}{L}\left(\frac{{\Phi }^3}{1-\Phi }\right)=\frac{150\mu (1-\Phi )Q}{D_{P}A}+\frac{1.75\rho Q^2}{A^2}$$ (1)

where ΔP is the pressure drop across the silica channel, D_P is the mean silica particle diameter assuming heterogeneous spherical particles,Φ is the porosity of the silica channel, L is the length of the silica channel, μ is the fluid viscosity which is taken to be a constant, ρ is the fluid density, Q is the volumetric flow rate and A is the cross-sectional area of the silica channel. The Ergun equation is valid for heterogeneous spherical particles.

Assuming laminar flow and neglecting the inertial term (a very good approximation for the slow flow rates we consider), the Ergun equation reduces to the Carmen-Kozeny equation, which is:

$$\frac{\Delta {\mathit{PD}}_P}{L}\left(\frac{{\Phi }^3}{1-\Phi }\right)=\frac{150\mu (1-\Phi )Q}{D_{P}A}$$ (2)

For our case study, D_P is assumed to be 5 μm based on particle size distribution (0.1-10 μm), Φ is 0.3 and μ is 0.1 g cm⁻¹s⁻¹. If the viscosity of the solution proves to be different than that of water, as could likely be the case for clinical specimens, this situation is straightforward to accommodate in Equation 2 because the solution viscosity, μ, appears explicitly. Operating at the maximum possible pressure drop in Equation 2 would yield the maximum flow rate possible for the process, allowing the shortest purification time. Operating at this value we have:

$$\Delta \mathrm{P}=350\mathrm{kPa}$$ (3)

which is valid for a bonded PDMS-glass device [15]. For other kinds of devices, a different maximum operating pressure would hold.

The unknowns in Equation 2 are A, L and Q, which specify channel dimensions and the maximum flow rate through the channel. Based on the Ergun equation alone, the problem is underspecified with two degrees of freedom. To obtain feasible values for these unknowns, additional equations are necessary. These equations will come directly from constraints we will set on the unknown variables, which will specify the design problem.

For simplicity, we will only consider square cross-sectional areas:

$$A=W^2$$ (4)

where W is the width of the silica channel. The unknown variables pertaining to channel dimension are L and W, and two constraints need to be set on these variables. The first constraint ensures the channel width is significantly greater than the diameter of a single silica particle:

$$W=10D_P$$ (5)

where D_P is the mean particle diameter, which is 5 μm for our case study, with the largest silica particles being 10 μm in diameter. If the ratio between the largest particle diameter and mean diameter is greater than two, Equation 5 would need to be adjusted accordingly. The factor of 10 allows efficient packing, prevents fluidization of the packed bed and can be adjusted based on experiment. For our case study, based on the range of particle sizes, the channel width must be at least 50 μm. The second constraint relates L and W. From chromatography, a key design constraint for any solid-phase separation device is the aspect ratio, which is the ratio of the length to the width of the separation channel. To minimize channeling and ensure low dispersion characteristics, a channel with a reasonably high aspect ratio is required. We therefore specify the aspect ratio as:

$$\frac{L}{W}\ge 5$$ (6)

The factor of five will be used for illustration but can be considered a parameter to be tailored based on the desired device geometry. A packed channel with low dispersion characteristics would elute bound NA in a sharp spike, as illustrated in Figure 5, allowing the purified NA to be recovered in a minute liquid volume to help ensure compatibility with a downstream PCR detection device.

Based on the Ergun equation, the maximum volumetric flow rate Q is set by the maximum pressure drop the device can withstand. Q also needs to be sufficient to be compatible with a portable device used for “rapid” genotyping. Possible values of Q depend on t_Purification, the maximum time specified for the entire purification process to be completed:

$$t_{\mathit{Purification}}\le 30\min$$ (7)

A constraint of 30 min was used for t_Purification based on reasonable expectations for portable PCR detection. For example, a device requiring about 20 min for complete detection has been reported in the literature [16]. The constraint on purification time defines the constraint on the volumetric flow rate through the device:

$$Q\ge \frac{V_{\mathit{Load}}+V_{\mathit{Wash}}+V_{\mathit{Elute}}}{t_{\mathit{Purification}}}$$ (8)

where V_Load is the volume of NA-containing chaotropic salt loading buffer, V_Wash is the volume of washing buffer and V_Elute is the volume of water used to elute the NA. For the case study, we will assume that the washing and elution steps utilize a similar volume of liquid as the loading step; thus we can take the volumetric flow rate to be Q ≥ 3V_Load / t_Purification. If V_Load is much larger than the pore volume of the bed, then the washing and elution volumes might be made much less than V_Load. In that case, the minimum volumetric flow rate, or alternatively the purification time could be reduced, but by no more than a factor of three. Explicit determination of V_Load depends on the pathogen and sample type chosen for detection in an assay and can be determined from our case study data on the infected MDCK cells. We find that Q ≥ 15 μL h⁻¹.

With the constraints on channel dimension and flow rate specified, the design problem based on the Ergun equation can be solved. With no other fundamental equations relating channel dimension or flow rate, a constraint equation needs to be inserted into Equation 2, the laminar-flow version of the Ergun equation, as an equality to obtain a set of possible solutions. From the constraints on channel width, aspect ratio and volumetric flow rate, we will fix the aspect ratio from Equation 6 for illustration:

$$\mathrm{L}=5\mathrm{W}$$ (9)

Inserting Equation 9 into the Equation 2 leaves two unknown variables, Q and W. The equation can be solved explicitly:

$$Q=\frac{\Delta {{\mathit{PD}}_P}^2}{750\mu }\frac{{\Phi }^3}{{(1-\Phi )}^2}W$$ (10)

allowing maximum flow rates to be determined based on channel width. Figure 6 illustrates the linear relationship between flow rate and channel width, and specifies all design constraints. Based on Figure 6, a silica channel with a width of 65 μm and a length of 325 μm could function at a flow rate of 15 μL h⁻¹, meeting all design constraints set forth and setting a lower bound on the design. The volume of loading buffer necessary, determined in the next section, sets the upper bound on the design. V_Load should not be less than the pore volume of the packed bed to insure adequate interaction between the chaotropic salt buffer and the silica particles. For our case study, the upper bound is specified by a channel width of 0.53 mm and a length of 2.66 mm, which is large enough that its pore volume could hold the entire injected sample. To process the load, wash, and elution steps through this larger bed, a flow rate of ca. 127 μL h⁻¹ is required. Note that despite this higher flow rate and longer channel, the pressure drop is the same as for the smaller bed, since the width of the square channel is also larger, and therefore the average velocity through the bed is actually lower for the larger bed.

Fig. 6.

Plot of Q versus W from the Ergun equation, assuming an aspect ratio of 5. (1) indicates Q and W for a channel incorporating the minimum mass of silica. (2) indicates Q for a channel that meets the constraint of channel width. (3) indicates W for a channel that meets the constraint on flow rate. The dotted red line indicates solutions that do no meet any design constraints. The dashed blue line indicates solutions that do not meet the constraints W ≥ 50 μm and Q ≥ 15 μL h⁻¹. The dotted-dashed green line indicates solutions that do not meet the constraint Q ≥ 15 μL h⁻¹. The solid black line indicates possible design solutions that meet all constraints, and has an upper bound set by the sample volume.

Since the design presented in Figure 6 only offers solutions for an aspect ratio of 5, design specifications for higher aspect ratios could be determined by varying the constraint in Equation 6. It should be noted that design specifications for devices constructed of materials such as PDMS, which cannot withstand large pressure drops, typically have a limited range of aspect ratios capable of providing solutions that meet the constraint on flow rate and provide micron-scale channel dimensions.

From the channel dimensions obtained in Figure 6, the amount of silica needed for a particular channel volume can be determined by:

$$\alpha ={\mathit{LW}}^2(1-\Phi ){\rho }_{\mathit{Si}}$$ (11)

where α is the mass of silica, Φ is the porosity of the silica channel and ρ_Si is the density of silica. For our case study, L is 325 μm, W is 65 μm, Φ is 0.3 and ρ_Si 1.8 g cm⁻³. From these values the mass of silica is ca. 1.7 μg.

Based on the design procedure thus far, the silica mass determined by Equation 11 is based solely on the channel dimensions obtained from the Ergun equation. To determine whether this mass of silica calculated is sufficient for the assay of interest, the minimum mass of silica needed to purify a specific sample needs to be determined. The minimum mass of silica, α_min, is:

$${\alpha }_{\min }=\frac{M_{\mathit{Total}}}{\Gamma S}$$ (12)

where M_Total is the mass of NA required in the loading buffer, Γ is the mass of NA that can be adsorbed to the silica surface per unit area of silica as determined by the adsorption isotherms in Figures 2 and 3 (assuming negligible adsorption of other molecules), and S is the effective surface area per unit mass of the silica particles. M_Total incorporates several experimental parameters and is discussed in detail in the appendix. For the case study based on the MDCK cells infected with influenza A virus discussed in the previous section, we assume that 10,000 copies of the target NA sequence are needed from the purification unit, that there is 9.9×10⁻⁹ μg NA per target NA copy in the sample, and that the column extracts NA with an efficiency of 30 percent, we find that M_Total is 3.3×10⁻⁴ μg NA, Γ is 1850 μg NA per m² silica and S is 6.9 m² silica per g silica. Based on these values the minimum mass of silica needed to purify a sample is ca. 0.026 μg. Γ is based on the amount of NA that can be adsorbed to a specific surface area of silica and is thus independent of the silica size used. This quantity can be simply determined from the adsorption isotherm results of Fig 2-4 for a wide range of purification designs including those involving silica of varying size. S can vary depending on the type of silica particles used for purification and can be adjusted in Equation 12 to accommodate particles of any size distribution.

Since, in our case, α_min < α, our original design is complete and we can use the calculated design specifications as a starting point for building an optimized micro NA purification device. However, if α_min > α, a larger channel width would be required in order to have enough silica surface area to adsorb all the NA needed for the assay. The possibility of an unusable solution exists if the channel dimensions needed to incorporate a sufficient amount of silica exceed the upper bound set by the volume of loading buffer.

The procedure presented thus far can also be generally applied to determine design solutions for cases in which we wish to vary other parameters in the Ergun equation such as the particle diameter D_P. To determine if D_P can be varied to provide feasible designs, the effective surface area of silica per unit mass, S, needs to be defined as a function of the effective particle diameter, D_P^eff:

$$S=\frac{6}{{\rho }_{\mathit{Si}}{D}_P^{\mathit{eff}}}$$ (13)

For our case study, D_P^eff is 0.48 μm for a mean particle diameter of 5 μm. This difference between the “mean” and “effective” particle diameter simply reflects the fact that a disproportionate share of the surface area is in the smaller-sized particles. It is assumed that the effective particle diameter and mean particle diameter are directly proportional; this means that the particle size distribution is assumed to be the same shape when the mean particle size is changed. Inserting S from Equation 13 into Equation 12 allows us to calculate α_min for specific values of D_P^eff.

From the Ergun equation, there are now four unknowns: D_P, L, Q and W. The problem is underspecified with three degrees of freedom. To obtain a feasible design, two constraint equations need to be incorporated into the Ergun equation. As before, setting the aspect ratio to five eliminates the unknown L from the Equation 2. Additionally, the constraint in Equation 5 can be fixed:

$$W=10D_P$$ (14)

which eliminates the unknown W from the Ergun equation. The relationship between the two unknown variables, D_P and Q, can now be determined explicitly:

$$Q=\frac{\Delta P{\Phi }^3}{75\mu {(1-\Phi )}^2}{D_P}^3$$ (15)

The relationship between mean particle diameter and maximum flow rate is illustrated in Figure 7, providing possible design solutions for the case study. Based on Figure 7, for our particular case study, a mean particle diameter of 5.5 μm, a channel width of 55 μm, a channel length of 275 μm and a silica mass of ca. 1 μg (α_min = 0.026 μg) could function at a flow rate of 15 μL h⁻¹, thus meeting all design constraints.

Fig. 7.

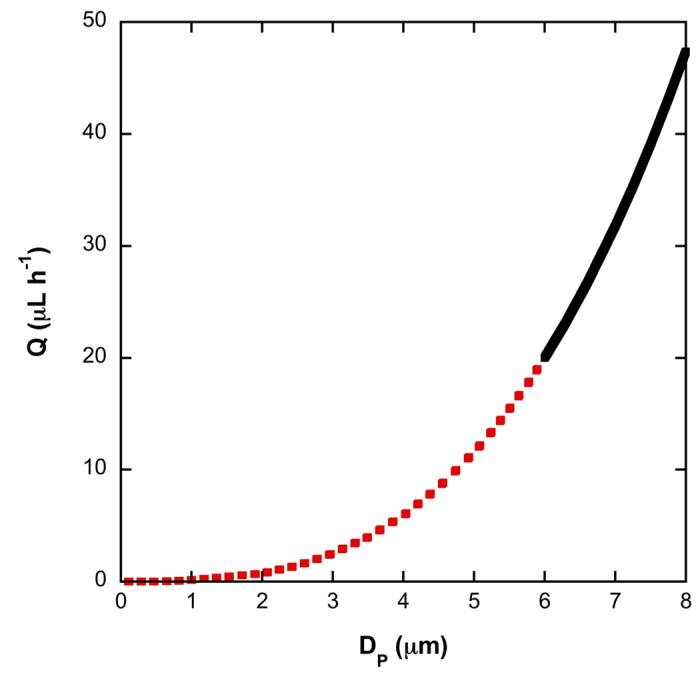
Plot of Q versus D_P from the Ergun equation assuming an aspect ratio of 5 and W = 10D_P. The dotted red line indicates solutions that do not meet the constraint Q ≥ 15 μL h⁻¹ and the solid black line indicates possible design solutions that meet all constraints and has an upper bound set by the amount of sample volume.

Note that for the design based on 5 μm particles, the channel needed to be 65 μm wide (and equally deep) and 325 μm long, giving it a channel volume and mass of silica that is larger than that for the 5.5 μm particles by a factor of 1.7. The larger channel size for the 5 μm particles was dictated by the need to achieve purification in 30 minutes or less; the smaller 5 μm particles generate too large a pressure drop for the volumetric flow rate needed to achieve the set separation time unless the channel is at least 65 μm wide. By increasing the particle size to 5.5 μm, the average linear velocity through the channel is faster for a given pressure drop, so that the needed volumetric flow rate can be achieved even if the channel is narrowed to the minimum (W = 55 μm) needed to maintain the ratio W/D_P at 10. The channel length also then can be decreased, while still retaining the needed minimum aspect ratio L/W = 5. Thus, a modest increase in particle diameter, from 5 to 5.5 μm, decreases the bed volume, and mass of silica, by a factor of 0.6.

We could increase the particle size still more; however, the channel width and length would need to be increased in proportion to the particle diameter to maintain the ratios W/D_P = 10 and L/W = 5; hence the mass of silica needed would increase as the cube of the particle diameter. The separation could be achieved in the same amount of time, since Equation 15 shows that the volumetric flow rate can be increased as the cube of the particle diameter, for a fixed pressure drop, when W/D_P = 10 and L/W = 5. However, there would be no point to doing this, as it would simply increase the channel volume with no reduction in the separation time.

One might wonder why there would not be an advantage to using much smaller particles, which would have a much larger surface area per unit volume, and thus allow a smaller channel to be used. The answer is that the linear flow rate through such a tight porous medium would need to be much lower to prevent over-pressuring the bed. And since the volume of fluid that must be pushed through the bed is set by the sample volume, not by the pore volume of the bed, the slower velocity cannot be compensated by any reduction in fluid volume that must be forced through the bed. Thus, in essence, the ideal particle size is controlled by the fluid volume of the sample that must be pushed through the bed. If this volume can be reduced, say, by a factor of 10, either by a reduction in the amount of DNA that needs to be recovered, or by pre-concentrating the sample, for example by evaporation of water, then the same separation time (30 min) is achievable with one-tenth the volumetric flow rate (1.5 μL h⁻¹), and according to Equation 15, the particle size could then be decreased by the cube root of this, and the bed volume would also decrease by ca. 10-fold, making for a more compact channel. Alternatively, the particle size and channel dimensions could be left the same, and a separation in 3 min, rather than 30 min, could be achieved.

Another way to further optimize the design might be to narrow the distribution of particle diameters. For the design procedure thus far, we have considered heterogeneous spherical particles, for which the effective particle diameter D_P^eff controlling the particle surface area is an order of magnitude smaller than the mean particle diameter D_P. If the particles are homogeneous in size, we no longer need worry about unusually large particles in the tail of the distribution that must be accommodated by a correspondingly large channel width. The relationship between particle diameter and flow rate for homogeneous spherical particles can be determined by relaxing the constraint on the minimum ratio of channel width to particle diameter:

$$W=5D_P$$ (16)

where D_P is now the homogeneous particle diameter. Since for the heterogeneous particles, the channel width was chosen in Equation 14 to be 10 times D_P, which was 5 times the size of the largest of the heterogeneous particles, Equation 16 for homogeneous particles is really identical to Equation 14 for the heterogeneous particles used in the case study. Incorporating Equations 9 and 16 into the laminar version of the Ergun equation:

$$Q=\frac{\Delta P{\Phi }^3}{150\mu {(1-\Phi )}^2}{D_P}^3$$ (17)

Based on Equation 17, a particle diameter of 10.5 μm, a channel width of 52.5 μm and a channel length of 262.5 μm could function at a flow rate of 15 μL h⁻¹. The silica mass of 0.9 μg needed for this channel meets the requirement of 0.6 μg of silica.

In these designs, the channel contains much more silica surface area than needed to capture the NA required for the detection assay. Faster purifications of the same amount of NA could be achieved, however, by pre-concentrating the solution to be purified to reduce the volume that needs to be pushed through the bed. Some of the above findings (i.e. larger particles, with smaller total surface area per unit mass allows a smaller purification channel to be used) are counterintuitive, and illustrates the need for careful consideration of factors governing the purification, if optimally compact and rapid purification is to be achieved.

Conclusions

We have evaluated adsorption and elution behavior of NAs to the surface of silica in the presence of a chaotropic salt buffer, and have described a method to design a micro-purification column utilizing colloidal silica. Our method allows estimation of the channel dimensions, fluid flow rate, sample volume and amount of silica needed for a particular pathogen and sample type. The design procedure is based on a pressure-flow equation for a packed bed of particles. The design is influenced by two primary constraints; the maximum pressure drop possible on a device and the time required for purification. These constraints can be met by adjusting parameters such as the size of the particles used, the amount of NA in a given sample and the operating flow rate of the purification procedure. Detailed description of this design method is presented.