Second virial coefficients as a measure of protein–osmolyte interactions

Abstract

The cytoplasm contains high concentrations of cosolutes. These cosolutes include macromolecules and small organic molecules called osmolytes. However, most biophysical studies of proteins are conducted in dilute solutions. Two broad classes of models have been used to describe the interaction between osmolytes and proteins. One class focuses on excluded volume effects, while the other focuses on binding between the protein and the osmolyte. To better understand protein–smolyte interactions, we have conducted sedimentation equilibrium analytical ultracentrifugation experiments using ferricytochrome c as a model protein. From these experiments, we determined the second virial coefficients for a series of osmolytes. We have interpreted the second virial coefficient as a measure of both excluded volume and protein–osmolyte binding. We conclude that simple models are not sufficient to understand the interactions between osmolytes and proteins.

The cellular medium in which proteins must function contains high concentrations of cosolutes. The cosolutes include proteins, nucleic acids, and osmolytes, low molecular weight organic molecules with no net charge. Some organisms change their osmolyte composition in response to environmental stresses. For example, cartilaginous marine fish use trimethylamine N-oxide (TMAO) to counteract high concentrations of urea (Yancey et al. 1982). Here, we present data on the interaction between iso-1-ferricytochrome c and osmolytes.

Contrary to cellular conditions, most biophysical studies are conducted in dilute solutions (i.e., in the absence of cosolutes). Therefore, data from these studies may bear little resemblance to the way proteins behave in vivo (Zimmerman and Minton 1993).

Many osmolytes stabilize proteins in vivo and in vitro (Hofmeister 1888; Singer and Lindquist 1998; Saunders et al. 2000). However, the stabilization mechanism is poorly understood. In general, two classes of models are used to explain the effects of osmolytes on protein stability (Saunders et al. 2000 and references therein). The first class focuses on the binding between osmolytes and proteins. The other class focuses on excluded volume effects arising from the increased steric repulsions between osmolytes and the protein. The binding models claim that osmolyte-induced stability increases arise from preferential binding of the osmolyte to the native state. The excluded volume models focus on the fact that osmolytes limit the conformational freedom of proteins by driving them to their most compact state, the native state. The decrease in conformational freedom arises from steric repulsions between the protein and the osmolyte.

The actual mechanism must be a combination of the two classes, and models based on this combination lead to valuable insight. The fact that osmolytes take up space in solution cannot be denied. The resulting steric repulsion is shown by osmolyte-induced stabilization of the A-state of cytochrome c in the absence of counterions (Davis-Searles et al. 1998; Saunders et al. 2000). The intramolecular repulsions from the positively charged residues in the A-state should overwhelm any stability gained from osmolyte binding. In this instance, steric repulsion between the osmolytes and the acid-denatured state drives the protein into the A-state. Osmolytes have also been shown to preferentially interact with the native state, for example, trehalose with aldolase (Xie and Timasheff 1997). The questions that need to be posed are, To what extent do different osmolytes interact with proteins both through steric repulsions and through binding equilibria? and Do these interactions vary between proteins? Both questions are addressed here.

We examined the interaction of osmolytes with the model protein ferricytochrome c by using sedimentation equilibrium analytical ultracentrifugation (SE). We determined the second virial coefficient (B_A,M), the change in cytochrome c activity with respect to osmolyte concentration, for a series of osmolytes. At low-protein concentrations, B_A,M can be determined by measuring the apparent buoyant molecular weight of cytochrome c (M_A,buoy) as a function of osmolyte concentration (C_M). Neglecting higher order terms, B_A,M is determined by using the following equation (Jacobsen et al. 1996):

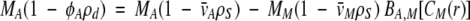1

Here the subscripts A and M denote cytochrome c and the osmolyte, respectively. M_X is the molecular weight, φ_A′ is the apparent partial specific volume, ρ_d is the density of the solution, ρ_S is the density of pure solvent, v¯ is the partial specific volume (0.73, 0.61, 0.84, and 0.96 cm³ g⁻¹ for cytochrome c, polyols, betaine, and TMAO, respectively [Durchschlag 1986]), and C_M(r) is C_M as a function of radial distance in the ultracentrifuge cell. For small cosolutes such as the ones studied here, C_M(r) is constant because the rotor speed required to form a protein concentration gradient is too low to form an osmolyte concentration gradient. In equation 1, the left-hand side is M_A,buoy in the cosolute solution, the first term on the right-hand side is M_A,buoy in dilute solution, and the second term on the right contains the buoyant molecular weight of the osmolyte (M_M,buoy). Linear regression of M_A,buoy with respect to C_M yields a slope that depends on B_A,M and M_M,buoy. We have assumed that v¯ does not change when osmolytes are added to the solution. This assumption has certainly been shown to be correct for aldolase (Ebel et al. 2000).

Virial coefficients are fundamental thermodynamic parameters. In the present situation, B_A,M is the coefficient of the term in C_AC_M and, hence, includes a contribution from complex formation between A and M, as well as the contribution from physical (i.e., excluded volume) protein–cosolute interactions. According to the model used here, B_A,M = B*_A,M − K_A,M, where B*_A,M and K_A,M are the notional coefficients for the nonassociative and associative clusters, respectively (Wills et al. 2000). Interpreting the experimentally measured thermodynamic parameter B_A,M, thus, becomes model dependent because any conclusion about the magnitude of the solute–cosolute binding constant depends on the value assigned to the coefficient for nonassociative clustering. Only in instances in which B_A,M is negative (see data below for stachyose) can cosolute binding be established unequivocally, for B*_A,M is necessarily positive. Nevertheless, the assignment of a reasonable estimate to the covolume radius r_A,M (=r_A + r_M [Schachman and Lauffer 1949]) allows the calculation of B*_A,M and, hence, a consequential inference about the magnitude of K_A,M.

Interpreting fundamental thermodynamic parameters at the molecular level requires a model. Although models distort a parameter's meaning, models are useful if they provide physical insight. The model used here interprets B_A,M as a measure of the extent of steric repulsion and protein–osmolyte binding. If the interaction between the osmolyte and the protein is limited to steric repulsions, B_A,M will equal B*_A,M (Jacobsen et al. 1996). Assuming that both species are spheres, the covolume radius (r_A,M) calculated from B_A,M should equal the sum of the protein and osmolyte radii (r_A + r_M). If the osmolyte binds to the protein, then r_A,M will be smaller than the sum. If repulsive charge–charge interactions (i.e., Donnan effects) between the protein and the osmolytes are important, then r_A,M will be larger than the sum.

Results

Osmolytes interact with cytochrome c

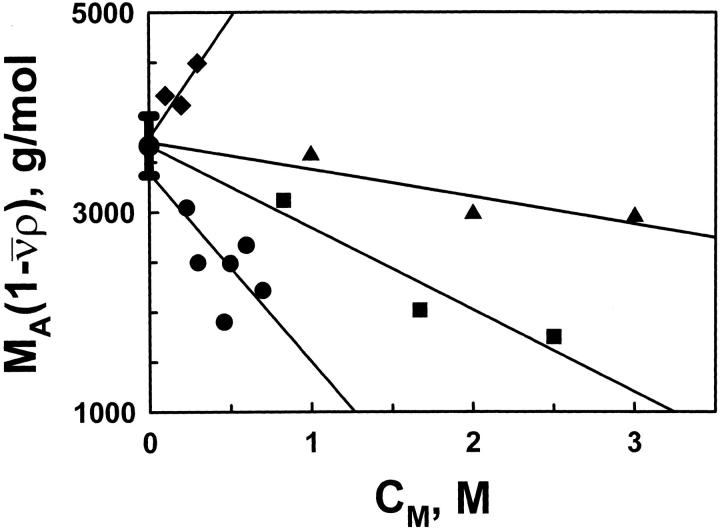
The buoyant molecular weight decreases linearly with osmolyte concentration for each osmolyte except stachyose (Fig. 1 ▶). Fitting to a linear model allows the calculation of B_A,M and, subsequently, r_A,M (Table 1). M_A,buoy in dilute solution is 3700 ± 300 g/mole, which corresponds to a molecular mass of 13.7 kD ± 1.1 kD. This molecular mass is within error of that calculated from the sequence, 12.7 kD.

Fig. 1.

Plots of the buoyant molecular weight of cytochrome c M_A(1–v¯ρ) versus molar osmolyte concentration C_M for betaine (triangle) glucose (square), melezitose (circle) and stachyose (diamond). The uncertainty (±300 g/mole⁻¹) for no osmolyte is from five repetitions and is assumed to be representative of all uncertainties. The lines are linear least-squares fits. The slopes −dM_A,buoy/dC_M are shown in Table 1.

Table 1.

Protein-osmolyte excluded volumes

Osmolyte	MM (g mole−1)	rM,calca (Å)	−dMA,bouy/dCMb (g L mole−2)	BA,Mc,e (L mole−1)	rA,Md,e (Å)
TMAO	111	2.7	140 ± 100	32 ± 24	38 ± 10
betaine	135	3.1	270 ± 80	13 ± 4	17 ± 2
glucose	180	3.2	800 ± 100	12 ± 2	17 ± 1
sucrose	342	4.0	1400 ± 500	10 ± 4	16 ± 2
melezitose	504	4.6	1900 ± 700	10 ± 3	16 ± 2
stachyose	667	5.0	−2400 ± 800	−9 ± 3	naf

^a Osmolytes radii (r_M,calc) were calculated by using the method of Edward (1970).

^b The uncertainties for −dM_A,bouy/dC_M are the standard deviations for a linear regression of the buoyant molecular weight of cytochrome c on osmolyte concentration.

^cB_A,M was calculated from −dM_A,bouy/dC_M by using equation 1.

^dr_A,M was calculated from B_A,M by using the equation 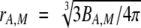and applying the assumptions discussed in the text.

^e The uncertainties for B_A,M and r_A,M are from propagating the uncertainties (Taylor 1982) in −dM_A,bouy/dC_M through equation 1 and then through the equation in footnote d.

^f Not applicable.

To test our model, it is helpful to define a range of r_A,M values that can be compared to the observed value. If the observed value is within this range, then the interaction between the protein and the osmolyte is limited to steric repulsions. If the observed value is larger than this range, then there are Donnan effects. If the observed value is smaller than this range, then the osmolyte binds to the protein. The sum of the hydrated radii define the upper limit for r_A,M, and the sum of the unhydrated radii define the lower limit (Winzor and Wills 1995).

The unhydrated osmolyte radii were calculated by using a bond-counting procedure (Edward 1970). These radii range between 2.7 Å for TMAO and 5.0 Å for stachyose (Table 1). The hydrated radii of glucose and sucrose, the only two osmolytes that have reported hydrated radii, are 2.5 and 3.2 Å, respectively (Winzor and Wills 1995). The unhydrated radius of cytochrome c, 16 Å, was calculated by using the equation 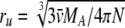, where N is Avogadro's number (Winzor and Wills 1995). The hydrated radius of cytochrome c, calculated from solvent accessible surface area, is 22 Å (Saunders et al. 2000). Therefore, if steric repulsion is a complete explanation for the interaction of cytochrome c with the osmolytes, then r_A,M values calculated from B_A,M should be 20–27 Å (Table 1).

With the exception of TMAO, the observed values of r_A,M derived from B_A,M are less than the smallest calculated r_A,M values. This supports the idea that the polyols and betaine bind to cytochrome c. These data also suggest that only TMAO is completely excluded from the surface of cytochrome c.

Discussion

Stachyose causes aggregation

Aggregation is shown by the direct dependence of the M_A,buoy on stachyose concentration (Fig. 1 ▶), but the cause of this aggregation remains unclear. Stachyose differs from the other polyols studied in that it is larger and contains two galactose moieties. Sucrose and melezitose have only glucose and fructose moieties. However, thermal denaturations of cytochrome c in the presence of galactose and glucose yield similar results (Saunders et al. 2000), which is inconsistent with the galactose moieties causing the aggregation.

Osmolytes interact differently with cytochrome c and bovine serum albumin

Comparing our data for cytochrome c to vapor pressure osmometry data for bovine serum albumin (Courtenay et al. 2000) show that osmolytes interact differently with these two model proteins. Both studies show that polyols bind to proteins. Betaine is most excluded from bovine serum albumin and TMAO is only slightly more excluded than the polyols, whereas TMAO is completely excluded from cytochrome c, while betaine behaves like a polyol. The constant radius observed for the polyols, despite the size range, may reflect compensation between binding and osmolyte size.

Both betaine and TMAO are zwitterions, whereas the polyols are uncharged. Interactions between the charged groups of zwitterions and proteins may depend on the surface potential of the protein. In addition, we may be observing Donnan effects between cytochrome c and TMAO that further repel this osmolyte from the protein surface.

Conclusions

Proteins have evolved to function within a solution crowded with other proteins, nucleic acids, and osmolytes. However, most experiments are conducted in dilute solutions and little is known about the interactions between proteins and osmolytes. There are two simple theories for these interactions (Saunders et al. 2000). One theory states that osmolytes interact with proteins solely through steric repulsions, and the second contends that there are binding equilibria between proteins and osmolytes. The experiments described here offer a systematic approach for dissecting these interactions.

Our data show that with the exception of TMAO, all the osmolytes studied bind cytochrome c. This conclusion is in general agreement with the results from the bovine serum albumin study (Courtenay et al. 2000). However, betaine is most excluded from bovine serum albumin, whereas TMAO is most excluded from cytochrome c. These two sets of experiments show that steric repulsions alone are not enough to describe the interaction between osmolytes and proteins. These data also show that osmolytes interact differently with each protein. In conclusion, it appears that simple models are not sufficient to understand osmolyte–protein interactions.

Materials and methods

Protein purification

The C102T variant of Saccharomyces cerevisiae iso-1-ferricytochrome c was used throughout. This variant facilitates biophysical characterization but does not alter the structure or function of the protein (Cutler et al. 1987; Gao et al. 1991; Berghuis and Brayer 1992). Recombinant cytochrome c was purified from Escherichia coli, as described previously (Pollock et al. 1998; Morar et al. 1999). After purification, cytochrome c was oxidized with NH₄(Co[dipicolinate]₂; Mauk et al. 1979). The protein was then dialyzed into 50 mM dimethyl glutarate (DMG), pH 6.0, and concentrated to ∼0.7 mM. The concentrated protein was stored at 4°C. Distilled and deionized water was used throughout.

Sample preparation

d(+)-glucose, sucrose (>99.5%), d(+)-melezitose (minimum 99%), stachyose (minimum 98%), TMAO (dihydrate), and betaine (anhydrous) were purchased from Sigma and used without further purification. Cytochrome c was exchanged into the highest concentration of each osmolyte by diluting the protein into a solution containing 50 mM dimethyl glutamate buffer (pH 6.0) plus the osmolyte, concentrating the protein with a Centricon concentrator (10,000 molecular weight cutoff; Millipore), and then diluting again with a high-concentration osmolyte solution. The sample was then diluted to the appropriate osmolyte concentration with 50 mM buffer (pH 6.0). The final protein concentration was ∼5 μM.

Analytical ultracentrifugation

Sedimentation equilibrium experiments were performed with a Beckman XLA ultracentrifuge at the Macromolecular Interactions Facility at the University of North Carolina at Chapel Hill. The six-chamber cells were used as follows: Three chambers contained cytochrome c and three chambers contained buffer. The system was considered to be at equilibrium when the last two scans overlaid. The experiments were conducted at 20°C at a rotor speed of 20,000 rpm. Absorbance-versus-radial position traces were recorded at 410 nm.

Data analysis

Using Winnonlin version 1.035 for Win95 and WinNT, the data were fit to the following equation

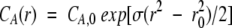2

where r is the radial position, r₀ is the radius at the meniscus, C_A(r) is the concentration of protein as a function of r, C_A,0 is the concentration at r₀,and

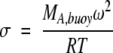where ω is the angular velocity of the rotor, R is the gas constant in ergs mole⁻¹ K^-1, and T is the absolute temperature (Johnson et al. 1981; Laue 1995; ftp://spin6.mcb.uconn.edu/pc/win95/winnonln/). The residuals showed no systematic pattern. M_A,buoy was determined from σ. Plots of M_A,buoy versus C_M were fit to equation 1 to determine B_A,M (Fig. 1 ▶). The results are independent of rotor speed (data not shown).