Abstract
Maize (Zea mays ssp. mays) is genetically diverse, yet it is also morphologically distinct from its wild relatives. These two observations are somewhat contradictory: the first observation is consistent with a large historical population size for maize, but the latter observation is consistent with strong, diversity-limiting selection during maize domestication. In this study, we sampled sequence diversity, coupled with simulations of the coalescent process, to study the dynamics of a population bottleneck during the domestication of maize. To do this, we determined the DNA sequence of a 1,400-bp region of the Adh1 locus from 19 individuals representing maize, its presumed progenitor (Z. mays ssp. parviglumis), and a more distant relative (Zea luxurians). The sequence data were used to guide coalescent simulations of population bottlenecks associated with domestication. Our study confirms high genetic diversity in maize—maize contains 75% of the variation found in its progenitor and is more diverse than its wild relative, Z. luxurians—but it also suggests that sequence diversity in maize can be explained by a bottleneck of short duration and very small size. For example, the breadth of genetic diversity in maize is consistent with a founding population of only 20 individuals when the domestication event is 10 generations in length.
Keywords: Adh1, Zea, coalescent
The process of crop domestication is a mystery, but this much is known: most crops contain less genetic variation than their wild ancestors. This reduction in genetic variation is probably a product of a small initial crop population, coupled with intense selection for agronomic traits (1). In short, the initial steps of most domestication events probably included a population bottleneck (hereafter called a “domestication bottleneck”). The effects of these bottlenecks are important, both because they limited genetic variation in crops and because the dearth of genetic variation in modern crop varieties is a growing concern (1). To counter this concern, there have been increased efforts to incorporate exotic germplasm into crop breeding programs (2, 3). These breeding efforts will be aided by a better understanding of both the domestication process and the dynamics of domestication bottlenecks.
In this study, we explore the domestication bottleneck of maize (Zea mays ssp. mays). The domestication of maize is intriguing for two reasons. First, maize is morphologically distinct from its wild relatives. The wild progenitor of maize was identified unambiguously as an annual member of the genus Zea only through the application of molecular markers (4, 5). Second, maize is genetically diverse. For example, maize appears to contain greater isozyme diversity than many wild plants (4), and other genetic measures, including chromosomal knobs (6), chloroplast restriction fragment length polymorphism data (5), nuclear internal transcribed spacer sequences (7), and nuclear single-copy sequences (8–10), also indicate that maize is genetically diverse. These two features of maize are somewhat contradictory. On the one hand, high genetic diversity in maize implies that it has had a historically large population size. On the other hand, the high degree of morphological divergence between maize and its wild ancestors suggests that maize underwent selection for morphological traits. In other words, the morphological divergence between maize and its wild ancestors suggests that maize experienced a domestication bottleneck.
Investigation of a domestication bottleneck in maize requires some knowledge of genetic diversity in its wild relatives. Here we focus on two wild relatives in the genus Zea: Z. mays ssp. parviglumis (hereafter also called “parviglumis”) and Z. luxurians. Parviglumis is thought to be the progenitor of maize (4); current hypotheses propose that maize was domesticated from parviglumis somewhere in southern or central Mexico ≈7,500 years ago (11). Z. luxurians is a wild annual that is a distant relative within the genus (12). We focus on Z. luxurians to gain better insight into the genetic history of the genus as a whole.
Because most crops were domesticated around 10,000 years ago, the study of domestication bottlenecks requires an approach that is capable of making inferences about past events. Coalescent theory (13) provides a population genetic framework for inferring past events, because it utilizes the historical information accrued in DNA sequences. A great deal of effort has been expended in using DNA sequences and the coalescent framework to detect and quantify past selection events (14–16). Similar approaches can also be used to investigate population bottlenecks (17–19).
The purpose of this study is to further explore genetic diversity in maize and its wild relatives, with the goal of better understanding the genetic consequences of domestication bottlenecks. To address these issues, we have sampled DNA sequences from the Adh1 locus of 19 individuals representing maize, parviglumis, and Z. luxurians. The Adh1 sequences have been used to: (i) compare genetic diversity in the three Zea taxa, (ii) assess genetic relationships among the taxa, and (iii) guide coalescent investigations of a bottleneck associated with maize domestication, with the explicit goal of exploring potential founding population sizes of maize.
MATERIALS AND METHODS
Sampling DNA Sequences.
We PCR-amplified a 1,400-bp portion of the Adh1 gene from 19 Zea individuals, including four maize individuals, seven Z. luxurians individuals, eight parviglumis individuals, and one Tripsacum dactyloides individual (Table 1). The Adh1 gene was amplified with Taq polymerase by using primers specific to the 4th and 10th exons of the gene (8). PCR consisted of 30 cycles of 1′ 94C, 1′ 55C, and 2′ 72 C. Amplified products were cloned into pGEM-T and sequenced with T7 polymerase on a Pharmacia ALFexpress automated sequencer. These 19 sequences were aligned with 5 previously published maize Adh1 sequences (Table 1).
Table 1.
Individual and Adh1 sequences sampled in this study
| Taxon | Land race or accession no. | Location | Source | Sequence abbreviation |
|---|---|---|---|---|
| Maize | Corn Belt Dent | USA | Ref. 48 | Fast |
| Corn Belt Dent | USA | Ref. 49 | Slow | |
| Araguito | Lowland Venezuala | Goodman* | Arag | |
| Chococeno | Colombia | Goodman | Choc | |
| Conico | Mexico | Goodman | Coni | |
| Coroico | Amazon basin | Goodman | Coro | |
| Nal-tel | Mexico | Goodman | Nal | |
| Pollo | Andean Mountains | Goodman | Poll | |
| Tuxpeno | Mexico | Goodman | Tuxp | |
| Zea mays ssp. parviglumis | 331785† | Michoacon, Mexico | USDA-ARS‡ | Parv1a |
| 331785† | Michoacan, Mexico | USDA-ARS | Parv1b | |
| 331786 | Mexico, Mexico | USDA-ARS | Parv2 | |
| 384061 | Guerrero, Mexico | USDA-ARS | Parv3 | |
| 384064 | Guerrero, Mexico | USDA-ARS | Parv4 | |
| M046 | Jalisco, Mexico | Doebley§ | Parv5 | |
| M063 | Guerrero, Mexico | Doebley | Parv6 | |
| M106 | Guerrero, Mexico | Doebley | Parv7 | |
| Zea luxurians | 21863 | Guatemala | USDA-ARS | Lux1 |
| 21866 | Guatemala | USDA-ARS | Lux2 | |
| 21879 | Chiquimula, Guatemala | USDA-ARS | Lux3 | |
| 21893 | Chinandega, Nicaragua | USDA-ARS | Lux4 | |
| 306615 | Jutiapa, Guatemala | USDA-ARS | Lux5 | |
| 311282 | Chiquimula, Guatemala | USDA-ARS | Lux6 | |
| M018 | Chiquimula, Guatemala | Doebley | Lux7 | |
| Tripsacum dactyloides | Trip1459 | LaGrange, Texas | deWald¶ | Trip |
M. M. Goodman, North Carolina State University, Raleigh.
Both alleles were sequenced from this heterozygous individual.
U. S. Department of Agriculture Agricultural Research Station, Iowa State University, Ames.
J. F. Doebley, University of Minnesota.
C. deWald, USDA-ARS, Woodward, OK.
Many of the 19 new Adh1 sequences contained “singletons,” a single base-pair change relative to the remainder of the sequences. Singletons can either represent true sequence variation or Taq polymerase artifact. (In contrast, polymorphisms shared among more than one sequence have a negligible probability of being produced by Taq polymerase error.) We investigated the verity of singletons by reamplifying and resequencing the appropriate Adh1 allele from all 19 Zea individuals. Half (13 of 26) of the original singletons were the result of Taq polymerase error. We corrected these Taq artifacts and estimated that Taq error occurred at a frequency of roughly 1 in 1,500 bp. We were unable to verify four silent singletons from three previously published maize sequences (8). We included these unverified singletons in analyses, but our results do not vary qualitatively when they are excluded.
Data Analysis.
We used the measure θ̂ = S/an−1 to summarize genetic diversity, where S is the number of segregating sites, an−1 = Σi=1n−1 1/i, and n is the number of sampled sequences. Under neutral equilibrium evolution, θ̂ is an unbiased estimator of the population parameter θ = 4Nμ, where N is the population size and μ is the mutation rate (13, 20). We considered only silent sites in our tabulation of S; silent sites were defined as third-position and intron sites.
Phylogenetic reconstruction was based on the neighbor-joining method (21) with Kimura two-parameter distances (22), and we assessed confidence by using 1,000 bootstrap replicates. The minimum number of recombination events in a sample of sequences was estimated by the method of Hudson and Kaplan (23), as implemented in sites (24).
We tested for departures from neutrality by using the tests of Sawyer et al. (25), MacDonald and Kreitman (15), and Tajima (26). The test of Sawyer et al. compares the frequency distributions at different types of polymorphic sites. We compared the frequency distributions of nonsynonymous, synonymous, and intron polymorphism with each other by using Kruskal–Wallace and Mann–Whitney tests (27). We treated parviglumis and maize as a single population for these tests, because the test is likely to be most powerful when there are many alleles. We applied the McDonald–Kreitman test to nonsynonymous, synonymous, and intron site variation by using a single Adh1 sequence from T. dactyloides as an outgroup. Tajima’s test was applied to total variation and silent site variation.
Coalescent Simulations.
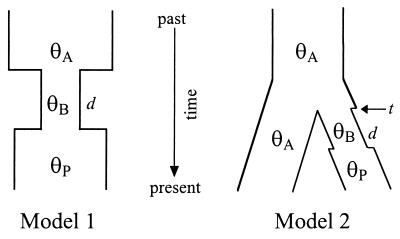
We used computer simulations of the coalescent process to investigate population sizes during a bottleneck associated with domestication (13, 28). The simulations were based on two different models, which are represented in Fig. 1. In both models it was assumed that there was a reduction in population size associated with the initial domestication of maize and that the population size increased after maize was widely cultivated and distributed.
Figure 1.
Schematic representation of the coalescent models used in simulation. See text for details.
The first model represents a single population that has undergone two instantaneous changes in population size, corresponding to the beginning and the end of a domestication bottleneck. For this model, d represents the duration in generations of the bottleneck, and θA, θB, and θP represent θ for the ancestral population, the population during the domestication bottleneck, and the present population, respectively. For given values of θA, θP, and d, we varied θB so that either: (i) the mean S from 10,000 simulations was within ±0.20 of Smaize or (ii) 97.5% (±0.2%) of 10,000 simulations had smaller S than Smaize. In this way, we estimated the expected value and the 95% lower confidence interval of θB, conditional on d, θA, θP, and Smaize. The 95% lower confidence interval of θB represents the minimum estimate of θB that is statistically consistent with the observed data.
The second model represents two populations, one of which has experienced a domestication bottleneck (Fig. 1). This model contains five parameters of interest: d, the duration of the bottleneck; t, the time the two populations diverged; θA, the population parameter of both the ancestral population and the nonbottlenecked population; θB, the population parameter during the bottleneck; and θP, the current θ of the population that experienced a bottleneck. This model assumes that divergence between populations was rapid, with no gene flow following population divergence. The expected value and lower 95% confidence interval of θB was estimated as in model I except that the number of polymorphisms shared between populations (R), rather than the number of segregating sites S, was compared between observed and simulated data. In short, the two coalescent models employ different summary statistics from DNA sequence data to make inferences about θB.
For both models, Tajima’s D (26) was used as a measure of “goodness-of-fit” between the coalescent model and the observed data. In all simulations, D from observed data was compared with the distribution of D based on simulated data. If the observed D did not fall within the central 95% of the distribution of D, we concluded that the observed data did not fit the coalescent model, given the parameter values used for simulation. All simulations were based on 997 silent sites and sample sizes of 9 for the bottlenecked population (representing maize) and 8 for the nonbottlenecked population (representing the ancestor parviglumis).
RESULTS
Summary of Adh1 Sequence Variation.
Table 2 contains a summary of sequence variation found in the three Zea taxa. As measured by θ̂, Z. mays ssp. parviglumis is the most diverse of the three taxa at the Adh1 locus (Table 2). Furthermore, parviglumis sequences are distributed widely on the genealogy (Fig. 2). One subset of parviglumis sequences forms a monophyletic clade that is an outgroup to the remainder of the Zea Adh1 sequences. This group contains sequences 1b, 4, 5, and 7, and two of these sequences are identical (sequences 4 and 7). The remaining parviglumis sequences (haplotypes 1a, 2, 3, and 6) do not form a distinct clade. It should be noted that there is no clear relationship between genealogical relationships (as inferred from Fig. 2) and geographic origin. For example, sequences parv1a and parv1b came from the same individual, but one sequence is within the monophyletic outgroup clade and the other is not. It should also be noted that recombination is detectable among parviglumis Adh1 sequences (Table 2), and recombination may affect phylogenetic resolution. Nonetheless, the wide distribution of parviglumis alleles on the Adh1 genealogy, coupled with the observation that parviglumis is genetically diverse, is consistent with a historically large population segregating old alleles.
Table 2.
Variation at the Adh1 locus
| Taxa | n | m | S | θ̂ | θ̂/bp | D | r |
|---|---|---|---|---|---|---|---|
| parv | 8 | 993 | 63(1) | 24.30 | 0.0245 | −0.241 | 4 |
| maize | 9 | 997 | 49(1) | 18.03 | 0.0181 | 0.785 | 3 |
| lux | 7 | 998 | 26(0) | 10.61 | 0.0106 | 0.258 | 3 |
| all | 24 | 998 | 94(2) | 25.17 | 0.0252 | 0.241 | 6 |
n, number of sequences; m, number of silent sites; S, number of segregating silent sites (with number of segregating replacement sites in parentheses); D, tajima’s D, based on silent sites; r, the minimum number of inferred recombination events among sequences.
Figure 2.
The neighbor-joining reconstruction of Adh1 sequences. Bootstrap values greater than 50% are given above nodes. Abbreviations are given in Table 1.
Sequence diversity at the Adh1 locus is consistent with a cultivar–progenitor relationship between maize and parviglumis, for three reasons. First, maize contains less sequence diversity than parviglumis (Table 2). However, the reduction in diversity is not severe: maize contains roughly 75% of the level of genetic diversity found in parviglumis at the Adh1 locus. Second, maize and parviglumis contain a relatively high number of shared polymorphisms (r = 35, of a total of 49 segregating sites in maize), suggesting a recent divergence between taxa. Finally, the Adh1 genealogy suggests that maize sequences represent a subset of parviglumis sequences (Fig. 2).
Patterns of sequence diversity in Z. luxurians differ considerably from those found in parviglumis. For example, Z. luxurians contains the least sequence variation at the Adh1 locus, with roughly 60% of the sequence variation found in maize (Table 2). Furthermore, phylogenetic reconstruction of Adh1 sequences indicates that Z. luxurians sequences form a highly supported monophyletic clade that is distinct from parviglumis and maize sequences (Fig. 2). Finally, Z. luxurians shares relatively few polymorphisms with either parviglumis (r = 11) or maize (r = 9).
Tests of Neutrality.
If we are to make reliable demographic inferences about domestication bottlenecks from Adh1 data, it is important that genetic variation at the Adh1 locus is not affected by selection, either directly or indirectly (i.e., through linkage to selected loci). We used two methods to test for the direct action of selection. First, we compared the frequency distributions of nonsynonymous, synonymous, and intron polymorphisms segregating in maize and parviglumis. If the variation is neutral, the frequency distributions of mutations at the different types of site should be the same (25). There is no evidence that the frequency distributions are different either between all three types of polymorphism (P = 0.88), between silent and nonsilent polymorphisms (P = 0.64), or between synonymous and intron polymorphisms (P = 0.86). Thus, we cannot detect deviation from the null hypothesis of neutrality. Second, we performed MacDonald–Kreitman tests (15). There is no evidence of a departure from neutrality between the variation at nonsynonymous, synonymous, and intron site substitutions (χ2 = 1.84, df = 2, P = 0.40) or between any pair of categories (data not shown). Finally, we used Tajima’s method (26) to test for indirect or direct effects of selection, and there was no evidence of a departure from the equilibrium neutral model whether all sites were considered or just silent sites (Table 2). The statistical power of these tests for neutrality is probably low (19), but we do not detect any departures from neutral evolution.
Coalescent Simulations.
Assumptions. In this section, we use simulations of the coalescent process to estimate θB, the population parameter during a domestication bottleneck (Fig. 1). In these simulations we make the explicit assumption that maize experienced a bottleneck associated with domestication, and we also make the assumption, consistent with our tests of neutrality, that variation at the Adh1 locus is neutral. We further assume that a domestication bottleneck first occurred 7,500 generations in the past, which corresponds with the time of maize domestication (11). For the two-population model the divergence time t is also assumed to be 7,500 generations.
If parviglumis is the progenitor to maize, then θ̂parv provides an estimate of θA (Fig. 1). We thus assume θA = 24.30 for simulations under both models (Table 2). We cannot use θ̂maize as an estimate of θP, because maize probably has not evolved according to the assumptions of the equilibrium neutral model. We thus explore a range of values for θP in simulations.
The one-population model.
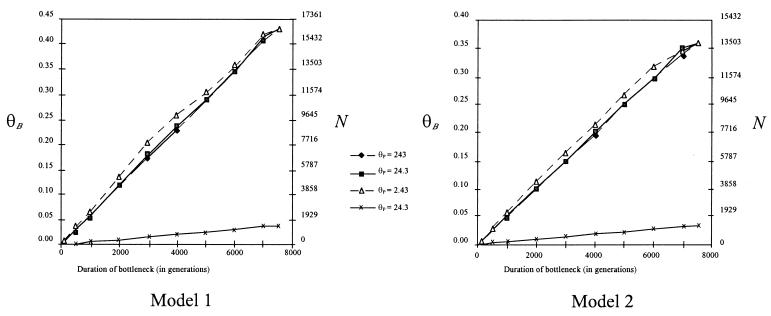
Under the one-population model (Fig. 1), we used Smaize as a summary statistic to estimate θB. The results of simulations are given in Fig. 3. Four features of the simulations deserve comment. First, the results do not have strong dependence on θP, even when θP differs by two orders of magnitude. The lack of strong dependence on θP reflects the fact that the domestication event is evolutionarily recent and further indicates that our results are not strongly dependent on accurate inference of the current θ of maize. Second, d and θB are positively correlated and have a linear relationship over much of the parameter space. This relationship is intuitive: If a bottleneck is of long duration, then the bottleneck population size must be commensurately large to maintain genetic variation. Third, data from simulations are consistent with observed data from maize, as measured by Tajima’s D. For the parameter values graphed in Fig. 3, Dmaize fell within the central 95% of the distribution of D in every case. This suggests that the frequency distribution of polymorphisms from simulated data is similar to that from observed data, although it should be noted that we do not know the power of Tajima’s D as a goodness-of-fit statistic.
Figure 3.
Results of simulations based on model 1 and model 2. The right-hand y-axis of both graphs represents the population size N; N is calculated from θ assuming a mutation rate of 6.5 × 10−9 mutations per nucleotide site per year (29) over 997 nucleotide sites. For each graph, the top three lines represent estimates of θB based on different parameter values for d and θP. For ease of presentation, symbols are removed where lines overlap. The lowest plotted line represents estimates of lower 95% confidence of θB for θP = 24.3. This last line was nearly indistinguishable from lower 95% confidence intervals estimated with θP = 243 and θP = 2.43.
Finally, and most importantly, estimates of θB can be used to estimate the size of the population during a domestication bottleneck (Fig. 3). To estimate the population size N, we assume that μ per site is equal to the average substitution rate of 6.5 × 10−9 substitutions per synonymous site per year at grass Adh loci (29) over 997 silent sites.
Estimates of N provide insight into the number of individuals that may have been involved in a domestication event. For example, if the domestication bottleneck was 10 generations in length, we estimate that the domestication of maize was based on 23 parviglumis individuals, with a lower bound estimate of ≈2.0 individuals. For a bottleneck of 500 generations, we estimate that domesticated maize is based on a population of roughly 1,157 individuals, with a minimum size of 100 individuals. A bottleneck duration of 7,500 generations, which represents a bottleneck from the original time of domestication to the present, corresponds to a population size of 16,588 individuals, with a 97.5% lower bound of 1,466 individuals.
Two-population model.
A similar but alternative way to estimate θB is to use shared polymorphisms R, rather than segregating sites S, as a summary statistic. The use of R as a statistic has the advantage that it summarizes information about polymorphisms that arose before the split of the populations in question—that is, R is not affected by recent mutation events. Furthermore, R, unlike S, does not depend on singletons and thus is less sensitive to sequencing error. We simulated data under the two-population model (Fig. 1, model 2) by using the suite of parameter values that were employed in one-population simulations, and we compared R between simulated and real data to estimate θB.
Estimates of θB from two-population simulations are quite similar to those from the one-population simulations (Fig. 3). For example, a population bottleneck of 10 generations in duration is estimated to be 20 individuals (lower bound: 1.74 individuals). The estimate of the population size for a bottleneck of 7,500 generations duration is 13,887 individuals (lower bound: 1,350 individuals). Observed values of D fit the simulated distribution of D for all parameter values reported in Fig. 3; this is true whether D is calculated just within population 1 (which represents parviglumis), just within population 2 (which represents maize), or over both populations. Thus, as measured by D, our simulation results are consistent with the observed data.
DISCUSSION
It has long been known that maize is genetically diverse, and myriad measures attest to high genetic variation within maize (4–10). Superficially, these observations imply that maize has had a historically large population size. In contrast, the high degree of morphological divergence between maize and its wild relatives suggests that maize underwent selection for agronomic traits, which should have been accompanied by a strong domestication bottleneck. The purpose of this study is to address this apparent contradiction by gaining insight into the dynamics of domestication bottlenecks.
The Domestication Bottleneck of Maize.
Computer simulations demonstrate that the full complement of sequence diversity currently found in maize Adh1 can be explained by a founding population of a very few parviglumis individuals. For example, we estimate with the two-population model that a domestication bottleneck of 10 generations would have contained ≈20 individuals. A shorter population bottleneck suggests an even smaller founding population, i.e., a bottleneck of 5 generations contained ≈10 individuals. The important take-home message of this work is that sequence diversity in maize is consistent with a very small founder population of only a handful of individuals representing a very diverse progenitor. This finding is in agreement with that of Nei et al. (30), who showed that substantial genetic variation can remain after a founder event of very few individuals when the rate of population growth is high.
Our simulations show that the size of the founder population depends on the duration of the domestication event, but little is known about the duration of maize domestication. Archeological evidence suggests that the domestication of eikhorn wheat required at most a few centuries (31). If maize domestication proceeded at a similar rate (i.e., 300 years), then a bottleneck population size of 586 parviglumis individuals is sufficient to explain the sequence diversity found in maize Adh1.
Alternatively, we can estimate the maximum duration of a domestication bottleneck by assuming that its duration was bounded by the time of the original domestication of maize in southern or central Mexico and the time of the eventual distribution of maize to other regions. It has been estimated that the original domestication event occurred 7,500 years ago (11), and archaeologists estimate that maize was introduced to other regions (the Tehuacan caves) as early as 4,700 years ago (32). Based on this evidence, the maximum duration of the domestication bottleneck is 7,500 − 4,700 = 2,800 years. [This estimate is probably an overestimate of the true duration of any bottleneck associated with the initial steps of maize domestication, for two reasons. First, the fossil record is sparse and thus it is difficult to detect the earliest geographic distribution of maize. Second, some scholars believe maize may have been domesticated more recently than 7,500 years before present (33).] A domestication bottleneck of 2,800 years in duration corresponds to a population of roughly 5,600 individuals, based on the two-population model.
It is interesting to compare the population size during domestication to the population size of parviglumis. We estimate θparv to be 24.30 (Table 2). Under the equilibrium neutral model and assuming a neutral mutation rate for Adh1 (29), this suggests a long-term population size of ≈940,000 individuals. If the domestication bottleneck consisted of 5,600 individuals, then the founder population of maize represented a mere 6.0% of the long-term population size of parviglumis. This percentage emphasizes that the germplasm of maize could be based on a population that was only a small fraction of that of its wild ancestor.
In short, we do not and cannot know the duration of the maize domestication bottleneck. However, our studies have shown that a few to a few hundred parviglumis individuals were sufficient to capture the amount of genetic diversity found in the Adh1 locus of maize.
Sequence Diversity in Wild Zea Taxa.
These results are not entirely intuitive. How can such a potentially small founding population lead to such a diverse crop? The answer lies, in part, with the incredible sequence diversity of parviglumis. Sequence diversity at the Adh1 locus in parviglumis is higher than sequence diversity at the Adh locus of any plant sampled to date, including pearl millet (34), Arabidopsis thaliana (35), Arabis gemmifera (36), and Z. luxurians, and is also more diverse than loci in several Drosophila sps. (16, 37) and humans (38). Given this highly diverse progenitor, a short domestication event based on a handful of heterozygous individuals could result in a high level of sequence diversity. One must also consider that recombination and transposition have contributed to genetic diversity within maize after its domestication; here we are concerned with the variation contributing to domestication.
The high diversity of parviglumis does not appear to be a general feature of the genus Zea, however. Sequence diversity in Z. luxurians is lower than sequence diversity in either parviglumis or maize, and phylogenetic reconstruction suggests that Z. luxurians sequences share a most recent common ancestor in exclusion to either parviglumis or maize sequences. Based on the net sequence divergence between Z. luxurians and parviglumis sequences (39), we estimate that Z. luxurians and parviglumis separated roughly 1.02 million years ago, suggesting a substantial history of independence between Z. luxurians and parviglumis. This history of independence may not hold at all loci, however, because a previous study indicated that a Z. luxurians and a maize individual contained identical DNA sequences at the c1 locus (40). The differences between Adh1 and c1 data may be due to selection at the c1 locus (40) but merit further study. In general, our observations are consistent with isozyme studies that have shown Z. luxurians to be the least diverse member of the genus Zea (4).
Examining Methods and Assumptions.
Our inferences about the size of populations during a domestication bottleneck rely on coalescent models. Coalescent models are simple approximations of complex processes, and hence it is important to examine the assumptions of the models. First, the models assume neutrality and random mating. There is no strong evidence for deviation from the former with Adh1 data, but the initial stages of domestication may have violated the latter assumption to some unknown degree.
Second, the models assume instantaneous changes in population sizes. Nei et al. (41) has shown that the amount of genetic diversity retained in a founder population depends on the rate of growth of the population, and hence models with noninstantaneous shifts in population sizes might be more informative. However, our simulations show a lack of strong dependence on θP, which suggests that instantaneous time-change assumptions are not of great consequence in this case.
Third, the coalescent models do not include recombination. The inclusion of recombination in our simulations would not affect our estimates of θB, but recombination would reduce the 95% confidence limits on θB. For this reason, our lower 95% confidence limits on θB are probably underestimates (Fig. 2). The upper bound on θB would decrease with recombination. Without recombination, the upper bound on θB is undefined (data not shown), so we cannot currently reject hypotheses that posit a very large founding population size.
Fourth, the models implicitly assume that ancestral and bottlenecked populations did not exchange genetic resources; in other words, the models assume that there was no introgression between parviglumis and the incipient maize crop. This is not an accurate assumption, because some cross-hybridization between the new domesticate and its wild ancestor must have occurred. However, that maize could be based on very few parviglumis individuals suggests that introgression need not have been frequent to explain the origin of maize. This observation provides an alternative to arguments that reciprocal introgression between maize and its wild ancestors has been important (42).
Fifth, we assume that θ̂parv accurately reflects θA, the population parameter of the ancestral population. This assumption is subject to the criticism that maize may have resulted from a hybridization event, in which case parviglumis may not be the ancestor to maize. Historically, these hybridization theories have had strong proponents (43, 44), but most of these theories have been discounted by molecular data (45). One remaining notion is that T. dactyloides hybridized with a perennial Zea sp. to produce modern maize (46). Under this hypothesis, maize sequences should cluster phylogenetically with T. dactyloides sequences. Such clustering is not evident in our data (Fig. 2), and thus we find no evidence for T. dactyloides hybridization with Zea at the Adh1 locus. Our data do not permit a general and explicit test of the hypothesis that parviglumis is the progenitor to maize, but the data are consistent with this hypothesis.
Finally, it must be cautioned that our results are based only on sequence diversity at the Adh1 locus. Population bottlenecks should affect all loci within a genome, and inferences about domestication bottlenecks ideally should be based on multiple loci. We can report, however, that data from the glb1 locus provides similar estimates of genetic diversity in maize, Z. luxurians, and parviglumis, and these data also yield similar inferences about the size of a domestication bottleneck (H.H. and B.S.G., unpublished data).
Significance.
We have assessed sequence diversity between a crop and its wild ancestors at a presumably neutral locus, and we have used sequence information to explore the potential size and duration of a domestication bottleneck. These explorations reveal that maize, despite its high genetic diversity, could have been founded on a very small population of a very diverse progenitor. These results have import for understanding the domestication of maize. Recent quantitative genetic studies have shown that the morphological differences between maize and its wild relatives may be attributable to as few as five loci (47). It is possible that the domestication of maize was based on crossing the individuals that contained the appropriate alleles at these five loci to a small, additional number of wild individuals, with continued selection for morphological traits. Although our study cannot reject more complex scenarios involving hybridization, introgression, and large population sizes, this simple scenario is sufficient to explain both the morphological divergence of maize and the extent of sequence diversity within maize.
Acknowledgments
We thank J. Wakeley, S. V. Muse, M. Millard, C. DeWald, J. Doebley, J. Hey, and four anonymous reviewers for assistance or comments. This work was supported by a U.S. Department of Agriculture grant to B.S.G.
Footnotes
References
- 1.Tanksley S D, McCouch S R. Science. 1997;277:1063–1066. doi: 10.1126/science.277.5329.1063. [DOI] [PubMed] [Google Scholar]
- 2.Goodman M M. J Hered. 1990;81:11–16. doi: 10.1093/oxfordjournals.jhered.a110919. [DOI] [PubMed] [Google Scholar]
- 3.Xiao J H, Grandillo S, Ahn S N, McCouch S R, Tanksley S D, Li J, Yuan L. Nature (London) 1996;384:223–224. [Google Scholar]
- 4.Doebley J, Goodman M M, Stuber C W. Syst Bot. 1984;9:203–218. [Google Scholar]
- 5.Doebley J F, Renfroe W, Blanton A. Genetics. 1987;117:139–147. doi: 10.1093/genetics/117.1.139. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.McClintock B. In: Maize Breeding and Genetics. Walden D B, editor. New York: Wiley; 1978. pp. 159–184. [Google Scholar]
- 7.Buckler E S, Holtsford T P. Mol Biol Evol. 1996;13:612–622. doi: 10.1093/oxfordjournals.molbev.a025621. [DOI] [PubMed] [Google Scholar]
- 8.Gaut B S, Clegg M T. Proc Natl Acad Sci USA. 1993;90:5095–5099. doi: 10.1073/pnas.90.11.5095. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Shattuck-Eidens D M, Bell R N, Neuhausen S L, Helentjaris T. Genetics. 1990;126:207–217. doi: 10.1093/genetics/126.1.207. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Goloubinoff P, Paabo S, Wilson A C. Proc Natl Acad Sci USA. 1993;90:1997–2001. doi: 10.1073/pnas.90.5.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Iltis H H. Science. 1983;222:886–894. doi: 10.1126/science.222.4626.886. [DOI] [PubMed] [Google Scholar]
- 12.Doebley J. Maydica. 1990;35:143–150. [Google Scholar]
- 13.Hudson R R. Oxf Surv Evol Biol. 1991;7:1–44. [Google Scholar]
- 14.Kreitman M, Hudson R R. Genetics. 1991;127:565–582. doi: 10.1093/genetics/127.3.565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.McDonald J H, Kreitman M. Nature (London) 1991;351:652–654. doi: 10.1038/351652a0. [DOI] [PubMed] [Google Scholar]
- 16.Hilton H, Kliman R M, Hey J. Evolution. 1994;48:1900–1913. doi: 10.1111/j.1558-5646.1994.tb02222.x. [DOI] [PubMed] [Google Scholar]
- 17.Tajima F. Genetics. 1989;123:597–601. doi: 10.1093/genetics/123.3.597. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tajima F. In: Mechanisms of Molecular Evolution. Takahata N, Clark A, editors. Tokyo: Japan Scientific Societies Press; 1993. pp. 37–60. [Google Scholar]
- 19.Simonsen K L, Churchill G A, Aquadro C F. Genetics. 1995;141:413–429. doi: 10.1093/genetics/141.1.413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Watterson G A. Theor Pop Biol. 1975;7:188–193. doi: 10.1016/0040-5809(75)90020-9. [DOI] [PubMed] [Google Scholar]
- 21.Saitou N, Nei M. Mol Biol Evol. 1987;4:406–425. doi: 10.1093/oxfordjournals.molbev.a040454. [DOI] [PubMed] [Google Scholar]
- 22.Kimura M. J Mol Evol. 1980;16:111–120. doi: 10.1007/BF01731581. [DOI] [PubMed] [Google Scholar]
- 23.Hudson R R, Kaplan N L. Genetics. 1985;111:147–164. doi: 10.1093/genetics/111.1.147. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Hey J, Wakeley J. Genetics. 1997;145:833–846. doi: 10.1093/genetics/145.3.833. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Sawyer S A, Dykhuizen D E, Hartl D L. Proc Natl Acad Sci USA. 1987;84:6225–6228. doi: 10.1073/pnas.84.17.6225. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Tajima F. Genetics. 1989;123:585–595. doi: 10.1093/genetics/123.3.585. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Sokal R R, Rholf F J. Biometry. New York: Freeman; 1995. [Google Scholar]
- 28.Wakeley J, Hey J. Genetics. 1997;145:847–855. doi: 10.1093/genetics/145.3.847. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Gaut B S, Morton B R, McCaig B M, Clegg M T. Proc Natl Acad Sci USA. 1996;93:10274–10279. doi: 10.1073/pnas.93.19.10274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nei M, Maryuma T, Chakraborty R. Evolution. 1975;29:1–10. doi: 10.1111/j.1558-5646.1975.tb00807.x. [DOI] [PubMed] [Google Scholar]
- 31.Diamond J. Science. 1996;278:1243–1244. [Google Scholar]
- 32.Long A, Benz B F, Donahue D J, Jull A J T, Toolin T J. Radiocarbon. 1980;31:1035–1040. [Google Scholar]
- 33.Smith B D. The Emergence of Agriculture. New York: Scientific American Library; 1995. [Google Scholar]
- 34.Gaut B S, Clegg M T. Genetics. 1993;135:1091–1097. doi: 10.1093/genetics/135.4.1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Innan H, Tajima F, Terauchi R, Miyashita N T. Genetics. 1996;143:1761–1770. doi: 10.1093/genetics/143.4.1761. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Miyashita N T, Innan H, Terauchi R. Mol Biol Evol. 1996;13:433–436. doi: 10.1093/oxfordjournals.molbev.a025603. [DOI] [PubMed] [Google Scholar]
- 37.Wang R L, Wakeley J, Hey J. Genetics. 1997;147:1091–1106. doi: 10.1093/genetics/147.3.1091. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hey J. Mol Biol Evol. 1997;14:166–172. doi: 10.1093/oxfordjournals.molbev.a025749. [DOI] [PubMed] [Google Scholar]
- 39.Nei M. Molecular Evolutionary Genetics. New York: Columbia Univ. Press; 1987. [Google Scholar]
- 40.Hanson M A, Gaut B S, Stec A O, Fuerstenberg S I, Goodman M M, Coe E H, Doebley J. Genetics. 1996;143:1395–1407. doi: 10.1093/genetics/143.3.1395. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Nei M, Maruyama T, Chakraborty R. Evolution. 1975;29:1–10. doi: 10.1111/j.1558-5646.1975.tb00807.x. [DOI] [PubMed] [Google Scholar]
- 42.Wilkes H G. Econ Bot. 1977;31:254–293. [Google Scholar]
- 43.Manglesdorf P C, Reeves R G. Proc Natl Acad Sci USA. 1938;24:303–312. doi: 10.1073/pnas.24.8.303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Wilkes H G. Crop Improv. 1979;6:1–18. [Google Scholar]
- 45.Doebley J. Econ Bot. 1990;44:6–27. [Google Scholar]
- 46.Eubanks M W. Theor Appl Genet. 1997;94:707–712. [Google Scholar]
- 47.Dorweiler J, Stec A, Kermicle J, Doebley J. Science. 1993;262:233–235. doi: 10.1126/science.262.5131.233. [DOI] [PubMed] [Google Scholar]
- 48.Sachs M M, Dennis E S, Gerlach W L, Peacock W J. Genetics. 1986;113:449–467. doi: 10.1093/genetics/113.2.449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Dennis E S, Sachs M M, Gerlach W L, Finnegan E J, Peacock W J. Nucleic Acids Res. 1984;13:727–743. doi: 10.1093/nar/13.3.727. [DOI] [PMC free article] [PubMed] [Google Scholar]