Frame Rate Considerations for Real-Time Abdominal Acoustic Radiation Force Impulse Imaging

Abstract

With the advent of real-time Acoustic Radiation Force Impulse (ARFI) imaging, elevated frame rates are both desirable and relevant from a clinical perspective. However, fundamental limitations on frame rates are imposed by thermal safety concerns related to incident radiation force pulses. Abdominal ARFI imaging utilizes a curvilinear scanning geometry that results in markedly different tissue heating patterns than those previously studied for linear arrays or mechanically-translated concave transducers. Finite Element Method (FEM) models were used to simulate these tissue heating patterns and to analyze the impact of tissue heating on frame rates available for abdominal ARFI imaging. A perfusion model was implemented to account for cooling effects due to blood flow and frame rate limitations were evaluated in the presence of normal, reduced and negligible tissue perfusions. Conventional ARFI acquisition techniques were also compared to ARFI imaging with parallel receive tracking in terms of thermal efficiency. Additionally, thermocouple measurements of transducer face temperature increases were acquired to assess the frame rate limitations imposed by cumulative heating of the imaging array. Frame rates sufficient for many abdominal imaging applications were found to be safely achievable utilizing available ARFI imaging techniques.

I. INTRODUCTION

Recently, a number of research groups have investigated acoustic radiation force-based methods for interrogating the mechanical properties of soft tissues.^1-9 Short-duration, focused radiation forces applied to tissues will induce small displacements throughout the focal region of the acoustic beam and generate shear waves with group velocities that are reflective of material shear moduli.^{1, 6, 10} The utilization of radiation force to displace target tissues raises concerns related to the thermal and mechanical safety of the technique. Many of these safety concerns have been addressed previously^{2, 6}. ^{11, 12} in the context of relatively superficial (<5 cm) focal depths and imaging geometries involving the use of electronically-translated apertures on linear arrays or mechanically-translated concave transducers.

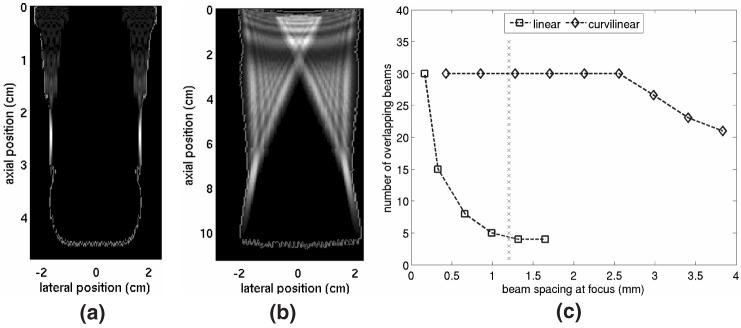
Current research in our group involves abdominal applications for acoustic radiation force impulse (ARFI) imaging.^{13, 14} Abdominal ARFI imaging is implemented using curvilinear transducers operating at relatively low (<3.5 MHz) transmit frequencies and focused as deep as 10 cm. Two-dimensional (2D) ARFI images are generated by electronically shifting the active transducer aperture between scan lines to interrogate a new region of interest. As illustrated in figure 1, the use of curvilinear scanning geometries results in a high degree of overlap between the intensity fields of radiation force beams interrogating different regions of the 2D field-of-view (FOV). Thus, markedly different spatial heating patterns are induced in abdominal ARFI compared to other radiation force imaging techniques.

FIG. 1.

Comparison of beam overlap conditions for ARFI imaging with linear and curvilinear arrays. (a) and (b) show the outline of the region of interrogation and the intensity fields of the two most outer pushing beams used to scan the region for linear and curvilinear array geometries, respectively. (c) shows the maximum number of overlapping beams in a 30 beam sequence as a function of focal beam spacing for both scanning geometries. Dotted line in (c) represents a beam spacing typical for abdominal ARFI imaging.

One consequence of the use of curvilinear arrays in abdominal ARFI imaging is the preferential deposition of energy into superficial regions of tissue. As many applications of abdominal ARFI require images to be acquired over extended periods of time, the accumulation of elevated temperatures in the near field remains a concern. For example, perceptible changes in thermal lesion size in ARFI images of liver radiofrequency ablation sites occur over a time period of about 15 s.¹⁴ As typical abdominal ablation procedures last 12-20 min, using ARFI imaging to its maximum effectiveness to monitor the entire procedure would require 50 or more data acquisitions targeted at the same region of tissue. Although previous work has examined thermal safety issues pertaining to single-frame abdominal ARFI imaging,¹⁵ safely achievable frame rates for extended imaging sessions have yet to be determined. As higher frame rates are deemed necessary, acquisition protocols may require optimization in order to address patient safety concerns with out sacrificing image quality.

There are two potential sources of thermal energy associated with ARFI imaging. First, the ultrasound pulses used to generate radiation forces deposit acoustic energy into target regions as they are absorbed by tissues. Secondly, repeated transmission of radiation force pulses can induce significant temperature rises on the face of the transducer, which will be in contact with surface tissues. Both of these effects are examined and discussed in this document. The trade-off between desired values of relevant imaging parameters (such as line density and FOV) and safely achievable frame rates is analyzed using finite element method (FEM) models. Parallel receive tracking techniques are explored as a potential method to optimize this trade-off. The role of blood perfusion as an active cooling mechanism in liver tissue is also investigated in terms of its impact on frame rates available for clinical use.

This paper is organized as follows: Section II provides a background on the thermal effects being considered and introduces basic equations and guide lines used in analysis. Section III describes the procedures used to implement the FEM thermal models and the methods used to measure transducer face heating. Section IV presents results from both the FEM model and thermocouple measurements of transducer face heating. Section V includes a summary and discussion of the results presented and their impact on safely achievable frame rates for abdominal ARFI imaging. To provide in sight into the potential clinical usefulness of abdominal ARFI imaging, some results are further analyzed in the context of liver ablation guidance.

II. BACKGROUND

Ultrasonic thermal effects

When propagating in dissipative media, acoustic waves transfer energy to the media through wave absorption. The resulting energy transfer creates a temperature flux in target tissue regions that can be estimated with the linear bio-heat transfer equation:^{15, 16}

$$\stackrel{.}{T}=\kappa {\nabla }^{2}T-\frac{T}{\tau }+\frac{q_v}{c_v}$$ (1)

where q_v is the heat-source function representing the rate of heat production per unit volume, T is the temperature relative to ambient temperature, $\stackrel{.}{T}$ is the rate of temperature change, κ is the thermal diffusivity, τ is the time constant for perfusion and c_v is the volume specific heat for tissue. The thermal diffusivity κ of a material can be related to its thermal conductivity K by:

$$K=\kappa c_v$$ (2)

For a continuous, linearly traveling plane wave, the heat-source function q_v for an ultrasound beam can be characterized by:^{15, 17}

$$q_v=\frac{\alpha p_0^2}{\rho c}=2\alpha I$$ (3)

where α is the absorption coefficient of the target tissue, ρ is the density of tissue, c is the speed of sound in tissue, p_o is the time-averaged acoustic pressure magnitude and I is the time-averaged acoustic beam intensity. The spatial distribution of q_v is dependent on transducer focal configurations and the beam sequences utilized during imaging, as well as the ultrasonic properties of the target media.

In single-frame ARFI imaging insonification times are very short (< 200 ms), and cooling due to blood perfusion is generally considered negligible. However, when calculating cumulative temperature rises associated with extended ARFI imaging sessions, blood perfusion should be included in order to retain a realistic model. The cooling effects of blood flow are incorporated into the bioheat transfer equation through the perfusion time constant:^{17, 18}

$$\tau =\frac{\rho c_v}{{\rho }_b{c}_b{w}_b}$$ (4)

where ρ_b is the density of blood, c_b is the volume specific heat of blood and w_b is the blood perfusion coefficient. In healthy hepatic tissues, w_b is estimated at 6.4 × 10^-3 s^-1.¹⁸

Transducer heating

During periods of insonification, the face of an ultrasound transducer is subject to temperature rises. These temperature increases stem from both piezoelectric inefficiencies and the absorption of acoustic energy by the lens and other materials in the transducer’s acoustic stack.¹⁹ Although these effects are usually subtle during diagnostic B-mode imaging, the longer pulse lengths used during ARFI imaging can lead to more significant temperature rises. International Electrotechnical Commission (IEC) standards limit the surface temperature of a transducer applied to a patient to 43 °C. This limitation applies when temperature measurements are made with the transducer acoustically and thermally coupled to a tissue-mimicking test object, the initial transducer face temperature is 37 °C ± 1 °C and the ambient temperature is 23 °C ± 3 °C.²⁰

ARFI imaging implementation

ARFI imaging utilizes two types of ultrasound pulses. Pushing beams are relatively long (currently up to 320 μs) in duration and are used to apply significant radiation forces to tissue. Tracking beams are used to record a reference tissue position and to monitor tissue dynamics following the application of radiation force, and are similar to conventional diagnostic B-mode imaging pulses. The tracking beams generally have pulse lengths of 1-2 wave cycles (typically equal to less than 1% of the pushing beam length). Tracking beams are also associated with low (typically ∼0.4% for abdominal applications) duty cycles and thus do not contribute significantly to tissue heating.¹² For example, using a pulse-repetition frequency (PRF) of 4.9 kHz, it would take 81.6 ms of tracking beams (400 total) to deposit the same amount of energy into tissue as a single 320 μs pushing beam. In the Sections that follow, the contributions of tracking beams to temperature rises induced in tissues are thus considered negligible.

The magnitude of temperature rise induced in soft tissue by ARFI pushing beams is related to the tissue displacement induced by the applied radiation forces. Although the relationship will vary depending on the thermal, acoustical, and mechanical properties of target tissues, a reasonable approximation is that, for a single pushing beam, a peak displacement of 5 μm will be accompanied by a peak temperature increase of 0.1 °C. If beams are fired rapidly enough to neglect heat conduction, this temperature increase will scale linearly with the number of pushing beams transmitted in the same location. The peak temperature rise induced during a 2D imaging frame is more complicated to predict and is related to the relative spatial orientations of the pushing beams used to create the image.

The conventional implementation of ARFI imaging involves transmitting pushing and tracking beams along the same line of flight to interrogate a region of tissue. Images are created by electronically translating the active transducer aperture and repeating this process in a different spatial location. A relatively new feature of ARFI imaging is the ability to incorporate parallel receive tracking, currently allowing for up to four lines of the tissue dynamic response to be recorded simultaneously after each individual pushing beam is transmitted.^{21, 22} By increasing the size of the tissue region being monitored after each pushing beam is transmitted, pushing beams can be spread further apart with little loss in overall image quality.^{14, 22} In addition to decreasing image acquisition times, the use of parallel tracking techniques in ARFI imaging dramatically reduces induced tissue heating by not only using fewer pushing beams for a given FOV but also by reducing the degree of near field overlap between intensity fields from different pushing beams.

III. METHODS

FEM model implementation

The details of FEM model implementation have been described previously.¹² In general, the spatial distribution of an ARFI pushing beam’s acoustic intensity was simulated using FIELD II, a linear acoustic field simulation soft ware program (available for download at http://www.es.oersted.dtu.dk/staff/jaj/field/).²³ Intensity data were normalized and values less than 5% of the maximum intensity were neglected to reduce computational requirements. Normalized simulation data were then scaled to have a peak intensity of 820 W/cm² at the beam focus, a value consistent with in situ values indirectly measured during ARFI imaging using an extrapolation of small-signal derated fields. Prior to incorporation into the model, the simulated and scaled intensity field was converted into a field of initial temperatures using the solution to Eq. (1) neglecting conduction and perfusion:

$$T_i=\frac{q_{v}t}{c_v}$$ (5)

where T_i is the approximated initial temperature at a point in space at the end of insonification and t is the insonification time. This method is valid for ARFI imaging since insonification times are short (<1 ms) relative to the thermal diffusivities of the tissues being modeled.¹² This field of initial temperatures from a single ARFI excitation was then superimposed on a curvilinear solid mesh created by a finite element mesh generation program (HyperMesh, Altair Computing, Inc., Troy, MI). Plane-symmetry was assumed in both the lateral and elevation dimensions.

An implicit, time-domain finite element analysis package (LS-DYNA3D, Livermore Software Technology Corporation, Livermore, CA) was used to characterize the thermal response of the modeled tissue to ARFI pushing beams. The model received the simulated initial temperature field as an input and solved for the cooling behavior associated with the tissue. Tissues were modeled as thermally homogeneous, isotropic solids. In order to simulate a continuum of tissue, the boundaries of the model were treated as insulating boundaries.¹⁷ The MATLAB software package (The MathWorks, Inc., Natick, MA) was used to determine tissue heating for 2D ARFI imaging sequences using the spatial convolution of temporally-delayed model results from a single interrogation.

Unless otherwise specified, the simulated tissues used in the FEM models of this study had thermal properties consistent with those of hepatic tissue. Tissues were modeled with a density of 1,050 kg/m³, a specific heat of 3,600 J/kg/°C and a thermal conductivity of 0.57 W/m/°C.²⁴ Literature reports indicate that the absorption coefficient (α) of hepatic tissue may range from 0.5-0.8 dB/cm/MHz^{25, 26} and thus an absorption coefficient of 0.7 dB/cm/MHz was chosen for use in this study. When simulating adipose tissue, the tissue properties assigned to models were a density of 900 kg/m³, a specific heat of 2,300 J/kg/°C and a thermal conductivity of 0.19 W/m/°C.²⁴

Tissue heating under varying frame rates was determined using custom programs written for MATLAB. As multiple ARFI frames are acquired over extended time periods, the assumption of negligible cooling due to blood perfusion is no longer valid. The effects of global perfusion were thus incorporated into FEM models predicting temperature rises over the course of many minutes. Perfusion effects lead to a global decay of thermal energy in the model, and thermal convection within the model associated with blood flow was neglected. Blood was modeled with a density of 1,000 kg/m³ and a specific heat of 4,180 J/kg/°C.¹⁸ For comparative purposes, models of tissue heating in the presence of normal (τ = 141 s),¹⁸ 50% (τ = 282 s), and negligible (τ = ∞) hepatic perfusion were implemented. Perfusion models were validated by comparing model output with the analytical solution to Eq. (1) for a spatially-uniform temperature field with no active heat sources:¹⁵

$$T=T_o\exp \left(\frac{-t}{\tau }\right)$$ (6)

where t is the time elapsed following the removal of heat sources and T_o is the temperature at time t = 0.

Models of tissue heating were validated in vitro using 36-gauge Type T thermocouples (Omega Engineering, Stamford, CT) and a 16-bit data acquisition system (SuperLogics, Waltham, MA).²⁷ Temperature rises were induced in large (12 × 12 × 10 cm) sections of bovine hepatic tissue that had been degassed in a 650 mmHg vacuum chamber for 3-4 hours and subsequently placed in a water bath. Thermocouples were centered laterally in the imaging plane and placed at depth of 5 cm, corresponding to the axial acoustic focus of the radiation force pulses used to generate the temperature rise. Twenty ARFI pulses were fired at a PRF of 50 Hz along the same line of flight, as in conventional M-mode interrogation. Each pulse had a center frequency of 2.5 MHz, a pulse duration of 160 μs, and utilized an F/2.5 focal configuration. High frequency noise in the thermocouple data was removed with a 300 sample (60 ms) running-average time domain filter. Matching FEM models were created for comparison with the experimental thermocouple data.

Transducer face heating measurements

Transducer face heating measurements were made in compliance with the measurement guidelines provided by the IEC²⁰ (briefly described in the Background Section of this paper). The only deviation from the IEC measurement protocol was that initial transducer temperatures were those associated with diagnostic B-mode imaging in the selected scanning mode (32 °C ±1.5 °C), as opposed to the those suggested by the IEC (37 °C ± 1 °C). Our experience suggests that temperature rises experienced with these lower initial transducer face temperatures will be nearly equivalent to those that would be seen with higher initial temperature values.

Measurements were made using a Siemens SONOLINE Antares™ ultrasound scanner (Siemens Medical Solutions USA, Inc., Ultrasound Division, Issaquah, WA) and a Siemens CH6-2 curvilinear array operating at 2.5 MHz. Data were recorded using Omega Engineering 36-gauge Type T thermocouples and a 16-bit SuperLogics data acquisition system. A thermocouple was placed on the center of the transducer face. ARFI data sets consisting of 10 - 40 pushing beams focused at a radial depth of 8 cm were acquired of a tissue-mimicking phantom (CIRS Corporation, Norfolk, VA) with an attenuation of 0.75 dB/cm/MHz at frame rates ranging from 0.5-0.05 Hz. Both conventional and parallel receive tracking ARFI imaging modes were utilized. Ultrasonic transmission gel was used to ensure proper acoustic coupling from the transducer to the phantom. The transducer face was allowed to return to its steady-state diagnostic B-mode imaging temperature before each ARFI acquisition sequence was initiated.

IV. RESULTS

Effect of scanning geometry

The scanning geometry utilized during ARFI imaging determines the spatial relationship between individual pushing beams used to interrogate a tissue region and thus significantly impacts both the magnitude and the spatial distribution of the resulting induced temperature changes. The FIELD II simulation package was used to quantitatively contrast the degree of beam overlap encountered in ARFI images acquired with linear and curvilinear scanning geometries. For each case, the transducer focal parameters were modeled as typically implemented clinically. Figure 1(a) illustrates the spatial characteristics of a pushing beam associated with a 4.2 MHz linear array utilizing an F/1.5 focal configuration and focused at a depth of 2.5 cm. Similar results for a 2.5 MHz curvilinear array utilizing an F/2.5 focal configuration and focused at a depth of 8 cm are shown in figure 1(b). Both figures 1(a) and 1(b) show the out line of the entire region of interrogation (imaging 5 FOV) for an imaging sequence with 30 pushing beam locations and a beam spacing of 1.2 mm in the focal region. For the curvilinear geometry, this corresponds to a beam density of 1.78 beams/degree. Figures 1(a) and 1(b) also show the normalized intensity fields associated with the two most outer pushing beams used to displace tissues in this region. In both figures 1(a) and 1(b), the transducer is located at the top of the figure and is transmitting downward.

For the focal beam spacing shown in figures (a) and (b), it is evident that near field beam overlap is much more prevalent when utilizing a curvilinear scanning geometry. The intensity fields of the outermost beams used to interrogate the FOV overlap in the curvilinear geometry while in the linear geometry they are separated by nearly 2 cm.

Figure 1(c) quantifies the amount of beam overlap associated with each scanning geometry for a range of focal beam spacings. The number of pushing beam locations (30) was held constant for each calculation and thus increasing the focal beam spacing also increased the FOV at the cost of decreasing the line density. For two beams to be considered overlapping, portions of the beams having intensity values of at least 15% of the peak single-beam intensity had to occupy the same region. The maximum number of overlapping beams for each beam spacing was then determined. Data shown for the linear array geometry are restricted to FOVs that are realistically-achievable on a transducer with a 2 cm aperture. Typical ARFI beam spacings for the linear array would be less than 0.5 mm at the focus. The vertical line at 1.2 mm indicates a typical value for beam spacing in the focal zone for abdominal ARFI imaging.

For the linear geometry, a maximum overlap of 30 beams occurs when a focal spacing of 0.165 mm is utilized. The degree of overlap drops considerably as the beam spacing is increased. When individual beams are separated by 1.3 mm at the focus, no tissue region in the FOV is insonified by more than four pushing beams. For curvilinear geometries, every beam in the sequence overlaps for focal beam spacings as large as 2.55 mm (0.83 beams/degree). Larger focal beam spacings decrease this overlap but are not practical for quality imaging if conventional ARFI acquisition techniques are utilized. However, these larger beam spacings can be realistically implemented using parallel receive tracking techniques. It should be noted that the results presented are specific to the transmit aperture sizes specified above. Smaller transmit apertures will lead to reduced beam overlap in the near field but will also result in reduced radiation force amplitude due to fewer transducer elements being utilized.

Figure 2 compares beam overlap conditions for conventional and 4-1 parallel receive ARFI imaging techniques for a curvilinear scanning geometry. The figure shows the maximum number of overlapping pushing beams in an imaging frame for each acquisition technique as a function of image FOV. Pushing beam densities were held at constant values of 1.78 and 0.45 beams/degree for the conventional and parallel receive simulations, respectively, and thus larger FOVs require the use of more total pushing beams in the imaging sequence. The density of the tracking beams used to monitor the response of tissue to the pushing beams would be identical for both acquisition techniques.

FIG. 2.

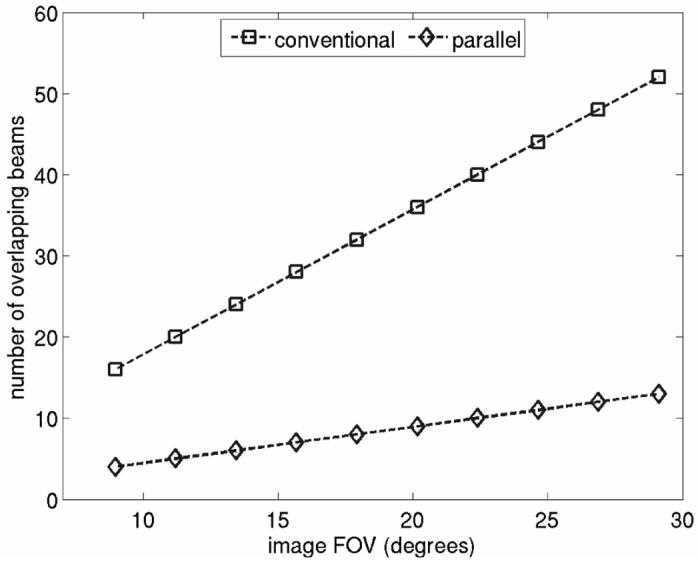
Maximum number of overlapping pushing beams vs. image FOV for conventional and parallel receive ARFI imaging. Data shown are for a curvilinear scanning geometry. Pushing beam densities were held at constant values of 1.78 and 0.45 beams/degree for the conventional and parallel receive simulations, respectively.

As shown, the utilization of parallel receive tracking techniques markedly decreases the degree of pushing beam overlap. For these focal configurations and span of FOVs, the use 4-1 parallel receive tracking techniques corresponds directly to a 4x decrease in pushing beam overlap. (For different transducer focal parameters or in media with differing attenuation characteristics, this simple relationship between pushing beam density and maximum amount of pushing beam overlap will not necessarily hold.) Figure 2 indicates that for the 29° FOV, the maximum number of overlapping pushing beams decreases by 39 when parallel receive tracking is implemented. It is also noteworthy that when using conventional acquisition techniques, there is a greater maximum beam overlap (16 beams) for the 9° FOV than there is for the 29° FOV if parallel receive techniques are utilized (13 beams). We will show in sections to come that this decrease in beam overlap will coincide with a decrease in peak temperature rises induced in tissue.

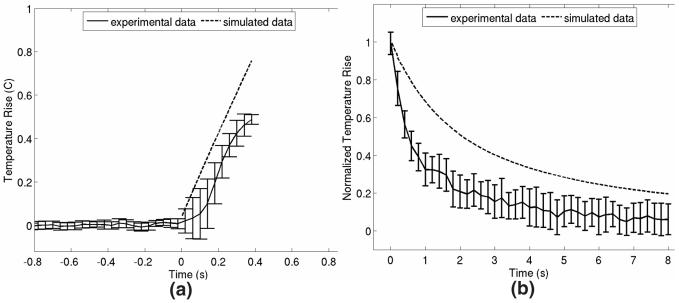
In vitro model validation

Figure 3 shows results from the in vitro experiment used to validate the thermal models that are used throughout this study. Figure 3(a) shows results comparing the simulation-predicted and experimentally-measured peak temperature rises associated with twenty 160μs ARFI pushing beams transmitted at a PRF of 50 Hz and focused at an axial depth of 5 cm. Each of the 20 beams was transmitted in an identical location. The experimental curve is the average of 12 trials, with error bars representing ±1 standard deviation from the mean. In figure 3(b), the simulated and experimentally-measured normalized cooling profiles at the focus are shown. In figure 3(a), time t = 0 corresponds to the transmission of the first pushing beam; in figure 3(b), time, t = 0 corresponds to the transmission of the final pulse of radiation force. The experimental curve is the average of 9 trials, and error bars again represent ±1 standard deviation from the mean. In both plots, the experimental data has been down-sampled to aid visualization.

FIG. 3.

Comparison of simulated predictions and experimental measurements of ARFI-induced temperature changes in bovine hepatic tissue. (a) shows tissue heating at the focus (5 cm) resulting from the transmission of 20 ARFI pushing pulses spaced temporally by 20 ms. (b) shows normalized tissue cooling at the focus immediately following the transmission of all 20 radiation force pulses. Error bars represent ±1 standard deviation at each point.

From figure 3(a), we see that the peak tissue heating predicted by the model (0.76 °C) overestimates the heating measured experimentally (∼ 0.52 °C) by about 50%. This discrepancy has many possible origins and will be discussed in further detail in the Discussion section of this paper. Additionally, in figure 3(b), the temperature rises induced in in vitro hepatic tissue appear to dissipate more quickly than as predicted by the model. This trend is consistent with previous results examining focal point cooling²⁷ and may be attributable to factors such as the greater thermal conductivity of the thermocouple relative to the neighboring hepatic tissue and the aqueous solution surrounding the tissue sample. Through out the remainder of this paper, we will take a conservative approach and assume that the temperature rises and transient behavior predicted by the model accurately reflect those encountered in in vivo hepatic tissues.

Tissue heating during ARFI imaging

Results from FEM modeling of induced heating in hepatic tissue are shown in figure 4. The beam sequence modeled consists of 40 pushing locations separated radially by 1.2 mm at the beam focus (1.78 beams/degree). All 40 pushing beams contribute to the heating pattern shown in the figure. Each individual pushing beam had a radial focus of 8 cm and a pulse length of 280 μs and was transmitted with an F/2.5 aperture. For clarity, only one half of the elevation plane data are shown.

FIG. 4.

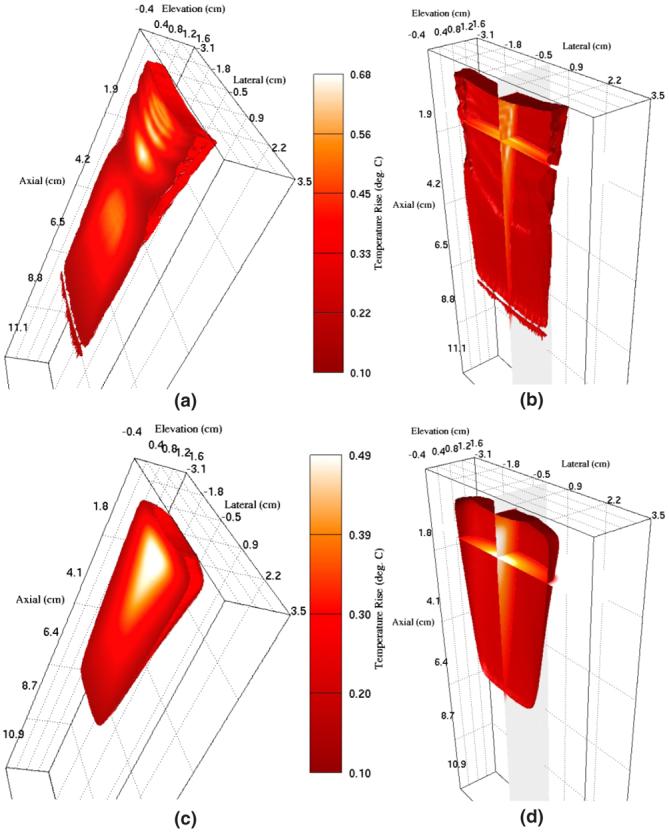
FEM simulation results showing the thermal response of hepatic tissue to a single ARFI imaging frame. (a) and (b) show results immediately following acquisition and (c) and (d) show results 15 s after acquisition. (a) and (c) show an isovolume of regions with temperatures elevated by at least 0.1 °C. (b) and (d) show isocontours of 0.1 °C as well as orthogonal slices through data.

Figures 4(a) and 4(b) show results at a time immediately following data acquisition and figures 4(c) and 4(d) show results 15 s after data acquisition has occurred. Figures 4(a) and 4(c) show an isovolume of regions with temperatures elevated by at least 0.1 °C. Figures 4(b) and 4(d) show isocontours of 0.1 °C as well as orthogonal slices through the image planes centered laterally and at a depth of 1.05 cm. Figures 4(b) and 4(d) have been shown with slightly rotated views in an effort to facilitate visualization of the extent of tissue heating into the elevation dimension.

Figure 4(a) indicates that the peak induced temperature rise associated with this beam sequence is 0.68 °C and occurs at an axial depth of 1.5 cm. Temperature rises of at least 0.1 °C extend to regions reaching 6 cm in depth and 0.6 cm in elevation. From figure 4(b) we note that temperature rises internal to the isovolume shown in figure 4(a) can be as high as 0.6 °C in the near field.

Figures 4(c) and (d) show the same region of tissue after it has been allowed to cool for 15 s without additional ARFI interrogation. At this time, residual temperature increases as large as 0.49 °C remain, with temperatures as high as 0.3 °C extending to regions as deep as 2 cm. Figure 4(d) indicates that temperatures of at least 0.3 °C extend 0.5 cm in the elevation dimension as well. Although the temperature increases shown in figure 4 are relatively minor, the time period over which significant residual temperatures can persist in the near field may lead to more significant temperature rises during multi-frame imaging sessions.

FEM models of the tissue heating that would occur when the beam sequence shown in figure 4 is transmitted 24 times over a four-minute period (0.1 Hz) into uniform hepatic tissue are shown in figure 5. Figure 5(a) and 5(b) show heating results in normally perfused tissue while figures 5(c) and 5(d) show results obtained when tissue perfusion is neglected. To ease data interpretation, the temperature maps are shown as 2D slices through the central imaging planes (each plane includes the point of highest temperature flux). Figure 5(a) and 5(c) show heating in the axial-lateral plane, centered in elevation, while figures 5(b) and 5(d) show heating in the axial-elevation plane, centered in azimuth. In figures 5(b) and 5(d), the aspect ratio of the figure has been stretched in order to aid visualization. Figure 5(e) plots the maximum temperature increase in the modeled volume after each image frame is acquired for both the perfused and non-perfused cases. In order to aid intercomparison, figures 5(c) and 5(d) are shown with the same color scale as figures 5(a) and 5(b).

FIG. 5.

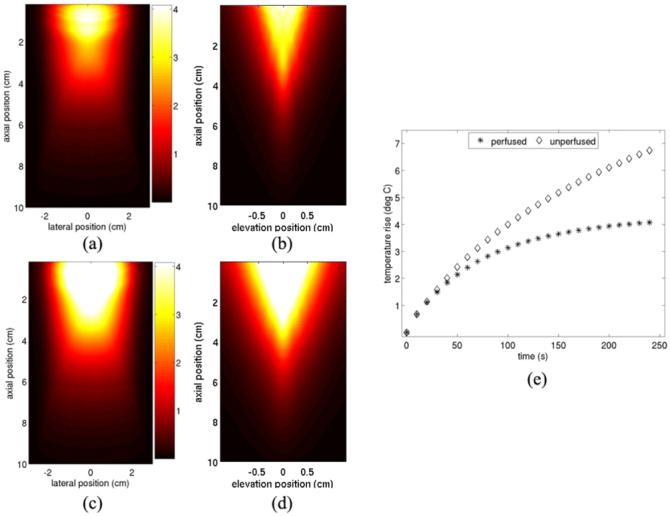
FEM models of cumulative tissue heating resulting from transmitting the sequence shown in figure 4 twenty-four times over a 4 min period. (a) and (b) show results in normally-perfused hepatic tissue. (a) shows the axial-lateral plane, centered in elevation and (b) shows the axial-elevation plane, centered in azimuth. (c) and (d) show similar images to (a) and (b), respectively, but neglect the effects of tissue perfusion. (e) shows the magnitude of peak tissue heating after every image frame is acquired for both the perfused and non-perfused cases.

From figures 5(a) and 5(b), we see that the most significant tissue heating (∼ 4 °C) resulting from many successively acquired data frames occurs primarily in the near field. However, temperature rises of 1 °C are induced at depths reaching 4.8 cm. The region of most severe temperature increase spans about 2 cm laterally and about 1 cm in elevation. Larger temperature rises (∼ 6.7 °C) are induced when perfusion is neglected (figures 5(c) and 5(d)), and temperature rises of 1 °C are now observed as deep as 5.7 cm. The data presented in figure 5(e) indicate that in the presence of global perfusion, cooling occurring between image frames will result in peak tissue temperatures approaching an equilibrium state, with tissue temperature rising less severely with each successive data acquisition. This suggests that this frame rate could be used for extended time periods with out a corresponding significant increase in induced temperature. However, when perfusion is neglected, the increase in maximum tissue temperature with each successive data acquisition remains nearly linear over the time period modeled.

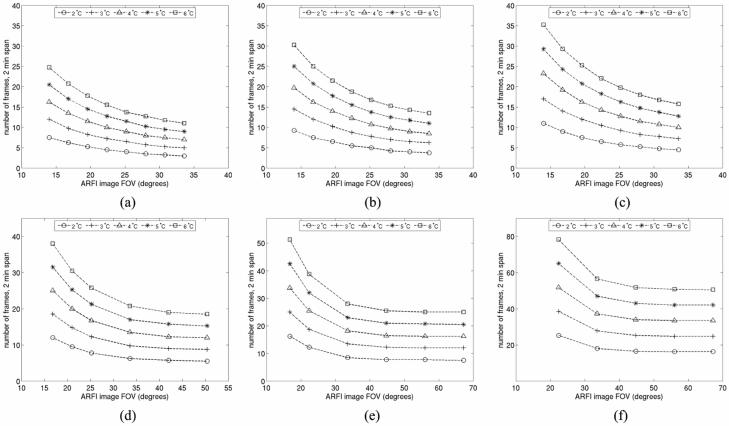
As implied by figures 1 and 2, the magnitude of the induced temperature rise in tissue during ARFI imaging is affected by both the number of pushing beam locations in the imaging sequence and the pushing beam density. Also affecting the degree of temperature rise is the frame rate utilized during extended imaging sessions. Figure 6 details the trade-off between these imaging parameters in terms of the maximum induced temperature rises in uniform hepatic tissue. To aid data interpretation, the temperature rises have been plotted relative to image FOV, which is the product of pushing beam density and the number of pushing beams used to make an image. Pushing beams were modeled with a focus of 8 cm, a pulse length of 280 μs and a transmit F/number of 2.5. Contours of constant maximum temperature rise are shown for induced heating of 2-6 °C. Due to computational requirements, only 2 min of data are shown.

FIG. 6.

FEM simulation results illustrating the trade-off between frame rate and FOV on induced tissue heating during ARFI imaging. (a) - (c) show the effects of perfusion for a given beam sequence. (a) shows results neglecting blood perfusion, (b) shows results accounting for 50% of normal blood perfusion and (c) shows results in normally perfused liver. The sequence modeled has the same pushing beam density (1.78 beams/degree) as the sequence modeled in figures 4 and 5. (d) - (f) show the effects of pushing beam density for a fixed perfusion rate of 50% of normal. (d) shows results for a conventional ARFI imaging sequence with a pushing beam density of 1.19 beams/degree. (e) and (f) show results for parallel receive tracking ARFI imaging with pushing beam densities of 0.89 and 0.45 beams/degree, respectively. Lines in the figure show contours of constant maximum temperature rise.

The top row (Figs. 6(a) - (c)) demonstrates how the effects of perfusion can alter the induced heating associated with a given frame rate and FOV for a particular beam sequence. For these three plots, the pushing beam density was held at a constant value of 1.78 beams/degree (the same as modeled in figures 4 and 5). Figure 6(a) shows results neglecting blood perfusion, figure 6(b) shows results accounting for 50% of normal blood perfusion and figure 6(c) shows results in normally-perfused hepatic tissue. As expected, when perfusion is accounted for, the safely achievable frame rate for a given FOV increases. For example, for the FOV modeled in figures 4 and 5 (22.4 degrees), if blood perfusion is neglected an ARFI data acquisition could only occur every 12 s over a 2 min span if maximum temperature rises of less than 4 °C were desired. Conversely, in normally perfused tissue, an acquisition could occur every 8.5 s over a 2 min period while remaining within the same temperature limit. Typical FOVs in conventional ARFI imaging span 20-40 degrees and thus, with this pushing beam density, acquisition rates will generally be limited to less than 10 images/min for short-term (0-2 min) imaging sessions. Cumulative heating effects will further limit frame rates during extended imaging sessions of the same tissue region.

The bottom row of figure 6 ((d) - (f)) illustrates the impact of pushing beam density on the heating contours for a fixed perfusion rate equal to 50% of the normal value. Figure 6(d) shows results for a conventional ARFI imaging sequence with a pushing beam density of 1.19 beams/degree. Figures 6(e) and (f) show results for parallel receive tracking ARFI imaging with pushing densities of 0.89 and 0.45 beams/degree, respectively.

Figures 6(d)-(f) indicate that, as expected, lower pushing beam densities allow for higher frame rates to be associated with a given FOV and temperature rise. For instance, the beam sequence simulated in figure 6(d) can interrogate a FOV spanning 33.6 degrees with 40 pushing beams, as opposed to the 60 beams needed when using the beam density simulated in figure 6(b). Thus, using the sequence in figure 6(d) would allow for a 50% increase in frame rate without a corresponding increase in induced tissue heating. The use of parallel tracking techniques allows for pushing beam densities to decrease even more drastically without sacrificing the sampling density of the tissue response to the applied force. For example, although the tracking beam density in the beam sequences of figures 6(b) and 6(f) is identical, the sequence in figure 6(f) only requires 15 pushing beams to interrogate a 33.6 degree FOV. Hence, the sequence in figure 6(f) can be transmitted every 3.2 s over 2 min for this FOV while keeping induced tissue temperatures below 4 °C, while the sequence in figure 6(b) can only be used every 14 s for 2 min under these conditions.

In many cases, adipose tissues may be present in regions where induced tissue heating is significant. Figure 7 compares the frame rate vs. FOV trade-off in hepatic and adipose tissues. Shown are contours of constant maximum temperature rise for an induced heating of 4 °C. For both curves, the beam sequence modeled represents ARFI imaging with parallel receive tracking and a pushing beam density of 0.89 beams/degree. Blood perfusion was neglected. As shown, for a given desired maximum temperature rise, achievable frame rates for imaging in adipose tissues may be nearly half those available for use in hepatic tissues.

FIG. 7.

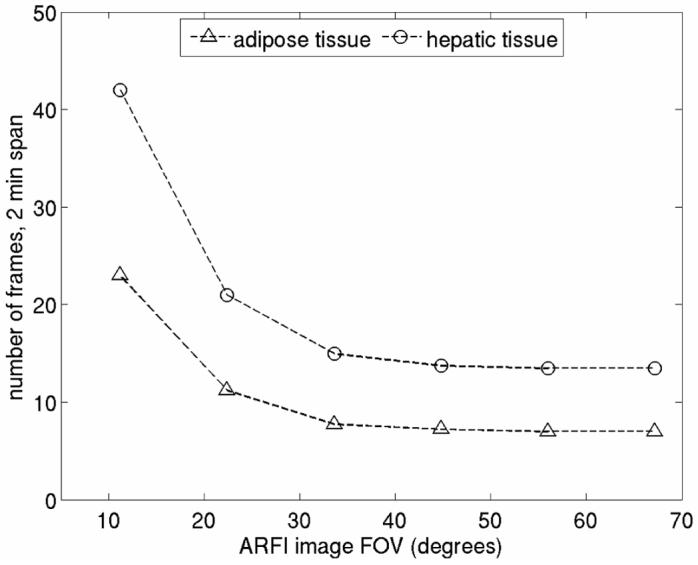
FEM simulation results illustrating the effect of tissue thermal properties on tissue heating during extended ARFI imaging. Shown are contours of constant maximum temperature rise for an induced heating of 4 °C. For both curves, the pushing beam density was 0.89 beams/degree and blood perfusion was neglected.

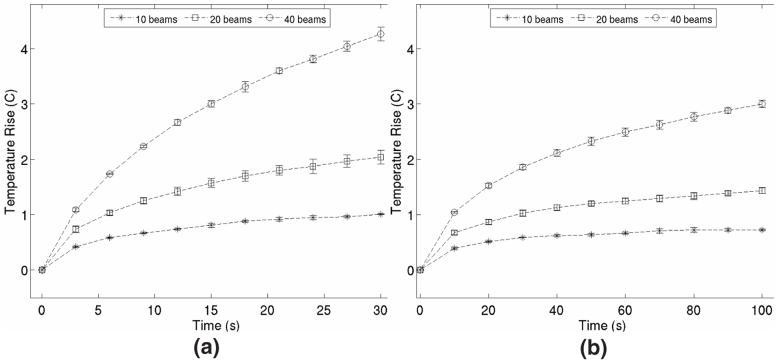
Transducer heating during ARFI imaging

Figure 8 shows results from thermocouple measurements of transducer face heating when 10 ARFI images were acquired at frame rates of (a) 0.33 Hz and (b) 0.1 Hz. Each data point in a series represents the peak temperature rise measured on the transducer face after each image frame in the sequence was acquired and is the mean value resulting from 3 trials. Error bars represent ±1 standard deviation from the mean value. Although every acquired image in the experiment had the same FOV (22.4 degrees), three different beam sequence configurations are shown for each frame rate. In each figure, the circular data series shows results generated using a conventional ARFI imaging beam sequence (the same as shown in figures 4 and 5) consisting of 40 pushing beams. The sequences used to obtain the square and star data sets used 20 and 10 pushing beams, respectively, in conjunction with parallel receive tracking techniques. Each beam sequence utilized 280 μs pushing beams focused at a radial depth of 8 cm.

FIG. 8.

Thermocouple measurements of transducer face heating during ARFI imaging. (a) shows heating pattern when 10 acquisitions are transmitted at a rate of 0.33 Hz and (b) shows heating pattern when 10 acquisitions are transmitted at a rate of 0.1 Hz. Circular data points represent results from a conventional ARFI imaging sequence consisting of 40 pushing beams. Square and star data points represent results obtained when using 20 and 10 pushing beams, respectively, in conjunction with parallel receive techniques. All images acquired during measurements had the same 22.4 degree FOV. Pushing beams had pulse lengths of 280 ms and were focused at a radial depth of 8 cm. Data points represent the average of 3 trials, error bars represent ±1 standard deviation from the mean.

In figure 8(a), we see that during conventional ARFI imaging, relatively high frame rates can lead to significant heating of the transducer face (in this case about 4.3 °C after 10 acquisitions). The temperature on the face of the transducer increases nearly linearly with number of frames acquired and extended periods of imaging at this rate with this beam sequence will likely lead to conditions unsafe both for the patient and the transducer hardware. The use of parallel receive tracking during ARFI imaging reduces the required energy flux through the transducer face needed to create an image with a particular FOV and thus results in lower transducer face temperature rises (2.0 °C and 1.0 °C for 20 and 10 pushing beams, respectively).

Given the frame rates necessary for many abdominal applications and the results provided in figure 6, the data shown in figure 8(b) likely provide a more realistic estimate for transducer face temperatures encountered in clinical settings than those presented in figure 8(a). However, even at this reduced frame rate, the temperature of the transducer face can rise more than 3 °C over a span of less than two minutes. Using parallel receive tracking techniques reduces peak transducer face temperature rises to 1.45 °C and 0.73 °C for 20 and 10 pushing beams, respectively. The effect of transducer face temperature rises on ARFI image quality is discussed in the following Section of this document.

V. DISCUSSION AND CONCLUSIONS

In this study, we used FEM models of induced hepatic tissue heating and thermocouple measurements of transducer face temperature rises to develop a framework for the design of thermally-safe abdominal ARFI imaging beam sequences. The results detailed in the previous section can be used as conservative guidelines to determine the optimal pushing beam density or imaging FOV given the frame rate requirements of a particular imaging application. As an example, to sample the radial growth of a developing thermal lesion during liver ablation surgery with ARFI, a frame rate of at least 0.07 Hz is desirable.¹⁴ Given an image FOV of 25 degrees and a pushing beam density of 1.19 beams/degree, an ARFI image can be acquired at this rate for a 2 min span without inducing peak temperature rises of more than 2 °C, even in the presence of reduced tissue perfusion. Longer temporal monitoring periods and/or applications requiring increased FOVs will induce more significant temperature rises at this frame rate and, under these operating conditions, the use of parallel receive tracking would be an attractive option. The use of parallel receive tracking techniques allows for elevated frame rates relative to conventional ARFI imaging and is particularly beneficial when large image FOVs are desired.

In conventional ARFI imaging, acquisition times and the required number of pushing beams generally limit image FOVs to sectors smaller than 50 degrees. However, with parallel receive ARFI imaging, larger imaging FOVs can be realistically achieved. An interesting feature demonstrated by figure 6(e) and 6(f) is that there is virtually no increase in induced tissue heating as FOVs grow larger than 40 degrees. With these large FOVs and reduced pushing beam densities, the outer beams used to interrogate tissues at one edge of the image will not have intensity fields that overlap those from beams interrogating tissues on the other edge of the image (see figure 1). Thus, although the size of the heated region of tissue will grow larger with increased FOV, the amplitude of the maximum temperature rise induced in the tissue region will not increase as the FOV is increased.

The thermal models in this study were generated using the same transmit frequency for both the tracking and pushing beams utilized during ARFI imaging. One mechanism for increasing the thermal efficiency of abdominal ARFI imaging without sacrificing tracking resolution would be to use a lower transmit frequency radiation force pushing pulse and then track the ensuing tissue displacements with a higher frequency beam. Lower frequency pushing pulses would encounter less near field attenuation relative to currently used pulses, and thus deposit more of their initial energy at the beam focus. This would allow for measurable displacements to be induced in target tissues with less accumulation of heat in the near field. Since beam overlap occurs primarily in the near field, the use of lower frequency pushing pulses should significantly lower the temperatures induced per ARFI imaging frame. Also due to reduced attenuation, lower transmit intensities can generally be utilized for lower frequency pushing pulses without affecting the amplitude of induced displacements in the focal region. Although an elaborate discussion of this topic is beyond the scope of this paper, this reduction in transmit intensity will generally help offset the increased likelihood of mechanical bioeffects associated with a lower transmit frequency.

There are several limitations to the thermal models used in this study. Due to computational requirements, only 2 min of FEM data were calculated for most beam sequences modeled. Although frame rate calculations over a period of 2 min will not accurately reflect temperature rises induced over much longer imaging sessions, examining trends of peak temperature rise and the spatial distribution of heating patterns over this time period allows for conservative estimates regarding acceptable long-term frame rates to be made. Another assumption inherent to our calculations is the worst-case imaging scenario of identical tissue regions in every frame. In practice, a clinician would likely be shifting the transducer between frames to examine different regions of interest within a target volume. Since peak temperature rises occur primarily away from the focus and are confined to a rather small region in the elevation plane, shifting the transducer position by 1-2 cm while readjusting the angle to maintain the same focal point will allow for extended ARFI imaging sessions of the same region with minimal additional increases in induced tissue temperatures.

For simplicity, most of the FEM thermal models presented in this manuscript describe induced temperature rises in hepatic tissue. However, other types of tissue (such as renal and adipose) are likely to been countered when scanning the abdomen. These additional varieties of abdominal tissue often have differing thermal and acoustical material properties relative to hepatic tissue and thus temperature rises induced during ARFI imaging will vary according to the constituent tissues located in the acoustic propagation path. As evidenced by figure 7, the magnitude of these temperature variations can be as large as a factor of two. Additionally, all thermal models provided in this manuscript describe pushing beams focused at a radial depth of 8 cm. Although 8 cm is a commonly used focal depth for abdominal ARFI imaging, other focal depths may be selected. Changing the pushing beam focal depth will not only alter the magnitudes of induced temperature rises but will also modify the spatial pattern of the induced tissue heating. ARFI-induced tissue heating under varying focal depths and in tissues other than hepatic has been described previously.^{12, 13}

Figure 8 demonstrates that at elevated frame rates, heating of the transducer face can be significant, particularly when conventional ARFI imaging beam sequences are utilized. However, the effects of the transducer face temperature as an additional heat source has been neglected in the FEM thermal models. Alternatively, completely insulating boundary conditions were utilized in the models, such that no heat is allowed to dissipate across the boundary representing the skin-transducer interface. Although neither of these aspects of the thermal model truly reflect actual imaging conditions, they are competing approximations that will largely offset one another in terms of bias introduced into simulation results. The more relevant issue regarding transducer temperature rises is ensuring compliance with IEC standards and safety guidelines during extended periods of ARFI imaging. Although transducer heating would be prohibitive for prolonged high frame rate ARFI imaging sessions, equipment modifications such as actively-cooled or thermally-efficient probes will likely alleviate much of the dependence of ARFI imaging thermal safety on transducer temperatures.

There are several factors associated with elevated tissue temperatures that could potentially impact the quality or consistency of ARFI imaging. For instance, the magnitude of applied radiation force and the elastic modulus of target tissues will be altered by temperature changes. However, these effects will likely only be noticeable in the near field, which is outside the region of interest in abdominal applications. For shallow-depth image applications, the use of a linear transducer is optimal. Temperature-induced changes in sound speed may affect the accuracy of the correlation-based algorithms used to track induced tissue displacements. Since new reference beams are transmitted prior to interrogating each new region of tissue, displacement tracking is only affected by sound speed variations resulting from temperature increases associated with a single pushing beam (∼0.03 °C) and is not impacted by cumulative temperature rises induced by extended imaging sessions. In liver tissues, theoretical displacement errors associated with this temperature increase are roughly 1 μm in magnitude,¹² and occur mainly distal to the focal point (location of peak temperature rise for each pushing beam) at depths usually considered to be outside of the region of interest. Elevated transducer face temperatures may also lead to bulk offsets in tracked tissue displacements. Image artifacts related to transducer face heating can be effectively removed with linear motion filters,²⁸ and do not pose significant concerns for the ARFI imaging method for temperature changes lying within IEC standards.

It should be noted that in vitro thermocouple measurements of ARFI-induced temperature rises in bovine hepatic tissues result in heating magnitudes 25-50% lower than those predicted by models of heating in in vivo human hepatic tissue. The origin of this discrepancy may be due in part to an overestimation of the acoustic intensities transmitted during ARFI imaging. Hydrophone saturation and other measurement complications require in situ ARFI intensities to be estimated using an extrapolation of small-signal derated fields. Conservative scaling factors were implemented at each stage in the extrapolation process. Another cause for this discrepancy is likely due to the fact that the models do not account for power supply variations that are known to occur during the transmission of a pushing pulse. Conservative intensity scaling and ignoring power supply variability likely leads to using higher intensities in the thermal models than are actually achieved in practice. If the experimental (rather than the simulation) results shown in figure 3 were used to generate figures 5 and 6, drastically improved imaging frame rates could be safely employed. Future work will focus on refining the thermal model for greater accuracy, including accounting for nonlinear wave propagation effects, which were neglected by the models in this study. Until these modifications are in place, the conservative models provided in this paper will be used as guides when determining acceptable frame rates.

Recent progress has integrated real-time image visualization with ARFI imaging techniques,^{14, 29} and has accordingly increased the clinical relevance of elevated imaging frame rates. Given the conservative nature of the models in this paper, acceptable frame rates should be limited to those which are not predicted to induce temperature rises greater than 4-5 °C in either tissue or on the transducer face. Using 4-1 parallel receive tracking techniques for an image with a 30 ° FOV, figures 6 and 8 suggest that these frame rates could be as high as 0.4 Hz for imaging hepatic tissue over short (2 min) monitoring windows. If a greater number of parallel tracking channels were available, higher frame rates would likely be safely achievable. Ultimately, conservative decisions governing acceptable ARFI frame rates will need to be made on a case-by-case basis based upon expected target anatomy and imaging conditions. Future efforts will focus on continuing to improve the thermal efficiency of abdominal ARFI imaging.