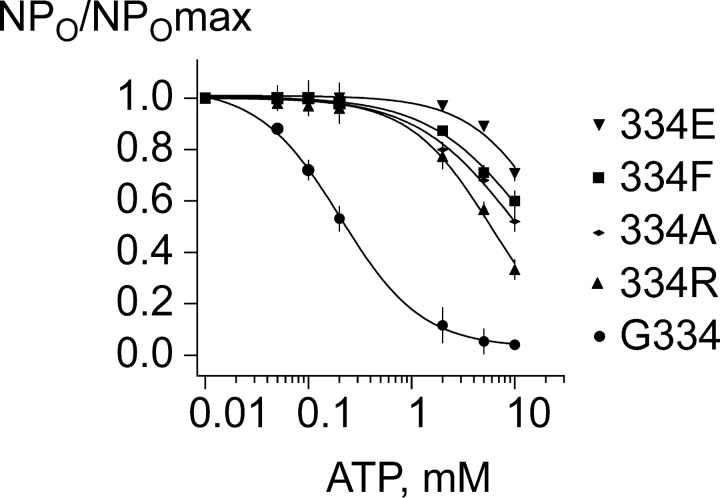
Figure 2.
Dose–response data fit to the Hill equation. To measure the effect of substitutions at position 334 we fit the fractional current as a function of ATP concentration to the Hill equation. The channels show varying changes in the Ki,ATP from 11-fold to over 30-fold, compared with the 0.19 mM value obtained for the wild-type control. The Ki,ATP values for 334 substitutions 334R, 334A, 334F, and 334E were determined in five or more independent experiments and averaged 2.0 ± 0.04, 2.1 ± 0.06, 3.1 ± 0.03, and 5.9 ± 0.02 mM ATP, respectively. Each was significantly increased compared with the parent control values. Although Ki,ATP for the 334R and 334A channels were not significantly different from another, they were each significantly different from the Ki,ATP for the 333F and 334E channels (P < 0.05; one-way ANOVA). In the fits to wild-type Kir6.2ΔC26 channels the slope factor was 1.0 ± 0.1. For the mutant channels, the fits exhibited greater variation in the slope factor, when both the slope factor and Ki,ATP were free parameters. However, previously (Drain et al., 1998; Li et al., 2000) we have found with all wild-type and mutant channels with less mild disruptions in ATP inhibition that the slope factor from fits was 1.0 ± 0.1, as well. We therefore assume that the slope factor does not change by mutations and constrain it to 1.0 ± 0.1 so that we can rank the channels on the basis of the subsequent changes from the fit in the Ki,ATP.