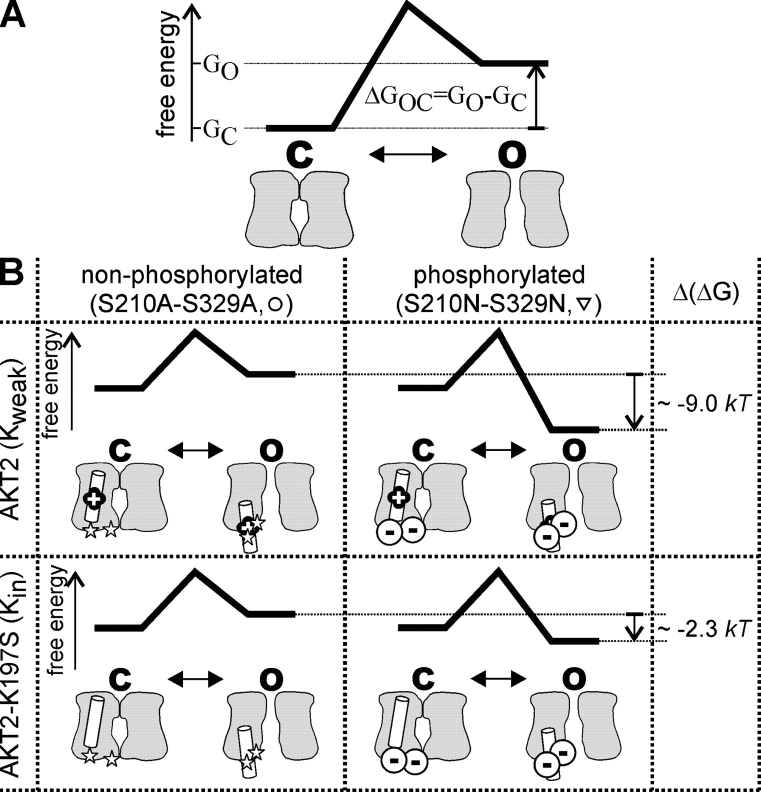
Figure 10.
A model to illustrate the sensitization effect of the lysine residue. (A) A channel can exist in two conformations: open, O, and closed, C. The energy difference between open and closed conformation is ΔGOC = GO − GC. The probability to find the channel in the open conformation calculates as pO = (1 + exp[ΔGOC/(kT)])−1 (Boltzmann function). From the fits to the data in Fig. 9 (G and H), the ΔGOC values for the four channels S210A-S329A, S210N-S329N, K197S-S210A-S329A, and K197S-S210N-S329N are known: ΔGOC S210A-S329A = (0.78 × F/[RT] × [V + 151.9 mV]) × kT, ΔGOC S210N-S329N = (0.78 × F/[RT] × [V − 136.0 mV]) × kT, ΔGOC K197S-S210A-S329A = (1.22 × F/[RT] × [V + 183.1 mV]) × kT, and ΔGOC K197S-S210N-S329N = (1.22 × F/[RT] × [V + 135.5 mV]) × kT. (B) Consideration of four different situations: the channel can be phosphorylated (mimicked by the S210N-S329N mutation) or nonphosphorylated (mimicked by the S210A-S329A mutation), and the S4 region of the channel can contain the lysine residue (AKT2, Kweak, “+”) or not (AKT2-K197S, Kin). The effect of channel phosphorylation, i.e., the energy difference, Δ(ΔG) = ΔGOC P − ΔGOC non-P, between the open conformations of a phosphorylated (mode#2) and a nonphosphorylated (mode#1) channel, can be approximated by calculating the difference in the ΔGOC values between the mutants mimicking the phosphorylated and nonphosphorylated state: Δ(ΔGAKT2) = ΔGOC S210N-S329N − ΔGOC S210A-S329A ≈ −9.0 kT, and Δ(ΔGK197S) = ΔGOC K197S-S210N-S329N − ΔGOC K197S-S210A-S329A ≈ −2.3 kT. It should be noted that the value obtained for the AKT2 wild type is well in line with the energy difference Δ(ΔG) = ΔGOC mode#2 − ΔGOC mode#1 ≈ −8.5 kT obtained from the data in Fig. 6 D.