Isoform switching facilitates period control in the Neurospora crassa circadian clock

Abstract

A striking and defining feature of circadian clocks is the small variation in period over a physiological range of temperatures. This is referred to as temperature compensation, although recent work has suggested that the variation observed is a specific, adaptive control of period. Moreover, given that many biological rate constants have a Q₁₀ of around 2, it is remarkable that such clocks remain rhythmic under significant temperature changes. We introduce a new mathematical model for the Neurospora crassa circadian network incorporating experimental work showing that temperature alters the balance of translation between a short and long form of the FREQUENCY (FRQ) protein. This is used to discuss period control and functionality for the Neurospora system. The model reproduces a broad range of key experimental data on temperature dependence and rhythmicity, both in wild-type and mutant strains. We present a simple mechanism utilising the presence of the FRQ isoforms (isoform switching) by which period control could have evolved, and argue that this regulatory structure may also increase the temperature range where the clock is robustly rhythmic.

Introduction

Circadian rhythms are affected by a variety of environmental stimuli. Of these, light and temperature are the major factors mediating entrainment to daily environmental cycles. For the circadian clock to provide an adaptive advantage, it is important for it to maintain the appropriate phase relationship relative to dawn and dusk such that rhythmic biological processes occur at the optimal time of the day. The responses of the clock must ensure that this phase relationship changes appropriately when the clock is subject to regular perturbations, such as the annual change in day length or temperature, while being resilient to the more or less random perturbations resulting from external environmental fluctuations or due to the stochastic environment of the cell.

Temperature is interesting as an environmental time cue. On the one hand, the clock is sensitive to temperature to the extent that it can act as an entraining factor, but on the other hand, it is insensitive in that the period p of the free-running clock is largely independent of temperature (Gardner and Feldman, 1981; Mattern et al, 1982), with the Q₁₀ of period falling in the range 0.8–1.2. This latter phenomenon, known as temperature compensation, is generally considered to be one of the defining properties of the circadian clock and has been suggested to be a key requirement for stability of the clock's phase relationship to daily environmental cycles, under varying temperatures (Rand et al, 2004). Furthermore, it has been suggested that deviations from perfect compensation—such as the slight undercompensation observed in Neurospora crassa wild-type (WT) strains—contributes to the setting of an appropriate phase under entrained conditions. This implies that the period–temperature profile may be tuned so as to optimise the seasonal adaptation of the clock (Brunner and Diernfellner, 2006; Diernfellner et al, 2007), suggesting that the key requirement for a well-adapted system is a controlled variation in period rather than perfect compensation. Recent research (Liu et al, 1997; Tan et al, 2004; Diernfellner et al, 2005) has also highlighted the question of why circadian clocks oscillate reliably over such a broad range of temperatures, because for some Neurospora mutant strains there are strict limits to the range of temperatures under which the clock is properly rhythmic. Indeed, given that some parameter values are approximately doubling over the temperature range studied, theoretical considerations suggest that loss of rhythmicity is extremely likely.

The Neurospora clock is one of the most comprehensively studied circadian systems (Merrow et al, 2001; Liu et al, 2003). The central components are the rhythmic gene frequency (frq) and the constitutively expressed genes white collar-1 (wc-1) and white collar-2 (wc-2). The protein products of the white collar genes, WC-1 and WC-2, comprise the positive elements of a core negative feedback loop. These form a heterodimeric white collar complex (WCC), which binds to two light-response elements in the frq promoter, activating transcription of frq (Cheng et al, 2001a; Froehlich et al, 2002). When FRQ accumulates beyond a certain level, it interacts with the WCC to inhibit its activation of frq transcription, closing the loop (Cheng et al, 2001a, 2001b; Denault et al, 2001; Merrow et al, 2001; Froehlich et al, 2002). This interaction is mediated by the protein product of an RNA helicase, frh (Cheng et al, 2005). FRQ also positively regulates synthesis of WC-1, forming a positive feedback loop that interlocks with the primary loop (Lee et al, 2000; Cheng et al, 2001a). Here, we discuss the effects of temperature in the context of a new mathematical model for the N. crassa circadian clock. Using this model, we reproduce many of the main features of WT and mutant Neurospora systems, such as their protein profiles, their functional temperature ranges and the dependence of their period upon temperature. We show that although temperature compensation and tuning of the period–temperature profile can be achieved with just one form of FRQ with a temperature-dependent translation profile, the presence of two regulatory loops with opposite temperature dependency controlling the production of two FRQ isoforms greatly simplifies the evolution of such control over the full temperature range, with only a small number of biologically relevant parameters having to be tuned. We also propose that this tuning mechanism—referred to here as isoform switching to reflect its dependence on the switch between the relative abundances of the FRQ forms—naturally increases the functional temperature range of the clock by buffering the system against the loss of robust rhythmicity.

The Neurospora circadian clock

The Neurospora network is particularly interesting from the point of view of temperature regulation because temperature alters the balance of translation between two isoforms of FRQ expressed as a result of alternative initiation of translation from different start codons on the frq open reading frame (ORF). The translation of a longer form (denoted l-FRQ) is initiated at codon 1 while that of a shorter form (denoted s-FRQ) is initiated at codon 100 (Garceau et al, 1997). Furthermore, the rate of FRQ protein synthesis is strongly influenced by temperature. As temperature is raised, short ORFs within the 5′ untranslated region of the frq locus are ignored, resulting in increased translation of the frq ORF (Diernfellner et al, 2005). Consequently, temperature steps cause rapid changes in the level of FRQ, leading to phase shifts (Liu et al, 1998). In addition, more l-FRQ is produced relative to s-FRQ at higher temperatures as a consequence of thermosensitive splicing of intron 6, which removes the initiation codon for l-FRQ (Colot et al, 2005; Diernfellner et al, 2005).

To explore the relationship between this temperature-dependent switch in FRQ isoforms and the dependence of period on temperature, a number of different mutant strains have been developed where effectively only one of the isoforms is present (Liu et al, 1997; Diernfellner et al, 2005). Diernfellner and co-workers constructed mutant strains in which splicing of intron 6 was either constitutive or completely abolished (Diernfellner et al, 2005). When splicing is made constitutive, s-FRQ is synthesised at all temperatures with little l-FRQ produced (this strain will be referred to here as strain A). When splicing is abolished, l-FRQ is efficiently synthesised with only trace amounts of s-FRQ (strain B). Liu et al (1997) constructed similar strains that expressed either s-FRQ alone (strain C) or l-FRQ alone (strain D). Strain D was created by removing the initiation codon for s-FRQ. At low temperatures, a substantial fraction of frq is spliced at intron 6 (Diernfellner et al, 2005), removing the start codon for l-FRQ and therefore preventing its translation. As a result, for strain D there is a substantial reduction in the total amount of FRQ at low temperatures and it becomes arrhythmic (Liu et al, 1997). Strain C was created by introducing a frameshift mutation between the l-FRQ and the s-FRQ AUG. Thus, translation initiation still takes place from the l-FRQ AUG but does not give rise to a functional protein. At high temperatures, almost all frq RNA retains intron 6 and translation is initiated preferentially at the AUG of l-FRQ (Diernfellner et al, 2005). Consequently for strain C, at high temperatures, the amount of FRQ being translated is substantially reduced, and as a result the strain becomes arrhythmic (Liu et al, 1997).

Results

A mathematical model of the Neurospora clock incorporating the two FRQ isoforms

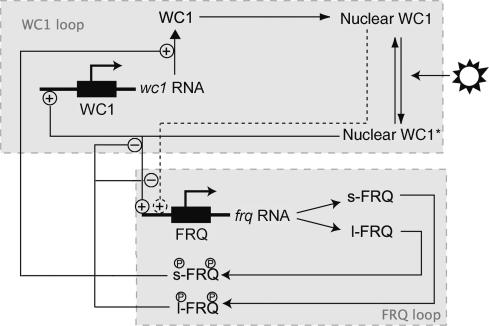
We constructed a model of the Neurospora network incorporating the two genes frq and wc-1 in which the FRQ protein pathway is bifurcated into separate parallel pathways for s-FRQ and l-FRQ. The model is shown schematically in Figure 1. It does not include the genes wc-2 and frh or the light-responsive clock gene vvd, as these factors are not known to function in temperature responses. Care was taken to achieve a good fit to experimental time courses as shown in Figures 5 and 6 of the Supplementary information.

Figure 1.

A schematic representation of the regulatory network underlying the mathematical model of the N. crassa clock. This includes the two genes frq and wc-1 and both the long and short forms of the FRQ protein. WC1^* represents light-activated WC-1.

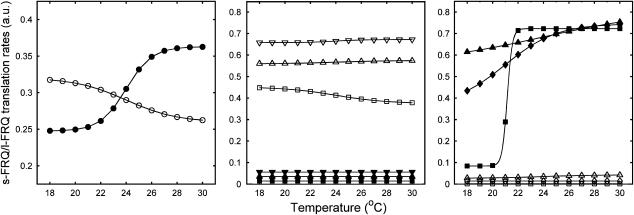
A key ingredient of the model is the shape of the curve chosen for the translation rates of s-FRQ and l-FRQ as a function of temperature. These are different for the WT and the four mutant strains discussed above. The forms used in the model are shown in Figure 2 and further details are given in the Supplementary information (section 4). The simulated FRQ protein profiles generated are in qualitative agreement with experimental data (Liu et al, 1997; Diernfellner et al, 2005).

Figure 2.

Temperature-dependent changes in s-FRQ and l-FRQ translation rates. Open symbols: translation of s-FRQ; closed symbols: translation of I-FRQ. Left panel: WT. Middle panel: mutant strains producing mainly s-FRQ. Inverted triangles: strain A; triangles: strain A with asymmetric FRQ pathways; squares: strain C. Right panel: mutant strains producing mainly l-FRQ. Diamonds: strain B; triangles: strain B with asymmetric FRQ pathways; squares: strain D.

Simulations of temperature dependence and arrhythmicity in WT and mutant strains

Simulated variations of period with temperature for the WT and strains A-D are shown in Figure 3. For the basic near-symmetric model, all parameters of the l-FRQ and s-FRQ pathways except for those controlling translation rates are approximately equal. This reproduced the main features of the WT and strains C and D including the dependence of period upon temperature. However, to reproduce the temperature-dependent increase in period that has been observed experimentally for strain A (Diernfellner et al, 2005, 2007), it was necessary to allow some parameters of the l-FRQ pathway to vary significantly from those of the s-FRQ pathway (see Supplementary information, section 5).

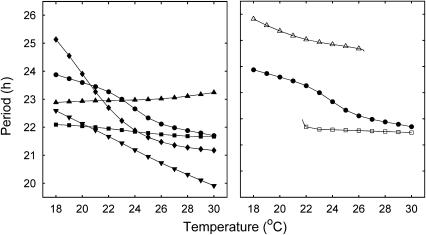
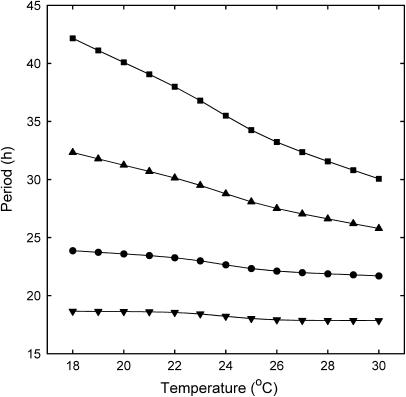
Figure 3.

Dependence of period on temperature for the Neurospora model. Circles denote the WT. Left panel: mutant strains obtained through optimisation or suppression of splicing (Diernfellner et al, 2005, 2007). Inverted triangles: strain A; triangles: strain A with divergent FRQ pathways; diamonds: strain B; squares: strain B with divergent FRQ pathways. For the simulations obtained assuming FRQ pathway asymmetry, strain A has an increasing period–temperature profile, while strain B has a decreasing one with the period of strain A greater than that of strain B, as observed experimentally (Diernfellner et al, 2007). Right panel: mutant strains obtained through modification of the l-FRQ AUG or s-FRQ coding region (Liu et al, 1997). Triangles: strain C; squares: strain D. Strain is compensated at lower temperatures with a period greater than that of the wild-type, becoming arrhythmic at the upper end of the range. Strain D is compensated at higher temperatures with a period smaller than that of the WT, becoming arrhythmic at the lower end of the range. This is in agreement with experimental data (Liu et al, 1997).

Liu et al (1997) reported that expression of either the short or the long form of FRQ significantly reduced the range of temperatures where the clock was rhythmic. The strain expressing l-FRQ alone (strain D) only supports rhythmicity at high temperatures (above 22°C), whereas that expressing s-FRQ alone (strain C) only allows rhythmicity at low temperatures (below 25°C; Liu et al, 1997). The right panel of Figure 3 shows that our model accounts qualitatively for this behaviour, with the simulations of strains C and D becoming arrhythmic close to their experimental values. By contrast, in both the experiments and model, the strains A and B of Diernfellner et al (2005, 2007) maintained rhythmicity across the temperature range even though they effectively only express one form of FRQ.

Brunner and Diernfellner (2006) suggested that the arrhythmicity of strains C and D was due to the reduced overall amount of FRQ protein in these strains. The model supports this explanation and throws some new light on it. Figure 4 shows how total FRQ translation rate varies with temperature in the different strains, resulting in temperature-dependent loss of rhythmicity in strains C and D as total FRQ protein levels fall below critical levels. Insets within Figure 4 show that, as the overall amount of FRQ translation is decreased below a critical value in these strains, the limit cycle shrinks down to an equilibrium with the amplitude of FRQ oscillations converging to zero as this occurs. On the other hand, the model shows that high FRQ protein levels are not necessarily sufficient to ensure clock functionality. If FRQ translation levels are increased too much then the system become arrhythmic again, as excessive FRQ levels turn frq transcription off too quickly (see Figure 4). Thus the optimisation of functionality is not straightforward and FRQ translation rates have to be tuned. It is shown below how this can be achieved and how it is related to temperature compensation and the control of period.

Figure 4.

Simulated changes in total FRQ translation rate with temperature. Filled circles denote the WT. Filled triangles: strain A; filled squares: strain B; open triangles: strain C; open squares: strain D. Thick solid lines denote the net translation rates at which rhythmicity is lost, derived as described in the Supplementary information (section 6). The system is rhythmic for net rates lying between the thick curves, becoming arrhythmic if there is insufficient or excessive translation of FRQ. Inset figures: bifurcation diagrams showing the loss of rhythmicity of strains C and D. For each temperature value on the x-axis, the corresponding value on the y-axis denotes the minimum and maximum levels of FRQ. Solid lines denote stable attractors and broken lines unstable attractors. The solid circles indicate Hopf bifurcations at which the attractor changes from a fixed point (corresponding to arrhythmicity) to a limit cycle (corresponding to rhythmicity).

Characterising period control based on balancing opposite reactions

Hastings and Sweeney (1957) proposed that a balance of opposing reactions could allow temperature compensation (slope of period change with respect to temperature dp/dT approximately 0, denoted dp/dT≈0). This hypothesis was first tested by Ruoff using a simple model for an oscillatory feed-back loop (Ruoff, 1992, 1994; Ruoff et al, 2000). He assumed that the temperature dependence of each of the model parameters k₁,…,k_m was similar to that for rate constants of chemical reactions and was described by the Arrhenius equation. The Arrhenius equation expresses the dependence of the rate constant k_j on the temperature T and activation energy E_j as k_j=A_j exp (−E_j/RT), where A_j is a constant specific to the individual parameter and R is the gas constant (8.314472 J K⁻¹ mol⁻¹). This assumption allowed Ruoff to deduce an expression for the local period slope dp/dT in terms of the activation energies E_j and control coefficients c_j for each of the parameters:

Each term in this expression corresponds to one of the parameters k_j. The product (p/RT²)c_jE_j combines the sensitivity c_j of the period to a change in the parameter k_j with the sensitivity of the parameter k_j to temperature. Because we are using the Arrhenius relation, the latter is (1/RT²)E_j. The control coefficient c_j is defined mathematically by c_j=∂ log p/∂ log k_j, that is, the ratio of the relative change δp/p in period to the relative change in the parameter δk_j/k_j, for a given small change δk_j in k_j with all other parameters fixed.

In our model, the temperature dependence of the s-FRQ and l-FRQ translation rates r_S and r_L are distinct from the other parameters k₁,…,k_m−2, because their dependence on temperature is determined by the thermosensitive post-transcriptional regulation described above and not by the Arrhenius equation. Thus Ruoff's equation is modified to

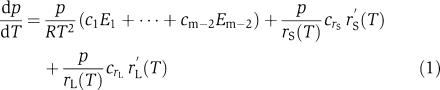(units: h K⁻¹). Here, 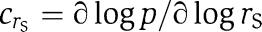and 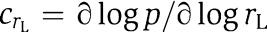are the control coefficients for the parameters r_S and r_L. The quantities r_S′(T) and r_L′(T) are the derivatives of the curves r_S=r_S(T) and r_L=r_L(T), indicating the local change in s-FRQ and l-FRQ translation rates at the temperature T (see Figure 2). For a given model, all the quantities in equation (1) can be easily calculated using the methods of (Rand et al, 2006).

Based on values given in (Ruoff and Rensing, 1996; Ruoff et al, 2005), we expect that a significant proportion of control coefficients will have magnitudes between 0.1 and 1 (cf. Table 6 of the Supplementary information), and that the E_js will be in the region of 1–150 kJ mol⁻¹. The Arrhenius formula predicts activation energies of at least 50 for a parameter k_j with a Q₁₀ of 2 or more, which is the generally accepted value for biological reactions. It follows that a number of the individual terms in equation (1) should each contribute a few hours change in period per degree. For an arbitrary oscillator without any imposed period control mechanism, there is no reason that the positive and negative terms in this sum should balance each other, suggesting that for such an oscillator, we expect a variation of period of several hours over a 10°C temperature range.

To be able to obtain temperature compensation (dp/dT≈0) at a given temperature T=T₀, it is necessary that the more significant terms in equation (1) balance each other out and therefore have different signs. This can be achieved by adjusting either the control coefficients c_j, the activation energies E_j or the FRQ translation rates r_S and r_L. Adjusting the activation energies E_j would be equivalent to altering the components of the oscillator to change binding constants for example, whereas altering the control coefficients c_j (which are functions of the parameters k_j) could be achieved through changes in the activities of regulatory proteins that modulate the rate of post-translational modification or proteolytic degradation of these oscillator components.

One approach to temperature compensation (Ruoff, 1992, 1994; Ruoff et al, 2000) involves balancing equation (1) to get dp/dT≈0 at a single temperature T₀. Such single-point balancing, referred to as ‘static compensation' in (Ruoff et al, 2007), can achieve local compensation even for simple negative feedback loop models. However, the period p as a function of temperature near T₀ will be a parabolic curve of the form p(T)=a+b(T−T₀)²+c(T−T₀)³+d(T−T₀)⁴+…. Formulas for the parameters b, c, d etc can be derived. The formula for b is given in section 4 of the Supplementary information. Using this formula with typical values for the variables it depends on, one sees that b may well be of order 0.1 or more for a system where balance has been achieved by this local method, resulting in significant quadratic variations of the period about the balance point. Thus to ensure good compensation over a significant interval of temperatures, it is necessary that the terms b, c, d etc are made small, meaning that many parameters have to be independently tuned.

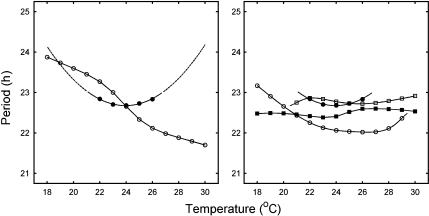
An example of a locally compensated system obtained through the single-point technique is shown in Figure 5, demonstrating the expected parabolic change in period with temperature. Interestingly, the clock becomes arrhythmic as temperature changes away from T₀. Testing of a large number of parameter sets for which our model is locally compensated indicated that this behaviour was typical of such systems (data not shown).

Figure 5.

Left panel: comparison of isoform switching and single-point methods for temperature compensation of WT strains. Open circles: globally compensated system obtained through isoform switching; filled circles: system obtained through single-point (local) compensation at the midpoint of the range assuming identical FRQ pathways the system becomes arrhythmic at the ends of the temperature range; broken line: quadratic curve fitted through the data points. Right panel: simulations of period profile evolution. Filled squares: system obtained by modelling randomised tuning of the locally compensated system to a constant period of 22.5 h through isoform switching (for details, see the Supplementary information, section 8); open squares: partially compensated system observed at an intermediate stage in the tuning process, corresponding to balancing of equation (1) at the upper end of the temperature range; open circles: system obtained through randomised tuning of the locally compensated system assuming identical FRQ pathways.

A novel mechanism for period control based on the balancing of two parallel, temperature-dependent feedback loops

If only one form of FRQ is present, the last two terms in equation (1) are replaced by 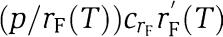where r_F(T) is the total FRQ translation rate and C_TF is the corresponding control coefficient. Setting dp/dT=0 in equation (1) gives

and this can be solved for r_F(T) since (log r_F(T))′=r_F′(T)/r_F(T).

Thus it is possible in principal to obtain global temperature compensation or, more generally, a controlled period change with only one form of FRQ by adjusting the temperature-dependent profile of total FRQ translation r_F(T) appropriately. Indeed, the simulations of strains A–D shown in Figure 3 were obtained by tuning the net translation profile (Supplementary information, section 5). In general, however, such tuning will be a high-dimensional process requiring the adjustment of a large number of independent parameters.

Thus, although our simulations demonstrate that compensation is possible with only one form of FRQ, we argue that the key advantage of having two FRQ isoforms is that it leads to an effective decoupling of the evolution of balance at the upper and lower temperatures, enabling much easier balancing of equation (1). In fact, we show below that tuning of only three parameters is required to obtain a system with a Q₁₀ close to 1, as well as providing sufficient flexibility to exert control over the particular form of the period–temperature profile. The point is that the tuning becomes much more straightforward with the two separate loops than with a single form of FRQ, because in the latter case all the adjustments have to be made simultaneously, because they interact with each other, rather than one at a time.

We make three assumptions in our approach, all based on biological data for Neurospora: (1) at the upper temperature of the physiological range T₂, the abundance of l-FRQ dominates that of s-FRQ; (2) at the lower temperature of the range T₁, the abundance of s-FRQ is either comparable or superior to that of l-FRQ; (3) there is a gradual change in the balance of l-FRQ and s-FRQ abundance at intermediate temperatures. To achieve compensation over the entire range of temperatures, we must achieve three goals, which correspond to three equations: local compensations at both ends of the range (dp/dT=0 at T₁ and T₂) and an appropriate small difference Δp=p(T₂) p(T₁) between the periods at each end of the range. (For WT Neurospora, Δp is negative between 22 and 28°C, corresponding to an undercompensated system (Liu et al, 1997; Diernfellner et al, 2005, 2007).) A key condition is that locally the three equations are independent. This implies not only that three parameters are necessary and sufficient for tuning but also, after some mathematical analysis, that almost any three parameters will suffice. Of course, some parameters will be more effective than others, as we discuss below.

This independence can be readily seen from the following general argument. At the upper temperature T₂, the abundance of l-FRQ protein dominates that of s-FRQ. Thus, at this temperature, the terms in the balance equation (1) corresponding to the l-FRQ pathway dominate the s-FRQ ones. Therefore, if we use only changes in the s-FRQ terms to obtain dp/dT=0 at the lower temperature T₁, these changes will hardly affect the balance at T₂—that is, balancing using s-FRQ terms at the lower temperature and l-FRQ terms at the upper end makes the two operations effectively independent. Tuning of the period difference Δp at the upper and lower temperatures is independent in a similar fashion. In practice, one can directly tune the system by iteratively adjusting the parameters outside of the l-FRQ pathway to get dp/dT=0 at T₁, then adjusting the FRQ translation profiles to get the required Δp, and finally tuning the parameters of the l-FRQ pathway to obtain dp/dT=0 at T₂ (see section 4 of the Supplementary information). This will generally require the adjustment of one parameter for each of these requirements, with that controlling Δp determining the degree of under- (or over-) compensation.

To demonstrate the robustness of this mechanism and to show that it facilitates evolutionary tuning, after tuning the system we have perturbed it away from the tuned state by randomly changing the parameters and then used a stochastic annealing process to retune it. This involved randomly changing the activation energies E_j and FRQ translation profiles r_S(T) and r_L(T) of the model so as to minimise a cost function measuring the difference between the detuned system and a compensated one. (A similar cost function was employed by Ruoff (1994) to quantify the degree of temperature compensation in solutions of a Brusselator model.) As a result, we produce a new tuned system distinct from the original one (i.e., with different parameter values). This perturbation and retuning process, which is detailed in section 8 of the Supplementary information, can be repeated ad infinitum. Although it is not meant to model any true evolutionary process, its robust success in repeatedly retuning the system demonstrates the ease with which such stochastic processes can achieve the compensated states and suggests that they may be similarly robustly obtained by the small incremental changes typical of natural evolutionary processes. Moreover, we have started this annealing process from systems that were not well compensated and/or had a limited temperature range of rhythmicity and seen that the resulting system is not only compensated but also has a broader functional range (see Figure 5; see also Figure 9 of the Supplementary information). In addition, comparisons of the annealed period profiles obtained with and without isoform switching confirmed the increased flexibility in period control conferred by the parallel FRQ pathway architecture (see Figure 5).

Identification of the parameters contributing to period control in the Neurospora clock

We have used the techniques of Rand et al (2006) to examine which aspects of the system provide the most effective parameters for tuning. These are the parameters for which the magnitude of the control coefficient c_j is largest, as these correspond to the dominant terms in equation (1) for dp/dT. We give all the c_j values for our model in Tables 6 and 7 of the Supplementary information. Here we note that the parameters associated with the highest control coefficients are the translation rates for s-FRQ and l-FRQ, the mean delay τ for FRQ transcription factor conversion and the maximal degradation rate for frq mRNA. The delay τ is an important parameter of our model. In vivo, the FRQ protein is known to exhibit post-translational regulation through multiple phosphorylation events, interaction with protein partners and changes in cellular localisation. In the model, τ is the mean time for a protein molecule to undergo these processes and become an active transcription factor. Consequently, changes in parameters affecting one or more of these process can be quantified in terms of changes in τ. For example, if the major contributor to the delays in the FRQ feedback loops was phosphorylation events, τ would be inversely proportional to the net phosphorylation rate.

The other important parameters in terms of their control coefficients are the frq transcription rate, the strength of the negative regulation of frq transcription by FRQ transcription factor and the degradation rate of intermediate FRQ species. All other parameters have control coefficients c_j that are significantly smaller. Table 8 of the Supplementary information shows the predicted changes to the period Q₁₀ resulting from perturbations to the parameters with high c_js. The simulations suggest that changing the delay τ in the s- and l-FRQ loops will have opposite effects on the period profile, with increases in the s-FRQ delay leading to an increased Q₁₀ and increases in the l-FRQ delay yielding a reduced Q₁₀, with a sufficiently large l-FRQ delay leading to a positive gradient (Q₁₀<1).

Ruoff et al (2005) showed that altered rates of bulk FRQ protein degradation (described here as r) for different frq mutant alleles could account for defective temperature compensation. However, each of the different states of FRQ produced by the processes mentioned above may exhibit a different rate of degradation. The rate of bulk FRQ degradation therefore depends on a nonlinear combination of these rates together with the rates of protein modification and transport (see section 9 of the Supplementary information). Thus, in our detailed model, r depends both on the degradation of cytoplasmic and nuclear FRQ and on the mean delay τ (as quantified in the Supplementary information). Indeed, changes in τ result in significant changes in r, and therefore the dependence of dp/dT on τ is consistent with the dependence upon r in Ruoff's simple model (Ruoff et al, 2005). It is in fact possible to manipulate τ so as to simulate the compensation mutants associated with changes in FRQ stability reported in (Ruoff et al, 2005). Figure 6 shows simulations of several of these mutants obtained by appropriate adjustments to τ. However, the higher level of detail of our model allows us to narrow down aspects of regulation that contribute to period control, highlighting the greater contribution of FRQ protein modification and/or nuclear translocation as compared with FRQ protein degradation (for further details, see section 9 of the Supplementary information).

Figure 6.

Simulated period–temperature profiles of compensation mutants associated with changes in FRQ stability (Ruoff et al, 2005). Circles: WT; inverted triangles: frq¹; triangles: frq⁷; squares: frq^S5131. frq¹ is compensated with a smaller period than WT. frq⁷ and the Ser513 phosphorylation site mutant frq^S5131 have larger periods than WT and significant negative period–temperature slopes across the range, with the period of frq^S5131 greater than that of frq⁷. These profiles and the corresponding relative net FRQ loss rates (Supplementary Table 11) are in qualitative agreement with experimental data (Ruoff et al, 2005).

Using temperature dependence to probe molecular mechanisms

If it is assumed that the l-FRQ and s-FRQ pathways are symmetric—in that they undergo nearly identical molecular processes and are functionally equivalent—then it can be shown that the slope of the curve p(T) describing the change in period as a function of temperature will be roughly equal for the WT and for strains A–D (Supplementary information, section 5). Thus if period decreases with temperature in the WT, then so should that of the mutant strains. However, there is experimental evidence that for the s-FRQ only mutant produced through the modification of thermosensitive splicing (strain A), period increases with temperature (Diernfellner et al, 2005, 2007). This suggests that the symmetry in the s-FRQ and l-FRQ pathways is broken, raising the question of which aspects of the pathways may be divergent. As our results suggest that the temperature-dependent change in period p(T) is most sensitive to the modification and transport processes affecting the two FRQ forms, it follows that either some of these processes have different rate constants or that the two forms of FRQ have different effectiveness as transcription factors. It is unclear which process is affected in this case.

Implications for the high and low temperature limits of clock functionality

Our results suggest that, in addition to facilitating period control, the parallel loop structure of the Neurospora circadian clock increases the range of temperatures where the clock functions. This can be understood by considering the behaviour of our model when periodicity breaks down. Hopf bifurcations are one of the two typical ways in which periodic oscillations can be destroyed as a variable such as temperature T is altered. For the Hopf bifurcation, as T increases past a certain critical value T_H, oscillations can either grow continuously from an equilibrium point or alternatively collapse to it in a mirror image with the amplitude of the oscillations proportional to 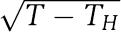. Our model predicts such behaviour for strains C and D (see Figure 4), and this result is consistent with experimentally observed, temperature-dependent changes in the amplitude of their conidiation rhythms (Liu et al, 1997).

Any loss of rhythmicity through a Hopf bifurcation as temperature is varied will be accompanied by convergence of the period p(T) of the oscillatory solution to the period p_e associated with the corresponding unstable equilibrium. Consequently, if p(T) is kept roughly constant and therefore bounded away from p_e within a given temperature interval, then the system is less likely to approach a Hopf bifurcation in this range. Thus, compensation of the clock can also result in improved functionality by buffering the system against temperature-dependent reductions in the amplitude of the rhythms or the loss of self-sustained rhythmicity altogether. The parallel loop structure of the Neurospora network means that compensation—and thus robust rhythmicity—can be obtained independently at the upper and lower ends of the temperature range, providing a simple mechanism for extending the functionality of the clock across the whole physiological range. By contrast, single-point compensation at an intermediate temperature will guarantee robust rhythmicity about the balance point but not at the temperature extremes (see Figure 5). Viewed in terms of net FRQ translation, the parallel loop structure provides a means of independently adjusting the translation rates at the end points, making it easier to obtain a translation–temperature profile that stays within the rhythmicity boundaries (see Figure 4).

Discussion

A generic mechanism for period control?

The evolution of a molecular mechanism to provide a relatively complex modulation of the translation rates of two different forms of the same protein is a fascinating example of how much circadian clocks can diverge from the simple delayed negative feedback loop that will reliably oscillate. Our contention is that this mechanism is there to aid the balance of equation (1), providing a simple means of ensuring that (i) the period temperature profile is controlled; and (ii) the clock remains functional over a broad range of temperatures. We also contend that these two aims are related and that any mechanism to produce one is likely to affect the other. To demonstrate that the mechanisms discussed apply broadly, a simple model adapted from that of Leloup and Goldbeter (1999) has also been discussed in the Supplementary information. We also propose that although the mechanisms discussed here are based on current experimental information about the Neurospora clock, much can be readily abstracted to a general mechanism that can be adapted to many other systems exhibiting a temperature-dependent switch in the levels of two or more key isoforms. Although molecularly different, the ways in which other systems achieve compensation and/or robustness may be mathematically similar. A possible candidate is the temperature-dependent splicing of per mRNA in Drosophila (Majercak et al, 1999). The ratio of the spliced to the unspliced variant is higher at low temperatures, and it is argued that this information concerning ambient temperature is involved in optimally aligning activity rhythms to environmental conditions (Majercak et al, 1999).

Temperature regulation of period in the Neurospora clock

Conidiation rhythms in WT Neurospora exhibit good temperature compensation, yet period decreases slightly with rising temperatures i.e. the WT is slightly undercompensated. In contrast, strains C and D, which were engineered to express a single form of FRQ, exhibit a nearly constant period over their functional temperature range (Liu et al, 1997). Our model enables us to quantify this difference between the WT and strains C and D in terms of the relationship between net FRQ translation and the period–temperature profile of the Neurospora clock. In our model and others (Ruoff et al, 2005), the control coefficients describing the effects of changes in FRQ translation rate on period are significant. Consequently, if the temperature profile of FRQ translation is altered, this will affect how period varies with temperature (cf. equation (1)). At the lower end of the temperature range, strain C is slightly undercompensated, with a similar period slope to the WT. This is because the total FRQ translation rates of these strains have similar values and slopes at the lower end of the temperature range (see Supplementary information, section 5). However, as temperature increases, strain C exhibits a shallower translation slope compared with the WT with a correspondingly smaller slope in period. At the upper end of the range, the total amount of FRQ protein is significantly decreased and strain C stops oscillating. On the other hand, strain D is almost perfectly compensated and the change in slope of p(T) between strain D and the WT is accounted for by the change in the slope of the total FRQ translation rate, as can be seen in Figure 4. Again, the loss of rhythmicity in strain D at the lower end of the temperature range is a consequence of a significant reduction in the total amount of FRQ.

The small period–temperature slopes observed experimentally in strains A and B demonstrate that good compensation can be achieved with a single form of FRQ (Diernfellner et al, 2005, 2007). Our simulations are consistent with this finding, and further show that the period–temperature profile can be tuned through appropriate adjustment of the net FRQ translation profile. In general, however, such tuning will involve the adjustment of a large number of parameters. This suggests that in Neurospora, temperature compensation may be achieved by a mechanism independent of FRQ isoform switching. Alternatively, the good compensation observed in the single FRQ isoform strains could be a consequence of the fact that—as discussed at the end of the Results section—small period gradients are likely to be observed in any system that is robustly rhythmic over a given temperature range, as loss of rhythmicity will generally be accompanied by significant period changes within the range.

In either case, our contention is that the presence of two isoforms of FRQ and a thermosensitive switch in their ratio greatly simplifies the balancing of equation (1) across the full temperature range, while also conferring control over the global form of the period profile. Indeed, we show that global period control can be achieved through the alteration of only three parameters. Two of these parameters are adjusted so as to obtain locally compensated systems at the extremes of the temperature range, whereas the third parameter adjusts the difference between the periods at the ends of the range, enabling the overall slope of the period temperature profile to be tuned. The small number of parameters to be adjusted suggests a relatively simple mechanism by which perfect compensation—or a controlled change in period with temperature—could arise through natural evolution for any biological oscillator having a similar parallel pathway structure.

Relating the control of period to the control of entrainment phase

The exact value of the free-running period in constant conditions does not appear to have a direct selective value in the natural environment, as the clock will normally be entrained to diurnal day/night cycles. One may therefore ask why temperature compensation has arisen during evolution. A possible explanation is that the preservation of the free-running period p(T) under temperature changes is a secondary phenomenon, resulting from the necessity for robust entrainment together with the maintenance of appropriate phases of rhythmic processes across the physiological range of temperatures. This would presumably have a selective advantage (Yan et al, 1998; Dodd et al, 2005). As is well known, the phase of a forced oscillator depends strongly on the ratio of the free-running period p to the forcing frequency (Rand et al, 2006). Thus, some degree of period control will be necessary for robust phase entrainment. However, it may well be the case that to optimise the phases with respect to temperature changes, it is necessary to have some change in period with temperature (Brunner and Diernfellner, 2006; Diernfellner et al, 2007).

In the Supplementary information (section 7), we confirm that control of the period profile p(T) gives control of phase as a function of temperature. For the simulated WT, the phase of entrainment—taken as the onset of conidiation (Merrow et al, 2006)—occurs roughly in the middle of the night independent of temperature. By contrast, phase is delayed compared with WT in the s-FRQ only strain A and advanced in the l-FRQ only strain B, reflecting the differences in the corresponding profiles (see Figure 8 of the Supplementary information). The flexibility to tune the period difference Δp across the temperature range conferred by the loops associated with the FRQ isoforms provides a simple means of achieving a controlled change in period and thus phase across the desired temperature range.

Biological implications

The modelling identifies a number of key parameters whose alteration is most likely to affect compensation and the functional temperature range of the clock. In addition to the s-FRQ and l-FRQ translation rates, these include the mean delay τ for a newly translated FRQ protein to feedback on its own transcription, the frq transcription rate, the maximal degradation rate of frq mRNA and the strength of the negative regulation of frq transcription by FRQ protein. Indeed, our model identifies the delay τ as the parameter most likely to be affected in compensation mutants arising from modification of the net FRQ degradation rate (Ruoff et al, 2005). This implicates processes affecting FRQ modification or nuclear translocation as the key factors responsible for these phenotypes, rather than the degradation rates of different FRQ proteins. Experimental manipulation of any of the key rates listed above could be used to disrupt temperature compensation. It should then be possible to manipulate another of these rates so as to obtain a new compensated clock with different parameters.

We have pointed out that the overcompensation observed in strain A suggests the existence of an asymmetry between the two FRQ forms. This could be a consequence of s-FRQ and l-FRQ undergoing modification or transport processes with significantly different rate constants or from the forms being functionally distinct. These possibilities could be investigated experimentally by, for example, testing whether the isoforms exhibit differential phosphorylation or have different efficacy as suppressors of frq production. Our modelling also suggests that manipulation of the feedback delays in the FRQ loops will have opposite effects on the period Q₁₀, with a greater mean s-FRQ transcription factor conversion time yielding an increased Q₁₀ and a greater mean l-FRQ TF conversion time resulting in a smaller Q₁₀. This prediction is also amenable to experimental testing, through, for example differentially changing the s-FRQ and l-FRQ phosphorylation rates and observing the subsequent effects on the Q₁₀.

Finally, our results suggest that a noncompensated clock is likely to exhibit reduced functionality, because at some critical temperature T_H within or close to the physiological temperature range there will be a Hopf bifurcation, leading to damped or low-amplitude oscillations rather than robust, self-sustained rhythms. In this case, we predict that the amplitude of the oscillations should decrease proportionally to 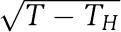as the temperature T approaches T_H (cf. the insets to Figure 4). A distinct experimental signature where the rhythm freezes at a well-defined phase without changing amplitude as T approaches T_H would indicate a different type of widely observed bifurcation, where at the critical temperature an equilibrium point is born on the limit cycle (Guckenheimer and Holmes, 1983). Such an observation would be incompatible with our model in its current form.

Conclusions

Maintaining self-sustained rhythmicity over a wide temperature range will confer a selective advantage, because a self-sustained oscillator is more likely to be able to be robustly entrained and to be robust to stochastic perturbations than one displaying damped oscillations. Thus, compensation may have been initially selected for during evolution as a consequence of the need to maintain the clock's ability to oscillate over a broad range of temperatures. Subsequently, the advantage conferred by having an entrainment phase robust with respect to seasonal variations in temperature could have led to the particular, tuned period–temperature profiles observed experimentally. In Neurospora, the thermosensitive switch in the s-FRQ:1-FRQ ratio comprises a simple low-dimensional mechanism that may underlie the development of temperature compensation and, more broadly, the buffering of entrainment phase against temperature fluctuations.

Materials and methods

Modelling

The viability of isoform switching as a mechanism for period control was initially assessed by applying it to a simple model of the Neurospora network involving only the frq gene. This consisted of five ordinary differential equations based on the network used in (Leloup and Goldbeter, 1999) and is referred to as model 1 in the Supplementary information. The more realistic model discussed here comprised a set of 6 integrodifferential equations describing the dynamics of the frq and wc-1 genes. It is described in detail in section 2 of the Supplementary information where it is referred to throughout as model 2.

Computational methods

Solutions of the primary model consistent with experimental data were obtained by using a technique developed for fitting noisy, poorly sampled time series (Locke et al, 2005). This method used a cost function based on reproducible, qualitative features of experimental time courses, such as the period of the oscillations and the phases at which the different components of the clock attained their peak values (Locke et al, 2005). A low cost (indicating a good fit to the data) was obtained for parameter sets that allowed the model to be entrained to LD 12:12 cycles, with a DD solution that had a period close to 22 h for which FRQ peaked approximately 4–6 h after its transcript and oscillated roughly in antiphase with WC-1 (for further details, see section 3 of the Supplementary information).

Direct computation of the period derivatives for these low-cost solutions through the limit cycle perturbation technique described in Rand et al (2006) enabled equation (1) to be directly balanced using isoform switching so as to obtain simulations of WT temperature data. This balancing method is outlined fully in section 4 of the Supplementary information, while sections 5 and 9 describe the modifications to the WT solutions required to simulate the single FRQ form mutant strains A–D and the mutants associated with changes in FRQ stability. The translation-rate-dependent bifurcation boundaries plotted in Figure 4 were computed by considering families of models interpolating between rhythmic and arrhythmic systems, parameterised implicitly by the net FRQ translation rate (for further details, see section 6 of the Supplementary information).

All numerical routines for model simulation and analysis—including bifurcation codes—were implemented with custom software written in MATLAB (Mathworks, Cambridge). Cost function optimisation was implemented by compiling MATLAB code into C and running the code on a task farm computer consisting of 62 × 2.6 GHz Xeon CPUs. The software for analytical computation of period derivatives is available for download from http://millar.bio.ed.ac.uk/PEBrown/IRCs.htm. MATLAB versions of the model together with all parameter sets used in the simulations shown are available by request from oakman@staffmail.ed.ac.uk.

Supplementary Material

Supplementary Information

Supplementary Information

Supplementary Information