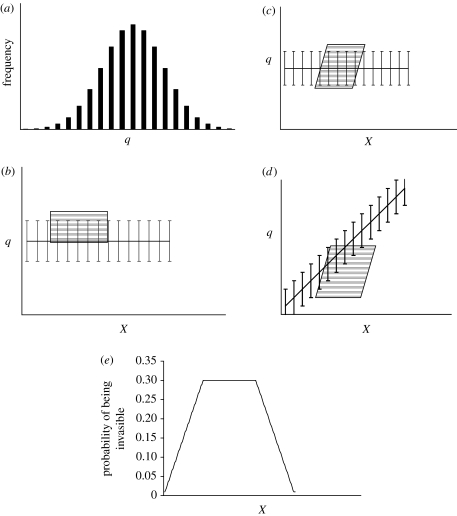
Figure 1.

Conceptual model: the effect of an unknown factor (q) on the relation between a known variable (X) and invasibility. (a) A hypothetical normal frequency distribution for the unknown factor is shown for illustration, but other frequency distributions are possible. The overlap of the frequency distribution of the unknown variable and the environmental conditions that are invasible (the shaded boxes) determines the proportion of sites that are invasible. This is shown for: (b) no interaction (rectangular box) and no correlation (horizontal line) between unknown (q) and known (X) variables; (c) interactions present between q and X in determining invasibility (i.e. the permissible values of X where survival is possible change with q) and (d) interaction and correlation (i.e. non-horizontal line indicating that the distribution of q values changes across X) exist. (e) A hypothetical probability distribution for invasibility based on a measured variable. Since we have only measured X, but invasibility is dependent on X and q, if interactions and/or correlations exist, the degree of overlap of the unknown q distribution should change over X, resulting in a probability distribution for invasibility. The actual shape of the probability distribution will depend upon shape of the interactions and correlations, and will have as many dimensions as there are known environmental variables.