Compartmental models of rat cerebellar Purkinje cells based on simultaneous somatic and dendritic patch-clamp recordings

Abstract

1. Simultaneous dendritic and somatic patch-clamp recordings were made from Purkinje cells in cerebellar slices from 12- to 21-day-old rats. Voltage responses to current impulses injected via either the dendritic or the somatic pipette were obtained in the presence of the selective I_h blocker ZD 7288 and blockers of spontaneous synaptic input. Neurons were filled with biocytin for subsequent morphological reconstruction.

2. Four neurons were reconstructed and converted into detailed compartmental models. The specific membrane capacitance (C_m), specific membrane resistance (R_m) and intracellular resistivity (R_i) were optimized by direct fitting of the model responses to the electrophysiological data from the same cell. Mean values were: C_m, 0.77 ± 0.17 μF cm⁻² (mean ±s.d.; range, 0.64-1.00 μF cm⁻²), R_m, 122 ± 18 kΩ cm² (98-141 kΩ cm²) and R_i, 115 ± 20 Ω cm (93-142 Ω cm).

3. The steady-state electrotonic architecture of these cells was compact under the experimental conditions used. However, somatic voltage-clamp recordings of parallel fibre and climbing fibre synaptic currents were substantially filtered and attenuated.

4. The detailed models were compared with a two-compartment model of Purkinje cells. The range of synaptic current kinetics that can be faithfully recorded using somatic voltage clamp is predicted fairly well by the two-compartment model, even though some of its underlying assumptions are violated.

5. A model of I_h was constructed based on voltage-clamp data, and inserted into the passive compartmental models. Somatic EPSP amplitude was substantially attenuated compared to the amplitude of dendritic EPSPs at their site of generation. However, synaptic efficacy of the same quantal synaptic conductance, as measured by the somatic EPSP amplitude, was only weakly dependent on synaptic location on spiny branchlets.

6. The passive electrotonic structure of Purkinje cells is unusual in that the steady-state architecture is very compact, while voltage transients such as synaptic potentials and action potentials are heavily filtered.

Although great progress has been made in our understanding of the active properties of neuronal dendrites in recent years (reviewed by Häusser et al. 2000), controversy and uncertainty remain about the passive membrane properties of neurons. This debate is still relevant since the passive membrane properties largely determine the propagation and summation of synaptic potentials (Rall, 1964; Spruston et al. 1994), and must also be taken into account when performing voltage-clamp studies of synaptic currents. Furthermore, the activation of dendritic voltage-gated currents and the resulting dendritic electrogenesis, which can affect neuronal output patterns, rely crucially on the properties of the passive electrotonic ‘skeleton’ (Pinsky & Rinzel, 1994; Mainen & Sejnowski, 1996; Vetter et al. 2001). Determining the passive membrane properties of neurons and constructing accurate passive compartmental models therefore continues to be of central importance to our understanding of neuronal function.

The representation of the electrotonic structure of the neuron as a series of compartments, each with an intracellular resistivity (R_i), specific membrane resistance (R_m) and specific membrane capacitance (C_m), originates from the work of Rall (1964). More recent compartmental models have combined electrophysiological and morphological data from the same cell (Redman & Walmsley, 1983; Clements & Redman, 1989; Major et al. 1994; Rapp et al. 1994; Chitwood et al. 1999) or from the same cell type (Johnston & Brown, 1983; Shelton, 1985; Spruston & Johnston, 1992; Mainen et al. 1996) to provide more reliable estimates of the model parameters. While these models have proved extremely useful, many of them suffer from serious non-uniqueness in the model parameters; that is, there exist a variety of combinations of parameters which provide equally good fits to the available data (Stratford et al. 1989; Major et al. 1993).

The great majority of previous passive modelling studies have gathered electrophysiological data from somatic recordings only, and one potential solution to the problem of non-uniqueness in the model parameters is to record simultaneously from two points on the same neuron (Stuart & Spruston, 1998). This configuration has several important advantages. First, it provides data from two distinct locations on the same cell, increasing the amount of information against which the model must be constrained. Second, the attenuation of signals between one recording site and the next is highly sensitive to the electrotonic structure, particularly the intracellular resistivity (Major, 1993). Third, reciprocity relations between the two current injection sites can provide an important test of the linear behaviour of the neuron (Major et al. 1993; Ulrich & Stricker, 2000; Berger et al. 2001). Fourth, recording from multiple sites can provide information about non-uniformities in the membrane properties (Stuart & Spruston, 1998; Berger et al. 2001). Finally, since one electrode records signals while the other injects current, at least at one recording site the entire waveform is largely unaffected by pipette artifacts related to current injection, which can seriously compromise estimation of R_i (Major et al. 1994).

Here we use the patch-clamp technique to make simultaneous recordings from two sites on the same Purkinje cell (Stuart & Häusser, 1994; Häusser & Clark, 1997), with one pipette located at the soma and another pipette located on a dendrite. This offers the additional advantage that the shunt associated with microelectrode recording can be neglected due to the high (gigaohm) resistance of the patch-clamp seal (Major et al. 1994). We construct compartmental models based on complete morphological reconstructions of the cells recorded from, and determine their electrical parameters by direct fitting of dendritic and somatic impulse responses. To assess the reliability of the models we use resampling techniques (Efron & Tibshirani, 1993) to estimate statistical and systematic errors in the best-fit model parameters. The error analysis demonstrates that predictions of the models, such as the attenuation of EPSCs or EPSPs from their dendritic origin to the soma, may be more robust than suggested by the uncertainties in individual electrical and morphological parameters, which trade off against each other. We also test the assumptions and predictions of a reduced two-compartment model of Purkinje cells (Llano et al. 1991) by comparing it with our detailed multicompartmental models. Preliminary results from this study have been presented in abstract form (Roth & Häusser, 1999).

METHODS

Experiments

Electrophysiology

Simultaneous whole-cell patch-clamp recordings were made from the dendrites and somata of visually identified Purkinje cells in rat cerebellar slices as previously described (Stuart et al. 1993; Stuart & Häusser, 1994). Wistar rats aged 12-21 days postnatal (P12-21) were killed by decapitation in accordance with local regulations and sagittal slices (250-300 μm) were cut on a vibratome (Dosaka, Kyoto, Japan) in ice-cold extracellular solution containing (mm): 125 NaCl, 2.5 KCl, 25 glucose, 25 NaHCO₃, 1.25 NaH₂PO₄, 2 CaCl₂ and 1 MgCl₂. The slices were incubated at 34 °C for 45 min and then kept at room temperature before transfer to the recording chamber. Purkinje cells were viewed using an upright microscope (Axioskop FS, Zeiss, Göttingen, Germany; × 60, 0.9 NA water-immersion objective, Olympus, Tokyo, Japan) and infrared differential interference contrast (IR-DIC) videomicroscopy (Stuart et al. 1993). Experiments were carried out at room temperature (23 ± 1 °C).

Recordings in current-clamp mode were made using two Axoclamp 2B amplifiers (Axon Instruments, Foster City, CA, USA). Pipettes (5-7 MΩ) were coated with Sylgard 184 (Dow Corning, Midland, MI, USA) to reduce their capacitance. The internal patch-pipette solution contained (mm): 100 potassium gluconate, 20 KCl, 10 Hepes, 10 EGTA, 4 Na₂ATP, 4 MgCl₂ and 0.5 % biocytin (295 mosmol kg⁻¹; pH adjusted to 7.3 with KOH). The external solutions contained 30-50 μm ZD 7288 (Tocris Cookson, Bristol, UK) to block the hyperpolarization-activated cation current (I_h) (Harris & Constanti, 1995). Spontaneous synaptic activity was blocked using 10 μm CNQX, 50 μm picrotoxin and 30 μm SR 95531. Seal resistances before break-in were > 5 GΩ. To generate impulse responses, brief (0.5 ms) positive and negative current pulses (0.5-1 nA) were injected via either the somatic or dendritic pipette at 1.017 Hz. Somatic and dendritic impulses, and impulses of different polarity, were interleaved. Bridge balance was monitored continuously (series resistance was 7-15 MΩ at the somatic pipette and 15-50 MΩ at the dendritic pipette) and optimal capacitance compensation was employed. Voltages were filtered at a bandwidth of 5 kHz (-3 dB) using an 8-pole low-pass Bessel filter and sampled at 20 kHz using pCLAMP software (Axon Instruments). The calibration of the stimulation and recording apparatus was verified using artificial neurons consisting of networks of resistors and capacitors in conjunction with computer models of these neurons.

Somatic voltage-clamp recordings were made from P12-14 Purkinje cells using an Axopatch 200B amplifier (Axon Instruments). The same internal solution was used as for the current-clamp recordings. In order to isolate the hyperpolarization-activated current, I_h, the external solution contained 1 μm TTX, 0.1 mm CdCl₂, 1 mm 4-aminopyridine, 5 mm TEA, 5 μm CNQX and 30 μm SR 95531, and lacked ZD 7288. Series resistances were 5-8 MΩ before compensation, and were compensated by 80-90 %. I_h was activated by 5 s voltage-clamp steps to different test potentials from a holding potential of -50 mV. Deactivation and the reversal potential of I_h were measured by holding at -110 mV for 5 s and then jumping to different test potentials. Membrane potentials were not corrected for the liquid junction potential. All drugs were from Sigma unless otherwise indicated.

Electrophysiological data were analysed using macros in IGOR Pro (Wavemetrics, Lake Oswego, OR, USA), and the program Synaptix (kindly provided by Boris Barbour). During analysis of impulse responses, each sweep was inspected, and sweeps containing significant noise artifacts were rejected. Data are given as means ±s.d.

Histology

At the end of the recording period (< 30 min), pipettes were withdrawn from the cell to form outside-out patches in order to preserve the integrity of the membrane and confirm the integrity of the gigaohm seal. Slices were fixed for 24 h in cold 100 mm phosphate-buffered saline (PBS, pH 7.4) containing 4 % paraformaldehyde. Fixed slices were not dehydrated or resliced in order to minimize tissue shrinkage and/or distortion. After fixation, slices were rinsed several times in PBS and endogenous peroxidases were blocked by incubation of slices for < 10 min in solution containing 1 % H₂O₂, and 10 % methanol in PBS. After washing in PBS, sections were incubated for 2 h in avidin-biotinylated horseradish peroxidase (ABC-Elite, Vector Labs, Peterborough, UK). Following incubation, sections were washed several times in PBS, briefly incubated in a solution containing 0.015 % diaminobenzidine, and developed under visual control using a brightfield microscope until all processes of the cells were clearly visible (usually after 2-4 min). The reaction was stopped by transferring the sections into cold PBS, and slices were mounted in Mowiol (Clariant, Sulzbach, Germany).

Morphological reconstruction

The mounted neurons were digitally reconstructed using a × 100, 1.4 NA oil-immersion objective on a Zeiss Axioplan microscope and Neurolucida software (MicroBrightField, Colchester, VT, USA), which records the visually determined diameters and three-dimensional coordinates of all neurites. To assess possible distortion caused by histological processing (Jaeger, 2001), the diameters and lengths of several dendritic sections measured during the experiment were compared with the same values measured from the fixed neuron; errors were less than 5 % in all cases, and therefore no shrinkage correction was applied to the reconstructed morphology. The position of the dendritic recording site with respect to major branch points was determined visually during the experiment and implemented accordingly in the reconstruction. Possible errors in dendritic diameters and lengths, as well as the position of the dendritic recording pipette, were considered in the analysis of systematic errors in the model (see below).

Theory

Compartmental modelling

All modelling was carried out using NEURON 3.2.3 and 4.1.1 (Hines & Carnevale, 1997, 2000) running on Sun Sparcstations (Sun Microsystems, Palo Alto, CA, USA) and an SGI Origin 2000 server (Silicon Graphics, Mountain View, CA, USA). Reconstructions were converted from Neurolucida to NEURON format using a program written in C. Dendritic and axonal sections were subdivided into compartments (‘segments’) whose length limit was scaled proportional to the square root of the local diameter; the maximum compartment length was 8.3 μm. The number of compartments was increased in dendritic sections adjacent to the somatic and dendritic recording sites. Somata were assumed to be rotationally symmetric and represented by 10 compartments. The total number of compartments was 1190, 1084, 1463 and 2758 for Cell 1 to Cell 4, respectively (see Table 2). Membrane parameters C_m, R_m and R_i were assumed to be uniform across each cell, unless specified differently. The integration time step for all simulations was 10 μs.

Table 2.

Morphological characterization

	Cell 1	Cell 2	Cell 3	Cell 4
Total surface area (without spines; μm2)	15 786	11 788	25 768	40 821
Cell volume (without spines; μm3)	8085	6157	13 161	20 084
Soma
Soma major axis (μm)	25.7	24.5	27.8	29.3
Soma minor axis (μm)	15.9	15.4	17.6	21.7
Soma perimeter (μm)	66.1	64.6	69.8	78.8
Soma surface area (μm2)	1041	938	1240	1635
Dendrites
Maximum width of dendritic tree (μm)	176	138	131	193
Maximum height of dendritic tree (μm)*	122	137	154	210
Total number of dendritic compartments	1151	1064	1168	2455
Number of dendritic branch points	306	273	348	567
Maximum branch order	18	26	21	23
Number of dendritic terminals	307	274	349	568
Total dendritic length (μm)	4041	3538	5048	9854
Average dendritic path length (soma-tip; μm)	103.1	117.7	135.0	159.5
Maximum dendritic path length (μm)	166.4	181.5	204.5	269.1
Total dendritic surface area (μm2)**	46 307	34 366	109 421	180 780
Dendritic/somatic surface area	44.5	36.6	88.2	110.6
Total spine surface area (μm2)	32 062	23 627	86 797	144 267
Length of ‘spiny dendrites’ (μm)	3855	3375	4704	9474
Surface area of ‘spiny dendrites’ (μm2)**	44 454	32 685	106 120	176 664
Surface area of ‘smooth dendrites’ (μm2)**	1853	1681	3301	4116
Ratio of ‘spiny’/‘smooth’ surface area	24.0	19.4	32.1	42.9
Axon
Total number of axonal compartments	29	10	285	293
Total axonal length (μm)	148	47	1087	1282
Total axonal surface area (μm2)	500	111	1904	2673

^*Measured from the origin of the dendrite;

^**including spines

Spine densities

Spines were incorporated by scaling membrane capacitance and conductances (Shelton, 1985; Holmes, 1989). Regions of high spine density in the spiny branchlets, and low spine density along the main dendrites were delineated by visual inspection of each cell in the light microscope (LM). In the spiny branchlets, spine counts in LM indicated that spine densities per dendritic length were proportional to the mean dendritic diameter (see also Larkman, 1991, his Fig. 3), suggesting that spine density per dendritic shaft area is approximately constant. However, in absolute terms spine densities estimated in LM were, as expected, lower than those obtained from electron microscopic (EM) studies (Harris & Stevens, 1988; Napper & Harvey, 1988). Thus, to calculate scale factors for C_m and 1/R_m in the spiny branchlets of the older cells (Cell 3 and Cell 4), we used spine densities from Harris & Stevens (1988, their Fig. 2). Scale factors were given by F = (N_spine A _spine +π dl)/(πdl), where N_spine is the number of spine origins on a reconstructed dendritic segment, A_spine (= 1.12 μm²) is the mean membrane area of a spine (Harris & Stevens, 1988), and d and l are the mean diameter and length of the dendritic segment, respectively. The mean scale factor, calculated for the dendritic segments reconstructed by Harris & Stevens (1988), was 5.34. For the P14 cells (Cell 1 and Cell 2), we used spine counts from a 3-D reconstruction of a P14 Purkinje cell spiny branchlet obtained from serial ultrathin sections (A. Roth, Z. Nusser & M. Häusser, unpublished data), yielding a scale factor of 3.5. In regions of low spine density along the main dendrites, the scale factor was 1.2 throughout, corresponding to ∼2 spines per micrometre (R. J. Harvey, personal communication). Some axonal sections in Cell 4 were unstained and assumed to be myelinated. Thus, membrane capacitance and conductances in these sections were reduced by a factor of 10 to account for myelination.

Figure 3. Direct fits of impulse responses.

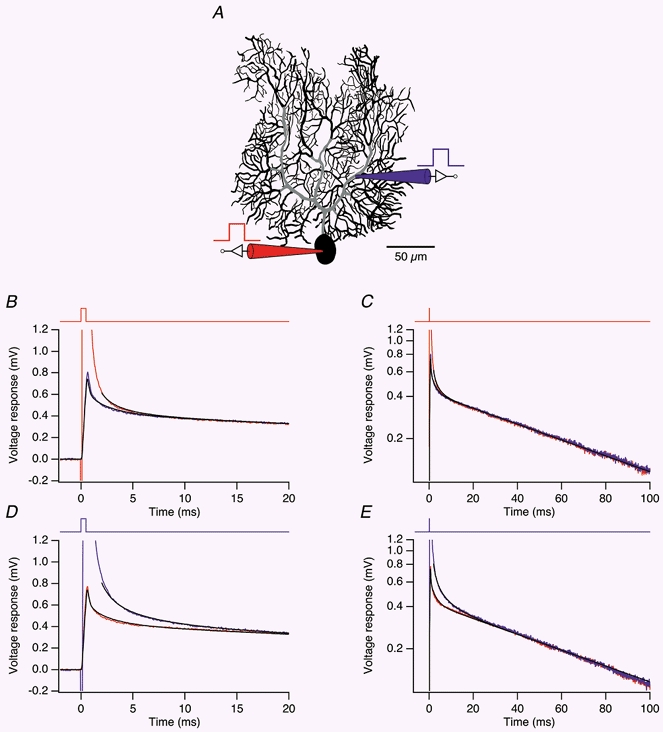
A, morphological reconstruction of the dendritic arbor of Cell 4. Regions of low spine density along the main dendrites (see Methods) are indicated in grey. Positions of the somatic (red) and dendritic recording pipette (blue) are shown symbolically. B, average somatic (red) and dendritic (blue) voltage responses measured in the cell shown in A in response to somatic current pulses (0.5 ms, +1 nA, time course shown at the top of the panel). The somatic and dendritic voltage responses to the same current pulse, simulated in the model with best-fit parameters, are superimposed (black traces). To skip the pipette artifact, the fit of the somatic trace starts 2 ms after the beginning of the current pulse. C, same transients as in B, but plotted with logarithmic voltage scale over the entire fit interval (100 ms). D, average dendritic (blue) and somatic (red) voltage responses to dendritic current pulses (same parameters as in B). Responses simulated in the model with best-fit parameters are superimposed in black. The fit of the dendritic voltage response starts 2 ms after the beginning of the current pulse. E, same traces as in D, plotted semilogarithmically.

Figure 2. Three-dimensional reconstructions of rat Purkinje cells.

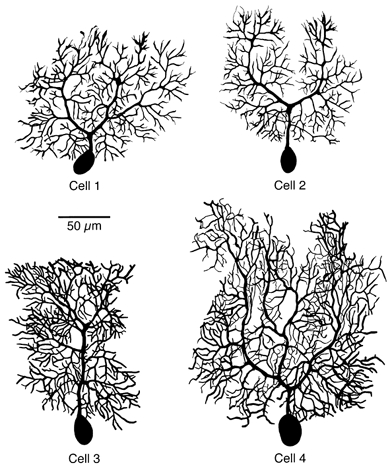
Two-dimensional projections of the three-dimensional digital reconstructions of the four cells selected for modelling. Cell 1 and Cell 2 were from 14-day-old, Cell 3 from 15-day-old and Cell 4 from 21-day-old animals. Axons, which were also reconstructed, are omitted for clarity.

Pipette models

Optimal capacitance compensation is expected to cancel the effects of most of the pipette capacitance. However, the capacitance of the pipette tip remains largely uncompensated due to series resistance (Thurbon et al. 1998). Therefore, the pipette tips were included explicitly in the compartmental model. Somatic pipette tips were modelled as a conical arrangement of sections, with an initial diameter of 2 μm, a final diameter of 256 μm, and a total length of 2.55 mm (cf. Major et al. 1994). They were subdivided into 80 compartments. Dendritic pipette tips were constructed analogously, but diameters were reduced by a factor of 1.58. The value of R_i in each pipette model was chosen such that the series resistance of the model matched the series resistance of the respective pipette in the experiment, as determined from the setting of the bridge balance during collection of impulse responses. The capacitance per unit length of each pipette was assumed to be constant, as would be expected if the local wall thickness of the pipette tip is scaled proportional to the local outer diameter (Sakmann & Neher, 1995). Values of this parameter for each pipette model (range, 0.15-1.75 pF mm⁻¹) were estimated by including it in direct fits of impulse responses (see below). The conductivity of the pipette wall was assumed to be zero.

Direct fitting

The free parameters of the compartmental models, usually C_m, R_m and R_i, were determined simultaneously by direct fitting of the averaged impulse responses measured experimentally in the same cell (Clements & Redman, 1989; Major et al. 1994; Stuart & Spruston, 1998; Thurbon et al. 1998). The baseline of the averaged experimental responses was determined over a 50 ms period ending 6.5 ms before the beginning of the impulse and then subtracted from the experimental average. Squared differences between impulse responses predicted by the model and those measured experimentally were minimized using a multidimensional optimization method built into NEURON. The algorithm, PRAXIS, uses the principal axis method (Brent, 1973; Press et al. 1992) to efficiently solve non-linear fit problems in which some parameters are strongly correlated or anticorrelated (such as C_m and R_m).

To account for low-pass filtering of the experimental responses, model responses were convolved with a Gaussian filter kernel corresponding to a cutoff frequency of 4.93 kHz (Colquhoun & Sigworth, 1995). Local voltage responses, measured by the electrode injecting a current pulse, and transfer responses to both somatic and dendritic current injection were fitted simultaneously, unless specified differently. The standard fit interval started with the beginning of the current pulse and ended 100 ms later, except for local responses where it started 2 ms after the beginning of the current pulse to avoid pipette artifacts due to the large voltage drop across the current-injecting electrode (Major et al. 1994). Fits were tested for convergence by restarting them with different sets of initial parameter values. In addition, at the end of each fit a grid search was performed by independently varying the fit parameters by ± 0.1 % around their best-fit values.

Statistical and systematic errors

Statistical errors in the best-fit parameters were estimated by balanced resampling of the measured traces (Efron & Tibshirani, 1993). Each pair of local and transfer responses to a somatic or dendritic current pulse was indexed by an integer from 1 to n_soma or 1 to n_dend, respectively, where n_soma is the number of somatic current pulses, and n_dend is the number of dendritic current pulses for which pairs of experimental impulse responses were available (in our experiments, n_soma ranged from 55 to 343 and n_dend from 36 to 351). The index sets for the original averages were then given by the range of all integers from 1 to n_soma and 1 to n_dend. To generate 100 synthetic, resampled data sets, these index sets were repeated 100 times each to form two lists of length 100 ×n_soma and 100 ×n_dend. Random permutations were applied to these lists, such that each index still occurred 100 times in each list, but at random positions. Finally, each list was partitioned into 100 sublists of length n_soma and n_dend, respectively, each sublist representing an index set for a resampled average impulse response (see also Supplementary material on the website; http://jphysiol.org/cgi/content/full/535/2/445). After baseline subtraction, resampled averages were fitted in NEURON with the same procedure as the original averages, yielding 100 parameter sets for C_m, R_m and R_i, whose distribution is an estimate of the distribution of statistical errors in the original best-fit parameters. To estimate the influence of these errors on predictions of the model, such as the attenuation of EPSCs originating in the dendrites recorded by somatic voltage clamp, EPSCs were simulated (see below) for five synaptic locations (illustrated in Fig. 6A and D) in each cell for each of the 100 parameter sets, and the distribution of EPSC peak amplitudes and half-widths was determined for each synaptic location.

Figure 6. Dendritic regions corresponding to the two compartments of the reduced model.

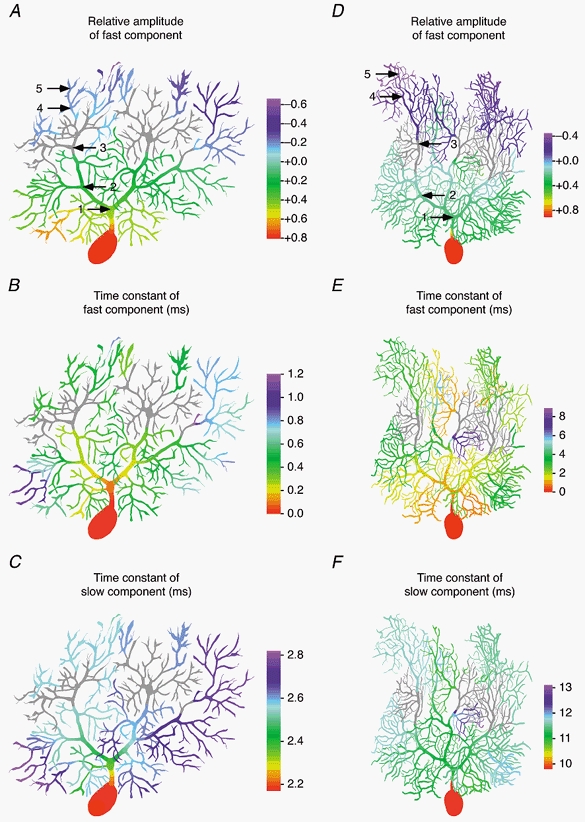
Voltage responses to a 10 mV somatic voltage-clamp step were simulated as in Fig. 5. The voltage response in each dendritic compartment was recorded and fitted with up to two exponentials in DISCRETE. The fit interval (95 ms) started at the time of the voltage-clamp step. A-C, colour-coded representation of the relative amplitude of the fast exponential, the time constant of the fast exponential, and the time constant of the slow exponential of double-exponential fits obtained with DISCRETE for each dendritic compartment of Cell 1. In the grey regions, the voltage response was classified as single exponential, either because DISCRETE reported a single exponential as the best solution, because the fast and slow time constants differed by less than 1 ms, or because the relative amplitude of the fast exponential was between -10 and +10 %. A negative amplitude of the fast exponential indicates a delayed onset of the voltage response (see Fig. 5A, traces 4 and 5). D-F, same as A-C but simulated in the model of Cell 4. Voltage responses were classified as single exponential (grey) if DISCRETE reported this as the best solution, if the fast and slow time constants differed by less than 3 ms, or if the relative amplitude of the fast exponential was between -10 and +10 %. Colour bars, 100 μm.

The influence of possible systematic errors on best-fit model parameters and predictions was investigated in a similar way. The eight most likely independent sources of systematic errors were considered. Error variables were assumed to be normally distributed around the mean given by the original morphology and pipette models, with standard deviations estimated according to the expected experimental uncertainties (Table 1).

Table 1.

Sources of systematic errors

Error variable	Estimated S.D.
Scale factor for lengths in the morphological reconstruction	0.05
Additive error in reconstructed diameters (μm)	0.3
Multiplicative error in reconstructed diameters	0.1
Error in spine scale factor in regions of low spine density	0.1
Error in spine scale factor in regions of high spine density	1.0
Position of dendritic recording pipette (μm)	1.0
Capacitance of somatic pipette tip (pF mm−1)	0.15
Capacitance of dendritic pipette tip (pF mm−1)	0.15

Normally distributed random numbers were used to generate 100 sets of error variables according to Table 1. Physical constraints were imposed such that lengths, capacitances, spine densities and diameters were positive. For each set of error variables, modified morphologies and pipette models were constructed, and the original average impulse responses were fitted in NEURON, yielding 100 parameter sets for C_m, R_m and R_i whose distribution gives an estimate of the systematic errors in the original best-fit parameters. To estimate the influence of systematic errors on predictions of the model, again EPSCs were simulated for five synaptic locations in each cell for each of the modified morphologies with its best-fit values of C_m, R_m and R_i, and the distribution of EPSC peak amplitudes and half-widths was determined for each synaptic location. Mathematica 4 (Wolfram Research, Champaign, IL, USA) was used in all operations involving random numbers, for automatic code generation for NEURON, and in the analysis of the distributions of statistical and systematic errors.

Voltage-clamp simulations

Somatic voltage clamp was simulated in NEURON assuming a residual uncompensated series resistance of 1 MΩ. Cells were clamped at their resting potential (-70 mV) unless specified differently. Multiexponential fits of somatic clamp currents and dendritic voltage responses were done using DISCRETE 2B (Provencher & Vogel, 1980), a program for the automatic analysis of discrete sums of exponential decays. DISCRETE is capable of fitting sums of up to nine exponentials and can automatically determine the number of exponentials most likely to describe the data based on a modified F test.

Synaptic conductances activated by single parallel fibre (PF) inputs were simulated as a sum of two exponentials, one for the rise (0.2 ms) and one for the decay (3 ms) unless otherwise indicated. The peak conductance was 1 nS, and the synaptic reversal potential was 0 mV. To simulate the synaptic conductance activated by the climbing fibre (CF), 500 of these conductances (Silver et al. 1998) were placed on the main dendrites (grey region in Fig. 3A), in agreement with the known distribution of CF contacts, at a constant density per dendritic length.

Single-exponential fits of the decay of EPSCs recorded at the soma were performed in NEURON. The fit interval (length, ∼5 decay time constants) started at the time point after the peak where the EPSC had decayed to 95 % of its peak amplitude. DISCRETE was used to fit the rise and decay phases simultaneously with a double exponential, one for the rise and one for the decay. The fit interval of the double-exponential fits started at the time point before the peak where the EPSC had reached 50 % of its peak amplitude, and ended at the same time point as the interval for the single-exponential fits.

Modelling I_h

A Hodgkin-Huxley-type model of the hyperpolarization-activated current, I_h, was constructed in Mathematica and implemented in NEURON. Activation and deactivation of the conductance underlying I_h was described by a single gating variable, h, according to (Hodgkin & Huxley, 1952):

where t is time. The rate constant for activation (α) is given by:

and the rate constant for deactivation (β) is given by:

V is the membrane potential. The free parameters of the model, a, b, c and V_1/2, were determined by fitting the experimentally measured voltage dependence of the steady-state activation, h_∞, and the time constant of activation or deactivation, τ, which in terms of the model are given by:

and

Fitting was done using the FindMinimum function built into Mathematica. Data points were first weighted by the inverse of their variance. Then, to ensure that the steady-state activation is well represented by the model, the weight of the data points of the steady-state activation curve was increased by a factor of 10. The model with best-fit parameters was implemented in NMODL (Hines & Carnevale, 2000) and inserted into the passive Purkinje cell models in NEURON. The density of the conductance underlying I_h, which was assumed to be homogeneous, was calibrated by fitting experimental voltage responses to long (1.5 s) somatic current pulses.

RESULTS

Electrophysiology

Whole-cell patch-clamp recordings were made from Purkinje cells in sagittal slices of cerebellar cortex in order to preserve the integrity of the dendritic architecture. Purkinje cells are spontaneously active even in the absence of excitatory synaptic input (Rapp et al. 1994; Häusser & Clark, 1997; Raman & Bean, 1999), and therefore constant hyperpolarizing current was used to hold neurons below action potential threshold. At subthreshold potentials, the membrane behaviour of Purkinje cells is dominated by the hyperpolarization-activated cation current, I_h, which causes a pronounced time-dependent rectification, or ‘sag’, in response to injection of hyperpolarizing or depolarizing currents (Crepel & Penit-Soria, 1986; Rapp et al. 1994). Bath application of the selective I_h blocker ZD 7288 (Harris & Constanti, 1995) completely abolished sag (Fig. 1A). In control conditions the extent of sag measured in responses to long current steps at the soma was 0.59 ± 0.10 (n = 11; ratio of steady-state vs. peak voltage response), while in ZD 7288 (30-50 μm) no sag was detectable. Blocking I_h also hyperpolarized the neurons to a resting potential of -73.6 ± 7.3 mV, and caused a dramatic increase in the input resistance and membrane time constant of the Purkinje cells. In control conditions, the peak and steady-state input resistance was 106.2 ± 51.9 and 59.3 ± 38.4 MΩ, respectively, while in ZD 7288 the input resistance was 267.8 ± 157.5 MΩ. The apparent membrane time constant (τ_m) estimated from the responses to brief (0.5 ms) current injections, was 64.6 ± 17.2 ms in control conditions and 116.9 ± 56.1 ms in the presence of ZD 7288. As I_h thus affected the responses to both short and long current pulses, experiments to determine the parameters of passive compartmental models were performed in the presence of ZD 7288. The biophysical properties of I_h were determined separately (see below) in order to later incorporate this conductance into the model.

Figure 1. Linearity and reciprocity of voltage responses in Purkinje cells with I_h blocked.

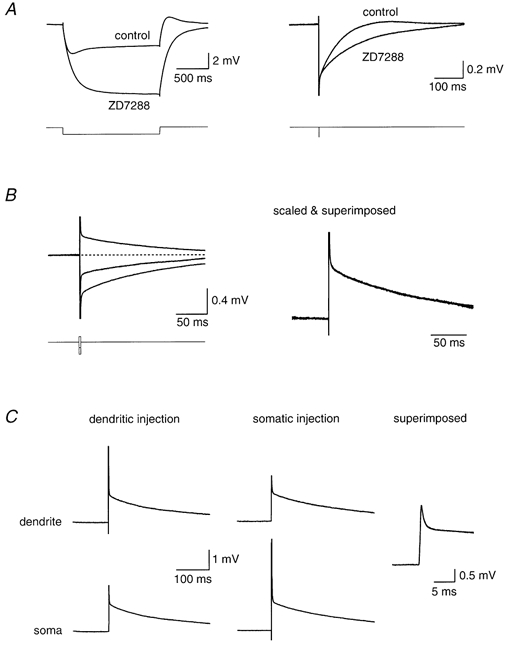
A, somatic recording from a cerebellar Purkinje cell, injecting a long (1.5 s) or brief (0.5 ms) hyperpolarizing current pulse under control conditions or in the presence of 50 μm ZD 7288. B, somatic recording from the same Purkinje cell as in A, injecting brief (0.5 ms) current pulses of different polarity and amplitude. The response to three pulses is shown: -1.0, -0.5 and +0.5 nA. The right-hand panels show the superimposed traces after normalizing by the injected current. C, simultaneous somatic and dendritic recording (75 μm from the soma), injecting a -1.0 nA brief (0.5 ms) current pulse either at the dendritic (left panel) or somatic (centre panel) electrode (traces have been inverted). The right-hand panel shows a superimposition of the traces from the somatic and dendritic recording site when the same current pulse is applied via the independent electrode.

Simultaneous somatic and dendritic recordings were made in order to measure attenuation of voltage between two locations in the Purkinje cell (Stuart & Häusser, 1994). In the presence of ZD 7288, attenuation of steady-state membrane potential was slight (< 5 %), even at the most remote dendritic recording locations (> 150 μm from the soma). Since this is within the measurement error for determining bridge balance for the injecting electrode, this made it difficult to use the steady-state attenuation to accurately determine the intracellular resistivity (Stuart & Spruston, 1998). We therefore examined the spread of the transient voltage response to brief (0.5 ms) current pulses injected via either the dendritic or the somatic pipette. These transients attenuated significantly between somatic and dendritic recording electrodes, even at relatively small separations (< 100 μm; Fig. 1C), thus providing a sensitive index of the electrotonic structure of the neuron (Major et al. 1993).

We performed several tests in order to verify linear behaviour of the Purkinje cells in response to these brief current injections. First, the amplitude of the current injections was varied, and the individual responses were scaled and superimposed. Second, pulses of different polarities were inverted and superimposed. Both of these tests demonstrated linear behaviour in the presence of ZD 7288 (Fig. 1B). Finally, another important test of the linear behaviour of a system is the ability to show reciprocity between two recording sites (Major et al. 1993). Responses to identical current injections at somatic and dendritic locations, recorded at the second electrode located either at the soma or in the dendrites, were superimposable (Fig. 1C), consistent with linear behaviour of the membrane under these conditions.

Morphology

Neurons were filled with biocytin during the electrophysiological recording, and then later processed to reveal their morphology. Four of these neurons were selected for complete morphological reconstruction (Fig. 2) based on the quality of both the electrophysiological and anatomical data. The four neurons chosen reflected the range of morphological and electrophysiological variation present in the whole dataset. The anatomical features of the reconstructed neurons are presented in Table 2. As described previously (Palay & Chan-Palay, 1974; Rapp et al. 1994), the dendritic tree of the Purkinje cell was elaborated almost exclusively in the sagittal plane, with the maximal variation in the z-direction being less than 50 μm. This confirms that the entire dendritic architecture of the Purkinje cell can be preserved intact in the sagittal slice preparation. All four cells had a large primary dendrite (∼4 μm diameter) which bifurcated rapidly within 40 μm from the soma, giving rise to two or more large secondary dendrites and numerous smaller branches. The extent of branching and length of the branches varied with development (Altman, 1972; Berry & Bradley, 1976), with the two younger (P14) cells having a shorter total length, fewer branches, and consequently smaller total membrane area than the more mature (P15-P21) cells. (Note that granule cell migration, which defines the depth of the molecular layer and thus the height of the Purkinje cell dendritic tree, is complete by P21, although Purkinje cells can still exhibit modest increases in number of branches after this age; Altman, 1972; Berry & Bradley, 1976.) The dendritic tree could be subdivided based on direct visual inspection into larger ‘smooth’ branches with few spines (grey region in Fig. 3A), corresponding to the termination zone of climbing fibre (CF) contacts (Palay & Chan-Palay, 1974), and the smaller ‘spiny branchlets’, corresponding to the innervation zone of the parallel fibres (PF). The spiny branchlets comprised the overwhelming majority of the dendritic tree, representing 95.0 ± 1.3 % of total dendritic length and 96.5 ± 1.1 % of total dendritic area (including spines). The terminal branches were all of the spiny branchlet type. Interestingly, in the younger (P14) cells some terminal branches ended in thin filaments, probably corresponding to the motile filopodia recently observed in imaging studies (Jontes & Smith, 2000).

Compartmental models

Compartmental models of the four Purkinje neurons were constructed by combining morphological and electrophysiological data from the same cell. The reconstructed morphology, including the axon, was imported directly into NEURON, and spines were incorporated into the model by scaling membrane capacitance and conductances where appropriate (Shelton, 1985; Holmes, 1989; see Methods). Voltage responses to brief (0.5 ms) current pulses (Major et al. 1994) injected either by the somatic or dendritic recording pipette were then used to probe the free parameters of the model, C_m, R_m and R_i.

Direct fitting

The standard fit procedure is illustrated in Fig. 3. Best-fit values of C_m, R_m and R_i were determined simultaneously by direct fitting of impulse responses (see Methods). To use as much information about the passive structure of the cell as possible, four voltage responses were fitted simultaneously with equal weight: the somatic and dendritic voltage response to somatic current pulses (Fig. 3B and C) and the somatic and dendritic voltage response to dendritic current pulses (Fig. 3D and E). Note that the transfer responses are identical in a linear system, and thus in theory they do not provide independent constraints for a passive model, but in practice they cause the fitted response to interpolate between them. In most cases the fits converged easily to a local minimum in the χ² function, even for poor choices of starting values. The fitted responses (black lines in Fig. 3B-E) superimpose well with the experimentally measured responses, confirming that under these conditions, the cell is well described by a passive compartmental model with uniform parameters. Using this standard fit procedure, C_m was 0.77 ± 0.17 μF cm⁻² (n = 4), R_m was 122 ± 18 kΩ cm² and R_i was 115 ± 20 Ω cm.

Which features in the data constrain which parameter, and why do the fits converge easily? In the semilogarithmic plots of somatic and dendritic voltage responses (Fig. 3C and E) two phases can be distinguished. In the first phase, which is characterized by a difference between the voltages recorded at the somatic and dendritic recording sites, charge injected via an electrode is redistributed within the cell. In the second phase, in which somatic and dendritic voltage are approximately equal, the membrane potential decays homogeneously back to the resting potential with time constant τ_m=R_mC_m. The two phases were well separated in Purkinje cells as charge redistribution lasted only a few milliseconds (up to 20 ms for dendritic current injection; Fig. 3D and E) while τ_m was 94 ± 31 ms in the four selected cells under passive conditions (see Table 3). From the second phase, the product τ_m=R_mC_m was very well constrained. Its individual factors were also well constrained as C_m can be estimated by extrapolating the voltage response of the second phase back to the time of the end of the current pulse, when all charge has entered the cell and C_m is determined by the ratio of charge and (monoexponentially extrapolated) voltage response. Finally, the single remaining free parameter, R_i, was constrained by both the amplitudes and the time courses of the voltage responses during the first phase. Thus, each of the free parameters was well constrained by independent features in the data, and the fits did not suffer from nonuniqueness.

Table 3.

Best-fit model parameters, and estimated statistical and systematic errors

	Cell 1			Cell 2			Cell 3			Cell 4
	Best fit	S.D. stat	S.D. sys	Best fit	S.D. stat	S.D. sys	Best fit	S.D. stat	S.D. sys	Best fit	S.D. stat	S.D. sys
All available data
Cm (μF cm−2)	0.78	0.01	0.40	1.00	0.01	0.54	0.66	0.00	0.23	0.64	0.01	0.25
Rm(kΩ cm2)	97.8	5.5	38.2	141.0	4.6	58.4	127.0	2.8	37.2	120.2	3.2	38.7
Ri(Ω cm)	113.6	4.7	40.7	112.1	1.5	36.7	92.9	1.8	26.4	141.9	3.4	36.0
τm(ms)	76.3	4.3	0.1	141.4	4.7	0.4	83.4	1.8	0.3	76.8	2.0	0.6
EPSC(pA)*	−32.43	0.73	1.98	−25.80	0.23	1.74	−20.11	0.25	2.28	−10.75	0.24	0.37
Somatic electrode only
Cm(μF cm−2)	0.78	0.01	0.40	0.99	0.01	0.53	0.67	0.01	0.23	0.65	0.01	0.26
Rm(kΩ cm2)	98.8	5.6	38.5	134.1	4.8	55.6	128.9	4.5	37.8	120.6	5.1	38.8
Ri(Ω cm)	154.6	11.3	47.6	159.1	3.4	50.0	100.0	2.6	23.9	139.9	4.8	36.9
τm(ms)	76.6	4.4	0.1	133.0	4.9	0.3	86.1	3.2	0.1	78.5	3.3	0.5
EPSC(pA)*	−28.31	1.16	1.27	−21.71	0.30	1.82	−19.06	0.36	0.21	−10.71	0.35	0.33

^*Somatic amplitude of a simulated EPSC arising from a dendritic location corresponding to that labelled ‘3’ in Fig. 6A and D (see Methods).

Variations of the standard fit procedure

To assess the robustness of the model, and to test alternative models, several modifications to the fit procedure were tested. When only somatic voltage responses to somatic current pulses were fitted, C_m was 0.77 ± 0.16 μF cm⁻² (n = 4), R_m was 121 ± 16 kΩ cm² and R_i was 138 ± 27 Ω cm (see also Table 3). When the first 2 ms after the beginning of the current pulse were skipped also in the transfer responses, as they may also suffer from pipette artifacts (Thurbon et al. 1998), C_m was 0.77 ± 0.17 μF cm⁻² (n = 4), R_m was 122 ± 18 kΩ cm² and R_i was 131 ± 27 Ω cm. Thus, fits to part of the available experimental data gave similar results as the standard fits, confirming the consistency of the model. Changes to the spine density in spiny branchlets were tested for Cell 3 (P15). When it was fitted with P14 spine densities, C_m was scaled up and R_m was scaled down by a factor of 1.48 as expected for this change of effective membrane area, to 0.97 μF cm⁻² and 86 kΩ cm², respectively, but R_i was 94 Ω cm, very similar to the standard value for this cell of 93 Ω cm (see Table 3).

Error analysis

Both statistical and systematic errors may be responsible for the differences in the values of the best-fit parameters obtained with variations of the standard fit procedure. Statistical errors due to noise in the experimentally measured voltage responses were estimated by the bootstrap method (Press et al. 1992; Efron & Tibshirani, 1993), which involves creation of synthetic average voltage responses by resampling the original sweeps (see Methods). Using the standard fit procedure, relative errors (estimated s.d./mean) were estimated to be less than 6 % in any fit parameter in any cell (Table 3). The mean relative error was 0.9 % in C_m (range, 0.4-1.6 %; n = 4), 3.5 % in R_m (range, 2.2-5.7 %) and 2.5 % in R_i (range, 1.3-4.1 %). The effect of statistical errors on predictions of the model, such as the somatic amplitude of simulated EPSCs arising from a dendritic location, was also small. For a typical synaptic location, e.g. that labelled ‘3′ in Fig. 6A and D, the mean relative error was only 1.6 % (range, 0.9-2.2 %). However, a slight increase in the relative error in R_i was observed when only somatic voltage responses to somatic current pulses were included in the fits during the bootstrap procedure, indicating that R_i is more susceptible to experimental noise when data from a single somatic electrode are used for fitting.

In contrast to statistical errors, systematic errors (Table 1; see Discussion) had the major effect on the best-fit model parameters. With the standard fit procedure, the mean relative error was 45 % in C_m (range, 35-54 %; n = 4) and 35 % in R_m (range, 29-41 %; see Table 3). This is expected, e.g. since large changes in spine density, one of the assumed sources of systematic errors (Table 1), imply large changes in the effective membrane area of a cell, which are then compensated by rescaling C_m and R_m. However, the membrane time constant, τ_m=R_mC_m, was little affected by systematic errors (mean relative error, 0.4 %; range, 0.2-0.8 %). Thus, while ‘raw’ model parameters (Major et al. 1994) such as C_m and R_m were severely affected by systematic errors, ‘core’ model properties like τ_m were much more reliable. The mean relative error in the third raw fit parameter, R_i, was 31 % (range, 25-36 %), similar to the errors in C_m and R_m. The core model as a whole, however, was less affected as judged by the prediction for the somatic amplitude of simulated EPSCs, whose mean relative error was only 6.9 % (range, 3.4-11.3 %). In conclusion, if morphological data and impulse responses from the same cell are used for building a passive model, the core model properties as well as predictions of the model may be more accurate than suggested by the errors in the raw model parameters C_m, R_m, R_i and the morphology of the cell (Major et al. 1994).

The relative influence of the various sources of systematic errors (Table 1) on the best-fit parameters was assessed by calculating the Pearson correlation coefficient r between the (random) setting of an error variable and the value of a best-fit model parameter across the 100 sets of error variables (see Methods). The best-fit value of R_i, for example, was strongly correlated with additive and multiplicative errors in the reconstructed diameters. With the standard fit procedure, the mean value of r for the four cells was 0.69 (range, 0.63-0.74) for additive errors, and 0.51 (range, 0.43-0.61) for multiplicative errors in diameter. Interestingly, R_i was affected only weakly by the other sources of systematic errors (|r| < 0.17 in any of the four cells). When only somatic voltage responses to somatic current pulses were fitted, r was 0.69 (range, 0.56-0.77) for additive errors, and 0.54 (range, 0.43-0.68) for multiplicative errors, very similar to the correlation coefficients obtained with the standard fit procedure, in which both somatic and dendritic voltage responses were used for fitting. Again, all other sources of systematic errors had only a weak influence on R_i (|r| < 0.17 in any of the four cells).

In contrast to statistical errors, systematic errors generally had a similar influence on the best-fit model parameters as well as the predicted somatic amplitude of simulated EPSCs both for the standard fit of all available data and the restricted fit of data obtainable with a single somatic electrode only. This is summarized in Table 3, which illustrates that the differences in the values of the best-fit parameters obtained with variations of the standard fit procedure (see above) are consistent with the size of the estimated systematic errors.

Steady-state electrotonic structure of Purkinje cells

The dendritic tree of Purkinje cells is characterized by an extremely high density of branch points (0.14 ± 0.02 μm⁻¹; range, 0.12-0.15 μm⁻¹; n = 4). The branching density was similar on the main dendrites and in the region of the spiny branchlets. The length of individual spiny branchlets (including their terminal segments) is relatively short, such that the tip of the spiny branchlet is typically only < 50 μm from its parent main dendrite.

The diameter of the main dendrites is large compared to that of the spiny branchlets. Together with the high branching density, this results in a pronounced asymmetry between the steady-state voltage attenuation in the somatofugal (soma → dendrite; Fig. 4A) and somatopetal (dendrite → soma; Fig. 4B) direction. The steady-state voltage control of the dendritic tips from the soma is very good, especially for P14 Purkinje cells (mean attenuation factor, 0.97; Table 4; Fig. 4A). Most of the voltage drop occurs within the main dendrites; there is little attenuation from a given location on a main dendrite to the terminal tips of the local spiny branchlets connected to it. Thus, steady-state voltage control of Purkinje cell dendrites from the soma decayed relatively uniformly with location in the molecular layer from the Purkinje cell layer to the pia. In contrast, the steady-state voltage control of the soma from the dendritic tips is poor, especially at P21 (mean attenuation factor, 0.43; Table 4; Fig. 4B). For distal inputs, most of the voltage drop occurs in the thin spiny branchlets. The attenuation within the thicker main dendrites is small, particularly in the proximal main dendrites where attenuation in the somatopetal direction is even smaller than in the somatofugal direction. This means that somatopetal attenuation is best described as a function of distance from the soma, measured along the dendritic branches, rather than a function of distance from the pia.

Figure 4. Steady-state voltage attenuation.

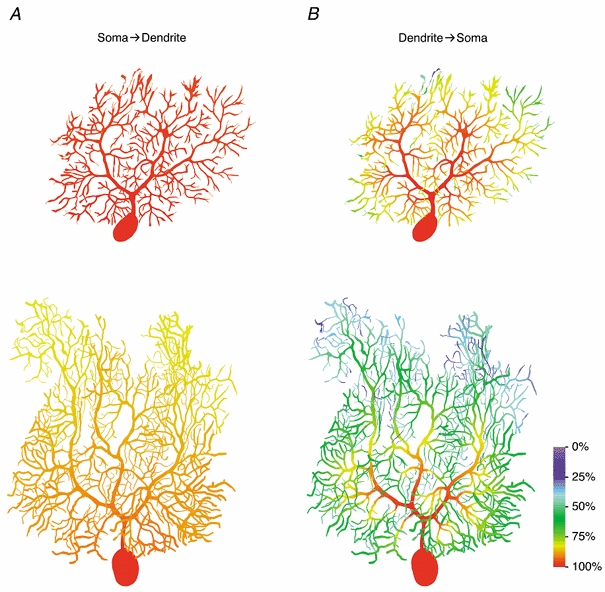
A, colour-coded representation of steady-state voltage control of the dendrites by a voltage-clamp electrode located at the centre of the soma, simulated in the best-fit passive models of Cell 1 and Cell 4. Each dendritic location is coloured according to the value of (V_local - V_rest)/(V_soma - V_rest) × 100 %, where V_local is the membrane potential at that location, V_rest is the resting potential of the cell (-70 mV), and V_soma is the membrane potential at the centre of the soma, imposed by the somatic voltage-clamp electrode. B, colour-coded representation of steady-state voltage control of the soma from various dendritic locations. Same models as in A. Each dendritic location is coloured according to the value of (V_soma - V_rest)/(V_local - V_rest) × 100 %, where V_local is the local membrane potential imposed by the dendritic voltage-clamp electrode, and V_soma is the membrane potential at the centre of the soma. Colour bar, 100 μm.

Table 4.

Predicted electrotonic structure

	Cell 1	Cell 2	Cell 3	Cell 4
Average electrotonic path length	0.074	0.070	0.071	0.123
Average attenuation factor soma → tips	0.972	0.973	0.942	0.864
Average attenuation factor tips → soma	0.749	0.792	0.794	0.431
Asymmetry index*	0.771	0.814	0.843	0.499
Average terminal input resistance(MΩ)	280.5	511.1	142.3	167.1
Somatic input resistance(MΩ)	210.1	408.9	119.6	75.1
Total cell capacitance(pF)	373.3	355.0	738.8	1177

^*Average attenuation factor tips → soma/average attenuation factor soma → tips.

Comparison with a reduced model of Purkinje cells

Llano et al. (1991) proposed a two-compartment model for Purkinje cells based on their analysis of somatic voltage-clamp recordings. They demonstrated that the capacitive current measured in response to somatic voltage steps can (in some cases) be satisfactorily fitted by a sum of two exponentials, and interpreted these components using an equivalent electrical circuit comprising two compartments. They used this model to evaluate the quality of space-clamp in their experimental measurements of EPSCs. We tested this model by comparing it with our detailed compartmental models.

We first tested the assumption that the decay phase of capacitive currents resulting from somatic voltage-clamp steps in Purkinje cells can be fitted by the sum of two exponentials. Capacitive transients in response to +10 mV somatic voltage-clamp steps in the models of Cell 1 and Cell 4 are shown in Fig. 5B and D, respectively. Double-exponential fits of the transient of Cell 1 looked acceptable, but fits for Cell 4 clearly deviated from the transient (see insets). However, unlike simulated transients, experimentally measured capacitive transients are noisy, and whether a description by a sum of two exponentials is statistically adequate will depend on both the shape of the underlying transient and the noise level. Therefore we added Gaussian noise (s.d., 6.5 pA) to the simulated transients and used the program DISCRETE (Provencher & Vogel, 1980) to statistically determine the number of exponentials necessary to fit the data. DISCRETE fits showed that for both cells, a sum of five exponentials was the best solution. The approximate probability that this solution was better than the second-best solution (4 exponentials) was given as 1.000 in both cases. When the series resistance was increased from the standard value of 1 MΩ to 7 MΩ, i.e. when series resistance compensation was effectively ‘turned off’, a sum of five exponentials was still the best solution for Cell 1, while a sum of four exponentials was reported as the best solution for Cell 4. Here, the approximate probability that four exponentials were a better description of the data than the second-best solution (5 exponentials) was 0.999. This indicates that, particularly for the older Purkinje cells, the basic assumption required to construct the two-compartment model does not hold.

Figure 5. Comparison with a reduced, two-compartment model of Purkinje cells.

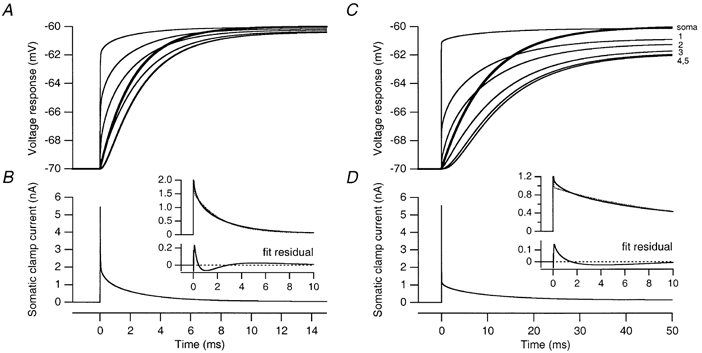
A, voltage responses (thin lines) at the soma and at five dendritic locations (indicated by arrows in Fig. 6A) to a 10 mV somatic voltage-clamp step in the best-fit passive model of Cell 1. The prediction (thick line; τ′₂= 2.18 ms) of the two-compartment model of Llano et al. (1991) is shown superimposed. B, somatic clamp current injected during the voltage-clamp step shown in A. The truncated clamp current waveform (continuous line) is shown again in the upper panel of the inset, together with a double-exponential fit (dotted line) of its decay phase. The corresponding fit residual is shown in the lower panel of the inset. C, voltage responses (thin lines) at the soma and at five dendritic locations (indicated by arrows in Fig. 6D) to a 10 mV somatic voltage-clamp step in the best-fit passive model of Cell 4. The thick line represents the prediction of the two-compartment model (τ′₂= 9.83 ms). D, somatic clamp current injected during the protocol shown in C. The truncated clamp current waveform (continuous line) is shown again in the upper panel of the inset, together with a double-exponential fit (dotted line) of its decay phase. The corresponding fit residual is shown in the lower panel of the inset.

We next compared the time course of dendritic voltage changes in response to the somatic voltage-clamp step predicted by the two-compartment model with those in the detailed compartmental models. The voltage response at the soma and at five dendritic locations in Cell 1 and Cell 4 is shown in Fig. 5A and C, respectively. As expected, the overall time course of the voltage response was slower at more distal dendritic sites, as the amplitude of its initial fast component became smaller and even negative for the most distal locations. In the two-compartment model, the voltage response in the distal compartment is described by a single exponential with a time constant given by the slow time constant of the somatic capacitive transient (τ′₂, as determined using double-exponential fits of the capacitive transient shown in Fig. 5B and D; Llano et al. 1991). The time course of this prediction (thick lines) is comparable to that of the transients observed in the detailed models at intermediate distances from the soma.

The detailed spatial distribution of the time course of the dendritic voltage response is shown in Fig. 6, which maps the results of double-exponential fits of the voltage response at each dendritic location. This provides an indication of the physical equivalents of the two compartments of the reduced model. The figure illustrates that the fast component of the somatic capacitive current predominates (relative amplitude > 50 %) only in the first 50 μm of the dendritic tree, and thus corresponds to the charging of the soma and the primary dendritic trunk up to the first branch point. The slow component predominates at intermediate distances (grey regions in Fig. 6). In the distal dendrites a fast component reappears, but with a negative amplitude (sigmoidal onset Fig. 5A and C, traces 4 and 5). Somewhat surprisingly, there is no clear gradient between the main dendrites and the adjacent spiny branchlets. Moreover, when examining the time constant of the slow component of the dendritic response, considerable differences were observed between the time constant and amplitude of components in different parts of the dendritic tree. For example, in the P14 neuron, over 50 % differences were observed for the kinetics of voltage responses in the terminal segments of proximal and distal spiny branchlets. Interestingly, as for the steady-state voltage control of the dendrite from the soma (Fig. 4A), the relative amplitude of the fast component, but not the time constants, appeared to be well described by a function of distance from the pia.

Space-clamp errors associated with somatic recording of quantal EPSCs

The highly filtered dendritic response to somatic voltage steps suggests that synaptic currents originating at dendritic synapses may be considerably filtered and attenuated when recorded by somatic voltage clamp. The two-compartment model predicts that if the decay time constant of the current entering the cell at a dendritic synapse is slower than the slower time constant of the capacitive current at the soma (τ′₂), then the decay of the EPSC is faithfully recorded at the soma. We tested this prediction by simulating EPSCs in the best-fit full models, using synaptic conductances with various decay kinetics at different locations in the dendritic tree, and examining the filtering of the resulting somatic voltage-clamp current. The results of these simulations are shown in Figs 7–9.

Figure 7. Attenuation of quantal EPSCs in a P14 Purkinje cell.

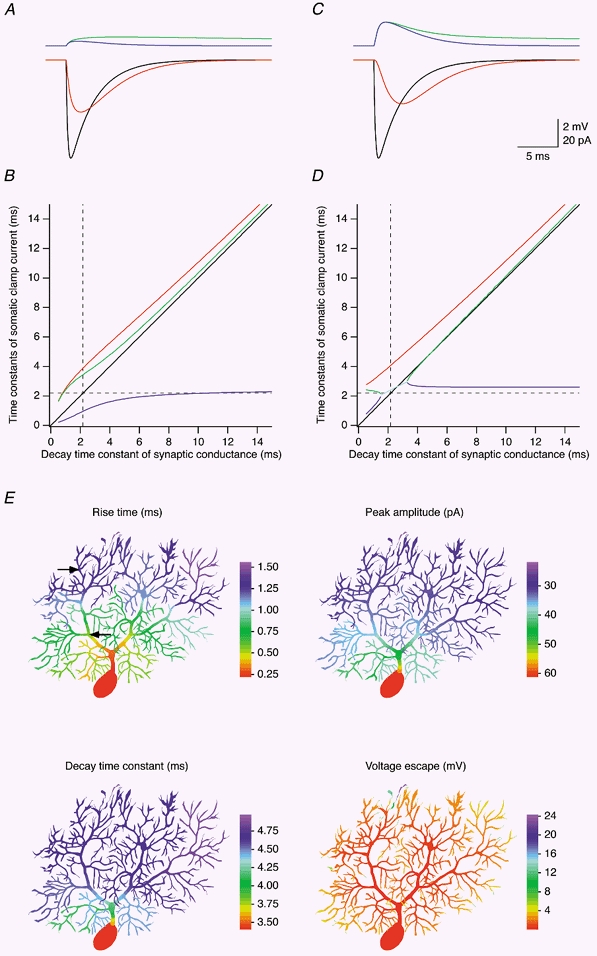
Somatic voltage clamp of EPSCs originating in the dendrites was simulated in the best-fit passive model of Cell 1. The synaptic conductance had an amplitude of 1 nS and a reversal potential of 0 mV, and its time course was described by the sum of a rising exponential (time constant, 0.2 ms) and a decaying exponential (time constant, 3 ms, unless specified differently). A, EPSC recorded at the soma (red trace), EPSC expected under conditions of ideal clamp (black trace), and local voltage escape in voltage clamp (blue trace) and current clamp (green trace) for the synaptic location indicated by the proximal arrow in E. B, relationship between time constants obtained by fitting the EPSC waveform recorded at the soma, and the decay time constant of the synaptic conductance located at the same point as in A. Red trace, single time constant fitted to the decay phase of the EPSC. Blue and green traces, rise and decay time constant of a double-exponential fit of the EPSC. The identity line is shown in black, and the value of τ′₂ (2.18 ms in the model of Cell 1) is indicated by the dashed lines. C and D, same as A and B but simulated for the synaptic location indicated by the distal arrow in E. The cyan trace in D represents the mean of the rise and decay time constants of a double-exponential fit of the EPSC in a region where the two time constants are very similar. E, colour-coded representation of the 20-80 % rise time, peak amplitude and decay time constant (when fitted with a single exponential) of the EPSC recorded at the soma, as well as the local voltage escape (in voltage clamp) for synaptic locations simulated successively in each dendritic compartment of Cell 1. Colour bars, 100 μm.

Figure 9. Attenuation of CF EPSCs.

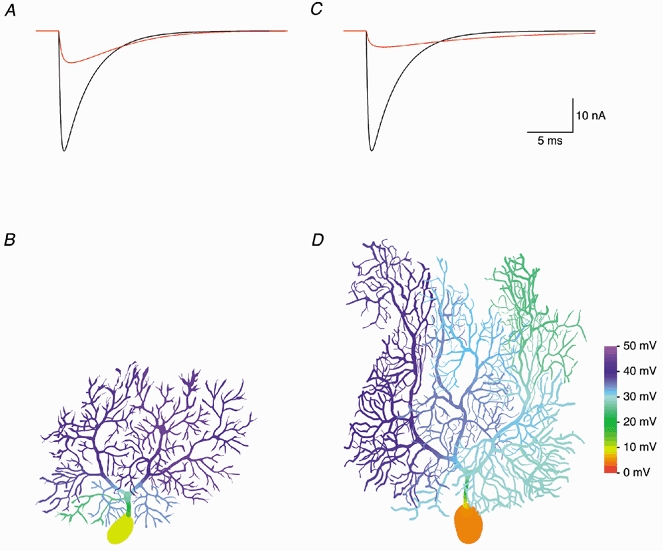
To simulate CF EPSCs, 500 quantal conductances were distributed along the main dendrites (grey region in Fig. 3A) at a constant density per dendritic length and activated synchronously. A, the CF EPSC recorded at the soma of the best-fit passive model of Cell 1 (red trace) is strongly attenuated compared to the EPSC expected under conditions of ideal clamp (black trace). B, colour-coded representation of peak dendritic depolarization during voltage clamp of the CF EPSC. C and D, same as A and B but simulated in the best-fit passive model of Cell 4. Colour bar, 100 μm.

To separate distortions of the somatic EPSC due to dendritic filtering from attenuation due to local voltage escape at the synapse, which reduces the driving force for the synaptic current, we first tested space-clamp for small synaptic conductances (peak, 1 nS), comparable to the conductances evoked by a single quantum of transmitter (Barbour, 1993; Silver et al. 1998). Somatic voltage clamp was unable to adequately control the dendritic voltage response (compare blue and green traces in Figs 7A and C and 8A and C) during a quantal synaptic conductance. However, the local voltage escape was usually small, in the range of 0.5-4 mV (except at some dendritic tips where it could reach 24 mV; see Fig. 7E and Fig. 8E, lower right panels). For excitatory synapses located on Purkinje cell spines, an additional voltage escape occurs due to the resistance of the spine neck. Assuming a spine neck resistance of 44 MΩ (Häusser et al. 1997) and a dendritic membrane potential ≥ -70 mV, this amounts to an additional depolarization of less than 3 mV for a 1 nS synaptic conductance with a reversal potential of 0 mV. Consequently, for most excitatory synapses the driving force changes by less than 10 % during a single quantal EPSC, despite the poor voltage control offered by somatic voltage clamp. Synaptic voltage escape is thus not a major problem when recording quantal PF EPSCs with a somatic electrode (although it can become a serious issue when many quanta are released; see below).

Figure 8. Attenuation of quantal EPSCs in a P21 Purkinje cell.

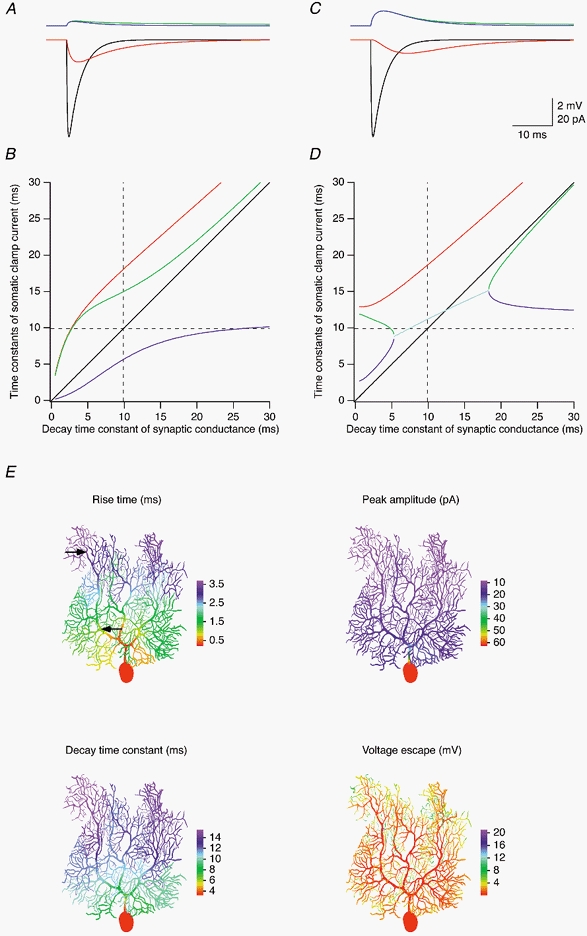
Same simulations as shown in Fig. 7, but performed with the best-fit passive model of Cell 4. See legend of Fig. 7 for details.

Dendritic filtering of the synaptic current, however, caused significant distortions of the EPSC waveform recorded at the soma. The rise was slowed, the peak was attenuated and delayed, and the decay was prolonged in a similar fashion both for a proximal synaptic location on the main dendrite (Fig. 7A) and a more distal location on a spiny branchlet (Fig. 7C; locations indicated by arrows in Fig. 7E, upper left panel). EPSCs simulated in the P21 cell (Fig. 8A and C) were distorted more strongly, as expected from the more elaborate dendritic morphology at this age.

The dependence of the measured somatic EPSC decay on the decay kinetics of the synaptic conductance is shown in Figs 7B and D and 8B and D (same synaptic locations as in Figs 7A and C and 8A and C, respectively). Somatic EPSCs were fitted either with a single exponential describing the decay phase, or with double exponential fits of both the rising and decaying phase. Decay time constants (red traces) determined using monoexponential fits of the decay phase of the somatic EPSC were systematic overestimates of the actual decay time constant of the synaptic conductance. Decay time constants of fast quantal conductances (1 ms; Häusser, 1994) were overestimated by a factor of ∼3 in Cell 1, and a factor of ∼5 and ∼13 for the two synaptic locations in Cell 4, respectively. The relative error in the estimate of the decay time constant was generally smaller for slower conductances, but the absolute error was still considerable; it even increased for fast to intermediate time constants at proximal synaptic locations (Fig. 7B and Fig. 8B). Decay time constants (green traces) determined using biexponential fits of both the rising and decay phases of somatic EPSC were better estimates of the decay time constants of the synaptic conductance. Here, significant absolute errors were indeed restricted to synaptic conductance time constants smaller than τ′₂ (dashed lines; 2.18 and 9.83 ms in Cell 1 and Cell 4, respectively), as predicted by the two-compartment model (Llano et al. 1991). Also in accordance with the two-compartment model, the rising time constants (blue traces) in the biexponential fits approximated τ′₂ for large values of the decay time constant of the synaptic conductance. However, for intermediate values of the decay time constant of the distal synaptic conductances (Fig. 7D and Fig. 8D) the values of the rising time constants in the biexponential fits first approached the values of the respective decay time constants, creating a region (cyan traces) where the values of the fitted rising and decay time constants were very similar. In this region, the somatic EPSC waveform is difficult to represent and to fit as a sum of two exponentials since the two exponentials of increasingly large amplitude and opposite sign nearly cancel each other out, leading to severe numerical problems when using conventional fitting algorithms (but not with DISCRETE). For larger synaptic decay time constants, the two time constants of the biexponential fit separated again such that the decay time constant approached the true decay time constant of the synaptic conductance from below, and the rising time constant moved towards τ′₂ (horizontal dashed lines in Fig. 7D and Fig. 8D) from above. Interestingly, the cyan traces cross the unity lines (black traces) close to the points where the synaptic conductance decay time constants are equal to τ′₂.

To investigate the dependence of somatic EPSC kinetics and amplitude on synaptic location, and to study the location dependence of the local voltage escape, we simulated EPSCs for synaptic conductances placed successively in each compartment of the models of Cell 1 (Fig. 7E) and Cell 4 (Fig. 8E). The colour-coded representations illustrate that the rise, peak and decay are increasingly distorted with distance from the soma. While the rise time for synapses located in the proximal main dendrite is still relatively fast, the decay time constants and especially the peak amplitude change very quickly upon leaving the soma and remain relatively constant throughout the dendritic tree. Thus, the 20-80 % rise time is not a reliable predictor of the quality of space-clamp in Purkinje cells as judged by the distortions in peak amplitude and decay time constant of the EPSC waveform recorded at the soma.

Space-clamp errors associated with somatic recording of CF EPSCs

While quantal synaptic conductances, especially those at proximal dendritic locations, cause little voltage escape in Purkinje cell dendrites (see above), this may no longer be true for large, multiquantal synaptic conductances such as those associated with CF activation. We therefore simulated somatic voltage clamp of CF EPSCs in the best-fit passive models of Cell 1 and Cell 4. While the rising phase of the somatic EPSCs (red traces in Fig. 9A and C) was relatively fast (20-80 % rise time, 0.36 and 0.42 ms in Cell 1 and Cell 4, respectively), the peak was severely attenuated to 26.5 % of the amplitude expected under conditions of ideal clamp in Cell 1, and to 13.4 % in Cell 4. In addition, the decay phase was prolonged (decay time constant, 5.20 ms in Cell 1 and 11.05 ms in Cell 4).

The severity of the space-clamp problem encountered when recording CF EPSCs was caused by a substantial drop in driving force at the synapse due to a large dendritic voltage escape (Fig. 9B and D), with the local voltage deviating by up to 45 mV from the resting potential of -70 mV. However, the local voltage escape (and thus the actual synaptic driving force) was not homogeneous. This creates an additional problem for quantal analysis of CF EPSCs, as the presence of a gradient in synaptic driving force within the CF region is likely to cause large inter-site (type II) quantal variance (see Discussion). Similar problems may arise when many PF synaptic contacts are activated simultaneously.

A model of the hyperpolarization-activated cation current I_h

The compartmental models described above were constructed based on experiments done in the presence of a blocker of I_h, which exerts a powerful influence on the subthreshold excitability of Purkinje cells. In order to re-incorporate this conductance, we constructed a biophysical model of I_h based on somatic voltage-clamp measurements from Purkinje cells. As described previously (Crepel & Penit-Soria, 1986), hyperpolarizing voltage commands from a holding potential at -50 mV triggered a slowly activating inward current (Fig. 10A) that was identified as I_h on the basis of its insensitivity to millimolar concentrations of 4-AP and TEA, and sensitivity to Cs⁺ and ZD 7288. The current had an apparent reversal potential of -34.4 ± 3.47 mV (n = 5) and a half-maximal activation voltage of -73.2 mV (Fig. 10B). The behaviour of the current could be reproduced by a simple Hodgkin-Huxley scheme with activation and deactivation described by single-exponential kinetics (Fig. 10B and C).

Figure 10. A model of I_h in Purkinje cells.

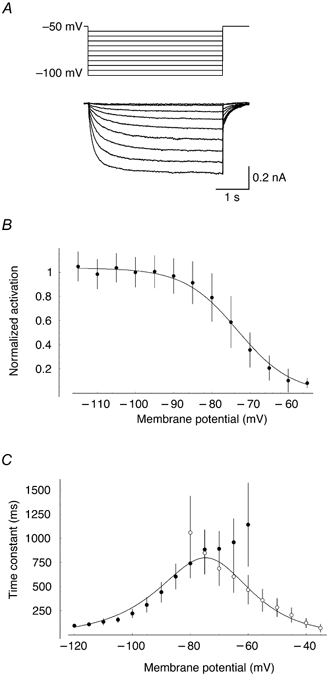
A, leak-subtracted traces of I_h activation in response to hyperpolarizing current steps from a holding potential of -50 mV. Somatic recording from a P12 Purkinje cell in the presence of TTX (1 μm), CdCl₂ (100 μm), 4-AP (1 mm), TEA (5 mm), CNQX (5 μm) and SR 95531 (30 μm). B, steady-state activation of I_h, normalized by driving force (unity at -100 mV; error bars, s.d.). The continuous line illustrates the prediction of the model of I_h (see Methods; a = 0.63 s⁻¹, b = 0.063 mV⁻¹, c = 0.079 mV⁻¹ and V_1/2= -73.2 mV). C, kinetics of I_h activation (•) and deactivation (○) at different command potentials. The corresponding curves from the model are superimposed.

In order to investigate the functional role of I_h, the model of I_h was inserted into the passive compartmental model of each neuron at a uniform density. Incorporation of I_h at a peak conductance density of 25 μS cm⁻², which reproduced the experimentally observed ‘sag’ waveforms in response to somatic current injection (Fig. 1A), did not significantly affect the kinetics of somatically recorded EPSCs in the model (not shown). However, the presence of I_h significantly affected the time course of EPSPs, as expected (Fig. 1A), and thus I_h was included in all simulations of EPSP attenuation.

Dendritic attenuation of EPSPs

The dependence of synaptic efficacy, as measured by the EPSP amplitude at the soma, on synaptic location was assessed in current-clamp simulations of quantal EPSPs in the best-fit models of Cell 1 and Cell 4 including I_h (Fig. 11 and Fig. 12). While the somatic EPSP waveforms (red traces) had similar amplitudes in each cell, and an approximately monoexponential decay for both proximal (Fig. 11A and Fig. 12A) and distal synaptic locations (Fig. 11B and Fig. 12B; locations indicated by arrows in Fig. 11C and Fig. 12C, upper left panels, respectively), local dendritic EPSPs (green traces) at distal locations had a larger amplitude than local EPSPs at more proximal locations, and a clearly biphasic decay. Thus, while the synaptic conductance is active, charge entering at the synaptic location is distributed across the cell, driven by the gradient between the local EPSP (green traces) and the membrane potential in the rest of the cell, for example at the soma (red traces). After termination of the synaptic current, this gradient dissipates and the membrane potential decays approximately homogeneously towards the resting potential.

Figure 11. Attenuation of quantal EPSPs in a P14 Purkinje cell.

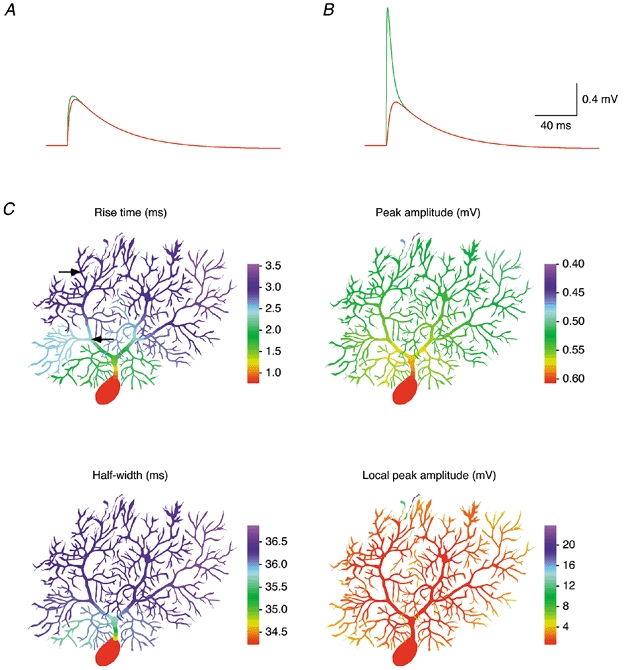
Synaptic potentials were simulated in a model of Cell 1 including I_h (see Methods). A, subsynaptic EPSP (green trace) and somatic EPSP (red trace) simulated for the synaptic location indicated by the proximal arrow in C. B, same as A but simulated for the synaptic location indicated by the distal arrow in C. C, colour-coded representation of the 20-80 % rise time, peak amplitude and half-width (full width at half-maximum) of the EPSP recorded at the soma, as well as the local EPSP amplitude for synaptic locations simulated successively in each dendritic compartment of Cell 1. Colour bars, 100 μm.

Figure 12. Attenuation of quantal EPSPs in a P21 Purkinje cell.

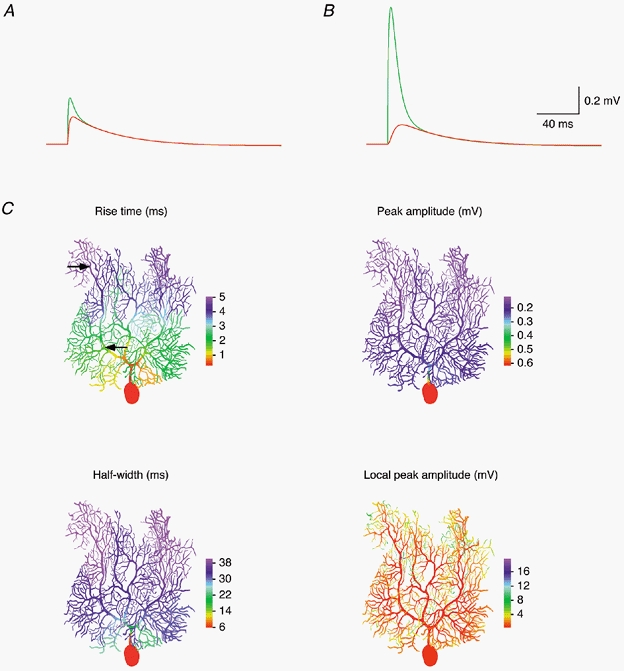
Same simulations as shown in Fig. 11, but performed with a model of Cell 4 (including I_h).

The dependence of the rise time, amplitude and half-width of somatic EPSPs on synaptic location and the location dependence of the local dendritic EPSP amplitude are illustrated in detail in Fig. 11C and Fig. 12C. Here we simulated EPSPs for quantal synaptic conductances placed successively in each compartment of the models of Cell 1 (Fig. 11C) and Cell 4 (Fig. 12C). The colour-coded representations illustrate that the 20-80 % rise times of somatic EPSPs increase substantially with distance of the synapse from the soma, from 0.76 to 3.54 ms in Cell 1 and from 0.29 to 5.05 ms in Cell 4. In contrast, the somatic EPSP amplitude was less dependent on synaptic location. For synapses on spiny branchlets, the somatic EPSP amplitude was 0.53 ± 0.02 mV (range, 0.46-0.58 mV) in Cell 1, and 0.17 ± 0.03 mV (range, 0.12-0.26 mV) in Cell 4. However, in Cell 4 the somatic EPSP amplitude increases dramatically as the synaptic location approaches the very proximal dendrites and the soma. Concomitantly, the somatic EPSP half-width decreases by a similar factor. A similar range of amplitudes and time courses was observed for simulated IPSPs (not shown). This indicates that, especially in older Purkinje cells, the somatic waveform of synaptic potentials of proximal origin may be shaped significantly by the charge redistribution within the cell while the synaptic conductance is active. Thus, synapses at or close to the soma are in a position to control the somatic membrane potential and influence Purkinje cell firing with high temporal precision.

DISCUSSION

We constructed detailed compartmental models of Purkinje cells in rat cerebellar slices. Passive cable properties were probed by simultaneous whole-cell recording of voltage responses to brief current pulses injected alternately at somatic and dendritic locations. Direct fits of the impulse responses, using models based on detailed morphological reconstructions of the same cells, provided sets of passive parameters that were little affected by statistical errors but suffered from significant systematic errors, especially due to uncertainties about dendritic diameters and spine densities. However, core model properties and predictions of the models, such as the quality of space-clamp during somatic recording of synaptic currents, were relatively insensitive to systematic errors since morphological errors were largely compensated by corresponding errors in the raw electrical parameters. Comparison of the detailed models with a two-compartment model of Purkinje cells showed that although a central assumption of the two-compartment model was violated for our Purkinje cells, its predictions of the range of synaptic current kinetics that can be faithfully space-clamped were still correct. Simulations of synaptic potentials in detailed compartmental models including a model of I_h indicated that individual synapses on spiny branchlets (assuming equal conductances) are nearly equally able to influence the somatic membrane potential, independent of their distance from the soma. However, especially in more mature neurons, synapses very close to or at the soma are in a privileged position to influence the somatic membrane potential in a temporally precise manner.

Construction of the model

Our passive compartmental models of Purkinje cells differ from two previous models of these neurons (Shelton, 1985; Rapp et al. 1994) in several respects. First, they are based not on microelectrode recordings, but rather on whole-cell patch-clamp recordings, which allow the possibility of a shunt conductance due to microelectrode impalement to be neglected (Major et al. 1994). Second, as the four neurons modelled exhibited a range of membrane time constants (τ_m; Table 3), we did not attempt to fit them as a group with identical parameters (Rapp et al. 1994), or combine electrophysiological and morphological data from different neurons (Shelton, 1985). Instead, we chose to construct individual compartmental models with individual passive parameters for each cell, based on its combined electrophysiological and morphological properties, to capture the inter-cell variability of both morphological and electrical parameters.

Finally, the most significant advance of the present model is that it is based on simultaneous somatic and dendritic recordings, which confers several advantages as outlined in the Introduction. In particular, when combined with brief current pulses as test stimuli (see below), multi-site recording allows direct measurements of the attenuation of transient changes in membrane potential. Compartmental models reproducing the measured voltage transients at the soma and a dendritic location in the reconstructed morphology can be expected to predict the attenuation of similar voltage transients, such as EPSPs, with high accuracy. Multi-site recording generally contributes more information about the electrotonic structure of a neuron than single-site recording, thus providing tougher constraints for the construction of compartmental models. Alternatively, compartmental models can be constructed using only a part of this information, while the remainder can then serve as a consistency check to validate the models.

The electrotonic structure of Purkinje cells was assessed using brief current pulses (Major et al. 1994; Rapp et al. 1994). This avoids the problems due to imperfect bridge balance that can affect measurements of steady-state attenuation (Stuart & Spruston, 1998) or frequency-domain analysis using sinewaves (e.g. Tabak et al. 2000), and minimizes changes in the activation state of slowly activating voltage-dependent conductances. Conditions for extracting passive parameters from impulse responses are particularly favourable in the P14-P21 Purkinje cells studied here. Voltage responses to somatic and dendritic current pulses were clearly biphasic, with a fast charge redistribution phase (whose amplitude and time course were very sensitive to the value of R_i), and a slow phase of homogeneous decay towards the resting membrane potential (Fig. 3). Since these two phases were temporally well separated, direct fits of the impulse responses converged easily, and the best-fit parameters were affected very little by recording noise (Table 3, statistical errors). In other cell types the situation may be less favourable. In hippocampal CA3 interneurons, for example, the amplitude of the charge redistribution transient is so small that R_i could not be determined from the data (Chitwood et al. 1999). In contrast, the long apical dendrite of layer 5 pyramidal cells causes charge redistribution transients with large amplitudes but relatively slow time courses (Stuart & Spruston, 1998), leading to poor temporal separation of the charge redistribution phase and the homogeneous decay phase. As a consequence, fit parameters are more difficult to identify uniquely, and may thus be affected more strongly by statistical errors due to recording noise. Similar effects are observed in cases where τ_m is relatively fast and therefore difficult to separate from the time constant of charge redistribution, for example in ventral horn neurons (Thurbon et al. 1998).

Best-fit passive parameters

The best-fit values for C_m of 0.77 ± 0.17 μF cm⁻² (Table 3) are in agreement with direct measurements of neuronal C_m by Gentet et al. (2000) and are consistent with the results of numerous passive modelling studies (Clements & Redman, 1989; Major et al. 1994; Chitwood et al. 1999). Several modelling studies have estimated C_m values considerably in excess of 1 μF cm⁻² (Stuart & Spruston, 1998; Thurbon et al. 1998), including one of Purkinje neurons (Rapp et al. 1994). In the latter study, the high estimate for C_m may be related to the lower spine density assumed in these models, to tradeoffs between the assumed high R_i and increase in C_m, or to the absence of the axon in the reconstruction.

The specific membrane resistance estimated for Purkinje cells (122 ± 18 kΩ cm²) is higher than that estimated for other neuronal types (Clements & Redman, 1989; Spruston et al. 1994; Stuart & Spruston, 1998; Thurbon et al. 1998), although is similar to the values found for CA3 pyramidal cells (120-200 kΩ cm²; Major et al. 1994). The relatively high value of R_m in these neurons points to a lower density of leak conductances compared to other neuronal types, and results in a relatively long membrane time constant for these neurons. The effective value of R_m, and of the membrane time constant, in the intact brain is likely to be lower and may depend on a variety of factors, including background synaptic activity (Häusser & Clark, 1997), ambient levels of neurotransmitters, modulation of leak channels and I_h, and on temperature, as τ_m varies with temperature in several cell types (e.g. Volgushev et al. 2000) and C_m is thought to be temperature insensitive.

The value of the intracellular resistivity (R_i) is usually the most difficult parameter to determine from this type of experiment (Major et al. 1994; Chitwood et al. 1999). It is constrained by relatively few data points at the beginning of the transient responses, and depends strongly on the accuracy of the morphological reconstruction, especially dendritic diameters (Major et al. 1994). Surprisingly, according to our error analysis our estimate of R_i is less affected by systematic errors (see below) than the values of C_m and R_m. The mean value obtained for R_i (115 ± 20 Ω cm) is smaller than the values reported for this parameter in several neuronal types (170-340 Ω cm; Shelton, 1985; Major et al. 1994; Rapp et al. 1994). It is comparable, however, to the range of values found recently using double whole-cell recording (68-151 Ω cm; Stuart & Spruston, 1998; 72-119 Ω cm, Thurbon et al. 1998), and to the estimate of Stämpfli & Hille (1976) for vertebrate axons (110 Ω cm), but is higher than that directly measured for squid axon (35.4 Ω cm; Hodgkin & Huxley, 1952), which is not surprising given that squid axoplasm has a very different ionic composition. Our value is consistent with the traditional value of 70 Ω cm (predicted from the conductivity of saline, assuming low mobility of the majority of anions) if tortuosity and volume exclusion due to the presence of organelles and the cytoskeleton in dendrites are taken into account.

Sources of error

There are several potential sources of error that may contribute to uncertainty in the model parameters. These can be separated into statistical and systematic errors, each of which we considered individually. From our error analysis we concluded that statistical errors (arising from recording noise and from the limited number of traces obtainable during an experiment) do not contribute significantly to errors in the model parameters. This is surprising (cf. Major et al. 1994) and suggests that substantially increasing the number of traces recorded will not significantly improve the model. Systematic errors, on the other hand, can seriously affect the specific values of the individual parameters. Fortunately, the effects of systematic errors on model predictions are relatively benign due to tradeoffs between the parameters, indicating that while individual model parameters may be inaccurate, the model still provides a faithful representation of the passive behaviour of the neuron.

Probably the most serious source of systematic errors is the morphological reconstruction. These errors may take several forms (Major et al. 1994; Jaeger, 2001). First, shrinkage and swelling during tissue processing may contribute to errors in length and diameter estimates. This was judged to be minimal (< 5 %) from comparison of diameters and lengths during the recording and after the processing procedure (see Methods). Second, the measurement of diameter itself may be subject to considerable error, particularly for the finest dendrites approaching the limits of resolution of the light microscope, and dendrites covered with spines. Variations in diameter during the error analysis revealed this to be an important contribution to systematic errors in the estimation of R_i (see also Major et al. 1994). Third, spine density is a critical parameter as spines comprise a large fraction of total membrane area in Purkinje cells. Our estimate of spine density is based on results from serial EM reconstruction of Purkinje cell spiny branchlets (Harris & Stevens, 1988; Napper & Harvey, 1988). Finally, while we took care to include the axon of each neuron in the reconstruction, the parameters of the axon may be somewhat uncertain due to its fine calibre and the presence of myelination, obscuring stretches of axon.

The recording conditions are also associated with several potential systematic errors. First, although great care was taken to ensure linear and passive behaviour of the neurons during the recording, the contribution of voltage-gated conductances cannot be entirely ruled out. Second, uncertainties about the exact position of dendritic recording pipettes may introduce systematic errors (Table 1) into the model when comparing measured and simulated dendritic voltage transients during the fit procedure. These were minimized by careful measurement of the electrode position during recording, aided by the high density of branch points in Purkinje cells, allowing us to uniquely identify the dendritic recording site by reference to details of the dendritic branching pattern during and after the recording. Third, due to their smaller size dendritic pipettes typically have large series resistances which may change during recording. Bridge balance was therefore monitored continuously, and sweeps were averaged in intervals during which series resistances were relatively stable. Realistic compartmental models of the pipettes were used during fitting, and the series resistances of the model pipettes matched the series resistances observed during experiment. Finally, pipette capacitance may be an appreciable fraction of total cell capacitance (Major et al. 1994). To minimize their capacitance, pipettes were coated with Sylgard, and optimal capacitance compensation was employed. Residual capacitance at the pipette tip, which is distributed in parallel with the series resistance and therefore cannot be fully compensated by the amplifier (Thurbon et al. 1998), was included as a free parameter during initial fits of impulse responses, and as a source of systematic errors in the error analysis (Table 1).

A final potential source of error which is very difficult to assess quantitatively is the structure of the model itself. We constructed our compartmental models with the simplest possible assumption, namely that the passive parameters are homogeneously distributed. While this assumption proved adequate to constrain our models within a reasonable margin of error, it is difficult in principle to rule out alternative models with more complex distributions of parameters. The lower value of somatic vs. dendritic R_m assumed in the model of Purkinje cells constructed by Rapp et al. (1994) is not necessarily inconsistent with our models since it could be due to a shunt conductance associated with somatic microelectrode recording. Although two-site recording can give an indication of inhomogeneities in the passive parameters, it cannot clearly distinguish between alternative inhomogeneous models, e.g. between an inhomogeneity in R_m (Stuart & Spruston, 1998; London et al. 1999) and an inhomogeneity in R_i. To exclude or confirm an inhomogeneous distribution of R_i in dendrites, simultaneous recording from at least three sites would be required (Kleinle, 1998). We conclude that future refinements of passive models of neurons will depend primarily on improved acquisition of morphological data, for example by combining high-resolution confocal microscopy, deconvolution, and novel image processing techniques allowing automated reconstruction of neuronal morphology, as well as on multi-site recordings.

Reduced models of Purkinje cells

The two-compartment model of Purkinje cells described by Llano et al. (1991) is easier to construct than the detailed models presented here, and its predictions can be calculated analytically. On the other hand, it represents a considerable simplification and is based on certain assumptions that need to be tested. The basic assumption of the two-compartment model is that the capacitive current recorded at the soma in response to a somatic voltage-clamp step can be fitted by a sum of two exponentials. While this assumption does not hold statistically when tested for our detailed compartmental models and assuming typical levels of recording noise, it is nevertheless a good approximation since the amplitudes of the additional exponentials are relatively small (Fig. 5B and D, insets). The two-compartment model correctly predicts the range of decay time courses of synaptic currents that can be faithfully recorded at the soma of Purkinje cells, which is its original purpose (Llano et al. 1991). Unfortunately, as the assumption of double-exponential somatic capacitive currents is already violated in Purkinje cells, this cannot be used as a criterion to decide whether the two-compartment model is applicable to a given cell type, or whether a multicompartmental model or a cable analysis (Jackson, 1992) is required. Clearly a two-compartmental model also cannot correctly predict the location dependence of steady-state (Fig. 4) and transient attenuation (Fig. 6). In particular, the distal compartment, in which the voltage response to a somatic voltage-clamp step is monoexponential, is not represented by all spiny branchlets (as proposed by Llano et al. 1991), but by a horizontal band representing the distal CF region and the corresponding intermediate PF region (Fig. 6, regions shown in grey).

Analysis of the two-compartment model highlights the importance of fitting experimentally recorded PSC waveforms with the correct number of exponentials (see also Llano et al. 1991). For example, fitting slowly rising EPSCs of dendritic origin with a single decaying exponential can overestimate the actual decay time constant by > 30 % since the rising phase can lead to a broadening of the peak region. Two- or three-exponential fits should therefore be routinely applied when the EPSC rise time is significant (Barbour, 1993). This fitting should be applied with care, as numerical difficulties can be encountered in conventional fitting algorithms when the time constants of the rising and decaying exponentials are similar.

Space-clamp errors in experimental studies of synaptic currents

Our modelling results demonstrate that even though Purkinje cells are compact under steady-state conditions, rapid transients such as synaptic currents recorded in voltage clamp can suffer from substantial filtering. As expected (Johnston & Brown, 1983; Rall & Segev, 1985; Major, 1993), this filtering is frequency dependent, with faster synaptic currents being affected more than slower currents. The degree of filtering also depends on the location of the synaptic input. While the somatic 20-80 % rise time increases rather continuously with distance of the input from the soma, the somatic EPSC amplitude drops abruptly for very proximal inputs and then stays nearly uniformly low across all spiny branchlets. This pattern is reflected in the dependence of somatic EPSP shape on input location (see below).

Our findings have important implications for experimental investigations of synaptic transmission in Purkinje cells using somatic voltage-clamp recordings. In mature Purkinje cells, even relatively slow PF synaptic currents cannot be accurately recorded via a somatic patch-clamp electrode, and fast synaptic currents are substantially distorted in both their kinetics and amplitude. Selecting somatic EPSCs based on the fastest 20-80 % rise times will not prevent the inclusion of EPSCs whose amplitude is severely attenuated. Note also that it will be difficult to discriminate CF and PF miniature EPSCs on the basis of rise time: although somatic and primary trunk contacts will contribute the very fastest-rising EPSCs, there is substantial overlap in rise time between EPSCs originating in the distal CF region, and those originating at proximal spiny branchlets (compare the CF region illustrated in Fig. 3A, and the distribution of rise times shown in Fig. 8E).

These space-clamp problems can be circumvented in several ways. First, their severity increases with the age of the Purkinje cell recorded from. Recording EPSCs in younger (less than P10) Purkinje cells should therefore alleviate the problem. Second, EPSCs can be recorded directly from the dendrites of Purkinje cells (Häusser, 1994), to minimize the distance from active synapses. Third, the true time course of the synaptic current can be reconstructed using somatic voltage jumps timed to occur at various intervals with respect to the onset of the synaptic conductance (Häusser & Roth, 1997). Finally, synaptic currents can be classified as well clamped (Llano et al. 1991) and even back-calculated using a compartmental model (e.g. Nadeau & Lester, 2000). Best results are expected when the voltage jump method is combined with calculations in a compartmental model of the cell recorded from (Häusser & Roth, 1997).

An additional complication arises when recording EPSCs resulting from simultaneous activation of many synaptic contacts, e.g. during compound PF and particularly during CF stimulation. Under physiological conditions, the CF synaptic conductance is very large and causes substantial voltage escape (Fig. 9B and D), which adds to the distortion of the somatic EPSC waveform by reducing synaptic driving force in a time-dependent manner. In addition, the voltage escape is spatially non-uniform (Llinás & Nicholson, 1976), and thus creates an additional component of inter-site (type II) quantal variance which must be considered when performing quantal analysis of CF synaptic currents (Silver et al. 1998). This effect may be further complicated by activation of dendritic voltage-gated conductances.

Functional architecture of the Purkinje cell dendritic tree

The Purkinje cell has one of the most remarkable dendritic trees of any neuronal type in the central nervous system. Its basic features are conserved across a wide range of species and throughout evolution. Functionally, its passive architecture is able to perform tasks which at first sight seem hard to reconcile. In the somatofugal direction, the thick, short main dendrites allow steady-state potentials to be distributed effectively (Fig. 4A), resulting in good steady-state voltage control of the dendrites from the soma, in agreement with direct patch-clamp (Stuart & Häusser, 1994) and voltage-sensitive dye measurements (Staub et al. 1994; Borst et al. 1997). On the other hand, fast transients travelling in the same direction, such as backpropagating action potentials, are extremely attenuated due to the high branching density and the resulting large cumulative impedance mismatch (Rall, 1964; Stuart & Häusser, 1994; Vetter et al. 2001). EPSPs spreading in the somatopetal direction are equalized in such a way that increased voltage attenuation from distal locations to the soma is nearly compensated by increased local amplitude at their site of generation, due to the larger local input impedance. Thus, in contrast to neocortical and CA1 pyramidal cells, where greater than 10-fold differences in efficacy are predicted for synapses at different locations (Stuart & Spruston, 1998; Magee & Cook, 2000; Berger et al. 2001), somatic EPSP amplitude is only weakly dependent on synaptic location on Purkinje cell spiny branchlets (Fig. 11 and Fig. 12). This ‘dendritic democracy’ is already achieved by the passive structure of Purkinje cells and is due to the absence of a long primary dendrite (Jaffe & Carnevale, 1999). Under in vivo conditions, the attenuation of synaptic potentials in the Purkinje cell dendritic tree may be increased due to background synaptic input, thus enhancing the location dependence of synapses. Under these conditions, active boosting of distal EPSPs may be required to normalize EPSP amplitude at the soma (De Schutter & Bower, 1994).

Finally, fast regenerative events originating in the dendrites face similar impedance mismatches as backpropagating action potentials and are thus kept much more localized than in other cell types (Vetter et al. 2001). Thus, the passive dendritic architecture of Purkinje cells may be optimized to accommodate multiple sites of synaptic integration, theoretically leading to a significant enhancement of their computational power (Mel, 1993; Poirazi & Mel, 2001). Active compartmental models (De Schutter & Bower, 1994) based on realistic passive parameters will be required to study the interactions of synaptic potentials, action potentials and dendritic spikes during network activity in vivo.

Supplementary material

The online version of this paper (http://jphysiol.org/cgi/content/full/535/2/445) contains supplementary material entitled ‘Estimation of statistical errors using the bootstrap method: Balanced resampling of sweeps’.