GABA-induced current and circadian regulation of chloride in neurones of the rat suprachiasmatic nucleus

Abstract

1. We have shown previously that GABA, the main neurotransmitter in the suprachiasmatic nucleus (SCN), has dual effects on SCN neurones, excitatory during the day and inhibitory at night. This duality has been attributed to changes in [Cl⁻] _i during the circadian cycle. To unravel the processes underlying these changes we investigated the biophysical properties of the GABAergic receptors and the regulation of [Cl⁻] _i in SCN neurones.

2. We used voltage-clamp methodology in conjunction with local application of GABA to characterise the current induced by GABA in SCN neurones within acute brain slices. This current, mediated via GABA_A receptors, shows moderate voltage dependence, does not desensitise and can significantly alter [Cl⁻] _i.

3. Loading or depletion of intracellular Cl⁻ was induced by a train of GABA pulses. The recovery of intracellular Cl⁻ was deduced from the change in [Cl⁻] _i calculated from the response to a test GABA pulse presented at different intervals after the conditioning train of GABA application. The time course of recovery was described by an exponential curve. Recovery following Cl⁻ depletion was slower than recovery from Cl⁻ loading and was further delayed during the subjective night.

4. We concluded that: (a) SCN neurones express a large number of somatic GABA_A receptors, which give rise to a modifiable, tonic Cl⁻ conductance that modulates cell excitability; (b) two Cl⁻ transport mechanisms operate in SCN neurones, one that replenishes the cell with Cl⁻ following Cl⁻ depletion and another that removes Cl⁻ after Cl⁻ loading; (c) the efficiency of the replenishing mechanism is reduced during the subjective night; and (d) this reduction explains a lower [Cl⁻] _i during the night phase of the circadian cycle.

There is hardly a facet of mammalian physiology and behaviour that is not subject to diurnal variation and control, from sleep/wakefulness and endocrine function to thermoregulation and metabolism. The best-defined master oscillator that orchestrates these myriad functions is the brain's circadian clock, which resides in the hypothalamic suprachiasmatic nucleus (SCN). In the last few years, substantial progress has been made in understanding the molecular basis of the circadian clock (Young, 2000) that probably exists in most SCN neurones (Welsh et al. 1995). However, it is not yet known how this molecular clock produces circadian alteration of any physiological parameter and even the mechanism for synchronisation between SCN neurones (Liu et al. 1997) is still a mystery.

Most SCN neurones contain GABA and show GABAergic synaptic activity, mediated mainly by GABA_A receptors (Kim & Dudek, 1992; Gao & Moore, 1996; Wagner et al. 1997). A large body of data, accumulated over the last few years, indicates that GABA plays a prominent role in regulating the circadian oscillations in firing rates (Tominaga et al. 1994; Gillespie et al. 1997). It is not surprising, therefore, that both GABA_A and GABA_B receptors have been identified in the SCN (Kim & Dudek, 1992; Gao et al. 1995; Jiang et al. 1995; O'Hara et al. 1995). It is well established that the metabotropic GABA_B receptor acts by closing calcium and opening potassium channels (Bormann, 1988), whereas GABA_A receptors conduct mainly chloride ions (Sivilotti & Nistri, 1991; Kaila, 1994). GABA_A-mediated currents rise quickly with a time constant of the order of milliseconds and desensitise with a time constant of about 1-20 s during long-lasting agonist applications (Mierlak & Farb, 1988; Tauck et al. 1988). Fast agonist application techniques revealed another desensitisation process, occurring over a time range of tens of milliseconds (Jones & Westbrook, 1995). Although the main action of GABA is inhibition, excitatory responses to GABA have been encountered in several cases and these were mediated either by maintenance of a high intracellular chloride concentration or by a relatively small but effective bicarbonate conductance of the GABA_A receptor (for a review see Kaila, 1994).

We have demonstrated (Wagner et al. 1997) that GABA, via GABA_A receptors, increases the firing rate of SCN neurones during the day and decreases it during the night. Although this observation has been contested by recent work (Gribkoff et al. 1999), it is still fully reproducible in our laboratory and has been further confirmed by non-invasive optical measurements (Chorev et al. 1997; see also Shirakawa et al. 2000; Colwell, 2001). Several lines of evidence led us to conclude that these dual effects of GABA are probably due to circadian changes in intracellular chloride concentration, from high levels during subjective day to low levels during subjective night. Such a change in intracellular chloride concentration can be generated either by a change in passive chloride fluxes or by changes in the efficiency of active chloride regulating mechanisms.

Chloride regulation is usually attained by a secondary transport system, where the translocation of an ion is coupled to the translocation of another ion in the same (cotransport) or the opposite (countertransport) direction. A variety of chloride transport systems have been described in vertebrate nerve cells, including inwardly as well as outwardly directed transporters coupled to sodium, potassium or certain amino acids (Dehnes et al. 1998; Chang & Lam, 1998; Staley & Proctor, 1999; Vu et al. 2000; Kakazu et al. 2000; Kawamoto et al. 2001). It is interesting to note that SCN neurones are known to express amino acid uptake mechanisms, including the GABA (F. Nuernberger, personal communication), the serotonin (Amir et al. 1998) and the glutamate transporters (Cagampang et al. 1996; Ebling, 1996).

In this study, we characterised the GABA-induced current elicited by local and bath GABA applications in SCN neurones in acute hypothalamic slices. We found that the GABA-induced current in SCN neurones, which is mediated via GABA_A receptors, can significantly alter the intracellular chloride concentration. Furthermore, by either the loading or depletion of intracellular chloride and following the recovery process that restores the chloride concentration, we discovered that the chloride-regulating mechanism undergoes circadian changes that might explain the dual effects of GABA in the SCN.

METHODS

Animals

Young Sabra rats (2-4 weeks) were used for slice preparation. The animals were maintained in cages with food and water available ad libitum under a 12:12 light/dark cycle, with the light on at 07.00 h, for at least 2 weeks prior to dissection. All procedures used in the study adhered to guidelines approved by the Hebrew University of Jerusalem Animal Care Committee and conform to NIH guidelines.

Slice preparation

The rats were anaesthetised with pentobarbitone (60 mg kg⁻¹, i.p.) and heart perfused with aerated (95 % O₂-5 % CO₂) ice-cold physiological solution. Unless otherwise stated, the solution was composed of (mm): 120 NaCl, 5 KCl, 1.3 MgSO₄, 1.2 KH₂PO₄, 26 NaHCO₃, 20 glucose and 2.4 CaCl₂, pH 7.3. After decapitation, the brain was removed and a hypothalamic block was sliced into coronal sections of 300 μm thickness. The slices containing the SCN were pre-incubated in physiological solution at room temperature for at least 1 h prior to recording. Slices were prepared at Zeitgeber time (ZT) 2-4 (08.00-10.00 h) and ZT 12-14 (19.00-21.00 h) for day and night experiments, respectively.

Recordings

Slices were transferred to a recording chamber and perfused with aerated physiological solution at room temperature (unless otherwise stated). Recordings were made using the whole-cell patch technique in the voltage-clamp mode using an Axopatch-1D amplifier (Axon Instruments). For GABA-induced current characterisation experiments, patch pipettes were filled with a solution containing (mm): 120 potassium gluconate, 14 NaCl, 10 sodium gluconate, 0.5 CaCl₂, 5 Mg-ATP, 5 EGTA, 10 Hepes, pH 7.2 with a DC resistance of 10-15 MΩ. The chloride concentration was varied between 1 mm and 15 mm by replacing the NaCl with sodium gluconate. Experiments were performed in the presence of 0.1 μm TTX. For experiments describing chloride regulation, the pipette solution was composed of (mm): 140 sodium gluconate, 4 NaCl, 0.5 CaCl₂, 5 EGTA, 3 Mg-ATP and 10 Hepes. The inhibitors furosamide (frusemide, 1 mm), bumetanide (100 μm), bicuculline (20-100 μm) and acetazolamide (50 μm) were purchased from Sigma and added to the physiological solution. SCN cells were readily identified using infrared light and Nomarski optics (Axioscop, Zeiss). Recordings were made during ZT 4-9 (day animals) and during ZT 17-22 (night animals). Characterisation of the GABA-induced current was performed only during ZT 4-9 (day animals).

Experimental procedure

For bath application experiments, GABA was added to the physiological solution to a final concentration of 100-200 μm. For local application experiments, GABA was diluted to 1 mm (or 100 μm where stated) in physiological solution (pH 7.6) and applied locally from a patch pipette using pressure injection. The injection pipette was located 20-40 μm from the cell body.

In experiments exploring chloride regulation, membrane potential was held either above or below the GABA reversal potential, to allow the generation of symmetrical responses. A change in the intracellular chloride concentration was induced by a conditioning train of GABA pulses (five pulses of 500 ms duration, interpulse interval 700 ms). Recovery of [Cl⁻] _i was characterised using a 500 ms test pulse given at different times (8-35 s) after the train. Each trial included one conditioning train followed by a single test pulse. The holding potential was alternated between hyperpolarising and depolarising levels in successive trials, ensuring identical initial conditions for each trial.

Calculations

Glossary

V: membrane potential. I_GABA, g_GABA, V_GABA: GABA-induced current, conductance and the reversal potential of GABA, respectively. I_Cl, V_e,Cl, g_Cl: chloride current, equilibrium potential and conductance, respectively. I_HCO3, V_e,HCO3, g_HCO3: bicarbonate current, equilibrium potential and conductance, respectively.

The relative chloride conductance

In calculating the relative contribution of chloride to the GABA-induced conductance, we assumed that:

(1)

and

Thus:

(2)

Where

(3)

and

(Kaila et al. 1993; Staley & Proctor, 1999).

At the GABA reversal potential (where V = V_GABA):

(4)

and therefore:

or:

When the reversal potential is plotted as a function of log[Cl⁻] _o, the slope is equal to:

and the relative chloride conductance can be calculated.

The relative chloride current

Once the relative conductances are determined, chloride equilibrium potential can be calculated from eqn (4). The relative chloride current at each membrane potential is:

(5)

The change in chloride concentration

In order to calculate the amount of chloride loaded or depleted from the cell during a pulse of GABA, the integral of the response, which is the total charge transferred during the response (Q_GABA), was measured from the beginning of the pulse to the return of the current to its resting level (Fig. 1, grey area). To calculate the relative charge carried by chloride at a certain membrane potential we multiplied the total charge by the relative chloride current:

(6)

The change in chloride concentration was then extracted according to eqn (7):

(7)

where Δ[Cl⁻] _i is the change in intracellular chloride concentration, e is the charge of a chloride ion, N_A is Avogadro's number and vol is the cell volume, assuming a spheroid cell with an 8 μm diameter (van den Pol, 1980).

Figure 1. The parameters used to calculate intracellular chloride concentration.

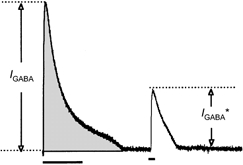
The integral of the response to the conditioning train (grey area) was used to calculate the amount of chloride loaded into or depleted from the cell. I_GABA, amplitude of current response to conditioning pulse; I_GABA^*, amplitude of current response to test pulse.

The recovery of chloride concentration

The amplitude of the response to the conditioning pulse, I_GABA (see Fig. 1), is given by eqn (1). Accordingly, the amplitude of the response to the test pulse, I_GABA^* (Fig. 1), is:

where V_GABA^* is the GABA reversal potential at the onset of the test pulse. Since the conductance, g, is equal for both responses, it follows that:

(8)

Using eqn (4) we calculated the actual change in chloride equilibrium potential and the corresponding change in intracellular chloride concentration (V_GABA was calculated from the amplitudes of the responses to the conditioning train at two different holding potentials).

Fitting exponential time course

The ratio, R, between the amplitude of the response to the test pulse, I*, and the amplitude of the response to the conditioning train, I, was used to calculate the time constant of the recovery process. An exponential curve was fitted to the experimental observations according to the equation:

where A = R_t - R_{t= 0} and t is the time at which the test pulse was applied, with t = 0 being the time of the first test pulse (8 s). Ā and τ, the maximum recovery and the time constant of the recovery process, respectively, were extracted from the curve that best fitted the results.

To fit an exponential time course to the recovery of the intracellular chloride concentration, C, the following equation was used:

where C =|C_t - C_{t= 35}| and t is the time at which the test pulse was applied, with t = 0 being the time of the first test pulse (8 s). As before, ⁻C and τ, the maximum change in chloride concentration and the time constant of the recovery process, respectively, were extracted from the curve that best fitted the results.

Data analysis

Electrical signals were stored on videotapes using a Neuro-corder (DR-484, Neurodata, NY, USA) and analysed by software written on the LabVIEW 5.01 data acquisition and programming system (National Instruments, TX, USA). One- and two-tailed Student's paired and unpaired t tests were made using Excel 5.0 (Microsoft).

RESULTS

Conductance change and reversal potential of the GABA-induced current

The response to local application of 1 mm GABA was studied under voltage-clamp conditions. When a holding potential of -40 mV, 1 mm of chloride in the patch pipette ([Cl⁻] _p= 1 mm) and 200 ms of GABA application were used, an outward current appeared after a delay of 74 ± 27 ms (n = 9) and reached an average amplitude of 358 ± 164 pA, with a rise time of 153 ± 39 ms. The total charge (see Methods) that crossed the membrane during this response was 295 ± 143 pC.

Figure 2A shows GABA-induced currents elicited from various membrane potentials, using 1 mm chloride in the patch pipette. As would be expected, inward currents were recorded when the membrane was hyperpolarised and outward currents were recorded when it was depolarised. The amplitude of the current response as a function of the holding potential is plotted in Fig. 2B. The peak amplitude of the current was linearly related to the membrane potential within the range -30 to -70 mV, yielding a peak conductance of 11.4 nS. The average value of 12.3 ± 4.5 nS (range 5-23 nS; n = 36) was about 20 times larger than the resting conductance of SCN neurones (0.6 ± 0.4 nS, n = 21, data not shown) and was independent of the chloride concentration in the patch pipette (Fig. 2C). The distinct linear relation observed below -70 mV suggests a second conductance state with a smaller value (7.9 nS). This hyperpolarisation-associated conductance state was observed in 26 of 35 neurones (74 %), and on average was 38 % smaller than the first state (n = 26), with no dependence on the chloride concentration in the patch pipette (P > 0.3).

Figure 2. The GABA-induced current is carried by chloride and bicarbonate ions and mediated via GABA_A receptors.

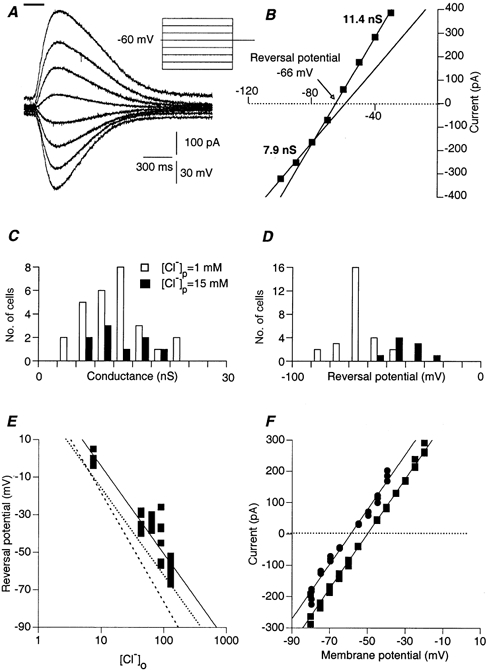
A, currents induced by 200 ms of local application of GABA (top bar). The currents were measured during 4 s-long voltage steps of various amplitudes. The concentration of chloride in the patch pipette was 1 mm. Note that the response elicited during the most depolarized voltage step is superimposed on a significant outward current. B, current-voltage relationships of the peak current responses shown in A. Two different linear relationships, which were found at two different voltage ranges (-30 to -70 mV and -80 to -100 mV), revealed two distinct conductance states. The values of the two conductance states were derived from the slopes of the linear regressions at the two voltage ranges. The reversal potential of the response was interpolated from the membrane potential where the current is zeroed (arrow). C, the distribution of the peak conductance measured in 27 neurones with 1 mm chloride in the patch pipette (open columns) and 9 neurones where 15 mm of chloride was used (filled columns). Mean values of 12.4 ± 4.6 nS and 12.2 ± 4.2 nS, respectively, were calculated (P > 0.4). D, the distribution of the reversal potential, measured as described for C. E, GABA reversal potential plotted as a function of the extracellular chloride concentration. Each data point represents a different neurone. Experimental results (▪) were fitted by a linear curve (continuous line) on a logarithmic scale. Dashed line, the expected relationship if chloride were the only charge carrier. Dotted line, the expected relationship when 81.5 % of the current was carried by chloride and 18.5 % by bicarbonate. Reversal potential of bicarbonate was taken to be -10 mV. Chloride concentration in the patch pipette was 5 mm. F, current-voltage relationships measured before (▪) and after (•) acetazolamide (50 μm) application.

In contrast to the peak conductance, the reversal potential of the GABA-induced current, measured as the potential of zero current (arrow in Fig. 2B), depended on the chloride concentration of the patch pipette solution. The results are summarised in Fig. 2D. Average reversal potentials of -65 ± 9 mV (open columns) and -40 ± 7 mV (filled columns) were calculated for 1 mm (n = 27) and 15 mm (n = 9) chloride, respectively (P < 5× 10⁻⁷). This dependence suggests that the GABA-induced current was mediated via GABA_A receptors. This was confirmed by adding bicuculline (100 μm) to the bath solution. Bicuculline completely and reversibly blocked the GABA-induced current in all experiments (n = 3, data not shown but see Fig. 5A). However, the 15 mV difference in the reversal potential was smaller than would be expected from a 15-fold change in chloride concentration, were chloride the only charge carrier. Thus, either other ions were involved in the GABA-induced current or the chloride concentration in the patch pipette was different from the chloride concentration in the recorded cell.

Figure 5. The response to bath application of GABA has the same properties as the response to local application.

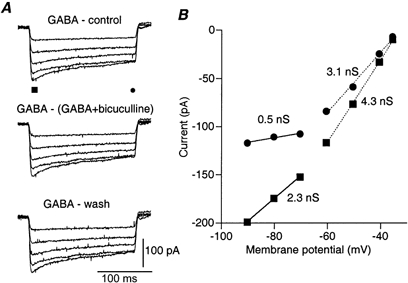
A, net current responses to voltage steps induced by bath application of GABA. The traces are the result of subtracting the currents measured before GABA application (top panel), after washing out GABA (bottom panel) or in the presence of both 100 μm GABA and 40 μm bicuculline (middle panel) from the currents measured in the presence of 100 μm GABA. Note the time dependence of the decay of the response and its voltage dependence. The chloride concentration within the patch pipette was 15 mm and the reversal potential was -45 mV. B, current-voltage relationships measured at the peak (▪) and the end (•) of the current responses. The values of the apparent conductances derived from the slopes of the linear current-voltage relationships are given on the figure.

To examine this point we measured the reversal potentials of the GABA-induced currents when the extracellular chloride concentration was varied from 7 to 127 mm (by replacing NaCl with sodium methanesulfonate, [Cl⁻] _p= 5 mm). The results are summarised in Fig. 2E. The calculated slope of -42 mV/log[Cl⁻] _o (continuous line) was significantly lower than the expected -58 mV/log[Cl⁻] _o (dashed line), suggesting that other ions participated in the response. Since the involvement of bicarbonate has been suggested (Kaila, 1994), we calculated the expected relationship assuming that the reversal potential for bicarbonate was -10 mV (see Methods). A slope of -42 mV/log[Cl⁻] _o was achieved, if we assumed that 18.5 % of the conductance was due to bicarbonate current (dotted line in Fig. 2E). The negative displacement (by 12 mV) of the calculated curve is probably due to the well-known phenomenon of junction potential between the patch pipette solution and the extracellular medium, caused by gluconate ions and estimated to be around 10 mV (Ng & Barry, 1995). This result strongly suggests that, as in other GABAergic synapses, bicarbonate carries some of the current. To confirm this possibility we measured the GABA-induced current in the presence of acetazolamide, a known blocker of carbonic anhydrase, the enzyme that ensures a constant level of intracellular bicarbonate (Supuran et al. 2000). As shown in Fig. 2F, the current-voltage relationships were shifted toward more negative values, as expected from a decrease in intracellular bicarbonate concentration (similar results were obtained in 4 more neurones).

The time course of the GABA-induced current

The time course of the GABA-induced current was studied by analysing the responses to GABA application of various durations. The three superimposed traces in Fig. 3A show the currents induced by 100, 500 and 1000 ms GABA applications. Increasing the duration of application significantly prolonged the response but had only a minor effect on the amplitude and no effect on the rise time. While the insensitivity of the rise time was to be expected, the independence of the amplitude and the duration of application (P > 0.5, ANOVA) indicated that saturating conditions were reached with 1 mm GABA application.

Figure 3. The change in GABA reversal potential during GABA-induced current.

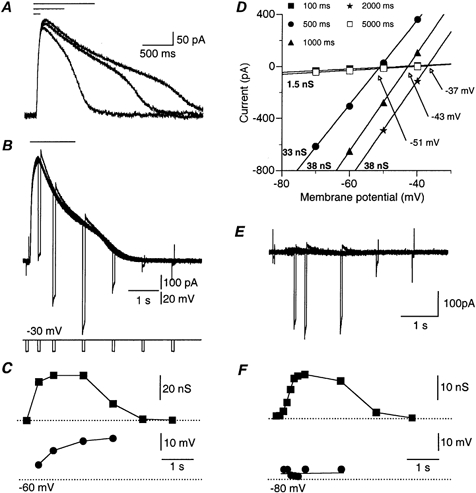
A, 3 superimposed current responses to 100, 500 and 1000 ms local GABA application (top bars) at -30 mV holding potential. Note that the response starts to decline in the presence of GABA. The second phase of the decay probably represents removal of GABA from the cell area. B, 7 superimposed traces of current responses to identical 1500 ms GABA applications (top bar), at a holding potential of -30 mV. Short (50 ms) voltage steps (-20 mV) were given at 0.1, 0.5, 1, 2, 3, 4 and 5 s after GABA application (see voltage traces below). Note the similarity of the amplitudes of the responses to the short voltage steps during the first phase of decay of the GABA-induced current. Note also the tail currents at the end of the short voltage steps and that the current decreases during the pulses. Both reflect a change in driving force during the voltage steps. C, conductance (▪) and reversal potential (•) plotted as a function of time. Dotted line at the bottom denotes a -60 mV value. D, current-voltage relationships measured during the short voltage steps shown in B. The conductance values derived from the slope of these linear relationships is marked at the bottom of each curve. Note that the conductance at the peak of the response (33 nS) is smaller than that calculated at 1000 ms (38 nS). The intersections of the curves with the control curve (arrows) denote the reversal potential of GABA at each time point. E and F, as in B and C, but in a different cell where the membrane potential was clamped at the reversal potential of GABA (-75 mV). Note that the reversal potential in F was unaffected by the GABA application.

At longer durations, the currents started to decline long before the termination of the GABA applications, resulting in a distinctive peak (Fig. 3A and B). This might have been due to a time-dependent reduction in either the conductance or the driving force. To distinguish between these possibilities we calculated the time course of the conductance change during the GABA-induced current. Short voltage steps (50 ms) of different magnitude were applied before, during and after 1500 ms of GABA application (Fig. 3B). The current-voltage relationships were plotted at each time point (Fig. 3D). The conductance and the reversal potential for each time point were calculated from the slope of the current-voltage relationships (Fig. 3D, bold numbers) and the intersections of the curves (Fig. 3D, arrows), respectively. The comparison of the time course of the conductance change (Fig. 3C, ▪) with that of the GABA-induced current (Fig. 3B) revealed that the early decline of the current is not due to conductance decrease. While the current peaks at 500 ms and is decreased by 30 % at 1 s, the conductance at 1 s is larger than that calculated at 500 ms. Similar results were observed in all 23 neurones tested this way. Thus, it seems clear that the decline of the response during the application was not due to desensitisation but most probably resulted from a decrease in the driving force. This was confirmed by plotting the calculated reversal potential as a function of time (Fig. 3C, •). The reversal potential shifted continuously and monotonically as long as GABA was present and the conductance was high.

The shift in the reversal potential might have been due either to local changes within the cell, such as chloride accumulation within the cytoplasm, or to alterations in the extracellular milieu, due to responses of many cells adjacent to the application area. In order to distinguish between these two possibilities, we similarly examined the dynamics of the reversal potential when the cell was clamped to the original reversal potential of GABA (Fig. 3E). Figure 3F demonstrates that under these conditions, when no current was elicited by the GABA application, a sigmoidal conductance increase was still evident (▪), but the reversal potential maintained a constant value of about -73 mV (•). This result suggests that the dynamics of the reversal potential during local GABA application are governed by chloride ions entering the neurone through GABA_A channels.

Mechanisms underlying the change in reversal potential

Is the influx or efflux of chloride ions during the response to local GABA application sufficient to explain the change in the intracellular chloride concentration and, hence, the change in the reversal potential of the GABA response?

Theoretical considerations, using eqn (7), show that 1 mm change in the free chloride concentration would require a chloride charge transfer of 27 pC. The mean charge transferred across the membrane of SCN neurones clamped to -40 mV during a response to 200 ms local GABA application was 295 pC (see above). However, due to the participation of HCO₃⁻, the actual chloride charge was 350 pC (see eqn (6)). Thus, a 13 mm change in the intracellular chloride concentration would be expected. As [Cl⁻] _i within neurones is estimated to be 3-20 mm (Ebihara et al. 1995), a 13 mm change can dramatically alter the reversal potential of GABA.

The effect of the GABA-induced current on intracellular chloride concentration was examined experimentally by measuring the response to GABA application following a conditioning, GABA-induced current. The membrane potential was clamped to the GABA reversal potential (-45 mV, [Cl⁻] _p= 15 mm) and two GABA applications of 500 ms separated by 2.5 s were given. As shown in Fig. 4A (top trace), these applications elicited only small current responses. However, when the first application was superimposed on a 2.5 s voltage step, both applications induced substantial current responses (bottom panel), albeit in opposite directions.

Figure 4. Substantial changes in the intracellular chloride concentration induced by local application of GABA.

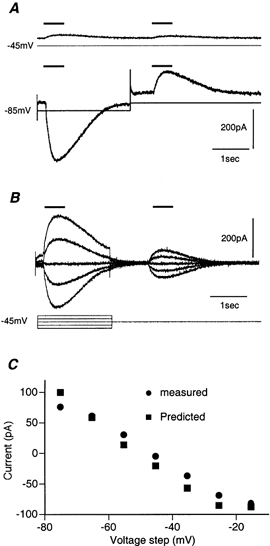
A, current response to two 500 ms GABA applications, at an interval of 2.5 s ([Cl⁻] _P= 15 mm). Upper trace, the response at a holding potential of -45 mV, close to the GABA reversal potential. Lower trace, the first GABA application was delivered during a voltage step to -85 mV. Note the strong inward current elicited by the first application and the smaller, but significant, outward current elicited by the second application. B, as in A, but the voltage step was varied between -20 and -80 mV. Both the magnitude and direction of the response to the second application depended on the response to the first application. Note also the large voltage-dependent outward current elicited by depolarization to -25 mV, on which the response to GABA is superimposed. C, the measured (•) and the predicted (▪) amplitudes of the second response as a function of the membrane potential during the first application.

This experiment shows that a current response to the first GABA application was sufficient to induce an opposite current response to the second application. This can be explained only if the first current response changed the intracellular chloride concentration. Accordingly, the GABA reversal potential was shifted from its original value (-45 mV) towards the value of the voltage step (-85 mV). As a result, the holding potential (-45 mV) was more positive than the new reversal potential and the second application would induce current in the opposite direction to the first one. This explanation is further supported by the results shown in Fig. 4B, where the amplitude and direction of the currents induced by the second GABA application depended on the value of the voltage step during the first application. The same results were obtained from all six neurones tested in this way. Thus local application of GABA clearly induced significant changes in chloride concentration within SCN neurones.

We quantitatively examined to what extent the chloride fluxes during the conditioning pulse predicted the amplitude of the response to the second application. To that end, the charge carried by each of the current responses to the first application was measured (see Methods). The net chloride charge was then calculated (eqn (6)), transformed into a concentration change (eqn (7)) and the chloride equilibrium potential estimated (eqn (3)). The predicted current evoked by the second application could then be calculated using eqn (2). The results of these calculations are shown in Fig. 4C, where the predicted (▪) and the measured (•) amplitudes of the second response were plotted as a function of the voltage step. The almost perfect fit suggested that, indeed, the chloride influx or efflux during the first application was sufficient to account for the change in the GABA reversal potential.

Bath application of GABA

Bath application of 100 μm GABA markedly increased the membrane conductance in all the experiments (n = 14). This conductance increase was calculated from the current responses to voltage steps before, during and after the application. The current responses in control conditions, in the presence of both GABA and bicuculline, or after washing GABA from the bath, were subtracted from the currents measured in the presence of GABA (Fig. 5A, top, middle and bottom panels, respectively). Therefore, the traces reflect only the current flowing due to GABA-induced conductance changes. The similarity of the current responses in all the three procedures showed that the response to bath application was reversible and mediated solely via GABA_A receptors. Similar results were found in all four cells tested with bicuculline.

As in the case of local application, the current-voltage relationship showed two conductance states (Fig. 5B). When the current at peak response was measured (▪) the slope of the current-voltage relationship (peak conductance) was reduced from 4.3 to 2.3 nS at voltage steps more negative than -70 mV. The mean conductance at the peak was 4.0 ± 2.0 nS at depolarised levels and 2.0 ± 1.0 nS at hyperpolarised levels (n = 14). A much stronger difference was observed when the current was measured at the end of the voltage step (•). The conductance dropped from 3.1 nS to 0.5 nS at more negative potentials. The averaged values were 3.4 ± 1.7 nS and 0.8 ± 0.7 nS for the depolarising and hyperpolarising ranges, respectively (n = 14). Thus, peak conductance was decreased by 49 ± 12 % from the resting potential range to the more hyperpolarised range, while the conductance at the end of the voltage steps was decreased by 74 ± 15 %. In view of the previous results, it is likely that the apparent time-dependent conductance change reflected both the voltage dependence of the GABA-induced conductance and the rearrangement of chloride ions according to the new membrane potential. The persistent GABA conductance demonstrated that, in neurones of the SCN, the GABA conductance does not inactivate. The similarity between the conductance values measured during bath application and those measured during local application further confirmed this conclusion (see Discussion).

Recovery of the GABA-induced current during the subjective day

To measure the recovery time course of the intracellular chloride concentration, we used a conditional train of GABA pulses to increase or decrease the intracellular chloride concentration. A short GABA test pulse was then delivered at different intervals. As shown in Fig. 6A, the train of GABA pulses elicited an outward current when the membrane potential was held at -40 mV and an inward current when -70 mV was used. The two responses were almost identical in the absolute value of the current and both declined to 18 % of the peak value within 5 s. As described above, this decline in the response was due to changes in the intracellular chloride concentration. As a result, the amplitude of the response to the test pulse was lower than the amplitude of the response to the conditioning train. It should be mentioned that the first pulse in the conditioning train and the test pulse induced the same conductance change (data not shown).

Figure 6. Time course of recovery of the response to GABA application in day experiments.

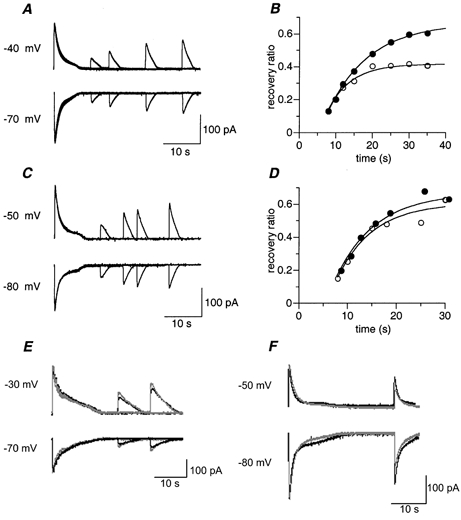
A, 4 superimposed current traces obtained during subjective day, each showing the response to the train of GABA pulses, followed by a short GABA test pulse delivered at different intervals. Membrane potential was held at either -40 mV (upper trace) or -70 mV (lower trace). B, time course of recovery from chloride accumulation (•) or depletion (○) for the results shown in A. Data are presented as the ratio between the amplitude of the test response and the amplitude of the first response. C and D, another experiment as described in A and B, but in this example the two recovery processes follow a similar time course. E and F, the recovery process is regulated by active mechanisms. E, the recovery process from chloride loading (upper traces) and chloride depletion (lower traces) at an ambient temperature of 26 °C (black traces) and 28 °C (grey traces). Note the 24 % increase in the amplitude of the response to the test pulse at the higher temperature. F, recovery at 30 s delay before (black traces) and after (grey traces) 1 mm furosamide application. Note the 40 % decrease in the test response amplitude in the recovery from chloride depletion and the 48 % reduction in the recovery from chloride loading.

When outward current was examined (loading the cell with chloride, Fig. 6A upper trace), increasing the delay between the conditioning train and the test pulse resulted in a monotonic increase in the test response amplitude. Usually a 55-85 % recovery was reached within 35 s delay. Complete recovery was observed only in one cell (n = 54). Furthermore, increasing the delay to the test pulse (up to 120 s) increased the amplitude to only 90 % of the original value (not shown). A similar phenomenon was observed when inward current was examined (depleting the cell of chloride, Fig. 6A lower trace). The results of these two processes are summarised in Fig. 6B, showing the ratio between the amplitude of the test response and the amplitude of the conditioning response, for chloride depletion (○) and loading (•). The recovery process, which followed an exponential time course with a time constant of 11.4 s (chloride loading) and 6.3 s (chloride depletion), reached steady state levels of 0.7 and 0.4, for loading and depletion, respectively.

The recovery from chloride depletion (as opposed to recovery from chloride loading) showed significant variation. In the example shown in Fig. 6C and D, both processes had similar time constants, 7.4 and 8.2 s for chloride loading and depletion, respectively. The averaged time constants, calculated for 5 cells (out of 27 measured during the subjective day) that showed a smooth monotonic recovery, were 7.5 ± 3.1 s for chloride depletion and 8.5 ± 2.3 s for chloride loading. It should be mentioned that only six cells (out of 54 from both in day and night experiments) showed identical rates of recovery for the two processes. Furthermore, although the recovery from chloride depletion was somewhat faster, its steady state levels were lower (0.6 ± 0.2 and 0.8 ± 0.1 for depletion and loading, respectively).

Before further characterising the recovery processes, it was necessary to eliminate the possibility that these observations reflected diffusion of chloride from or to the patch pipette. The difference between the recovery from chloride loading and depletion suggested that diffusion was not a prominent factor within the time window of 35 s. In addition, two further sets of experiments were performed. First, the temperature dependence of the recovery process was examined (n = 4, Zhang et al. 1991). Figure 6E shows an example of such an experiment. Raising the ambient temperature from 26 °C to 28 °C increased the response to the test pulse at 30 s delay by an average of 26 ± 10.4 %. The mean recovery time constant was reduced, resulting in a Q₁₀ of 11.5. This value is more than would be expected from a passive diffusion process (Q₁₀ < 1.8; Ungell, 1986) supporting an active mechanism. Second, the effect of furosamide and bumetanide, known non-selective inhibitors of chloride transporters (Jarolimek et al. 1999; Kakazu et al. 2000; Sung et al. 2000), was measured (n = 3). As shown in Fig. 6F, 1 mm furosamide decreased the recovery at 30 s after chloride loading by 48 % and after chloride depletion by 40 %. Similar results were obtained for the two other cells. These two findings confirmed that diffusion might be ignored within the first 35 s of the process.

Thus, given that the parameters measured in our experimental protocol reflect active cellular processes, it follows that two independent mechanisms operate in SCN neurones: one that removes intracellular chloride after loading and another, with different kinetics, that accumulates chloride in the cell after depletion.

Recovery of the GABA-induced current during the subjective night

A different behaviour was found in slices prepared during subjective night. Two examples are shown in Fig. 7. In one example (Fig. 7A and B) recovery is within the range recorded during subjective day (Fig. 6): 11.3 s for chloride depletion (○) and 16.0 s for chloride loading (•). However, 4 out of 27 showed no recovery from chloride depletion (Fig. 7C and D). In these cases, found only during subjective night, the amplitude of the test response after chloride depletion was independent of the delay after the conditioning train (Fig. 7D, ○). The recovery from chloride loading, on the other hand, had time courses similar to those measured during subjective day (10.8 s, •). Averaged time constants were calculated for 6 cells (out of 27) that showed a smooth monotonic recovery from chloride loading, of which 3 showed no recovery from chloride depletion; these were 16.1 ± 5.0 s for chloride loading (n = 6) and 10.5 ± 5.5 s for chloride depletion (n = 3). As with the subjective day experiments, recovery from chloride loading had slower time constants and reached higher steady state levels (0.8 ± 0.4 and 0.4 ± 0.3 for loading and depletion, respectively).

Figure 7. Time course of the recovery of the response to GABA application during subjective night.

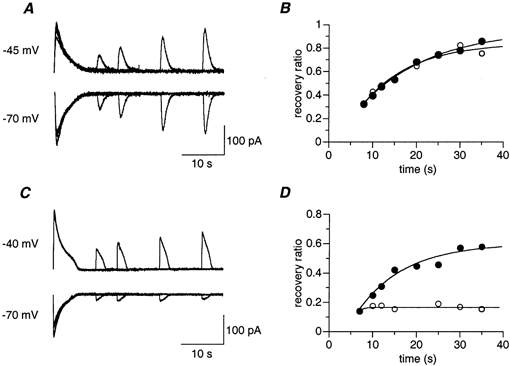
A–D, as in Fig. 6A–D, but for two experiments performed during subjective night. ○, recovery from chloride depletion; •, recovery from chloride loading. Note the lack of recovery from chloride depletion in C and D.

Change in chloride concentration

The data above show recovery of the amplitude of the GABA-induced currents. The following calculations were made to estimate the actual change in chloride concentration. First, using eqn (8), we calculated the expected change in reversal potential of the GABA-induced currents. Figure 8A shows the results of these calculations for the example shown in Fig. 6A. Eight seconds after conditioning, the GABA reversal potential increased by 12 mV when loading the cell with chloride (•) and decreased by 14 mV when the cell was depleted of chloride (○). This was followed by a gradual recovery of the GABA reversal potential to approach steady state levels, which were 5.5 mV above and 9.0 mV below the original reversal potential for chloride loading and depletion, respectively.

Figure 8. Calculating the time course of recovery of the intracellular chloride concentration (data are from Fig. 6A).

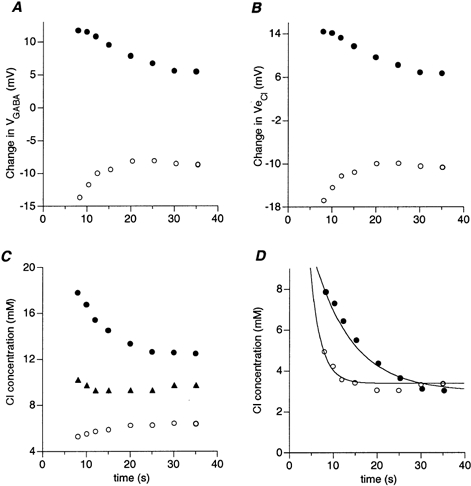
○, recovery from chloride depletion; •, recovery from chloride loading. A, time course of recovery of GABA reversal potential. B, time course of recovery of chloride equilibrium potential. C, time course of recovery of intracellular chloride concentration. The resting chloride concentration (▴) was about 9.5 mm. D, time course of recovery of absolute change in [Cl⁻] _i. The resting chloride concentration was subtracted from the data shown in C. Two exponential curves with time constants of 8.83 s (chloride loading) and 2.4 s (chloride depletion) were fitted to the results.

Next, using eqn (4), we calculated the actual change in chloride equilibrium potential (V_e,Cl). The results of these calculations are shown in Fig. 8B. As expected, the time course of the process was similar to that calculated for the recovery of the GABA reversal potential, but the magnitude of the change was larger. At 8 s delay, the change in V_e,Cl was -17 mV for chloride depletion (○) and 14 mV for chloride loading (•).

Once the change in the chloride equilibrium potential was calculated, the intracellular chloride concentration could be extracted using the Nernst equation (eqn (3)). The results of these calculations are shown in Fig. 8C. As expected, a decrease of 5 mm in the intracellular chloride concentration was sufficient to induce a 17 mV change in the chloride equilibrium potential (○). However, almost an 8 mmincrease in chloride concentration was needed to induce a 14 mV depolarisation in V_e,Cl (•).

To obtain the absolute change in chloride concentration, we subtracted the measured resting chloride concentration (▴) from the data (• and ○) shown in Fig. 8C. The results are shown in Fig. 8D for chloride loading (•) and depletion (○). Two exponential curves with time constants of 8.8 s and 2.4 s for chloride loading and depletion, respectively, fitted the results. This indicated that the process regulating the accumulation of chloride was faster than that regulating chloride removal.

Decrease in the efficiency of the chloride accumulation mechanism during subjective night

As shown in Fig. 6 and 7, the variability of the recovery process was relatively high. Of a population of 54 cells, only 11 showed smooth recovery processes from which time constants and steady state levels could be reliably extracted. This was partially due to the prolonged experimental protocol. We minimised this variability by measuring the recovery at a single time point, 30 s after conditioning. Although this procedure greatly reduced the extent of variation, we now had to calculate the amount of chloride that entered or left the cell during the response to the conditioning train. To do this, we used eqns (5), (6) and (7).

The results of 9 experiments performed during the subjective night and 13 performed during the subjective day are summarised in Fig. 9. The average resting chloride concentration (black columns) was 13.8 ± 8.5 mm in day (Fig. 9A) and 11.2 ± 4.7 mm at night (Fig. 9C). The discrepancy between this value and the actual concentration in the pipette solution was probably due to the known phenomenon of junction potential discussed above (Ng & Barry, 1995). Using Student's t test for paired samples we first compared the chloride concentration at 30 s (open columns) to the resting concentration (black columns). A significant difference was found in all cases (P values ranged between 1 × 10⁻² and 3 × 10⁻⁵). These results are in agreement with the observation that complete recovery was rarely observed. We then compared the concentration at 30 s (open columns) to the concentration at the end of the conditioning pulse (grey columns). In this case the only insignificant difference was found in night experiments when recovery from chloride depletion was examined (Fig. 9D). Hence, on average, there appears to be practically no recovery from chloride depletion in SCN neurones during subjective night.

Figure 9. Statistical analysis of the chloride recovery process.

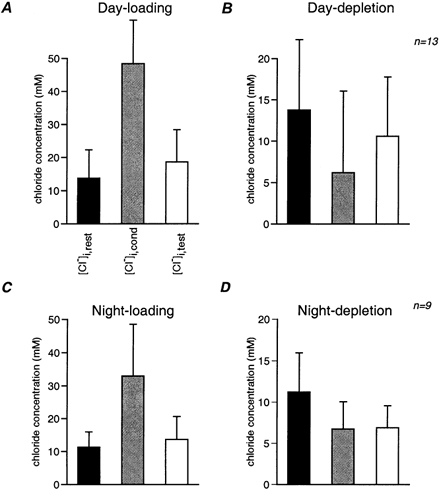
The intracellular chloride concentration is depicted at three time points: before the beginning of the trial (black columns), at the end of the conditioning train (grey columns) and after a delay of 30 s (open columns). These three concentrations were measured during the subjective day (A and B, n = 13 cells) and night (C and D, n = 9 cells) for recovery from chloride loading (A and C) and depletion (B and D). In loading trials, the chloride concentration increased as a result of the GABA conditioning train and then decreased after 30 s to close to the resting level. In depletion trials, the chloride concentration, which decreased during the conditioning train, only recovered in experiments performed during subjective day, while there was no recovery at night. Note that the averaged chloride concentration in day experiments (A and B) is insignificantly higher than in night experiments (C and D). Furthermore, loading also resulted in a higher chloride concentration during the day. This is due to choice of membrane holding potentials and does not indicate a genuine difference in the process of chloride loading during day and night. The chloride concentration at 30 s delay is significantly different from that at the onset of the conditioning pulse for all experiments.

DISCUSSION

In this work we used voltage-clamp methodology, combined with local application of GABA, to characterise the current induced by GABA and to examine the vulnerability and regulation of the intracellular chloride concentration. Our results suggest that: (a) the current induced by GABA is carried by both chloride and bicarbonate ions, lacks slow desensitisation processes and is moderately voltage dependent; (b) given the small size of SCN neurones, the influx and efflux of chloride is sufficient to induce a substantial change in chloride concentration; (c) there are two independent mechanisms regulating intracellular chloride level, one removing chloride from the cell and the other accumulating it in the cell; and (d) the mechanism that reintroduces chloride into the cell becomes less efficient during subjective night.

Characterisation of the GABA-induced current

The ionic specificity of the GABA-induced current was examined in this study by measuring its reversal potential, under different intra- and extracellular chloride concentrations (Fig. 2). The results suggest that 81.5 % of this current is carried by chloride ions. We assume, based on previous reports (Kaila, 1994), that bicarbonate carries the other 18.5 % of the current. However, given that the bicarbonate equilibrium potential is -10 mV (Kaila et al. 1993; Staley & Proctor, 1999), a discrepancy of 12 mV was found between our data and the expected equilibrium potential. There are several possible explanations for this disparity. (1) The bicarbonate equilibrium potential is not -10 mV. However, if this was the only source of the difference, bicarbonate equilibrium should have been around +50 mV, an unlikely possibility. (2) Other ion(s) participate in the GABA-induced current, probably small monovalent anions (Kaila, 1994). However, relative permeability of all other ions is rather low and cannot account for 18.5 % of the current. (3) The most reasonable explanation is that this discrepancy is due to the junction potential between the gluconate-containing patch pipette and the extracellular medium (Ng & Barry, 1995).

A major finding here is that chloride fluxes do, indeed, profoundly alter the intracellular chloride concentration. This was shown by several independent experiments, of which the most significant was the use of consecutive GABA applications (Fig. 4). In these experiments we showed that the current response to the first application changes the reversal potential and, thus, the driving force of the current induced by the second application. We demonstrated that the change in the response of the second application could be well predicted by calculating the amount of chloride entering or leaving the cell during the response to the first application. The idea that the GABA-induced current changes the intracellular chloride concentration and, hence, its own reversal potential has already been raised by several investigators (Huguenar & Alger, 1986; Akaike et al. 1987; Kunar & Augustine, 2000).

GABA-induced conductance does not desensitise

A second important result shown here is the lack of measurable desensitisation (Fig. 3 and 5). However, as demonstrated by Jones & Westbrook (1996), the speed of agonist application influences kinetic measurements. Thus, a fast transition to an inactive state, coupled with a slow application of the agonist, results in the absence of measurable desensitisation of the current. Since we used a relatively slow application technique we cannot exclude a desensitisation process with a time constant in the order of tens of milliseconds (Jones & Westbrook, 1995). However, our findings clearly show that SCN neurones are devoid of the commonly observed, slow (1-20 s) desensitisation process (Mierlak & Farb, 1988; Tauck et al. 1988). The observations that bath application induced a persistent GABA conductance (Fig. 5) strengthen this conclusion. Desensitisation has been attributed to the β subunit of the pentameric GABA_A receptor (Sigel et al. 1990) and, in particular, to the most common β₂ subunit (Verdoorn et al. 1990). SCN neurones do not express the β₂ (O'Hara et al. 1995) and β₃ subunits (Gao et al. 1995) and it is, therefore, possible that the unique subunit composition of the GABA_A receptors in the SCN underlies this lack of desensitisation.

The absence of desensitisation seems particularly appropriate for regulating network excitability via GABA_A receptors in a non-synaptic mechanism. Assuming a constitutive release of GABA from SCN neurones, a certain level of GABA would be constantly present in the extracellular space. This would activate mainly extrasynaptic, non-desensitising GABA_A receptors, permeable to chloride. Such tonic release of GABA would serve to modulate excitability levels rather than transmission of synaptic signals. Several lines of circumstantial evidence support this hypothesis. Firstly, the neurones in the SCN are closely packed, severely restricting the extracellular space (van den Pol, 1980). Thus, even small quantities of GABA may significantly raise extracellular GABA concentration. Secondly, it has been demonstrated that the GABA content of the SCN undergoes circadian oscillations (Aguilar Roblero et al. 1993). Thirdly, in addition to the GAD₆₅ isoform of the enzyme that synthesises GABA, SCN neurones also express the GAD₆₇ isoform (Gao & Moore, 1996), which may be associated with tonic GABA synthesis and release (Feldblum et al. 1993). Fourthly, vesicular release from dendrites has been demonstrated in SCN neurones (Castel et al. 1996).

Characterising the process of chloride regulation

Transport of chloride both into and out of the cell showed incomplete recovery. One possible explanation is that the regulation mechanism was inactive within a certain range of chloride levels (Aronson, 1985). It is also possible that the incomplete recovery was due to the sub-optimal temperature used in the experiments or to the long duration of the experimental procedure, causing a rundown of essential cytosolic factors (Russell, 2000). Another possibility is that this lack of full recovery was due to the experimental protocol, in which the holding potential alternated in successive trials (see Methods), and the conditioning train started before the chloride concentration had returned to its resting level. Hence, the amplitude of the response to the conditioning pulse was actually larger than expected and thus could never be reached by the response to the following test pulse.

Recovery from chloride depletion was found to be faster than recovery from chloride loading, a result clearly observed when comparing either the actual changes in intracellular chloride concentration (Fig. 8D) or the response amplitudes (Fig. 6A). As mentioned above, the recovery was incomplete; the steady state chloride levels reached at the end of the recovery processes were 3 mm above or below the control level. However, as expected from the logarithmic nature of the Nernst equation, the amplitude of the test response at the end of the recovery process was higher for chloride loading. The fact that each recovery process was fitted by a single exponent implies that they each involve a single transporter. Staley & Proctor (1999) also found that the recovery from chloride loading followed a single exponential process. Furthermore, their time constant for the recovery of the intracellular chloride concentration was 3.5 s, i.e. within the range found here.

The data in Fig. 8D allowed calculation of the flux of chloride through these hypothetical transporters. Assuming an 8 μm diameter cell, the calculated flux was 7.5 × 10⁻¹⁶ mol min⁻¹. Taking the rate described for the GABA transporter (2 × 10⁻²⁴ mol min⁻¹ transporter⁻¹; Quick et al. 1997), this gives 3.5 × 10⁸ transporter molecules in an SCN neurone. We used 8 μm as a representative value of cell diameter based on van den Pol's (1980) thorough morphological study of the SCN in rat. He found that the average cell diameter in the dorso-medial region, in the vicinity of the third ventricle, where most of our recordings were made, was 7.83 ± 0.91 μm. This value for cell diameter determined the calculated change in [Cl⁻] _i and thus is critical for our evaluations of the recovery process. Some of the variation encountered in our experiments may be due to this parameter.

The averaged resting chloride concentration, about 10 mm (Fig. 9), is twice the expected value for the patch pipette (5 mm). This discrepancy might be due to either the known junction potential (Ng & Barry, 1995), or a gradient of chloride between the cell cytoplasm and the pipette caused by the constitutive action of a chloride transporter or by a concentration gradient along the cell. The GABA application is likely to effect not only the somatic membrane but the proximal dendrites as well. Since a much larger change in [Cl⁻] _i is expected in the smaller volume of the proximal dendrites and since a gradient between dendrites and soma can exist (Staley & Proctor, 1999), the high value of the intracellular chloride concentration may, therefore, reflect a genuine difference.

Circadian alterations in chloride regulation

Comparison between day and night experiments revealed that, although recovery from chloride loading was similar over the diurnal cycle, recovery from chloride depletion was significantly less efficient at night (Fig. 9). In fact, the averaged [Cl⁻] _i after 30 s was similar to the calculated [Cl⁻] _i after the conditioning train. This is rather surprising, since the kinetic measurements revealed that at least some cells show recovery (Fig. 7A). The only explanation is that our volume assumptions may have led to an overestimation of the amount of chloride efflux in some experiments (see above). However, a better estimation of cell volume would not have detracted from the significant difference between day and night that we found in the recovery from chloride depletion.

These results led to the following conclusions. (a) The difference between the processes supports, once again, the involvement of two different transport mechanisms in intracellular chloride regulation. (b) The mechanism responsible for the reintroduction of chloride is, for an as yet unknown reason, less efficient during subjective night. The latter conclusion is of major importance. Firstly, it explains our previous observations on the dual effects of GABA. Regardless of which mechanism may participate in chloride homeostasis, a decrease in the efficiency of the inwardly directed transport undoubtedly decreases the steady state level of [Cl⁻] _i. This increases the inhibitory effect of GABA_A receptors and, therefore, GABA would be expected to act as an inhibitory neurotransmitter during subjective night. Secondly, the decrease in efficiency of a transport system is especially interesting, as it brings us one step closer to bridging the gap between the well-known and thoroughly studied molecular mechanisms of the circadian clock and its manifestation as a rhythmic change in the firing rate of neurones.

In summary, SCN neurones express a large number of GABA_A receptors that seem to be especially suitable to create a modifiable, tonic chloride conductance. In addition, due to circadian alterations in the efficiency of the inwardly directed chloride transport system, the chloride concentration in these neurones undergoes circadian changes. We hypothesise that the GABA conductance and the change in chloride concentration enable the local GABAergic network within the SCN to synchronise excitability changes in the SCN neurones and thereby organise the individual cellular pacemakers into a functional biological clock.