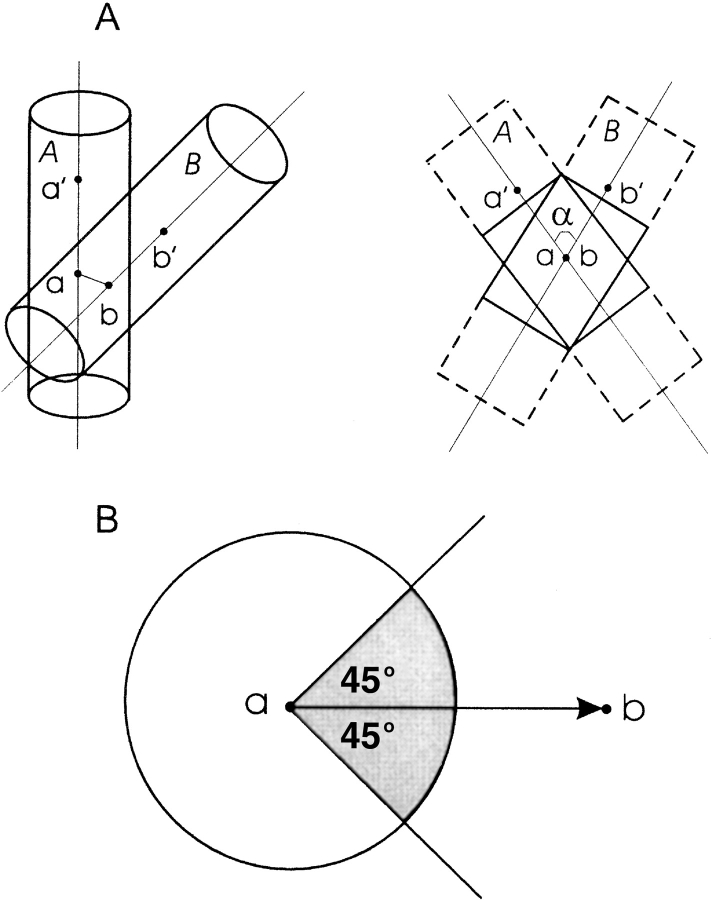
Figure 1.

Parameters of helices used in the analysis. (A) Definition of the interacting segments. A pair of packed helices is represented by cylinders A and B, with the main axes defined by aa′ and bb′, and ab orthogonal to the main axes. The helix packing angle α is the dihedral angle a ′abb′. Point a is the center of mass of seven C^α atoms in helix A with the center C^α being the closest to a C^α atom in helix B. Point a′ is the center of mass of C^α atoms in a fragment from point a to the C or N terminus of the helix, whichever is longer. Points b and b′ in helix B are defined similarly. The length L of packed helical fragments (shown as solid rectangles) is calculated as L = 2Rcot(α/2), where R = 5Å is the helix radius. Outstanding parts (dotted lines) are deleted. (B) Definition of the helix–helix interface. Viewed along the axis a′ a of helix A, vector ab is in the center of a 90° interface sector (shaded).