Abstract
In this study related to human brain SPECT imaging, simulation of half-cone-beam collimation and helical-path data acquisition is performed. We discuss problems related to circular-orbit acquisition using cone-beam collimation, such as shoulder interference resulting in object truncation, and insufficient sampling of the object resulting in axial distortions in the reconstructed images. We demonstrate that a triple-camera SPECT system with half-cone-beam collimation and single-revolution helical-path acquisition eliminates both issues and offers substantially improved sampling and almost artifact-free reconstruction of the object.
Index Terms: Cone-beam, half-cone-beam, helical-path, sampling sufficiency, SPECT, triple-camera
I. Introduction and Motivation
In single photon emission computed tomography (SPECT) [1] collimator configuration plays a major role. Collimator performance, often characterized by its sensitivity, spatial resolution, and field of view (FOV), depends partially on the size of the imaged object and its distance from the detector. In human brain SPECT imaging converging collimators offer improved sensitivity and resolution [2]–[6] compared to parallel-hole collimators widely utilized in clinical SPECT. Two well-known converging collimator types are fan-beam (FB) [2], [3] and cone-beam (CB) [3], [4]. The FB collimator converges only transaxially and for typical imaging scenarios offers less sensitivity compared to a CB collimator. Due to image magnification both axially and transaxially, CB collimators are generally utilized on gamma cameras with a relatively large FOV to avoid data truncation. In brain imaging, however, shoulder interference limits the FOV of the full-cone-beam (FCB) collimator in the desired location of the patient's head, and the lower (caudal) region of the brain is truncated [see Fig. 1(a)]. Increasing the radius of rotation (ROR) to clear the shoulders worsens the spatial resolution and may require a larger FOV to image the entire brain. To address this issue various collimator configurations have been proposed in the past, including tilted-cone-beam [5], [7], half-cone-beam [8], [9] and offset-astigmatic-beam [10], [11] collimators. Fig. 1(b) illustrates the particular advantage of using the half-cone-beam (HCB) collimator designed specifically for brain imaging. The HCB collimator allows close positioning of the γ-camera to the patient's head without interfering with the shoulders. We have studied HCB collimation closely and have found ways to effectively utilize it in human brain SPECT. The conventional single circular-orbit (SCO) scan of the brain using HCB collimation produces severe axial distortions in the reconstructed image due to insufficiently sampled projection data. We demonstrate that this problem can be alleviated using a triple-camera SPECT system and helical-path acquisition, in which the patient is translated axially as the gantry rotates 360 degrees in a circular orbit.
Fig. 1.
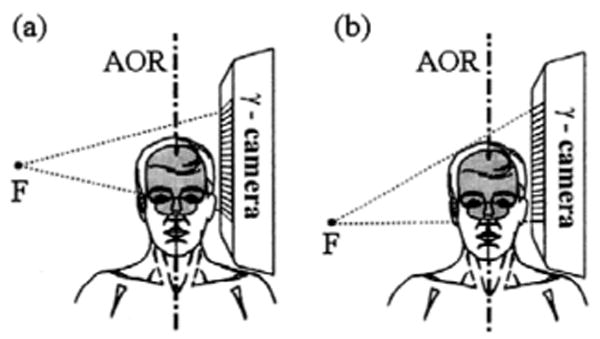
Sketches of the FCB (a) and HCB (b) collimators with a close positioning to the patient's head. F is the focal point of the collimator.
II. Methods and Simulation
To study the effects of HCB collimation in brain SPECT, we simulate a Defrise disk phantom—a cylinder filled with water and six solid equally-spaced concentric disks made out of a material (e.g., polymethylmethacrylate) with an attenuation coefficient similar to that of water. The dimensions of the phantom (diameter is 18.50 cm; length is 12.78 cm) are chosen to generally resemble a human head. The thickness of the solid disks is 1.08 cm each, with a 0.90 cm water gap between them filled with activity. The γ-camera FOV, 46.0 cm transaxially and 23.0 cm axially, is chosen to be similar to the general-purpose triple-camera SPECT system (Triad XLT, Trionix Research Laboratories, Twinsburg, OH) at the Duke University Medical Center (DUMC) SPECT Research Laboratory. The HCB collimator is also simulated in accordance with the existing collimator currently used by our research group. The focal length of the HCB collimator is 50.0 cm measured from the patient side of the collimator, and the collimator thickness is 4.0 cm. The focal point is shifted axially by 11.5 cm towards the base of the phantom as measured from the center of the camera. The detector intrinsic resolution, modeled as Gaussian, is 0.35 cm full width at half maximum (FWHM). The camera axis of rotation (AOR) is perpendicular to the imaged disks, and the ROR equals 13.0 cm. The phantom is centered on the AOR. During circular-orbit acquisition the bottom disk of the phantom is coplanar with the transaxial focal plane. The HCB collimator and the Defrise disk phantom used in the simulations are illustrated schematically in Fig. 2.
Fig. 2.
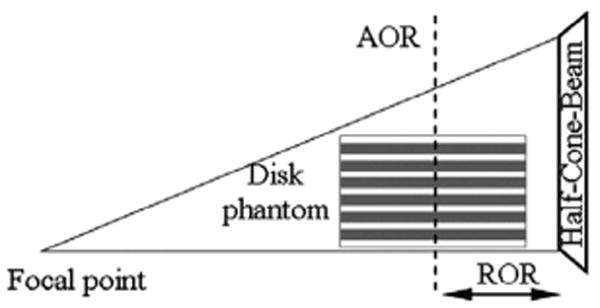
A sketch of the HCB collimator and the Defrise disk phantom used in the simulations. Focal length is 50 cm, ROR is 13 cm. The dark stripes in the phantom sketch correspond to the solid disks. The white stripes are water filled with activity.
Iterative reconstruction of the phantom, after simulating the forward-projected data, is performed using a ray-driven ordered-subsets expectation maximization (OSEM) algorithm [12] with 8 subsets and 10 iterations. Image voxels in forward projections and reconstruction were cubical with an edge length of 0.18 cm.
A. Circular-Orbit Acquisition
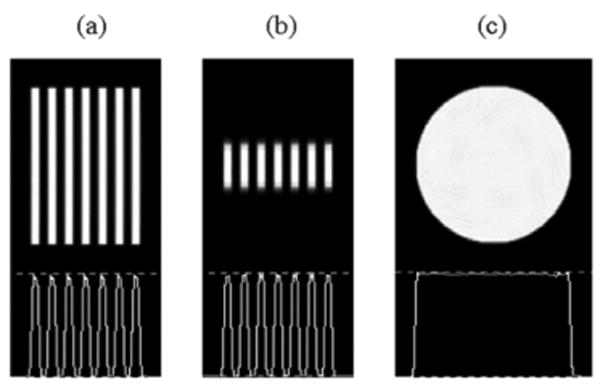
As mentioned in the introduction, an SCO scan using converging collimation (except for FB) results in axial distortions of the reconstructed image due to insufficient sampling. Indeed, only a single focal plane perpendicular to the AOR is sufficiently sampled according to Tuy's sufficiency condition [13]. The severity of the artifacts increases with increasing cone angle. A 360-degree circular orbit of the camera rotating around the AOR is simulated using two-degree angular sampling. Fig. 3 illustrates the OSEM reconstructed Defrise disk phantom using simulated SCO data acquisition with FCB, HCB and parallel-hole collimations in comparison with the disk phantom bitmap. The problem with shoulder interference for the FCB collimator is deliberately omitted in this example to illustrate only the artifacts due to insufficient sampling with SCO acquisition and convergent-beam collimation.
Fig. 3.
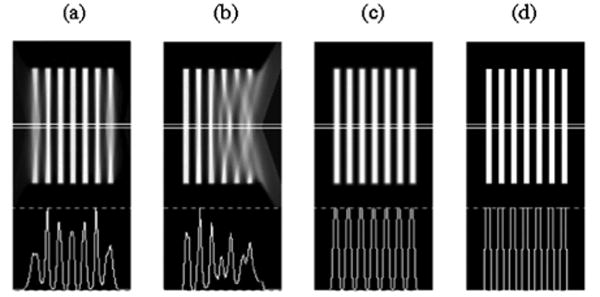
Reconstructed Defrise disk phantom using simulated FCB (a), HCB (b) and parallel-hole (c) collimation with circular-orbit acquisition in comparison with the phantom bitmap (d). Central sagittal slices and their profiles are shown. Reconstructions are performed using the OSEM algorithm with 8 subsets and 10 iterations.
B. Helical-Path Acquisition
The concept of helical-path acquisition is not novel and has been successfully applied to X-ray CT scans [14], pinhole [15] and long-object SPECT imaging [16]–[18], where the FOV of the γ-camera is not sufficiently large to image the entire object. This concept can also be effectively applied to human brain SPECT with cone-beam collimation to satisfy the data sufficiency condition.
As the camera revolves 360 degrees in a circular orbit around the AOR, the phantom is simultaneously translated axially across the FOV with a constant velocity. In the reference frame of the phantom the focal point of the collimator moves in a helical trajectory around the phantom (see Fig. 4). This kind of trajectory allows every point in the object to be sampled by the transaxial focal plane of the HCB collimator perpendicular to the AOR, which is essential for sufficient sampling.
Fig. 4.
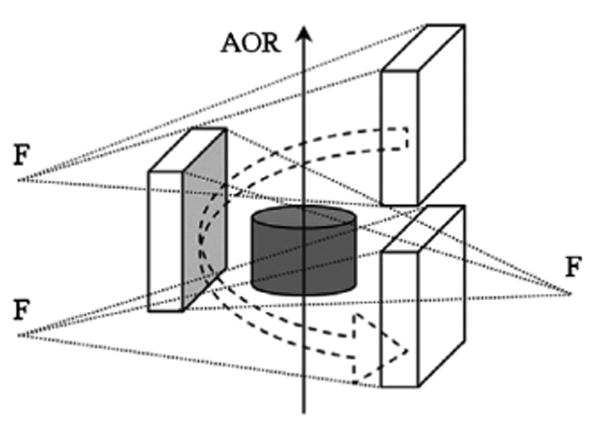
A 360-degree helical rotation of a single camera around a cylindrical phantom. F is the focal point of the HCB collimator utilized on the camera.
C. Sampling Sufficiency Condition
Sampling sufficiency criteria for cone-beam collimation of truncated and non-truncated projection data are described in [13], [16], [19]. Geometrically, it can be stated as in [19]: “if on every plane that intersects the object there exists at least one cone-beam source (focal) point, then the object can be reconstructed”. This is demonstrated in a 2D example [Fig. 5(a)] of a disk scanned in a circular orbit with a fan-beam collimation. In this example, for the disk to be sufficiently sampled, the focal point F has to move through an angular range of (180 + β) degrees around the disk till it reaches point F'. Then any plane that intersects the disk will cut through the focal point trajectory and the sampling sufficiency condition is satisfied. If 2α is the 2D cone-beam angle (fan-angle), then noticing that β = 2α, the sufficiency condition is referred to as a “ π plus fan-angle” requirement [16]. For a triple-camera SPECT system with a 120-degree separation between the cameras, the required rotation range is reduced to (π/3 + 2α) degrees for each camera, which is illustrated schematically in Fig. 5(b). This condition is also valid for FCB collimation with helical-path acquisition satisfying minimal pitch requirements [16], [18].
Fig. 5.
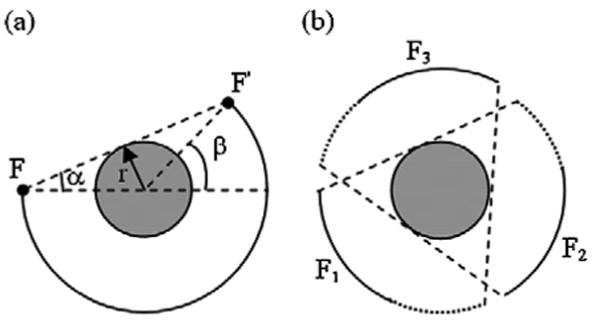
Illustration of the 2D disk sampling sufficiency condition using fan-beam collimation in a single-camera SPECT with a (180 + 2α) degree circular rotation (a), and a triple-camera SPECT with a (60 + 2α) circular rotation per camera (b). In (a), F and F' are the initial and final positions of the collimator focal point circling around the disk. In (b), F1, F2 and F3 are the circular trajectories of the focal points of three collimators on a triple-camera SPECT system. The solid curves correspond to the 60-degree rotation of the cameras, while the dotted curves show the additional 2α-degree rotation needed for sufficient sampling.
For parallel-hole collimation a 180-degree single-camera rotation is sufficient for a complete reconstruction. To our knowledge, the sampling sufficiency condition for HCB collimation has not been developed yet. We hypothesize that the condition is similar to that of the FCB collimation, but presumably is not identical to it with helical-path acquisition due to axial data truncation beyond the transaxial focal plane of the HCB collimator perpendicular to the AOR. Despite the axial data truncation, the results (discussed in Section III) indicate that the sampling criteria described above for FCB are reasonable enough for HCB collimation to provide undistorted reconstructions. We call the “π plus fan-angle” requirement a “near-sufficient” sampling condition for HCB collimation. Further investigation quantifying the sufficiency condition for HCB collimation is needed.
To demonstrate the problem of insufficient sampling we simulate a 360-degree helical-path acquisition of the Defrise disk phantom projection data using a single-camera SPECT with HCB collimation and reconstruct it iteratively using the OSEM algorithm. The description of the phantom is given in the beginning of Section II. In the simulation, the phantom is initially positioned completely outside the FOV of the camera, and enters the FOV as the camera starts rotating around the AOR. The translation of the phantom is only axial, and is synchronized with the rotation of the camera. The total translation distance is 17.0 cm. Given that the phantom length is 12.78 cm, the distance between the bottom of the phantom and the edge of the camera FOV, which is also the transaxial focal plane of the HCB collimator, reaches 4.2 cm. The bottom disk of the phantom is the least scanned one due to its truncation throughout the most of the acquisition. For a near-sufficient sampling of the bottom disk (and thus, the entire phantom) the camera needs to rotate (180 + β) degrees starting from the point where the disk is fully observed in the FOV. The angle β = 29 degrees is easily derived from the geometry of the simulated phantom and camera rotation. The required rotation of 209 degrees around the bottom disk cannot be fulfilled with a 17.0 cm translation, since the scan range of the bottom disk is only 89 degrees. The under-scanning results in artifacts in the reconstructed images of the bottom three disks (see Fig. 6). A double-camera SPECT system is not helpful in this case due the required rotation range of 180 degrees per camera. If, however, a triple-camera system is used instead with the same scanning parameters, the 89-degree rotation of each camera satisfies the near-sufficient sampling condition for HCB collimation.
Fig. 6.
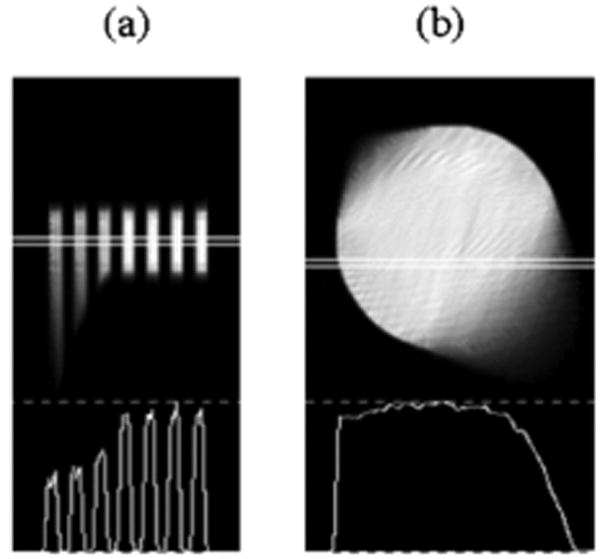
OSEM reconstructed (8 subsets, 10 iterations) disk phantom using simulated single-camera HCB collimation with helical-path acquisition. (a) sagittal slice close to the edge of the phantom and its profile reveal three distorted disks, which where not sufficiently sampled; (b) distorted image of the transaxial slice of the least sampled disk (i.e., the left-most disk in (a)).
In clinical brain SPECT (e.g., using a Triad XLT scanner), the typical distance between the bottom of the patient's brain and the edge of the FOV rarely exceeds 3.0 cm because of the shoulder interference and detector material between the shoulders and the effective FOV. This is slightly less than the value of 4.2 cm used in our simulations for a single-revolution helical path. Alternative scanning trajectories may be required for a sufficient sampling in a clinical study. For instance, a 720-degree (double-revolution) helical trajectory may be used in acquisitions [20], reducing the pitch of the helix by a factor of two, or a “circle + helix” trajectory, where the acquisition starts with a 360-degree circular orbit of the camera, then proceeds in a helical path with the brain slowly moving out of the FOV. Comparison of variable pitch helical trajectories is beyond the scope of this paper.
III. Results
A. Triple-Camera SPECT Using HCB Collimation and Helical-Path Acquisition
As discussed in Section II.C, a triple-camera SPECT system with HCB collimation and 360-degree helical-path acquisition with a 17.0 cm pitch provides near-sufficient sampling. Reconstructed images of the simulated Defrise disk phantom are shown in Fig. 7. The disks are well-reconstructed and the images are artifact-free.
Fig. 7.
OSEM reconstructed (8 subsets, 10 iterations) disks using simulated triple-camera HCB collimation with helical-path acquisition. (a) central sagittal slice; (b) sagittal slice close to the edge of the phantom; (c) transaxial slice of the least sampled disk (i.e., the left-most disk in (a)). Profiles of the reconstructed images are included.
B. Reconstruction With Attenuation Compensation and Poisson Noise
Until now we have assumed an ideal case of data acquisition without attenuation in the phantom or image noise. These factors, however, are always present in clinical studies and may play a major role in image reconstruction. Attenuation of photons in the object may result in poorly reconstructed images, especially in the central part of the object, if not accounted for. Adding attenuation compensation and statistical noise in our simulations, we demonstrate that the proposed method of HCB collimation with helical-path acquisition using a triple-camera SPECT system will be effective in clinical studies.
Attenuation is simulated within the forward-projection and OSEM reconstruction algorithms using a uniform attenuation map based on the phantom dimensions. Attenuation coefficient for water μ = 0.15 cm−1 is used in the simulations. Noisy projection data are obtained by sampling from Poisson distribution, where distribution means were given by the simulated noise-free projection data. The number of counts in the noise-free projection data was scaled down to the average number of counts typically acquired in clinical brain studies (a total of ∼ 2.7 × 106 counts per camera for a triple-camera SPECT system at DUMC). The effects of the attenuation and noise on forward-projected data of the Defrise phantom are shown in Fig. 8. Reconstructed images of the disks with attenuation compensation and noise are shown in Fig. 9(a). To reduce the noise, the images may be post-filtered using a von Hann filter with a cutoff frequency fc = 1.4 cycles/cm [see Fig. 9(b)]. The disks are well-reconstructed and undistorted.
Fig. 8.

Forward projections of the disk phantom simulated without attenuation and Poisson noise (a), with attenuation (b), and with attenuation and noise (c).
Fig. 9.
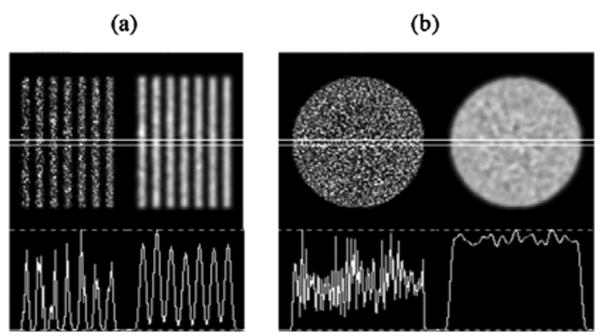
Reconstructed images of the disks with attenuation compensation and Poisson noise. (a) central sagittal view of the phantom is shown with non-filtered (left) and post-filtered (right) images and their profiles; (b) central transaxial disk is shown with non-filtered (left) and post-filtered (right) images and their profiles. Post-filtering is done using a von Hann filter with fc = 1.4 cycles/cm cutoff frequency.
C. Simulation and Reconstruction of the 3D Hoffman Brain Phantom
To study the effect of the proposed HCB collimation with helical path acquisition on an actual human brain reconstruction, we simulate the 3D Hoffman brain phantom [21] similarly to the Defrise phantom described above. The phantom bitmaps include 19 different transaxial brain slices. The brain measures 12.7 cm in cranial-caudal (top-bottom), 12.2 cm in trans-lateral (left-right) and 17.3 cm in anterior-posterior dimensions. Similar to the Defrise phantom simulation, a triple-camera SPECT system is used in simulations of the HCB collimation and 360-degree helical-path acquisition of the brain phantom data. To satisfy the sampling sufficiency condition discussed in Section II.C, the pitch of the helix was 16.0 cm. Iterative reconstruction is performed using the OSEM algorithm with 8 subsets, 10 iterations and 0.19 cm of cubical voxel width. The reconstructed images of four transaxial, one central sagittal and one central coronal brain slices and their profiles are shown in Fig. 10 in comparison with the brain bitmaps. No severe artifacts are observed in any of the reconstructed images.
Fig. 10.
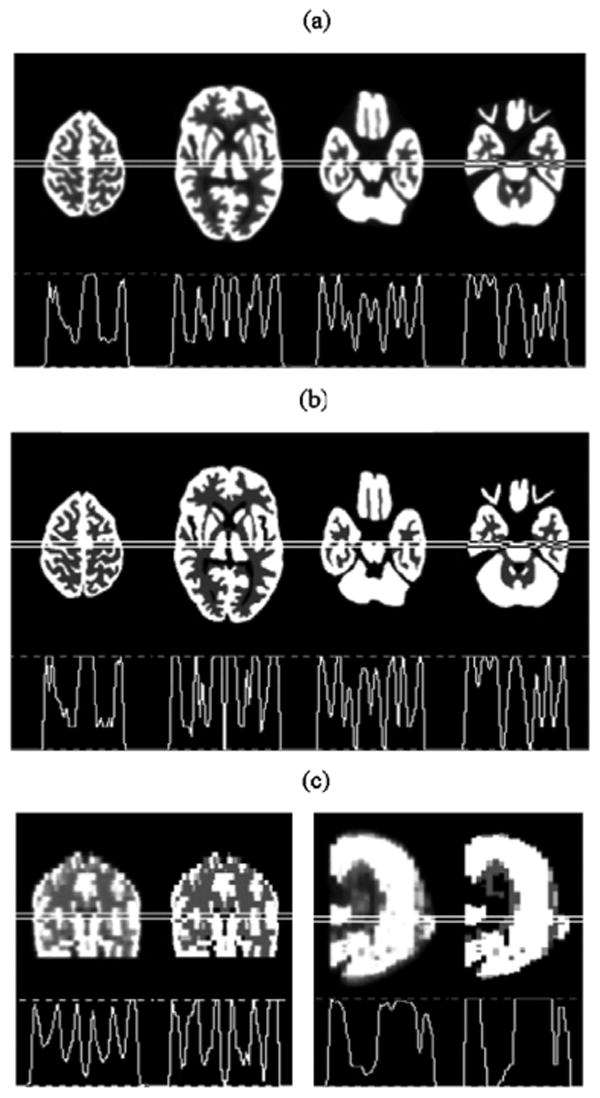
OSEM reconstructions (8 subsets, 10 iterations) of a simulated 3D Hoffman brain using HCB collimation and helical-path acquisition on a triple-camera SPECT system in comparison with the brain bitmaps. Four reconstructed transaxial slices (a) in the cranial-to-caudal order of the brain, with one cranial, one central and two caudal slices are compared with the bitmaps of the same slices (b). Reconstructions and bitmaps are also compared for central coronal (c) and central sagittal (d) slices. Profiles of all the images are included.
IV. Discussion
Brain SPECT imaging in clinical studies is typically performed with parallel-hole collimators and circular-orbit data acquisition. Convergent-beam, namely full-cone-beam collimators offer improved sensitivity and spatial resolution of the images compared to the parallel-hole collimators. Their utilization in brain SPECT, however, may be problematic for two reasons: 1) due to the γ-camera interference with patient's shoulders the caudal part of the brain is truncated; 2) a circular-orbit acquisition causes insufficient sampling and results in axial distortions in the reconstructed images. The alternative to the FCB collimator is a half-cone-beam collimator designed specifically for brain imaging. Although utilization of the HCB collimator eliminates truncation of the caudal brain due to shoulder interference, a circular-orbit data acquisition still results in axially distorted images due to incomplete sampling. To resolve the sampling problem we studied the possibility of acquiring data with a helical trajectory of the HCB collimator. This is achieved by translating the patient axially as the gantry rotates in a circular orbit. We demonstrated using simulations of the Defrise disk and 3D Hoffman brain phantoms that application of this technique on a triple-camera SPECT system provides considerably improved sampling and well-reconstructed and practically undistorted images even with a single (360-degree) revolution and a large pitch. To achieve similar sampling with double and single-camera SPECT systems the pitch should be smaller by factors of 2.0 and 2.3 correspondingly, based on required rotation ranges described in Section II.C.
Although a single-revolution helical-path acquisition is a good example of how a triple-HCB SPECT system may resolve the issues of truncated brain and insufficient axial sampling, it may not be the optimal scanning trajectory due to a smaller number of counts coming from the bottom of the brain that is being in the FOV for only 25–30% of total scan time. A “circle + helix” acquisition described in Section II.C may be more effective. If the brain is in the FOV during a 360-degree circular-orbit scan, HCB sensitivity is about twice of that for a parallel-hole collimator and about 50–60% more than a fan-beam collimator [9] (depending on collimator resolution). The efficiency of a helical scan is half of a circular, provided acquisition times for the circular and helical scans are equal. Thus, the “circle + helix” acquisition using HCB collimation offers ∼ 50% total gain in efficiency compared to an equal-time circular-orbit scan using a PB collimator. Comparison with a fan-beam collimator also yields 25–30% gain in favor of HCB collimation. It should be noted that the efficiency gain is averaged over the entire brain. Due to helical-path acquisition the bottom of the brain will have lesser counts than the top, but will still be comparable to PB collimation. The “circle + helix” trajectory is currently being investigated by our group and more detailed experimental data comparing HCB, FB and PB performances (e.g., sensitivities) will be acquired.
V. Conclusion
The HCB collimation using helical-path acquisition in brain SPECT imaging resolves the issues of the caudal brain truncation due to interference with patient's shoulders and axial distortions due to insufficient sampling of the brain. Reconstructed images of the disk and brain phantoms were practically artifact-free. We demonstrated that the technique is not affected by the image noise present in clinical studies, and the attenuation can be compensated for. The HCB collimation using helical-path acquisition may offer a potential improvement over conventional parallel-hole and fan-beam collimations, and has never been applied in clinical brain SPECT imaging before.
Acknowledgments
This work was supported by the National Institute of Neurological Disorders and Stroke, and by the National Cancer Institute of the National Institutes of Health under Grants R01 NS054797 and R01 CA76006.
Contributor Information
Ruben Ter-Antonyan, Department of Radiology, Duke University Medical Center, Durham, NC 27710 USA (e-mail: ruben@dec3.duhs.duke.edu).
Ronald J. Jaszczak, Department of Radiology, Duke University Medical Center, Durham, NC 27710 USA and also with the Department of Biomedical Engineering, Duke University Medical Center, Durham, NC 27710 USA.
James E. Bowsher, Department of Radiation Oncology, Duke University Medical Center, Durham, NC 27710 USA.
Kim L. Greer, Department of Radiology, Duke University Medical Center, Durham, NC 27710 USA
Scott D. Metzler, Department of Radiology, University of Pennsylvania, Philadelphia, PA 19104 USA.
References
- 1.Jaszczak RJ, Coleman RE, Lim CB. SPECT: Single photon emission computed tomography. IEEE Trans Nucl Sci. 1980;NS-27(no 3):1137–1153. [Google Scholar]
- 2.Jaszczak RJ, Chang LT, Murphy PH. Single photon emission computed tomography using multi-slice fan beam collimators. IEEE Trans Nucl Sci. 1979;NS-26:610–618. [Google Scholar]
- 3.Tsui BMW, et al. Design and clinical utility of a fan beam collimator for SPECT imaging of the head. J Nucl Med. 1986;27:810–819. [PubMed] [Google Scholar]
- 4.Jaszczak RJ, Floyd CE, Manglos SH, Greer KL, Coleman RE. Cone beam collimation for single photon emission computed tomography: Analysis, simulation and image reconstruction using filtered backprojection. Med Phys. 1986;13(no 4):484–489. doi: 10.1118/1.595854. [DOI] [PubMed] [Google Scholar]
- 5.Jaszczak RJ, Greer KL, Coleman RE. SPECT using a specially designed cone beam collimator. J Nucl Med. 1988;29:1398–1405. [PubMed] [Google Scholar]
- 6.Park MA, Moore SC, Kijewski MF. Brain SPECT with short focal-length cone-beam collimation. Med Phys. 2005;32(no 7):2236–2244. doi: 10.1118/1.1929208. [DOI] [PubMed] [Google Scholar]
- 7.Grangeat P, et al. Cone-beam SPECT with a tilted detector. Comput Med Imaging Graph. 1993;17(no 45):279–287. doi: 10.1016/0895-6111(93)90018-i. [DOI] [PubMed] [Google Scholar]
- 8.Jaszczak RJ, Li J, Wang H, Jang S, Coleman RE. Half-cone beam collimation for triple-camera SPECT systems. Eur J Nucl Med. 1994;21(no 10):27. [PubMed] [Google Scholar]
- 9.Li J, et al. Half-cone beam collimation for triple-camera SPECT systems. J Nucl Med. 1996;37(no 3):498–502. [PubMed] [Google Scholar]
- 10.Hawman EG, Hsieh J. An astigmatic collimator for high sensitivity SPECT of the brain. J Nucl Med. 1986;27:930. [Google Scholar]
- 11.Holmes RA, Logan KW, Hasselquist BE, Hawman EG, Hsieh J. Clinical evaluation of an astigmatic collimator for high sensitivity SPECT imaging of the brain. J Nucl Med. 1987;28(no 4):576–577. [Google Scholar]
- 12.Hudson HM, Larkin RS. Accelerated image reconstruction using ordered subsets of projection data. IEEE Trans Med Imag. 1994;13(no 4):601–609. doi: 10.1109/42.363108. [DOI] [PubMed] [Google Scholar]
- 13.Tuy HK. An inversion formula for cone-beam reconstruction. SIAM J Appl Math. 1983;43(no 3):546–552. [Google Scholar]
- 14.Kalender WA, Goldman LW, Fowlkes JB, editors. Medical CT and Ultrasound: Current Technology and Applications. College Park, MD: AAPM; 1995. Principles and performance of spiral CT; pp. 379–410. [Google Scholar]
- 15.Metzler SD, Greer KL, Jaszczak RJ. Helical pinhole SPECT for small-animal imaging: A method for addressing sampling completeness. IEEE Trans Nucl Sci. 2003 Oct;50(no 5):1575–1583. [Google Scholar]
- 16.Zeng GL, Gullberg GT. Helical SPECT using axially truncated data. IEEE Trans Nucl Sci. 1999 Dec;46(no 6):2111–2118. [Google Scholar]
- 17.Weng Y, Zeng GL, Gullberg GT. A reconstruction algorithm for helical cone-beam SPECT. IEEE Trans Nucl Sci. 1993 Aug;40(no 4):1092–1101. [Google Scholar]
- 18.Zeng GL, Gullberg GT, Christian PE, Gagnon G. Cone-beam iterative reconstruction of a segment of a long object. IEEE Trans Nucl Sci. 2002 Feb;49(no 1):37–41. [Google Scholar]
- 19.Smith BD. Image reconstruction from cone beam projections: Necessary and sufficient conditions and reconstruction methods. IEEE Trans Med Imag. 1985;MI-4(no 1):14–25. doi: 10.1109/TMI.1985.4307689. [DOI] [PubMed] [Google Scholar]
- 20.Jaszczak RJ, et al. Helical path, half-cone-beam acquisition for SPECT brain imaging. presented at the IEEE Nuclear Science Symp. and Medical Imaging Conf.; San Diego, CA. 2006. [Google Scholar]
- 21.Hoffman EJ, Cutler PD, Digby WM, Mazziotta JC. 3-D phantom to simulate cerebral blood flow and metabolic images for PET. IEEE Trans Nucl Sci. 1990 Apr;37(no 2):616–620. [Google Scholar]


