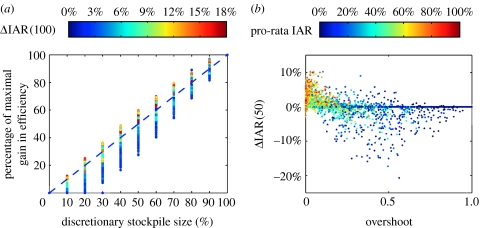
Figure 5.

(a) The percentage of maximal gain in efficiency (i.e. ΔIAR(100)) realized by a discretionary policy is an increasing function of its discretionary stockpile size d. This figure is generated as follows: for each stockpile size d, the quantity ρ(d)=ΔIAR(d)/ΔIAR(100) is computed for a 51 by 51 rectangular grid of the (R₀, c) plane. The colour of each point is colour-coded by the corresponding value of ΔIAR(100) using the same colour key in figure 2 (repeated here). The d–ρ(d) relation, which varies with (R₀, c), can be visualized by connecting points of the same colour. (b) To perform a multivariate sensitivity analysis on the 50% discretionary policy, we generate 5000 sets of model parameters in the ranges shown in table 1 using Latin hypercube sampling. Since inter-regional mixing is weak, the critical coverage $c_i^{*}$, i=1, …, K, are close to that when there is no inter-regional mixing, which are given by $(1-1/R_0^i)/VE$, i=1, …, K, where $R_0^i$ is the basic reproductive number in region i and $VE=1-(1-V{E}_{\text{S}})(1-V{E}_{\text{I}})$ is the overall vaccine efficacy. Therefore, given an allocation (α₁, …, α_K), the degree of overshoot can be accurately measured by $(1/cN){\sum }_{i=1}^K\text{max}(0,{\alpha }_{i}cN-c_i^{*}{N}_i)$ which is the proportion of stockpile misallocated due to overshooting when inter-regional mixing is zero. ΔIAR(50) drops sharply as the degree of overshoot increases. Each point of ΔIAR(50) is colour-coded by ΔIAR(0), which is the IAR under pro-rata. Overshoot is more likely when pro-rata IAR is low. That is, overshoot is more likely when the impact of the pandemic is relatively mild in the presence of pre-pandemic vaccination. ΔIAR(50) drops far below zero when there is overshoot and pro-rata IAR is below 50%.