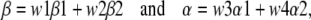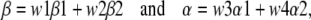SCHEME 1.

Here, the O1, O2, C1, and C2 in the model termed 2C-2O stand for long open, short open, long closed, and short closed states, respectively. In this model, the step C1↔C2 would behave as a single (closed) state C, and the step O1↔O2 as a single (open) state O. At equilibrium, we have p_c1β1 = p_o1α1 and p_c2β2 = p_o2α2. In other words, p_c1β1 + p_c2β2 = p_o1α1 + p_o2α2, where the p_ci and p_oi are the probabilities of the corresponding closed and open states (i = 1, 2), and β_i and α_i are the corresponding forward and backward rate constants between C_i and O_i (i = 1, 2). To convert the 2C-2O model into the C↔O (or C-O) model shown at right, we took p_cβ = p_c1β1 + p_c2β2 and p_oα = p_o1α1 + p_o2α2, where the p_c = p_c1 + p_c2 and p_o = p_o1 + p_o2 are total probabilities for open and closed states, and β and α are the equivalent forward and backward rate constants between C and O. For the equivalent C-O model, we got

(2)

where the weights w1 = p_c1/p_c, w2 = p_c2/p_c, w3 = p_o1/p_o, and w4 = p_o2/p_o, and w1 + w2 = 1 and w3 + w4 = 1. Finally, we got p_o = β/(α + β) and p_c = α/(α + β) in the C-O model, which gives p_o + p_c = 1.