FIG. 7.
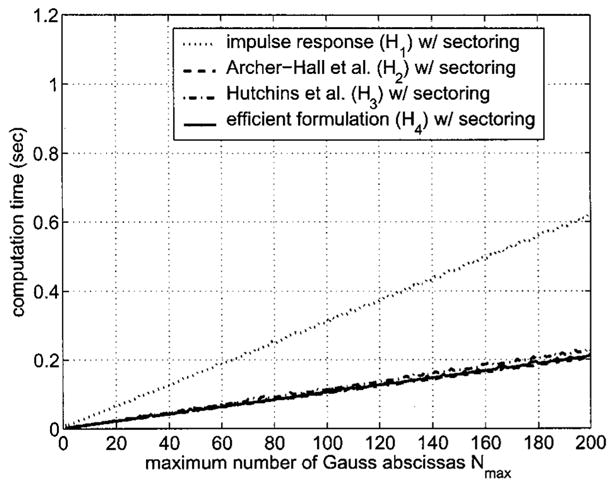
A comparison of computation times for beam patterns calculated with H1, H2, H3, and H4 combined with the grid sectoring approach defined in Eqs. (11) and (12) and plotted as a function of the maximum number of Gauss abscissas Nmax. Each beam pattern is computed for a piston radius a = 5λ on the same spatial grid as the reference in Fig. 3. The number of Gauss abscissas M in an individual sector ranges from 0.3Nmax to Nmax across the ns = 10 sectors indicated in Fig. 2. The axes are the same as in Fig. 5, so grid sectoring achieves roughly a factor of 2 reduction in the raw computation time for each integral formulation evaluated on this computational grid. Since grid sectoring reduces the computation time for each integral expression by nearly a factor of 2, H2, H3, and H4 are again approximately three times faster than the impulse response solution H1.
