Voltage-dependence of Ion Permeation in Cyclic GMP–gated Ion Channels Is Optimized for Cell Function in Rod and Cone Photoreceptors

Abstract

The kinetics of the photocurrent in both rod and cone retinal photoreceptors are independent of membrane voltage over the physiological range (−30 to −65 mV). This is surprising since the photocurrent time course is regulated by the influx of Ca²⁺ through cGMP-gated ion channels (CNG) and the force driving this flux changes with membrane voltage. To understand this paradigm, we measured Pf, the fraction of the cyclic nucleotide–gated current specifically carried by Ca²⁺ in intact, isolated photoreceptors. To measure Pf we activated CNG channels by suddenly increasing free 8-Br-cGMP in the cytoplasm of rods or cones loaded with a caged ester of the cyclic nucleotide. Simultaneous with the uncaging flash, we measured the cyclic nucleotide–dependent changes in membrane current and fluorescence of the Ca²⁺ binding dye, Fura-2, also loaded into the cells. We determined Pf under physiological solutions at various holding membrane voltages between −65 and −25 mV. Pf is larger in cones than in rods, but in both photoreceptor types its value is independent of membrane voltage over the range tested. This biophysical feature of the CNG channels offers a functional advantage since it insures that the kinetics of the phototransduction current are controlled by light, and not by membrane voltage. To explain our observation, we developed a rate theory model of ion permeation through CNG channels that assumes the existence of two ion binding sites within the permeation pore. To assign values to the kinetic rates in the model, we measured experimental I-V curves in membrane patches of rods and cones over the voltage range −90 to 90 mV in the presence of simple biionic solutions at different concentrations. We optimized the fit between simulated and experimental data. Model simulations describe well experimental photocurrents measured under physiological solutions in intact cones and are consistent with the voltage-independence of Pf, a feature that is optimized for the function of the channel in photoreceptors.

INTRODUCTION

Cyclic GMP–gated ion channels (CNG)* select Ca²⁺ over Na⁺ ions, but the extent of this selectivity differs among channels depending on the cell type in which they are naturally expressed (Haynes, 1995; Picones and Korenbrot, 1995; Finn et al., 1998; Seifert et al., 1999). The channels are permeable to Mg²⁺ and K⁺, alongside Ca²⁺ and Na⁺ (Nakatani and Yau, 1988; Colamartino et al., 1991; Zimmerman and Baylor, 1992). The specific features of ion selectivity are almost certainly correlated with the physiological role the channels play in each cell type. Among vertebrate photoreceptors the selectivity of Ca²⁺ over Na⁺, PCa/PNa, measured from reversal potential under biionic solution, is higher in cones than in rods (Frings et al., 1995; Picones and Korenbrot, 1995) and may be as much as five- to sevenfold higher at physiological cGMP concentrations (Hackos and Korenbrot, 1999). In intact cones and under normal physiological solutions, Ca²⁺ influx is ∼35% of the total inward current through CNG channels, but only ∼20% of that in rods (Ohyama et al., 2000).

Light regulates the cytoplasmic concentration of cGMP in rods and cones, which, in turn, controls the activity of CNG channels in their outer segment. Thus, the biophysical features of these channels determine the electrical properties of the light-dependent transduction current in photoreceptors. In intact photoreceptors and under normal ionic solutions, the photocurrent amplitude changes little with membrane voltage over the range between −30 and −65 mV (in rods: Bader et al., 1979; Baylor and Nunn, 1986; Hestrin and Korenbrot, 1987. In cones: Nicol et al., 1984; Miller and Korenbrot, 1993a). This biophysical feature has a profound functional consequence because light hyperpolarizes rods and cones over the same voltage range: from about −30 mV in darkness to −65 mV at the peak of the photoresponse (in rods: Schwartz, 1973. In cones: Baylor et al., 1974). This is surely a functional advantage since it insures that the amplitude of the phototransduction current is controlled by light and not by membrane voltage. This advantageous feature, however, is simply a consequence of the characteristic I-V curve of CNG channels under physiological solutions.

The I-V curve of the CNG channels helps explain the relative independence between photocurrent amplitude and photovoltage, but it cannot explain the effects of voltage on photocurrent kinetics. Under voltage-clamp, the time course of the photocurrent is independent of membrane voltages between −30 and −65 mV, again, an advantage from a cell physiology viewpoint. However, at depolarizing voltages ≥30 mV the photocurrent time course is slower than at the normal resting voltage of about −35 mV (in rods: Bader et al., 1979; Nicol et al., 1984; Baylor and Nunn, 1986. In cones: Nicol et al., 1984; Miller and Korenbrot, 1993b). This slowdown has been explained to arise from a decrease in the electromotive force (emf) that drives Ca²⁺ influx (Nicol et al., 1984; Baylor and Nunn, 1986; Miller and Korenbrot, 1994). Thus, as membrane depolarizes, Ca²⁺ emf and influx are lessened and the light-dependent decrease in cytoplasmic Ca²⁺ associated with the photoresponse (Gray-Keller and Detwiler, 1994; Younger et al., 1996) become proportionally smaller. Since photocurrent kinetics is regulated by the level of cytoplasmic Ca²⁺ (for review see Pugh and Lamb, 2000), then a smaller change in cytoplasmic Ca²⁺ slows down the transduction current. The problem with this explanation, however, is that Ca²⁺ emf also changes as the voltage hyperpolarizes and, therefore, the hypothesis anticipates that photocurrent kinetics should also change between −30 and −65 mV. An additional mechanism must exist to explain the lack of voltage effect on photocurrent kinetics over the photovoltage range. To understand what this additional process might be, we investigated in intact rods and cones the effects of membrane voltage on the fraction of the cGMP-gated current carried by Ca²⁺, a quantity we denominate Pf (Ohyama et al., 2000).

We have found that Pf is voltage-independent over the photovoltage range, a mechanism that helps explain the constancy of photocurrent kinetics at all photovoltages. This fact, however, is inconsistent with simple electrodiffusion theory and we have used rate theory to understand its mechanisms. The theoretical framework we have used is similar to that originally developed for rod CNG currents by Wells and Tanaka (1997). We have performed an analysis of ion permeation that has allowed us to compare the mechanisms of Ca²⁺ permeation in rod and cone CNG. This theoretical framework has allowed us to explain the voltage independence of Pf as well as to develop a mechanistic description of the I-V relationship of cone photocurrent in intact cells.

MATERIALS AND METHODS

Materials

We obtained striped bass fish (Morone saxitilis) from Professional Aquaculture Services and maintained them in the laboratory for up to 6 wk under 10:14 h dark:light cycles. We received larval stage tiger salamanders (Ambystoma tigrinum) from Charles Sullivan and maintained them in an aquarium at 6°C under 12:12 h dark:light cycles. The UCSF Committee on Animal Research approved protocols of animal care and euthanasia.

Caged 8-Br-cGMP (8-Bromoguanosine 3′, 5′-cyclic monophosphate, 4,5-dimethoxy-2-nitrobenzyl ester, dihydrate, axial isomer) was a gift of V. Hagen (Forschungs Institut for Molekulare Pharmacologie, Berlin, Germany), who has described its synthesis (Hagen et al., 1998). Fura-2 was purchased from TefLabs. Enzymes for tissue dissociation were obtained from Worthington Biochemical. All other chemicals were from Sigma-Aldrich.

Photoreceptor Isolation

Under infrared illumination and with the aid of a TV camera and monitor, we separated retinas from dark-adapted eyes and isolated photoreceptors as detailed elsewhere (Miller and Korenbrot, 1993b, 1994). Single cones were dissociated by mechanical trituration of fish retinas briefly treated with collagenase and hyaluronidase. Detached rod outer segments (dROS) were obtained by chopping tiger salamander retinas with a sharp blade. Photoreceptors were isolated in a Ringer's solution (Table I) containing pyruvate (5 mM) instead of glucose. The suspension of dissociated cells (∼250 μl) was transferred onto a recording chamber held on a microscope stage. The bottom of the recording chamber was a Concanavalin A–coated glass coverslip and cells attached firmly to this substrate. After 10 min, the pyruvate-Ringer's was replaced with normal Ringer's, which was then intermittently exchanged for the duration of the experiment.

TABLE I.

Composition of Physiological Solutions

	Striped bass		Tiger salamander
	Extracellular Ringer's	Electrode filling solution	Extracellular Ringer's	Electrode filling solution
NaCl (mM)	136	9	100	–
KCl (mM)	2.5	10	2	30
NaHCO3 (mM)	5	–	5	–
NaH2PO4 (mM)	1	–	1	–
Kgluconate (mM)	–	105	–	69
Kaspartate (mM)	–	20	–	20
CaCl2 (mM)	1		1
MgCl2 (mM)	1	0.5	1	0.5
Glucose (mM)	10		10
MEM vitamins and amino acids	1×	–	1×	–
HEPES (mM)	10		10
MOPS (mM)		10		15
pH	7.5	7.25	7.5	7.25
Osmotic pressure (mOsM)	310	305	227	226

Recording Currents in Detached Membrane Patches

Under microscopic observation using visible light, we obtained cytoplasmic-out membrane patches with tight-seal electrodes sealed onto the sides of rod or cone outer segments. Complete details can be found elsewhere (Picones and Korenbrot, 1992). We produced electrodes from aluminosilicate glass (Corning 1724) (1.5 × 1.0 mm OD × ID) and, regardless of the species under investigation, we filled them with a solution composed of (in mM): NaCl (157), EGTA (1), EDTA (1), HEPES (10), osmotic pressure 305 mOsM. Free Ca²⁺ concentration in this solution was ≤10⁻¹⁰ M; total Na⁺ concentration was 167 mM because NaOH was used to adjust to pH 7.5. We refer to this as our standard solution. We measured membrane currents under voltage clamp at room temperature with a patch-clamp amplifier (Axopatch 200A; Axon Instruments, Inc.). Membrane capacitance was compensated, but series resistance was not. Analogue signals were low-pass filtered below 1 kHz with an 8-pole Bessel filter (Frequency Devices) and digitized on line at 2.5 kHz (FastLab; Indec). To generate I-V curves, membrane voltage was first stepped to −100 mV for 50 ms and then ramped linearly between −100 and 100 mV at a rate of 228 mV/s. Ramps were swept on four successive trials with a 1.2-s interval between trials; currents were signal averaged over the four trials. Between voltage ramp trials, membrane voltage was held at 0 mV. As is usual, outward currents are positive and the extracellular membrane surface is defined as ground.

We delivered test solutions onto the cytoplasmic (bath) surface of the membrane patch through a 100-μm diameter glass capillary placed within 100 μm of the electrode tip (Picones and Korenbrot, 1992). We selected from among four possible test solutions depending on the objective of the experiment: (a) the standard solution; (b) the standard solution with 1 mM cGMP; (c) the standard solution containing 1 mM cGMP and additional CaCl₂ or MgCl₂ in concentrations sufficient to yield the free concentrations listed in the text; or (d) a modified standard solution in which Na⁺ was replaced by K⁺ at various concentrations. Total Na⁺ concentration in the Ca²⁺- or Mg²⁺-containing solution was 162 mM, since NaOH was used to bring final pH to 7.5. Because we used a 1 M KCl agar bridge with the bath reference electrode, changes in bathing solutions caused changes in junction potential ≤1 mV.

Rate theory predicts current through open channels. To convert macroscopic patch currents, I, into single channel currents, i, the number of channels present in the patch (N) and their probability of opening (Po) must be known (I = iNPo). We have previously ascertained the under symmetric Na⁺ solutions (167 mM), and with 1 mM cGMP the single channel conductance of bass cones is 26 pS at 10 KHz and the probability of channel opening is 0.83 (Picones and Korenbrot, 1994). To determine N in each patch studied, we first measured currents in the presence of symmetric Na⁺ (167 mM) and 1 mM cGMP and divided by the single channel current computed from the parameters listed above. We only analyzed currents activated by saturating cGMP concentrations, because under these conditions the addition of Ca²⁺ or Mg²⁺ changes open channel conductance but not probability of opening (Colamartino et al., 1991). At nonsaturating cGMP concentrations Ca²⁺ and Mg²⁺ affect both open channel conductance and probability of opening (Colamartino et al., 1991).

Fraction of cGMP-gated Current Carried by Ca²⁺, Pf

We have detailed the theory and the method of this measurement before (Ohyama et al., 2000). In brief, under a defined set of experimental conditions, the membrane current and cytoplasmic Ca²⁺ concentration are simultaneously measured in intact photoreceptors loaded with Fura-2 (2 mM) and caged 8-Br-cGMP (50 μM). CNG channels are suddenly activated by flash photolysis of the caged compound. If Ca²⁺ ions are the only carriers of the current flowing through the activated channels, then the total change in cytoplasmic Ca²⁺ is the integral of the current change. If Ca²⁺ ions are only a fraction of the charge carriers, then the change in total Ca²⁺ is less than the current integral and the exact value of the fraction Pf can be computed. To assure that the total change in Ca²⁺ is measured, not confounded by intracellular buffering or sequestration or by active transport, Pf must be measured in the presence of high Fura-2 concentrations. Because of this high concentration, the initial changes in Fura-2 fluorescence reflect the equilibrium conversion of Ca²⁺-free to Ca²⁺-bound states of the dye, whereas the effective free Ca²⁺ concentration remains nearly zero (<10⁻¹⁰ M).

Under video-microscopic observation using infrared light (850 ± 40 nm), we attached tight-seal electrodes to the inner segment of single cones or dROS. Electrodes were produced from aluminosilicate glass (Corning 1724, 1.5 × 1.0 mm OD × ID). We measured membrane currents under voltage clamp at room temperature with a patch clamp amplifier (Axopatch 1D; Axon Instruments, Inc.) in the whole-cell mode. Analogue signals were low pass filtered below 200 Hz with an 8-pole Bessel filter (Kronh-Hite) and were then digitized on line at 1 KHz (FastLab; Indec). Solutions used to fill tight-seal electrodes are listed in Table I. Salt solutions were first passed over a Chelex-100 resin column (Bio-Rad Laboratories) to remove all multivalent cations and MgCl₂ was then added. Fura-2 and caged 8-Br-cGMP (from a stock 25 mM in DMSO) were added to the solutions immediately before use. Because caged 8-Br-cGMP spontaneously hydrolyzes over time (Hagen et al., 1998), the electrode-filling solutions were kept in darkness and discarded after ∼3 h. To measure cGMP-gated currents carried exclusively by Ca²⁺, the permeant cations Na⁺ and Mg²⁺ were replaced by the impermeant cations choline⁺ or tetramethylamonium⁺ (Hodgkin et al., 1985).

Fluorescence in single photoreceptors was excited at 380 nm with light delivered through the microscope's objective. Fluorescence emitted in the 410–600 nm range was collected with a specially designed micro-objective and counted in 50-ms bins with a photomultiplier tube operated in photon counting mode (Ohyama et al., 2000). Fluorescence intensity was calibrated by measuring at the end of each experiment the fluorescence of individual fluorescent beads added to the recording chamber and excited identically to the cells (Fluoresbrite™ carboxy BB 4.1 ± 0.2 μm microspheres; Polyscience, Inc.). Fluorescence intensity of both cells and beads was corrected by subtracting the signal measured from each in their absence and due to leakage of light between excitation and emission filter sets (cross talk). In each experiment, we averaged the fluorescence of ten different beads (in units of counts per 50-ms bin) and defined this intensity as one bead unit (b.u.). Cell fluorescence was expressed in b.u. by dividing the cell's emission intensity by the b.u. measured in the same experiment.

To uncage 8-Br-cGMP, we used a Xenon flashlamp to deliver 170-μs flashes of ∼200 J (Chadwick-Helmuth Co.). Uncaging light was <400 nm and was focused onto the isolated cells through the microscope's objective using epi-illumination. Uncaging light flashes were delivered over the entire detached rod outer segments, but were restricted to the cone outer segment alone with the use of an adjustable aperture.

RESULTS

In single cones from striped bass or dROS from tiger salamander we measured the fraction of the cGMP-gated current carried by Ca²⁺ at various membrane voltages. To this end, we simultaneously measured voltage-clamped currents and cell fluorescence from isolated photoreceptors loaded with Fura-2 and caged 8-Br-cGMP. Throughout the measurement we continuously monitored the holding current at −35 mV. The amplitude of this current is a measure of the electrical stability of the recording and the completeness of diffusion exchange between electrode lumen and cell's cytoplasm. The electrode-filling solution lacked nucleotides triphosphate and, therefore, photoreceptors could not sustain endogenous cGMP synthesis (Hestrin and Korenbrot, 1987; Rispoli et al., 1993). Thus, in single cones the holding current, which was near zero immediately after achieving whole-cell mode, slowly (over a minute or two) drifted to a steady outward value. The drift reflects the continuing diffusional exchange between electrode lumen and cell cytoplasm, and the associated loss of CNG channel activity as cGMP is lost from the outer segment. In the steady-state, the net current is outward because the outer segment channels are inactive and current flows through the voltage-gated K⁺ channels in the inner segment (Maricq and Korenbrot, 1988, 1990; Barnes and Hille, 1989). In dROS, in contrast, the current was inward immediately after achieving whole cell mode and then it slowly drifted toward its near zero amplitude at equilibrium. This behavior follows from the fact that CNG channels are the only channels present in the membrane of dROS (Baylor and Nunn, 1986; Hestrin and Korenbrot, 1987).

Pf Dependence on Membrane Voltage in Single Cones

We measured data in single cones beginning no less than 3 min after going into whole cell mode and only while Ihold at −35 mV was within 20% of the value measured at 3 min. The mean holding current at −35 mV was 23.5 ± 13.1 pA (n = 43). Voltage was stepped to the test value and after 200 ms we uncaged 8-Br-cGMP with a bright light flash. Uncaging activated the CNG channels in the outer segment, causing an inward current at all voltages tested. The current rapidly reached to a peak and then declined with an exponential time course (Fig. 1, top). The kinetics of current decline from its peak value are principally determined by the rate of binding of the freed nucleotide to intracellular buffering sites (Ohyama et al., 2000). The cGMP-gated current is carried in part by Ca²⁺, and the entering Ca²⁺ binds to cytoplasmic Fura-2 causing the decrease in cell fluorescence at 380 nm simultaneous with the current change (Fig. 1, middle). The integral of the current change is a measure of the total charge entering the cone outer segment, whereas the fluorescence change specifically measures the total amount of Ca²⁺ entering the outer segment, provided all the entering Ca²⁺ is bound by Fura-2 and none is lost either to competing intracellular buffers or to sequestration by other compartments. In photoreceptors this necessary condition holds for 5–10 s following the uncaging flash (Ohyama et al., 2000). Over this limited time period the integral of the current and the change in fluorescence have the same time course (Fig. 1, middle). We determined the value of f, the ratio of the change in fluorescence to the integral of the current change only over this restricted time span.

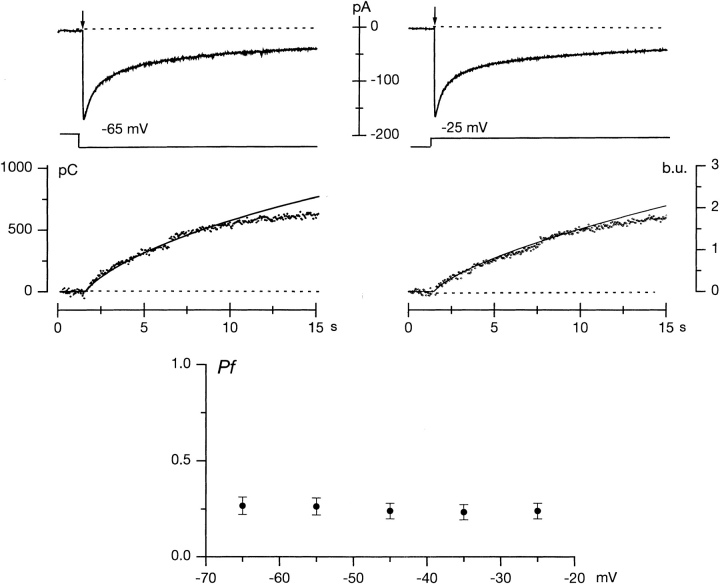
Figure 1.

Voltage dependence of Pf in a single cone isolated from striped bass retina. Data shown were measured in the same cell in successive trials at either −55 mV or −25 mV membrane voltage. Intracellular 8-Br-cGMP generated through flash photolysis of a caged compound (flash delivery indicated by arrow) activated an inward current (top) and caused a decrease in fluorescence excited at 380 nm (illustrated with symbols as an upward change in the middle panels. Cell was held at −35 mV and stepped to the test voltage 200 ms after beginning data acquisition. In the middle panels, the continuous line superimposed on the fluorescence change is the time integral of the membrane current (in units of picocoulombs, pC) adjusted in amplitude to best fit the fluorescence signal. The bottom panel illustrates the mean (± SD) value of Pf measured at various membrane voltages.

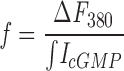We repeatedly measured f in the same cone at test voltages between −65 and −25 mV, in 10 mV steps. The cell was held at −35 mV between tests. The number of repeat tests in any given cell was limited by the lifetime of the electrical recording and was between two and five. We repeated measurements at 3–4-min intervals, a time sufficiently long for cells to recuperate as evidenced by the recovery of both holding current and fluorescence to their starting values. We measured f in a total of 43 different cones, and the f value at each voltage is the average of between four and nine different cells.

We also measured fmax, the value of f when Ca²⁺ is the exclusive current carrier in CNG channels (see materials and methods). fmax was voltage-independent and its average value was 0.0098 ± 0.0014 b.u./pC (n = 9, range 0.008–0.0125). Pf is simply f/fmax. We found that in these single cones mean Pf was 0.33 ± 0.08 at −35 mV (n = 43). The mean Pf value was essentially independent of membrane voltage between −65 and −35 mV (Fig. 1, bottom).

Pf Dependence on Membrane Voltage in Rods

We measured data in dROS starting at least 4.5 min after going into whole cell mode and while Ihold at −35 mV was between 0 and −12 pA; mean Ihold = −6.1 ± 3.1 pA (n = 39). In rods, just as in cones, uncaging 8-Br-cGMP caused an inward current due to activation of CNG channels with a time course defined by the kinetics of binding of the free nucleotide to intracellular sites (Fig. 2, top). The Ca²⁺ influx associated with channel activation caused a decrease in the 380 nm fluorescence of cytoplasmic Fura-2 (Fig. 2, middle). The integral of the current change could be matched to the change of fluorescence for 5–15 s following the uncaging flash (Fig. 2, middle).

Figure 2.

Voltage dependence of Pf in a detached rod outer segment isolated from tiger salamander retina. Data shown were measured in the same cell in successive trials at either −65 mV or −25 mV membrane voltage. Intracellular 8-Br-cGMP generated through flash photolysis of a caged compound (flash delivery indicated by arrow) activated inward membrane currents (top) and a decrease in fluorescence (illustrated with symbols as an upward change in the middle panels. In the middle panels, the continuous line superimposed on the fluorescence change is the time integral of the current adjusted in amplitude to best fit the fluorescence signal. The bottom panel illustrates the mean (± SD) value of Pf measured at various membrane voltages.

We repeatedly measured f in the same dROS at test voltages between −65 and −25 mV in 10 mV steps. The cell was held at −35 mV between tests. In any given cell we measured f at 3 to 5 different voltages, waiting 3 to 4 min between repeats. This repeat interval was sufficient to allow cells to recuperate to their starting state, as evidenced by the recovery of the initial values of both holding current and fluorescence. We measured f in a total of 39 different rods, and the f value at each voltage is the average of between 5 and 10 different cells. In rods, as in cones, fmax was voltage-independent and its average value was 0.0112 ± 0.0019 b.u./pC (n = 8, range 0.0101–0.0130). The mean Pf value at −35 mV was 0.26 ± 0.03 (n = 10). The mean Pf value was essentially independent of membrane voltage between −65 and −35 mV (Fig. 2, bottom).

Adjusting a Rate Theory Model to Experimental I-V Functions in Cone CNG Channels

The independence of Pf from membrane voltage in rod and cone CNG is not expected from simple electrodiffusion theory. To understand our experimental results, we developed a model of the interaction between permeant cations and CNG channels based on theory of rate processes as applied to the diffusion of ions through channel pores (Zwolinski et al., 1949; Hille, 1975). In the we present in brief the mathematical details of the model as we have applied it. We presume that every permeant ion can bind to two specific sites in the permeation pore; the sites are separated from each other and the membrane surfaces by energy barriers (three barriers, two wells) (see Fig. 5). Ions flow by jumping from site to site driven by differences in free energy between the sites and biased by the energy of applied membrane voltage and the energy that arises from the interaction between the jumping ions and other ion that may already be bound to their permeation site. The amplitude of the barriers and wells is given in units of RT and their location in units of electrical membrane thickness. This electrical thickness is the thickness of the membrane over which the applied voltage drops; its value is zero at the extracellular surface and one at the intracellular surface. The task is to define the rates at which ions jumping between sites and to predict I-V curves similar to those experimentally observed.

Figure 5.

Diagram of the energy profile of Ca²⁺ and Na⁺ permeation through CNG ion channels of rods and cones. The rate model hypothesizes there exist two binding sites (energy wells G2 and G3), separated from each other and the cytoplasmic and extracellular surfaces by energy barriers (G12, G23, and G34). Each of the energy minima and maxima are located at defined positions along the electrical thickness of the membrane (D12, D2, D23, D3, D34) between 0 (extracellular membrane surface) and 1 (cytoplasmic). Amplitudes of wells and peaks are computed in units of RT. The absolute values of peaks and wells are somewhat arbitrary since they depend on the frequency factor value selected (see text and ). However, the relative thermodynamic differences between ions in a given channel, or between channels for a given ion are informative since these differences will be the same regardless of the frequency factor value.

To define the features of energy wells and barriers consistent with experimental data we used our modified version of Ajuste (Alvarez et al., 1992), a software program (shared by Dr. O. Alvarez, Universidad de Chile, Santiago, Chile) that uses nonlinear, least-square minimization algorithms to optimize the fit between simulated and experimental data. A problem, however, is that the number of adjustable variables in the theoretical model is large and, even with optimization protocols, reasonable fits between theory and results can be obtained with more than one set of variables. To constrain the model and reduce the number of adjustable variables we fit data measured in photoreceptor membrane patches under simple ionic solutions consisting of ion pairs (Na⁺/Na⁺, Na⁺/Na⁺+Ca²⁺, Na⁺/Na⁺+Mg²⁺, or Na⁺/K⁺) tested at several different concentrations. Further, we demanded that all data measured in the same patch be fit with the same set of variables at all ion concentrations tested. Because limits on the lifetime of membrane patches kept us from testing each and every one of all the ionic solutions on the same patch, all experiments were conducted with similar Na⁺ solutions on the extracellular membrane surface. We further constrained the model by demanding that the Na⁺ energy barriers be identical in each and every membrane patch analyzed (a total of 10 patches), regardless of the identity of the other ions present.

We measured I-V curves of cGMP-gated currents between −90 and 90 mV in membrane patches detached from cone outer segments. We activated macroscopic currents with 1 mM cGMP and computed single channel currents from the macroscopic data (see materials and methods). Fig. 3 illustrates data measured in 3 different cone membrane patches under various ionic solutions. In one patch (Fig. 3 A) currents were measured under symmetric Na⁺ solutions (162/167 mM in/out) with varying concentrations of Ca²⁺ (0–15 mM) added to the bath surface. I-V curves were nearly linear in the absence of Ca²⁺ and changed in its presence to reveal the known voltage-dependent block of open channels (Haynes, 1995; Picones and Korenbrot, 1995). In a second patch (Fig. 3 B) currents were measured under the symmetric Na⁺ solutions with varying concentrations of Mg²⁺ (0–15 mM) added to the cytoplasmic surface. Mg²⁺ ions, just as Ca²⁺, permeate through the channels and cause a voltage-dependent block. In a third patch (Fig. 3 C) we measured currents under bionic solutions with a fixed Na⁺ concentration in the pipette surface (167 mM) and varying K⁺ concentrations (50, 162, and 500 mM) on the bath surface. The channels discriminate poorly between the two cations and I-V curves changed little in shape, but shifted as the equilibrium potential changed.

Figure 3.

I-V curves of cGMP-dependent currents measured in membrane patches detached from the outer segment of bass single cones. Data in each panel were measured in different cytoplasmic-out patches, but currents within each panel were all collected from the same patch. Currents were activated by linear voltage ramps (228 mV/s) between −90 and 90 mV in the presence of 1 mM cGMP, a concentration sufficient to maximally activate CNG channels. cGMP-dependent currents are shown as continuous lines and were obtained after subtracting currents activated by the same voltage ramps in the same patch, but in the absence of cGMP. (A) Currents measured under symmetric Na⁺ solution in the presence of varying intracellular Ca²⁺ concentrations between 0 and 15 mM, as labeled. (B) Currents measured under symmetric Na⁺ and in the presence of varying intracellular Mg²⁺ concentrations between 0 and 15 mM, as labeled. (C) Biionic currents measured in the presence of constant extracellular Na⁺ and varying intracellular K⁺, as labeled. Superimposed on the experimental currents and shown as filled circles (•) are results of simulations computed by optimally fitting the experimental data with the predictions of a rate theory model that assumes two ion binding sites exist within the CNG channel permeation path.

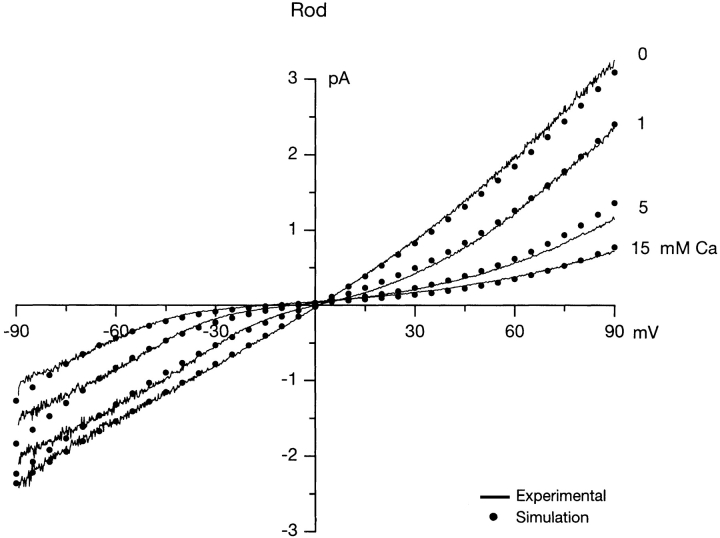
We also measured currents in membrane patches detached from rod outer segments and compared results with those measured in cones. We limited our exploration in rod patches to measurements in the presence of Ca²⁺, since Wells and Tanaka (1997) have previously analyzed rod currents measured in the presence of Ca²⁺, Mg²⁺, and K⁺ and our results and conclusions fully reproduce theirs. In the same membrane patch and in the presence of 1 mM cGMP, we first measured currents under symmetric Na⁺ solutions (162/167 in/out in mM) and then in solutions with 1, 5, and 15 mM Ca²⁺ added to the solution bathing the cytoplasmic membrane surface. As shown in Fig. 4, in the absence of Ca²⁺ the I-V curves are slightly asymmetric, possibly because of small voltage effects on open channel lifetime (Benndorf et al., 1999). As cytoplasmic Ca²⁺ concentration increases, the I-V curves change in shape, demonstrating voltage-dependent block of the open channel by the divalent cation. The reversal potential shifts as expected from the fact that Ca²⁺ is more permeable than Na⁺ (Picones and Korenbrot, 1995).

Figure 4.

I-V curves of cGMP-dependent currents measured in a membrane patch detached from a tiger salamander rod outer segment. The continuous lines are experimental currents activated by linear voltage ramps in the presence of 1 mM cGMP. Currents were repeatedly measured in the same patch in the presence of symmetric Na⁺ solutions and varying cytoplasmic Ca²⁺ concentrations between 0 and 15 mM, as labeled. Superimposed on the experimental currents and shown as filled circles (•) are results of simulations computed by optimally fitting the experimental data with the predictions of a rate theory model that assumes two ion binding sites exist within the CNG channel permeation path.

Using rate theory, we simulated I-V curves to fit our experimental results in cone and rod CNG. Simulated data in Figs. 3 and 4 are illustrated as symbols superimposed on the experimental results. The simulated data were computed under the constraints detailed above and, in addition, we demanded that the energetics of Na⁺ diffusion be the same in rod and cone channels. The fit between simulated and experimental data is reasonable, in particular considering the strong constraints we imposed on the adjustable variables (see above). Table II presents, for each ion, the values of the forward and reverse rates for transitions at 0 mV when the channel is otherwise unoccupied. Simulated data computed with the thermodynamic values listed in Table II fit experimental data measured in eight additional membrane patches, two each tested under the same Ca²⁺, Mg²⁺, and K⁺ solutions, with an accuracy similar to that shown in Figs. 3 and 4.

TABLE II.

Ion-specific Rate Constants for Transitions across the Permeation Pathway in cGMP-gated Ion Channels

	Single cone				Rod
	Na+	Ca2+	Mg2+	K+	Na+	Ca2+
	s−1	s−1	s−1	s−1	s−1	s−1
k1	3.79 × 1010	5.75 × 1010	1.75 × 1011	6.33 × 109	3.79 × 1010	3.65 × 1010
k2	2.11 × 108	3.90 × 105	1.89 × 106	9.75 × 106	2.11 × 108	1.97 × 105
k3	2.09 × 107	6.28 × 109	4.99 × 105	5.73 × 106	2.09 × 107	4.52 × 107
k4	3.00 × 107	1.08 × 1010	3.47 × 105	5.84 × 107	3.00 × 107	3.24 × 107
k5	6.63 × 108	2.53 × 105	1.84 × 105	1.27 × 109	6.63 × 108	2.20 × 105
k6	8.30 × 1010	6.41 × 1010	2.46 × 1010	8.11 × 1010	8.30 × 1010	2.93 × 1010

Using the definitions in the Scheme I below, these are the values of rate constants (in s⁻¹) for each ion at 0 mV membrane voltage and when transitions occur in the absence of any other ion in the channel.

The values of the rate constants in Table II can be represented graphically by depicting energy barriers and wells inferred from these rates. The form of this graphical representation, however, absolutely depends on the duration of the elementary frequency event assumed in the calculations. In ion permeation studies (Hille, 1975), this frequency event has historically been assigned the value of kT/h ∼6 × 10¹². In an editorial policy (Andersen, 1999b), this Journal has pointed out that this commonly used value is theoretically inadequate and requests that graphical representations use more reasonable, though equally arbitrary, values between 10⁸ and 10¹⁰ s⁻¹. The size and location of energy barriers inferred from data in Figs. 3 and 4, assuming the frequency factor is 10¹⁰, are illustrated in Fig. 5. The “peaks” all have negative values because of the value of the frequency factor. Previous comparable studies (Wells and Tanaka, 1997) have barriers with positive values because they used the value of kT/h as the frequency factor; theirs and our rate constants, however, are similar in value. What is important about the graphical representation is not the absolute energy values, but what can be understood from the relative amplitude of barriers and wells (Andersen, 1999b).

Differences in the Energy Profiles of Rod and Cone CNG Channels

The interaction and permeation of divalent cations differs between CNG channels of rods and cones (Frings et al., 1995; Haynes, 1995; Picones and Korenbrot, 1995). The thermodynamic features of rod and cone channels inferred from our data (Table II) are illustrated as a diagram in Fig. 5. Shown are the location (in units of electrical membrane thickness) and size (in RT units) of the energy profiles for Na⁺ and Ca²⁺ in each channel. By definition, the profile for Na⁺ is the same in both channels. In both rods and cones the Ca²⁺ energy profiles have deeper wells than the Na⁺ profile, indicating the interaction between Ca²⁺ and the channels is favored over that between Na⁺ and the channels. This, of course, is manifested by the higher selectivity for Ca²⁺ over Na⁺ in both channel types. The Ca²⁺ energy profiles differ in rods and cones allowing a mechanistic view of the Ca²⁺ permeation differences between the channel types. The height of the outermost barriers and the depth of both wells are rather similar. This indicates that in rods and cones, Ca²⁺ interacts with the internal and external binding sites with nearly the same characteristics. This is consistent with the fact that in both rods and cones current block by intracellular Ca²⁺ is described by a single Langmuir absorption isotherm with the same value for the concentration that half-blocks the open channel conductance, ∼1 mM (Picones and Korenbrot, 1995). On the other hand, the internal barrier (G23) is much smaller in cones than in rods, indicating that Ca²⁺ can jump between internal binding sites more readily in cones than in rods. This feature explains why the Pf value of cone CNG channels is higher than that of rod channels.

Simulation of Cone Photocurrent in the Intact Cell and the Effects of Voltage on Pf

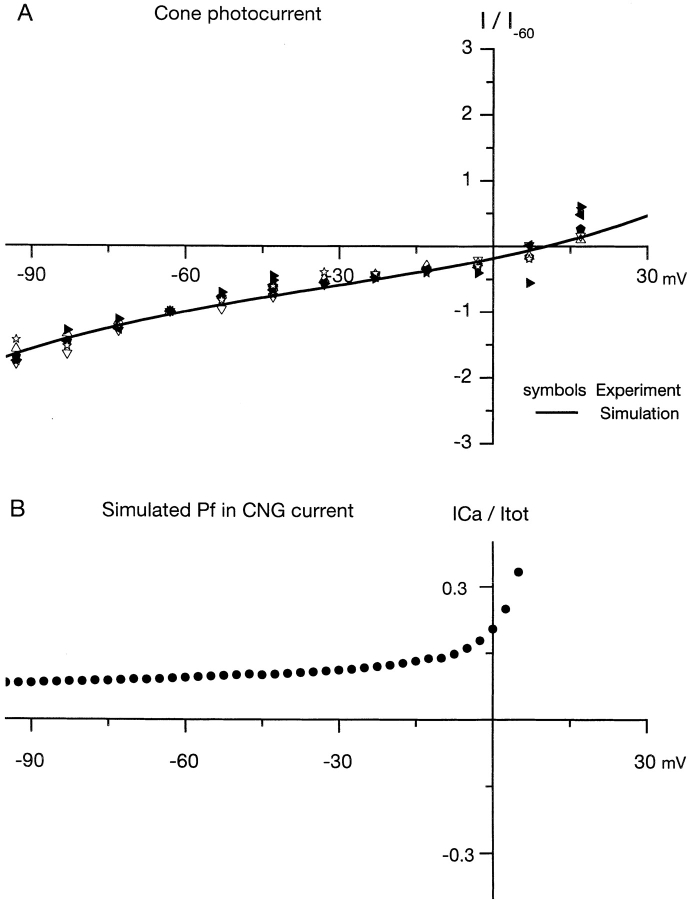
To further explore the adequacy of the rate model to understand ion permeation in cone CNG, we used the parameters assessed under simple ionic solutions to simulate I-V curves expected under complex physiological solutions. We extended the computational model to include four permeant ions (Na⁺, K⁺, Ca²⁺, and Mg²⁺) at the concentrations listed in Table I and with the rate parameters listed in Table II. Fig. 6 A illustrates a computed I-V curve for a single cone CNG channel superimposed on experimental data. The experimental data are I-V curves of the macroscopic peak photocurrent measured in single cones under the ionic solutions listed in Table I (data from Miller and Korenbrot, 1993a). We could not compute photocurrent single channel data because we cannot assess the number of channels active in the intact cells. To compare experimental data among different cells and also to compare with simulated results, we normalized the I-V curves by dividing, for each cell, the current amplitude at each voltage by the amplitude measured at −60 mV. In Fig. 6 A, normalized experimental photocurrents from six different cells are presented as symbols and the simulated curve as a continuous line. There is good match between the two sets of results (average square root of sum of square differences between data and simulation is 0.1). The reversal potentials for the currents are essentially the same: 9.9 mV for simulation and 9.8 ± 2.4 mV for experiment (n = 6, range 7.3–12.5 mV). The computational ability to describe the photocurrent is particularly remarkable since simulated data were computed from a single set of values derived from fits between theory and experiments under simple ion solutions in membrane parches, whereas the experimental photocurrent comes from many different intact cells under complex ion solutions. Thus, the rate model offers a reasonable representation of the mechanisms of ion interaction in CNG channels both under simple and complex ion mixtures.

Figure 6.

(A) I-V curves of photocurrents measured in intact single cones under physiological solutions (data from Miller and Korenbrot, 1993a). Peak photocurrent amplitude was measured at dark holding voltages between −95 mV and 25 mV (in 10 mV steps) in six different cells, each illustrated by a different symbol. To compare among photoreceptors, the photocurrent peak amplitude in each cell was normalized by dividing the amplitude at each voltage by that measured at −60 mV in the same cell. The continuous line is the I-V curve generated by a simulation based on the predictions of a rate model of permeation with the parameters presented under Table II. The simulated data was normalized just as described for the experimental data, but no attempt was otherwise made to fit simulated to experimental results. The superimposition of the two sets of independent data is a measure of the adequacy of the model proposed. B illustrates simulated predictions of the value of Pf and its voltage dependence made by the same model.

We used the rate model to understand the mechanisms of Pf dependence on voltage. Again using the values in Tables I and II, we computed the value of Pf for cone CNG as a function of voltage. Results of the computation are illustrated in Fig. 6 B. Indeed, the model anticipates the experimental finding: Pf is essentially voltage-independent over the range between −35 and −65 mV. However, the model is not fully accurate because it predicts a Pf value around 0.15, rather then the observed 0.35 (Fig. 1). This failure is evidence that the model is just a reasonable approximation to reality. Despite this shortcoming, it seems clear that the functionally advantageous fact that Pf is invariant with voltage over the physiological range can be explained by the physics of the interaction between ions and CNG channels, without the need to invoke effects of voltage on gating or channel structure.

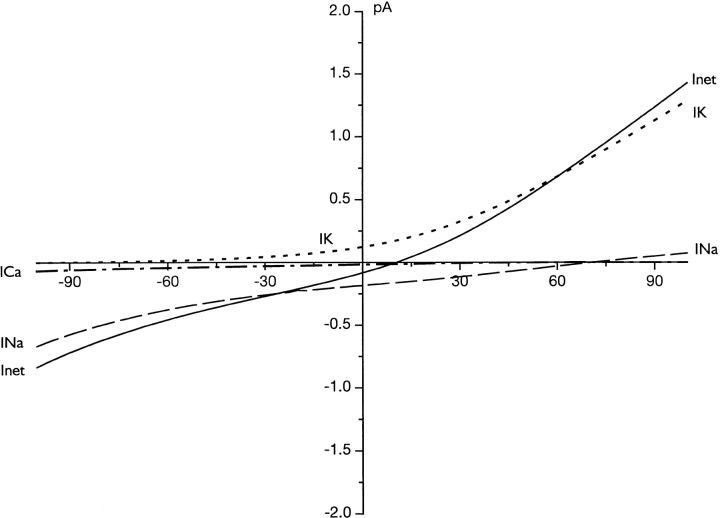
The rate model offers us the opportunity to analyze the specific contribution of each of the permeant cations to the CNG-gated current in cones. Fig. 7 illustrates I-V curve for Na⁺, K⁺, and Ca²⁺ currents computed separately. Inspection of the results indicate that, as expected, the dominant charge carrier of inward current is Na⁺, whereas K⁺ is the dominant carrier of outward current. Importantly, Mg²⁺ ions, although not very permeable, carry nearly as much inward current as Ca²⁺ because of their high concentration in both intra- and extracellular space.

Figure 7.

Simulated I-V curves of the net photocurrent and its specific ionic constituents in a single cone photoreceptor under physiological solutions. Shown are the results of computations based on the rate permeation model specified in the text. The specific current carried by each permeant cations is identified by a unique graphic line, as labeled. The lower, right panel illustrates the same simulated data with higher resolution over the range between −65 and −30 mV. This is the voltage range over which the cell can be expected to operate under physiological conditions.

DISCUSSION

Photoreceptor CNG ion channels are an elegant example of evolutionary progression in which biophysical details of function have been optimized to achieve the cell's purpose. Here, we report that the fraction of the channel's current carried by Ca²⁺, Pf, is constant and independent of voltage over the range of the photovoltage. This surprising feature is contrary to the expectations of simple electrodiffusion theory, but can be understood through a more complex view of ion permeation, such as that offered by rate theory. Whatever its precise mechanisms, the independence between Pf and photovoltage is important because it provides a mechanism to help explain the fact that in both rods and cones photocurrent kinetics are independent of photovoltage.

Cytoplasmic free Ca²⁺ in rod and cone outer segments is maintained by the dynamic balance between Ca²⁺ influx via the CNG channels and its efflux via Na⁺/Ca²⁺,K⁺ exchangers (Yau and Nakatani, 1985; Miller and Korenbrot, 1987). The light-dependent closure of CNG channels, in the presence of continuing Ca²⁺ efflux causes a light-dependent decrease of cytoplasmic Ca²⁺ (Gray-Keller and Detwiler, 1994; Younger et al., 1996) that, in turn, regulates several biochemical events of the phototransduction cascade, a process generically referred to as Ca²⁺-feedback. The amplitude of the light-dependent Ca²⁺ concentration decrease and the Ca²⁺-feedback signal are, thus, proportional to photocurrent amplitude. Although the cytoplasmic Ca²⁺ level is proportional to current amplitude, it must be remembered that it is also dependent on rate of outward transport and cytoplasmic buffers and only modeling that fully accounts for all the physiological parameters can strictly anticipate the relationship between Ca²⁺ cytoplasmic changes and Ca²⁺ influx. Nonetheless, the biophysical features of the CNG channels in both rods and cones help assure that the transduction photocurrent is minimally affected by the photovoltage. This feature optimizes the photoreceptors' function: their phototransduction signal is regulated by light alone and little, if any, by membrane voltage. Significant functional corollaries of this fact are: (a) the time course of the photocurrent is different from that of the photovoltage, and (b) membrane voltage alone does not light- or dark-adapt photoreceptors.

As discussed in a recent forum (Andersen, 1999a), there does not exist a single, universal, and complete theory to describe ion permeation through channel proteins. The theoretical challenge is to develop a model that fully considers the structural details of the channel protein and explains the existence of high ionic flux rates in the face of high binding and selectivity. We analyzed our results using the theory first developed by Zwolinski et al. (1949) and based on Eyring's theory of absolute rate processes (Eyring et al., 1949). The theory describes the thermodynamics of the interactions between ions and binding sites within the channels and has been frequently and successfully used to describe ion permeation in other ion channels (see ). The theory is limited, however, because it is not required to define the molecular architecture of the binding sites. More specific physical models of ion diffusion and interaction such as those being developed, for example, through Molecular Dynamics (Allen et al., 1999, 2000) cannot yet be generally applied. Nonetheless, rate theory provides an understanding of the interactions between ions and CNG channels, particularly of the differences between rods and cones and the effects of voltage on Pf.

In our application, we inferred thermodynamic parameters for cone CNG channels from least-square optimized fits between theory and experimental data measured under simple ion solutions in detached membrane patches. To further reduce uncertainties in the values of adjustable parameters, we imposed constraints that demanded parameters have the same values when fitting data from different membrane patches and also data from rods and cones. We then used these parameters to simulate data expected under complex ion solutions in the intact cells and compared these data to those measured experimentally. Simulated and experimental data in the intact cells under physiological solutions matched reasonably well, except for the values of Pf, which differed by approximately a factor of two. We could have done additional computational manipulations to improve this match, for example, Wells and Tanaka (1997) have proposed that the transmission coefficient (κ in Eq. A1) for jumps that originate in the aqueous solutions may be adjustable. We believe the mismatch we report reflects the incompleteness of the theoretical model and prefer to pass up additional adjustments. In spite of its limitations, the thermodynamic model offers insights that rationally explain the complex I-V curves of the photoreceptor CNG channels under many ionic solutions as arising from the details of the interaction of the permeant ions with specific sites. It is not necessary to invoke additional physical mechanisms such as, for example, voltage effects on channel protein conformation.

The rate model developed here envisions the existence of two ion-binding sites within the permeation pore of the photoreceptor CNG channels. Data measured in both native membranes and recombinant CNG channels formed from α subunits alone are consistent with the existence of at least two divalent cation binding sites, each differentially accessible from the cytoplasmic or the extracellular membrane surfaces. The site accessible from the cytoplasmic surface binds Ca²⁺ so as to half-block inward current maximally at the reversal potential and at a concentration, ^CaK_1/2 around ∼1 mM in both rods and cones (Picones and Korenbrot, 1995). The extracellular site, in contrast, has a ^CaK_1/2 of ∼5 μM in rods and 60 μM in cones (Root and MacKinnon, 1993; Frings et al., 1995). This external site involves Glu-363 at the pore's external entrance since Ca²⁺-dependent block disappears when this amino acid is replaced by a neutral one (Root and MacKinnon, 1993; Eismann et al., 1994). This mutation, however, hardly affects the blocking properties of divalent cations added to the membrane cytoplasmic, confirming that the two sites are molecularly distinct. The molecular architecture of the external binding site involves Glu-363, but additional structural features are contributed by the nearby S5 and S6 domains, a reason binding features are not the same in rods in cones, although Glu-363 exists in the pore of both channels (Seifert et al., 1999). Although the features of channel structure that explain the voltage-dependence of Pf are to be defined in future work, it is noteworthy that the independence of Pf from membrane voltage is a feature of native photoreceptor channels, but apparently not of those formed from α-subunits alone (Dzeja et al., 1999).

APPENDIX

In the rate theory of ion permeation (Zwolinski et al., 1949) ion diffusion is treated as a sequence of point-to-point jumps into and across the channel pore, each jump governed by forward and reverse rate constants, k _i, whose value is given by:

(A1)

where κ is a frequency factor (s⁻¹) and −ΔGi** is the Gibbs free energy of activation between the points where jumps start and end. The frequency factor κ has historically been assigned the value of k_B*T/h, where k_B is Boltzmann's constant, T is absolute temperature, and h is Planck's constant (Eyring et al., 1949; Hille, 1975). Reexamination of the issue by Andersen (1999b) indicates that this value is valid only for elementary transitions that occur over distances less than the aqueous mean free path (∼0.1 A). A more reasonable value assignment for κ would be 10⁹ − 10¹⁰ s⁻¹, the frequency of diffusional transitions over nm distance. To apply this theory, an energy profile is hypothesized to exist along the ion diffusion path within the channel. The heights of energy barriers and depths of energy wells in this profile are defined, as well as their location along the electrical membrane thickness (see Fig. 5). From the energy profile, kinetic rates are computed (Eq. A1), and from the rates the probability of occupancy of every possible binding site. The adequacy of the theory is tested by its ability to generate I-V curves that match experimental data.

Abridged forms of the rate theory have been used before to analyze cGMP-gated currents measured under simple salt solutions (Picones and Korenbrot, 1992; Zimmerman and Baylor, 1992; Haynes, 1995). Wells and Tanaka (1997) developed a more complete form of the theory to analyze cGMP-gated current in intact rods under physiological solutions. Ours is an extension and refinement of their model. Mathematical details on model development can be found in Hille (1975), Begenisich and Cahalan (1980), and Alvarez et al. (1992).

The theoretical model we develop here assumes free energy is zero in the intra and extracellular space (Hille, 1975; Alvarez et al., 1992). The model consists of three barriers and two wells, that is, it proposes there exist two ion binding sites along the ion permeation path, each separated from the other (and the membrane surfaces) by an energy barrier (Fig. 5). This is the simplest model that adequately matched our experimental results, single site models were insufficient. In a rate theory model, the n number of allowed p occupancy states, for w binding sites and m ionic species is n = (m + 1)^w. For two sites and four ions, Na⁺, K⁺, Ca²⁺, and Mg²⁺, for example, n = 25. If each binding site can be occupied by only one ion at a time and if ions are allowed to move only into unoccupied sites, then it can be shown that only 24 reversible transitions are allowed between the 25 occupancy states. Each of the 24 transitions has forward and reverse rate constants, hence, a total of 88 rate constants mathematically define the model. The value of each of the 88 rate constants can be computed from Eq. A1. The issue then becomes how to compute the value of ΔGi** for each transition.

ΔGi** is computed by considering that ion jumps between sites are driven by the sum of chemical and electrostatic energies. The chemical energy is computed as the difference between the energy of the barrier over which the transition occurs minus the energy of the well from which the transition starts (in RT units). The electrostatic energy depends on the membrane voltage, Vm, and the location of the binding site within the membrane. This component is computed as (di − dj)(VmzF/RT), where (di − dj) is the distance between the jumping sites in fractional units where membrane thickness ranges between 0 (extracellular) and 1 U (cytoplasmic). F is Faraday's constant and z is the permeant ion's valence. In addition, electrostatic energy also reflects the interaction between a jumping ion and ion(s) that may already bound to channel sites. This interaction is sometimes neglected (pore with independence: Hille, 1975; Begenisich and Cahalan, 1980), but most often it is included as an empirical coefficient that multiplies the computed rates and is adjusted to improve fit between data and theory (as introduced by Hille and Schwarz, 1978; e.g., Bahring et al., 1997). Following Alvarez et al. (1992), we include ion–ion electrostatic interactions by adding a term to ΔGi** when computing rates of transitions that occur when one site is already occupied. The wells and barriers around an occupied site are shifted by the product of the charges of the moving and bound ions divided by the distance between the bound ion and those wells and barriers times an adjustable proportionality constant, Ainter, given in RT units. For example, when a transition occurs in the absence of other ions, e.g., Na⁺ from well G3 to the cytoplasmic, the forward rate is:

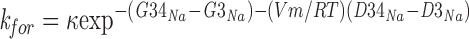The same rate constant computed when Ca²⁺ is bound to well G2 is:

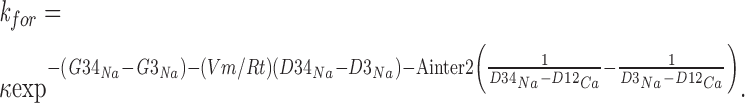Jumps that start from a site within the channel, G2 or G3, are first order reactions, whereas those of jumps that start in the bathing solutions are second order and, therefore, rate constants are defined to include the ion concentration in the membrane-bathing solutions (Hille, 1975). We expressed concentration in mole fraction (Alvarez et al., 1992) calculated from ion activities evaluated using known activity coefficients (monovalent: Robinson and Stokes, 1959; divalent: Butler, 1968) and performed all calculations at 293°K. For example, the forward rate constant at which Na⁺ jumps from the extracellular solution into well G2 when Ca²⁺ is already bound to well G3 is,

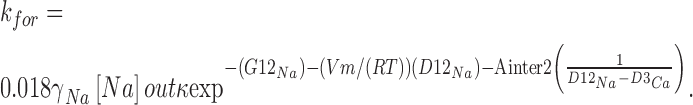
where [Na ⁺ ]out is extracellular Na⁺ concentration in Molar, γ_Na is activity coefficient, and 0.018 yields concentration in mole fraction. We neglected surface potential and assumed ion concentrations at the channel's ends are the same as in bulk. The value of each rate constant is the maximum possible rate of transition over each energy barrier (in units of transitions per second).

Having specified the values of the 88 rate constants, the rates of formation of each of the 25 occupancy states, dp ⁱ/dt, are defined through the rules of chemical kinetics (Hille, 1975). This yields a system of simultaneous differential equations that describe the probability of every one of the occupancy states. Under steady-state conditions, when dp ⁱ/dt = 0, the system of differential equations can be written in a matrix form (Begenisich and Cahalan, 1980). Solving the matrix yields the values of the probability of existence of every one of the 25 occupancy states. Each probability value is constant and their sum is one. We computed probability values by solving the appropriate matrices either by the method of Colquhoun and Hawkes (1987) or with the lsolve algorithm in MathCad (MathSoft, Inc.) with indistinguishable results.

Unidirectional ion flux is the product of the probability the ion jumps over a designated site in the channel times the jump's rate. We computed the net flux of every ion from the algebraic sum of the influx and efflux rates at which they cross the central barrier (G23 in Fig. 5). In general, this was computed as:

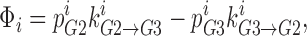where Φ is flux, 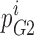is the probability that well 2 is occupied by ion i, 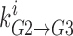is the rate at which the ion jumps from well 2 into well 3, is the probability that well 3 is occupied, and 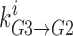is the rate at which the ion can jump from well 3 into well 2. Currents (in pA) are computed by multiplying flux by the elementary electronic charge and the ions' valence.