Addressing Ceiling Effects in Health Status Measures: A Comparison of Techniques Applied to Measures for People with HIV Disease

Abstract

Objectives

To compare different approaches to address ceiling effects when predicting EQ-5D index scores from the 10 subscales of the MOS-HIV Health Survey.

Study Design

Data were collected from an HIV treatment trial. Statistical methods included ordinary least squares (OLS) regression, the censored least absolute deviations (CLAD) approach, a standard two-part model (TPM), a TPM with a log-transformed EQ-5D index, and a latent class model (LCM). Predictive accuracy was evaluated using percentage of absolute error (R¹) and squared error (R²) predicted by statistical methods.

Findings

A TPM with a log-transformed EQ-5D index performed best on R¹; a LCM performed best on R². In contrast, the CLAD was worst. Performance of the OLS and a standard TPM were intermediate. Values for R¹ ranged from 0.33 (CLAD) to 0.42 (TPM-L); R² ranged from 0.37 (CLAD) to 0.53 (LCM).

Conclusions

The LCM and TPM with a log-transformed dependent variable are superior to other approaches in handling data with ceiling effects.

Health-related quality of life (HRQoL) is increasingly used to measure health status. Health profile and preference-based approaches are two types of methods frequently used to measure HRQoL. Health profiles tap multiple dimensions of health. Preference-based approaches quantify the extent to which an individual prefers specific health states using a single index from 0 (death) to 1 (full health). The MOS-HIV Health Survey (Wu et al. 1997) and EQ-5D (The EuroQol Group 1990) are typical health profile and preference-based instruments, respectively.

The availability of preference-based HRQoL data is limited because direct assessment is not always feasible. Therefore, researchers have attempted to predict preference-based scores from health profiles, generally using ordinary least squares (OLS) regression (Fryback et al. 1997; Franks et al. 2004).

A common phenomenon observed in both health profile and preference-based measures is that the score distribution tends to be skewed to the left. This is called the “ceiling effect.” When data have pronounced ceiling effects, the use of OLS regression violates the statistical requirement for linearity of conditional expectation, leading to inaccurate predictions of preference-based scores and inaccurate identification of predictor variables (Kennedy 1998). Several methods have been proposed to address ceiling effects, such as Tobit models, the censored least absolute deviation (CLAD) approach, two-part models (TPM), and latent class models (LCM) (Greene 2003).

The Tobit and CLAD models are preferable to OLS in the presence of a ceiling effect or censored dependent variable. The Tobit model assumes that there is a true unobservable dependent variable that depends linearly on independent variables. The observable dependent variable is defined to be equal to the unobserved variable whenever the true unobserved variable is greater than or equal to the ceiling value. The Tobit model assumes that the error terms are normally distributed with uniform variance (Greene 2003). Unfortunately, evidence suggests that the distribution of utility scores does not follow those assumptions (Austin 2002a). The CLAD approach is based on an assumption that the median will be more robust to ceiling effects than the mean. The coefficients are estimated so as to minimize the sum of the absolute deviations from the regression line (Arabmazar and Schmidt 1981; Johnston 1997).

A TPM approach is a more flexible way to address the fact that the HRQoL scores usually have mixed distributions that contain a disproportionate mass of observation at the ceiling and a left-skewed distribution of observations not at the ceiling. The “two parts” model (1) the probability that the dependent variable (e.g., EQ-5D index) can attain the full score and (2) the distribution if the full score is not attained. Both parts are combined in a joint model to predict the dependent variable using the subject's predictors.

The LCM is another approach to address data with ceiling effects. This approach is considered by some to be more flexible than the TPM because LCM can handle situations where there are two (or more) classes, with one class being very healthy (i.e., higher utility index) and another group being less healthy (i.e., lower index), as opposed to a TPM which models perfectly healthy (index=1) versus other than perfectly healthy (index <1) (Deb and Trivedi 1997, 2002).

Although several studies analyzing HRQoL have used the Tobit model to address ceiling effects (Austin, Escobar, and Kopec 2000; Austin 2002b; Clarke, Gray, and Holman 2002; Sullivan, Lawrence, and Ghushchyan 2005), only three have applied the CLAD (Austin 2002b; Clarke, Gray, and Holman 2002; Sullivan, Lawrence, and Ghushchyan 2005) and none have used a TPM or LCM.

The purpose of this study was to compare these statistical methods to predict preference-based HRQoL scores from health profiles for persons with HIV, taking into account ceiling effects. We compared performance (predictive accuracy and error) of these methods to a standard regression model. As an example, we estimated the EQ-5D index from the MOS-HIV. We used a cross-validation method to evaluate the performance of each statistic method.

METHODS

Data Collections

The parent study was a randomized, double-blind clinical trial of delavirdine mesylate, which is in a nonnucleoside reverse transcriptase inhibitor (NNRTI) of HIV (Weinfurt et al. 2000). This drug is used to treat a range of HIV-infected patients, including newly infected asymptomatic patients and those who have AIDS. In the current analysis, patients were included if they completed both the EQ-5D and MOS-HIV at baseline.

The Instruments

The EQ-5D instrument comprises five items (mobility, self-care, usual activities, pain/discomfort, and anxiety/depression) and one visual analogue scale (The EuroQol Group 1990). Different combinations of responses are integrated into a single preference-based HRQOL score (EQ-5D index) using preference values from a U.S. general population (Shaw, Johnson, and Coons 2005). EQ-5D index is anchored by score=1 for perfect health and score=0 for lowest possible health (death). The EQ-5D index also allows a small negative value (worse than death) (Dolan 1997).

The MOS-HIV Health Survey is a 35-item instrument measuring 10 health domains: physical function (PF), pain (PN), role function (RF), social function (SF), general health perceptions (GH), vitality (VT), cognitive function (CF), quality of life (QL), health distress (HD), and mental health (MH). Domain scores range from 0 to 100, with higher scores indicating better health (Wu et al. 1997).

Analytic Scheme and Statistical Approaches

We applied an analytic scheme with 10 subscales of the MOS-HIV to examine the contribution of different predictor variables to EQ-5D index. We examined five statistical approaches: OLS regression, the CLAD approach, a standard two-part model (TPM), a TPM with a log-transformed EQ-5D index (TPM-L), and an LCM.1

OLS attempts to estimate EQ-5D index scores through minimizing the sum of the squared differences between observed and fitted values from a linear predictor assumed to be the mean of the observed data. By contrast, CLAD assumes the median is more robust than the mean to ceiling effects and tries to minimize the sum of absolute differences between observed and fitted values. TPM splits the data into two parts—for those that are at ceiling and those are below the ceiling. TPM-L log-transforms the data for those that are below the ceiling to explicitly recognize the skewed distribution of the data. In contrast to TPM, LCM attempts to classify the data using latent discrete states of health status, within each of which the outcome is assumed to be more homogeneously distributed. It is helpful to point out more specifically the characteristics of each approach:

The OLS approach assumes the conditional expectation of the EQ-5D index y is linear in the vector of predictor variables x, namely,

(1)

The coefficients are estimated by minimizing the sum of the squared deviations between observed and fitted values. The EQ-5D index is then predicted by its estimated expectation (1) using the estimated coefficients. By construction, this provides the best linear prediction of EQ-5D index with respect to squared error loss (Johnston 1997).

The second approach, CLAD, is one form of least absolute deviations (LAD) regressions that are commonly used by economists to model data with skewed distributions (Johnston 1997). Contrary to the OLS, CLAD models the median EQ-5D index score. The coefficients β_CLAD were chosen in order to minimize the sum of absolute deviations from the regression line, |y_i−x_iβ|. The EQ-5D index is then predicted by xβ_CLAD.

The third approach, a standard TPM, uses two models. The first part models the probability that an individual has EQ-5D index at the ceiling, with the logistic regression equation

(2a)

The second part models the EQ-5D index for those individuals whose EQ-5D scores are below the ceiling using a regression model of approach 1, with

(2b)

The EQ-5D index is then predicted by the estimated overall expected score, which based on (2a) and (2b) is

(2c)

The fourth approach, TPM-L, is also a TPM, but recognizes explicitly that in the second-part model of the EQ-5D index below the ceiling, the predictions should be bounded by that ceiling. Recognizing this explicitly also addresses the skewness of that part of the model. To do this, model (2b) is replaced by the model for which

(3a)

Under this model, the characteristic function of the normal distribution can be used to show that the overall expected score is given by

(3b)

After estimation of the parameters by maximum likelihood, the EQ-5D index is then predicted by model (3b). Note that the prediction based on this model involves the variance of the distribution of the second part.

For the final approach, LCM, we hypothesized that the underlying unobserved heterogeneity which splits the population into latent classes is based on an individual's latent health status. In this study, we used five items of the EQ-5D questionnaire as an indicator for the latent class.

Predictive Accuracy with Cross-Validation

We used an empirical cross-validation method to estimate the predictive accuracy of each model, for the population averages of absolute error and squared error. We randomly divided the data into 90 percent for model fitting and 10 percent for validation. We calculated the R¹ and R² coefficients to demonstrate the percentage of absolute error and squared error that were predicted by the statistic methods, respectively. We calculated the estimates of R¹ and R² as follows:

(4)

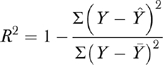(5)

where, Y denotes the observed EQ-5D index score, 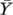is the mean of observed EQ-5D index score, 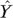denotes predicted EQ-5D index score, and any prediction over 1 would have been truncated to 1.

The above process was repeated in 1,000 bootstrap samples, and R¹ and R² for the population were estimated by the corresponding averages across bootstrap samples. The 95 percent central intervals (CIs) for the two population accuracy parameters were calculated using the standard deviation of the bootstrap estimates. In this study, the LCM was performed using Mplus (Muthen and Muthen 2004). The rest of the analyses was performed using STATA 9.0 (STATCorp 2005).

RESULTS

There were 1,126 patients included in this study. The distributions of age, gender, race, CD4+ cell count, and HIV RNA were similar for the excluded patients versus those in the analyses (all p>.05). Of these, mean age was 37.4 years (SD: 8.4); 87 percent were male; 68, 20, 12 percent were white, black, and other racial groups, respectively. Mean CD4+ cell count was 141.8 cells/mm³ (SD: 91.1) and median HIV RNA was 5.8 log copies/mL (SD: 0.6).

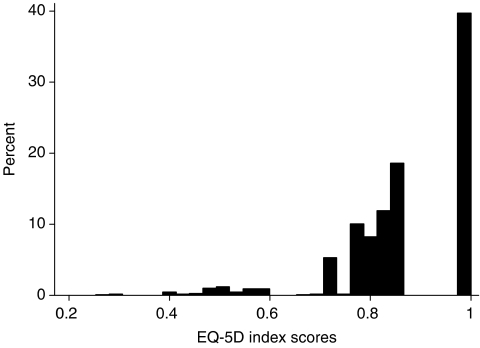
Table 1 presents the score distribution of the EQ-5D index and MOS-HIV subscales. The score distribution of the EQ-5D index was significantly skewed to the left (Figure 1), with 40 percent of the subjects obtained the highest score. Some of the MOS-HIV subscales were also skewed to the left (>30 percent with the highest score).

Table 1.

Distribution and Correlations among EQ-5D Index and MOS-HIV Subscale Scores

	Mean (SD)	25 Percentile	50 Percentile	75 Percentile	Ceiling Effects (%)	Correlation Coefficients with the EQ-5D Index
EQ-5D index scores	0.87 (0.13)	0.80	0.84	1	40
MOS-HIV
Physical function	79.4 (23.3)	66.7	91.7	100	35	0.52
Pain	78.2 (21.8)	66.7	88.9	100	33	0.64
Role function	69.2 (42.3)	50	100	100	62	0.52
Social function	83.7 (23.1)	80	100	100	57	0.53
General health perceptions	51.4 (26.0)	30	50	75	3	0.54
Vitality	61.2 (22.2)	45	65	80	2	0.58
Cognitive function	83.9 (20.4)	75	90	100	36	0.49
Quality of life	69.1 (20.9)	50	75	75	19	0.49
Health distress	72.0 (25.1)	60	80	90	15	0.54
Mental health	71.1 (19.5)	56	76	88	3	0.57

Figure 1.

Distribution of EQ-5D Index Scores.

Table 2 indicates which variables were relatively important for each model. The R² gain of a specific subscale is defined as 1−(R² of a scheme that excludes that subscale divided by R² of a scheme that includes all subscales). The subscales significantly predicting EQ-5D index scores were the PF, PN, RF, and MH (most with p<.05; R² gain: 0.01–0.06, 0.07–0.14, 0–0.1, and 0.02–0.03, respectively). In the CLAD approach, the R² gain for some subscales was negative, implying that the additional noise in estimating those subscales (in data for model fitting) was larger than the additional theoretical gain of predictive power (in data for model validation).

Table 2.

Coefficients of the MOS-HIV Subscales for Predicting EQ-5D Index Scores

	OLS		CLAD		TPM			TPM-L			LCM
Subscales†	β‡	R2 Gain, (%)§	β	R2 Gain (%)	Part 1 Odd Ratio	Part 2 β	R2 Gain (%)	Part 1 Odd Ratio	Part 2 β	R2 Gain (%)	Part 1 Odd Ratio	Part 2 β	R2 Gain (%)
PF	0.7***	1.4	0.8**	6.0	1.0	1.0***	2.3	1.0	−3.3***	2.1	1.0	1.1***	1.5
PN	1.9***	8.0	2.1*	13.8	1.1***	1.0***	7.7	1.1***	−4.2***	6.6	1.1***	1.0***	8.1
RF	0.4***	0.0	0.4	9.8	1.0**	0.1	0.5	1.0**	−0.7	3.2	1.0***	0.1	0.5
SF	0.3	−0.4	−0.2	−2.4	1.0	0.2	−0.4	1.0	−0.6	0.4	1.0	0.2	0.0
GH	0.2	0.0	1.4	−2.0	1.0	−0.2	−0.1	1.0	0.8	0.2	1.0	−0.1	0.0
VT	0.1	0.0	0.7	−0.7	1.0	−0.1	0.0	1.0	−0.8	0.0	1.0	−0.1	0.0
CF	0.1	0.0	0.1	0.6	1.0	0.1	0.0	1.0	−0.3	0.0	1.0	0.2	0.0
QL	0.2	0.1	0.3	−0.3	1.0	0.1	0.2	1.0	−0.3	0.1	1.0	0.1	0.1
HD	0.4*	0.4	0.5	3.0	1.0	0.4	0.5	1.0	−1.3*	0.5	1.0*	0.3	0.8
MH	1.4***	3.1	1.4**	3.1	1.0***	1.1***	3.0	1.0***	−3.6***	2.4	1.0***	1.1***	2.7

^†Inclusions of demographic and clinical variables did not improve predictive accuracy.

^‡β (× 1,000).

^§R² gain: 1−(R² of a scheme excluding a specified subscale/R² of a scheme including all subscales).

^*p<.05

^**p<.01

^***p<.001.

OLS, ordinary least regression; CLAD, censored least absolute deviation; TPM, two-part model; TPM-L, two-part model with log-transformed EQ-5D index; LCM, latent class model; PF, physical function; PN, pain; RF, role function; SF, social function; GH, general health perceptions; VT, vitality; CF, cognitive function; QL, quality of life; HD, health distress; MH, mental health.

The predictive accuracy of each statistical approach is summarized in Table 3. When comparing the point estimates of predictive accuracy, the findings suggested the TPM-L and LCM performed best on R¹ and R², respectively. In contrast, the CLAD was worst. The performances of the OLS and a standard TPM were intermediate. The ranges of the R¹ were: 0.33 (CLAD) to 0.42 (TPM-L) and the R² were: 0.37 (CLAD) to 0.53 (LCM). Although the point estimates for predictive accuracy demonstrated that the TMP-L and LCM outperformed the other approaches, the 95 percent CIs of point estimates were overlapping across all approaches, suggesting none of the methods was superior to others. The method with no cross-validation generally yielded inflated accuracy in R¹ and R². The TPM-L and CLAD approaches, respectively, demonstrated the best and worst predictive accuracy in both R¹ and R².

Table 3.

Predictive Accuracy of Statistical Models

	No Cross-Validation		Bootstrap (BS) Cross-Validation
				BS 95% CI of R1			BS 95% CR of R2
	R1	R2	R1	Low	High	R2	Low	High
OLS	0.35	0.54	0.35	0.20	0.51	0.43	0.12	0.74
CLAD	0.35	0.50	0.33	0.16	0.51	0.37	0.003	0.73
TPM	0.35	0.53	0.35	0.19	0.51	0.41	0.09	0.74
TPM-L	0.42	0.58	0.42	0.27	0.57	0.48	0.20	0.77
LCM	0.40	0.56	0.38	0.29	0.48	0.53	0.41	0.64

R¹, % of the absolute error predicted by the model; R², % of the square error predicted by the model; 95% CI, 95% central intervals; OLS, ordinary least squares; CLAD, censored least absolute deviation; TPM, two-part model; TPM-L, two-part model with log-transformed EQ-5D index; LCM, latent class model.

DISCUSSION

Attempts to estimate patient utilities from descriptive HRQoL data are compromised by ceiling effects. We addressed this problem using the example of applying the MOS-HIV to estimate the EQ-5D index. Our results suggested LCM performed best in terms of R²=53 percent. However, the TPM with a log-transformed dependent variable performed best in R¹=42 percent. Both models demonstrated superiority to the OLS approach.

The TPM addresses ceiling effects by modeling the outcomes separately for subjects with ceiling scores and for those without ceiling scores. In the untransformed TPM, ceiling effects can be a problem as the model for the latter part is still unbounded by the ceiling, but this is addressed by an appropriate transformation as with the TPM-L model.

The Tobit estimators are theoretically more consistent and efficient than the TPM unless the assumptions of normality and homoskedasticity are violated to an important degree (Kennedy 1998; Greene 2003), for example, as defined by the Kullback–Leibler distance (Kullback and Leibler 1951). The TPM model is a generalization of the Tobit model in the sense that if the Tobit model is correct, then a Gaussian-based TPM model is also correct although less efficient. However, if the assumptions of Tobit model are too stringent, the TPM estimation may be inconsistent. In addition, TPM may suffer from the problem of multicollinearity between explanatory variables and the probability correction variables (inverse Mills ratio) (Kennedy 1998). We examined the residuals of Tobit model against the predictor variables and found that the residuals were not constant across the level of each predictor. Therefore, our data empirically suggest that the Tobit model at least violates the assumption of homoskedasticity. A simulation study has suggested that the violation of homoskedasticity for the Tobit model can lead to significantly biased estimators than the violation of normality assumption (Austin, Escobar, and Kopec 2000).

The TPM and LCM both require investigators to specify the probability distribution of the data. Although this may lead to misspecification of the TPM and LCM, econometric evidence suggests that the impact is smaller for LCM than the TPM. That is because the LCM is more flexible and can serve as a better approximation to any true, but unknown, probability density than the TPM (Deb and Trivedi 1997).

Our results have implications for research on HIV treatments and other research on HRQoL. For HIV clinical trials, when EQ-5D survey is not available, then the statistical approaches (TPM-L or LCM) developed in this study, together with 10 subscales of the MOS-HIV (Table 2) can provide a useful way to derive EQ-5D index scores. Likewise, our methods can be applied to investigate preference-based HRQoL using other health profiles and different populations. For the general population, the ceiling values are more prevalent than for the HIV patients enrolled in this study. In contrast to the 40 percent of patients obtaining the maximum EQ-5D index score in this study, 45 percent (Franks et al. 2004) and 50 percent (Luo et al. 2005) of the EQ-5D index scores were at the ceiling in two recent surveys using U.S. general samples.

Our study has several limitations. First, the generalizability of our mapping algorithm may be limited because we enrolled patients in a clinical trial rather than from a general population of people with HIV. Clinical trials generally apply inclusion/exclusion criteria to enroll healthier patients. Second, the theoretical boundary of EQ-5D index is between 0 and 1. However, the EQ-5D index allows a small negative value (worse than death), which would lead to the generation of missing values if log transformation is used. Although negative EQ-5D index scores were not observed in our study and are relatively uncommon in other studies, they can be addressed with our TPM-L approach by first applying a transformation to place the values to the (0, 1) scale.

CONCLUSIONS

The estimation of preference-based HRQoL scores using health profiles can facilitate the economic valuations of treatments, especially when preference-based scores are not available directly. However, preference-based HRQoL measures are subject to ceiling effects, which may compromise predictive accuracy. Our results demonstrated that in using the MOS-HIV subscales as predictors, the application of the LCM and TPM-L best captured the EQ-5D index, with up to 53 percent in the R² and 42 percent in R¹, respectively. The empirical findings of this study did not fully support the propositions of theoretical models (e.g., CLAD and Tobit models) to address the ceiling effects.