Abstract
Transposable elements (TEs) often accumulate in regions of the genome with suppressed recombination. But it is unclear whether this pattern reflects a reduction in the efficacy of selection against deleterious insertions or a relaxation of ectopic recombination. Discriminating between these two hypotheses has been difficult, because no formal model has investigated the effects of recombination under the deleterious insertion model. Here we take a simulation-based approach to analyze this scenario and determine the conditions under which element accumulation is expected in low recombination regions. We show that TEs become fixed as a result of Hill–Robertson effects in the form of Muller's ratchet, but only in regions of extremely low recombination when excision is effectively absent and synergism between elements is weak. These results have important implications for differentiating between the leading models of how selection acts on TEs and should help to interpret emerging population genetic and genomic data.
UNDERSTANDING how the proliferation of transposable elements (TEs) is kept in check remains an important theoretical and empirical problem in evolutionary genetics. TEs are widely considered to be intragenomic parasites, with considerable evidence that they are generally harmful (Charlesworth et al. 1994; Lynch 2007, Chap. 7). But despite their adverse effects, TEs represent a significant proportion of the nuclear DNA of many organisms and contribute greatly to genome evolution (Kidwell 2002). The selfish DNA theory posits that the abundance of TEs is regulated by a balance between the tendency for elements to increase in number by transposition and natural selection against the deleterious effects they impose upon their hosts (Doolittle and Sapienza 1980; Orgel and Crick 1980). However, the nature of the selective forces that limit TE abundance is still poorly understood.
The deleterious effects of TEs have been attributed to three main sources: mutations resulting from insertions into genes or regulatory sequences (“deleterious insertion model”; Finnegan 1992); chromosomal rearrangements caused by ectopic recombination between elements in nonhomologous insertion sites (“ectopic exchange model”; Montgomery et al. 1987); and direct costs due to transposition activity itself (“deleterious transposition model”; Brookfield 1991). An expected consequence of selection acting to limit element proliferation is that TEs should be more abundant in regions of the genome where they are less likely to be deleterious and/or where natural selection is less effective at removing them. However, part of the problem in discriminating between the different models is that all three make similar and nonmutually exclusive qualitative predictions regarding the genomic distribution of elements. Despite extensive theoretical and experimental results, no general consensus exists on the relative importance of these different factors (Biémont et al. 1997; Charlesworth et al. 1997; Nuzhdin 1999).
Many studies have tried to test the models by comparing the distribution and abundance of TEs in low vs. high recombination regions of the Drosophila genome. In the genomes of Drosophila melanogaster and D. buzzatii, high TE densities have been found in areas of reduced recombination (Bartolomé et al. 2002; Rizzon et al. 2002; Bergman et al. 2006; Casals et al. 2006; Fontanillas et al. 2007). These genomic data are consistent with in situ hybridization data in Drosophila that show TEs accumulating in regions where recombination is suppressed, such as the proximal and distal arms of the major autosomes (Langley et al. 1988; Charlesworth et al. 1992; Maside et al. 2001; but see Hoogland and Biémont 1996), in polymorphic chromosomal inversions (Eanes et al. 1992; Sniegowski and Charlesworth 1994), and on the neo-Y chromosome of D. miranda (Steinemann and Steinemann 1998; Bachtrog 2003). Since areas of low meiotic recombination are expected to have low rates of ectopic recombination (Langley et al. 1988; Montgomery et al. 1991; Goldman and Lichten 1996, 2000), these results may be taken as evidence for the ectopic exchange model.
However, these results are also consistent with the deleterious insertion model, since low recombination regions have lower gene densities (Adams et al. 2000; Fullerton et al. 2001) and experience weaker effective selection against deleterious insertions (Charlesworth and Langley 1991). Similarly, TE accumulation in low recombination regions is expected under the deleterious transposition model, which makes comparable predictions regarding element patterning to the deleterious insertion model (Brookfield 1991). Therefore, all three models predict a greater abundance of elements in genomic regions of reduced recombination, and no firm conclusions can be drawn from this observation alone as to whether the accumulation of TEs in low recombination regions reflects differences in the rate of ectopic exchange or a reduction in the efficacy of selection acting against deleterious element insertions.
While a strong theoretical framework exists for predicting the effects of recombination rate on ectopic exchange and its implications for TE distribution and abundance (Langley et al. 1988; Charlesworth et al. 1992), no theoretical studies have taken into account the effects of close linkage on the efficacy of selection under the deleterious insertion model. Local recombination should be an important factor affecting element patterning because a deleterious TE at one site can reduce the efficacy of selection acting at neighboring linked insertion sites, a phenomenon known as the Hill–Robertson effect (Hill and Robertson 1966; Felsenstein 1974). This reduces the effective population size, enhances the importance of genetic drift, and can lead to the fixation of TEs in nonrecombining regions through the process of Muller's ratchet (Muller 1964; Felsenstein 1974). These effects should be influenced by a number of factors, including local recombination rates, effective population sizes, the strength of selection, and the rate of occurrence of new insertions. These factors have been studied for classical mutational models (e.g., Gordo and Charlesworth 2000, 2001; McVean and Charlesworth 2000; Comeron and Kreitman 2002; Keightley and Otto 2006), but the unique ability of transposable elements to replicate autonomously through transposition, and excise from the genome, could lead to distinct patterns and evolutionary dynamics. A better understanding of the genomic distribution expected from these effects should help differentiate the deleterious insertion model from the ectopic exchange model.
Theoretical considerations of TEs under the deleterious insertion model have almost universally assumed a constant recombination rate across the entire genome. Part of the reason that the effects of variable recombination have not been well-studied is that understanding these processes often requires a simulation-based approach. This is in contrast to the relatively simple prediction of the ectopic exchange model that the number of TE copies inserted in a given region is expected to be inversely related to the recombination rate (Langley et al. 1988; Charlesworth et al. 1992). In this article, we develop a simulation model that simultaneously considers a genome with both high and low recombination regions. We then identify conditions and parameters under which element accumulation in regions of reduced recombination is expected. We show that the deleterious insertion model can explain an increased abundance of TEs in low recombination areas only when individual element insertions become fixed at the population level. We discuss the results of our simulations in relation to the genomic data and population surveys of D. melanogaster to try and distinguish between the leading hypotheses for why TEs build up in low recombination regions.
METHODS
Computer simulations were used to examine the effects of reduced recombination on the distribution and abundance of transposable elements in the genome. The model was implemented by modifying the simulation program of Dolgin and Charlesworth (2006) to incorporate sexual reproduction and recombination. C++ files are available upon request. Random numbers were generated using the Mersenne Twister pseudorandom number generator (Matsumoto and Nishimura 1998), adapted for C++ by J. Bedaux (http://www.bedaux.net/mtrand/).
Population and genome:
We consider a diploid population of a constant size, N, with discrete nonoverlapping generations. The genome is composed of four chromosomes: three large recombining chromosomes, each representing 30% of the genome, and one smaller chromosome, representing 10% of the genome. This is intended to provide a rough portrayal of the D. melanogaster genome, for which most data on TE distributions are available, although we have exaggerated the size of the small, noncrossing over fourth chromosome (Ashburner et al. 2004). The larger chromosomes are able to carry as many as 1000 elements each, permitting a large number of potential insertions, with a recombination frequency, r, of 10−3 between any two adjacent potential insertion sites, resulting in one crossover event per chromosome per generation on average. The smaller chromosome can carry a maximum of 333 elements, and the recombination frequency is adjusted in different simulations to analyze the effects of a genomic region with reduced and null recombination, respectively.
Simulations:
The simulation is initiated by randomly inserting N elements into the population (i.e., 1 copy per genome on average). Each generation then starts with reproduction, involving selection and recombination, followed by transposition and excision. In each generation, individuals are sampled as follows to produce a new offspring population of size N. For each offspring, two parents are randomly selected. Each parent then creates a gamete, with the number of crossovers per chromosome drawn from a Poisson distribution according to the length and recombination rate of the chromosome and a uniform distribution of crossover positions. The gametes are then combined, and the resulting offspring are subject to selection, with the probability of survival proportional to their fitness values, as described by Dolgin and Charlesworth (2006). Fitness is assumed to be a decreasing function of TE abundance. This is essential to allow for a stable equilibrium copy number under free recombination; otherwise, TEs will proliferate in an unbounded fashion regardless of recombination rate (Charlesworth and Charlesworth 1983). We model the fitness of an individual with n elements by an exponential quadratic, decreasing function of the TE copy number,
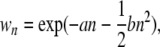 |
(1) |
where a and b are constant selection coefficients (Charlesworth 1990), and dominance is assumed to be intermediate at each insertion site (i.e., n is the sum of all the elements in the diploid genome). The model permits TEs to segregate in the population and implicitly assumes that insertions causing large fitness effects are rapidly eliminated by selection and can be ignored (Charlesworth and Langley 1991). After formation of the new offspring population, transposition and excision are assumed to occur randomly throughout each genome under a Poisson process, with the TE copy number increasing with probability u per element and decreasing with probability v per element.
Model parameters:
Simulations were generally run for 106 generations, although in cases where nonequilibrium TE accumulation was especially rapid, simulations were run for fewer generations. At every 1000th generation, we surveyed the TE copy number on each chromosome and the number of sites where a TE was fixed across the entire population. At least 10 simulations were performed for each combination of parameters investigated. We set the parameters in our model to match estimates from Drosophila populations, where average transposition rates for all classes of elements are ∼10−4 per element per generation, with excision rates at least one order of magnitude smaller (Nuzhdin and Mackay 1995; Suh et al. 1995; Vieira and Biémont 1997; Pasyukova et al. 1998; Maside et al. 2000). Since equilibrium requires equality of rates of origination and removal of elements, the strength of selection against segregating elements should be of the order 10−5–10−4 per copy (Charlesworth et al. 1994). Because of synergism between elements, the strength of selection depends on both a and b, so we set a = 10−5 and let b vary from 10−6 to 10−5.
However, to achieve more simulations in a given amount of computation time, we adjusted the parameters following the scaling employed and validated in the simulations of Dolgin and Charlesworth (2006), which has also been used elsewhere (Le Rouzic et al. 2007; Söderberg and Berg 2007). This scaling involves increasing the transposition–excision and selection parameters (u, v, a, and b) by two orders of magnitude, while decreasing N and the number of generations by the same factor. Because we are maintaining the products of the deterministic forces and the effective population size constant, this should lead to the same evolutionary outcome, provided that all evolutionary forces are weak (Ewens 2004, Chap. 4). In the results below, we present the uncorrected parameter values as used in the simulations, although to reflect biologically relevant values, all the parameters would need to be scaled 100-fold.
RESULTS
With the quadratic fitness formula (Charlesworth 1990; Dolgin and Charlesworth 2006), the expected equilibrium mean TE copy number under free recombination with low frequencies of elements at each occupied site is given by
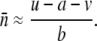 |
(2) |
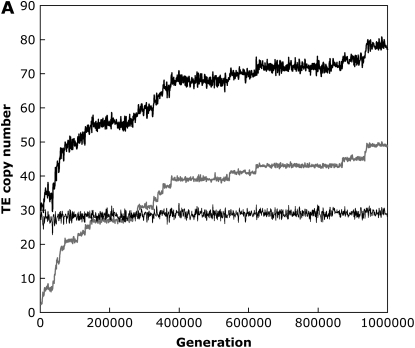
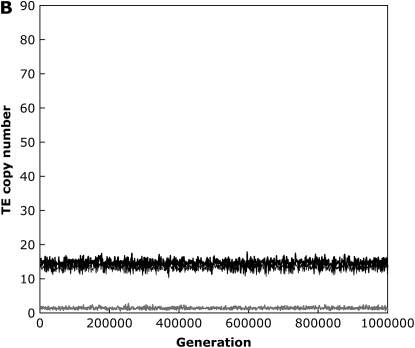
With the standard rate of crossing over across our entire simulated genome, including the small (“fourth”) chromosome, we found that the TE copy number in simulations of large populations (N = 103) equilibrated rapidly and matched this predicted amount within ±1 element for all parameter combinations tested (results not shown). In the absence of excision, when we set the recombination rate on the fourth chromosome equal to zero, equilibrium copy numbers as predicted by Equation 2 were still established when the synergism coefficient, b, was large, implying strong synergistic interactions between insertions. Under these conditions, ∼10% of the total number of elements in the genome were on the nonrecombining fourth chromosome, which is directly proportional to the size of the chromosome in our simulations. However, with lower values of b, the genome accumulated more elements than the equilibrium expectations (Figure 1). This is the result of a buildup of elements on the nonrecombining fourth chromosome, as TEs become fixed due to Muller's ratchet (Muller 1964; Felsenstein 1974). The shift between TEs either equilibrating or accumulating on the nonrecombining chromosome occurs quite suddenly following slight changes in the synergism coefficient, b. By analyzing a single simulation run, we can observe this shift and see these fixations as discrete jumps in the TE copy number on the fourth chromosome between periods when the mean TE copy number remains fairly constant (Figure 1). This is in contrast to the freely recombining chromosomes, which maintained stable equilibrium copy numbers throughout the simulations, and the situation with strong synergism between elements, where no fixations were observed (Figure 1).
Figure 1.—
An example simulation run with weak (A) and strong (B) synergism when the fourth chromosome is completely nonrecombining. Diploid mean TE copy numbers are shown for the entire genome (thick black line), the nonrecombining fourth chromosome (thick gray line), and the three freely recombining chromosomes (thin black line) for simulation parameters N = 1000, u = 0.01, v = 0, a = 0.001, and b = 0.0003 (A) or b = 0.0006 (B).
Classical mutation models usually assume a uniform genomic mutation rate and a constant selection coefficient for new mutations, resulting in a constant expected speed of Muller's ratchet (e.g., Gordo and Charlesworth 2000, 2001; Stephan and Kim 2002). On the other hand, population genetic models of transposable elements generally assume a fixed rate of transposition per element (Le Rouzic and Deceliere 2005), leading to greater genomic transposition rates with higher TE copy numbers. To counter this potential proliferation, the fitness effects of each insertion must be a decreasing function of TE abundance (Charlesworth and Charlesworth 1983). Thus, with more elements, two antagonistic forces can act: the ratchet may be either accelerated as a result of the increased genomic transposition rate or decelerated owing to stronger selection against insertions.
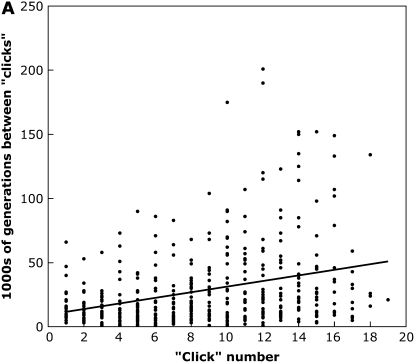
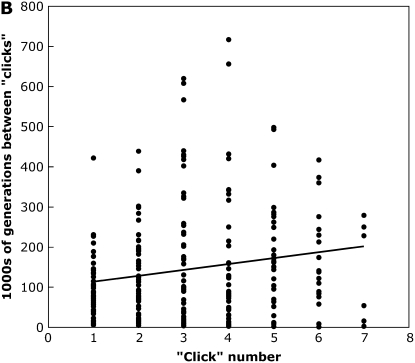
Under the quadratic fitness equation used here, we found that the time between successive fixations generally increased as copy number increased, indicating that Muller's ratchet slows down as more elements accumulate on the nonrecombining chromosome, and suggesting that the effects of stronger selection outweigh the higher genomic transposition rate (Figure 2). For example, for the two sets of parameters investigated in Figure 2, we performed a least-squares linear regression of time between fixations and “click” number, and found significantly positive slopes (Figure 2A, F1,465 = 56.3, P < 0.0001; Figure 2B, F1,209 = 7.42, P = 0.007). Our analysis is different from Gordo and Charlesworth's (2001) model of Muller's ratchet and transposable elements, as they essentially modified a mutational model to fit estimates of constant genomic transposition rates and assumed multiplicative fitness effects. However, it is consistent with an asexual mutational model that found that Muller's ratchet can effectively be halted if deleterious mutations have synergistic fitness effects (Kondrashov 1994; but see Butcher 1995), although in our model we never observed the fourth chromosome to reach a stable equilibrium copy number in simulations where TE fixations occurred, even over millions of generations (which equates to hundreds of millions of generations after scaling the parameters appropriately).
Figure 2.—
The time between clicks of the ratchet as a function of the ratchet number for simulations with a completely nonrecombining fourth chromosome for simulation parameters: N = 1000, u = 0.01, v = 0, a = 0.001, and b = 0.0003 (A) or b = 0.0004 (B). A shows the results of 30 simulations run for 5 × 105 generations, and B shows the results of 50 simulations run for 106 generations. The line shows the least-squares linear regression.
If we ignore the fact that the rate of Muller's ratchet is not constant, for the sake of comparison, and simply calculate a mean number of fixations per generation across the entire length of the simulation run, we have a rough measure with which to compare the speed with which TEs accumulate under different parameter conditions. Table 1 shows this average rate of fixation on the fourth chromosome under a range of synergism coefficients for two population sizes. As in Figure 1, it can be seen that element fixation was much more prevalent when synergism was weak (i.e., b was small). For a given strength of synergism, element fixation was also more likely to occur when populations were smaller, and fixations tended to be more rapid in smaller populations. We also considered the situation when local recombination was reduced but not completely absent. When the recombination frequency on the fourth chromosome was 10-fold lower than the rest of the genome (r = 10−4 between any two insertion sites, resulting in one crossover event per fourth chromosome every ∼30 generations on average), no fixations were ever observed for any set of parameters tested (results not shown). With a 100-fold lower recombination frequency on the fourth chromosome (r = 10−5 between any two insertion sites, resulting in one crossover event per fourth chromosome every ∼300 generations on average), element accumulation was widespread, but occurred at a considerably slower rate than in the complete absence of recombination (Table 1).
TABLE 1.
The speed of Muller's ratchet on a null- or low-recombining chromosome
| Null recombination
|
Low recombination
|
|||||||
|---|---|---|---|---|---|---|---|---|
|
N = 1000
|
N = 500
|
N = 1000
|
N = 500
|
|||||
| b | Clicks | Runs | Clicks | Runs | Clicks | Runs | Clicks | Runs |
| 0.0002 | 39.4 | 20a | — | 12.9 | 10b | — | ||
| 0.0003 | 3.1 | 30c | — | 0.50 | 10 | 9.95 | 10b | |
| 0.0004 | 0.49 | 50 | 7.4 | 20b | 0.03 | 10 | 1.34 | 10 |
| 0.0005 | 0.12 | 30 | 1.86 | 10c | 0 | 10 | 0.55 | 10 |
| 0.0006 | 0.01 | 30 | 0.62 | 10 | 0.22 | 10 | ||
| 0.0007 | 0 | 10 | 0.34 | 10 | 0.13 | 10 | ||
| 0.0008 | 0.15 | 10 | 0.02 | 10 | ||||
| 0.0009 | 0.17 | 10 | ||||||
The average number of clicks per 105 generations is shown, assuming a constant rate of element fixation, with the recombination rate on the fourth chromosome either 0 (null recombination) or 10−5 between insertion sites (low recombination). The remaining parameters are u = 0.01, v = 0, a = 0.001.
All simulations are run for 106 generations, except where indicated. — denotes simulations where element fixation was so rapid that the computing power was insufficient to run the simulation for 105 generations.
105 generations.
2 × 105 generations.
5 × 105 generations.
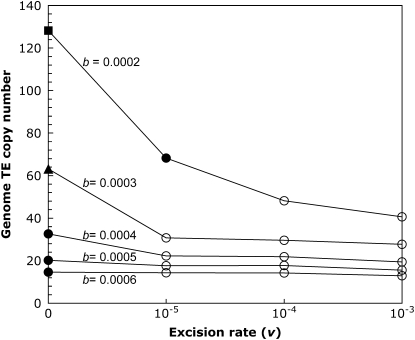
Our model thus far has assumed no element excision; therefore, once an element becomes fixed, Muller's ratchet has clicked irreversibly. While this lack of excision may be true for some classes of retrotransposons, which show little or no excision, the cut-and-paste transposition mechanism of DNA-based elements often leads to frequent element loss (Craig et al. 2002; Hua-Van et al. 2005). We incorporated excision into our model, and inspected the effects of excision rates one to three orders of magnitude below the rate of transposition for a genome with a completely nonrecombining fourth chromosome. For most parameter combinations tested, the presence of element excision halted the process of Muller's ratchet (Figure 3). Although temporary fixations were observed, these elements eventually became excised, allowing the population to reach a stable equilibrium close to that predicted by Equation 2. Only when the rate of fixation was much greater than the rate of excision did Muller's ratchet outpace excision, leading to continual element accumulation on the fourth chromosome (i.e., with b = 0.0002 and v = 10−5, see Figure 3).
Figure 3.—
The effect of excision on element abundance. The mean genome TE copy number at the end of the simulation is shown for simulations with a completely nonrecombining fourth chromosome for a range of synergism coefficients and excision rates, and the remaining simulation parameters were held constant: N = 1000, u = 0.01, a = 0.001. Simulations were run for 106 generations (denoted by circles), except for the triangle (5 × 105 generations) and the square (105 generations). Open circles indicate simulations that reached stable transposition–excision–selection equilibria, and solid symbols indicate simulations where fixations leading to nonequilibrium dynamics were observed. All data points are based on at least 10 simulation runs.
DISCUSSION
Many authors have suggested that the reduction in the pressure of selection against TEs when recombination is reduced can lead to the buildup of elements in low recombination regions (e.g., Charlesworth and Langley 1991; Duret et al. 2000; Bartolomé et al. 2002; Rizzon et al. 2002; Fontanillas et al. 2007); here we provide the first theoretical analysis of this situation. We have shown that accumulation of TEs under the deleterious insertion model is expected to occur only in the genomes of small populations where recombination is severely reduced, when excision is extremely rare or absent, and with weak synergism between elements. These criteria should be empirically testable, yet might be satisfied only under a very limited range of biological circumstances. This is in contrast to the ectopic exchange model, which broadly predicts that the number of TE insertions is inversely related to the recombination rate, even in very large populations (Langley et al. 1988; Montgomery et al. 1991; Charlesworth et al. 1992). Therefore, if TE accumulation is observed in low recombination regions, but the conditions necessary for buildup under the deleterious insertion model are not met, we can infer that the ectopic exchange model is implicated. Our model thus provides a first step in distinguishing between the leading models of TE distribution and abundance in regions of different recombination.
The effects of recombination on the deleterious insertion model were previously investigated only without any variation in recombination rate across the genome. Charlesworth and Charlesworth (1983) identified only minor effects of the recombination rate on TE abundance, and Dolgin and Charlesworth (2006) found large effects of the complete absence of recombination with asexuality, but no theoretical study has considered chromosomal regions with different recombination rates. This is important, because differences in the local recombination rate can drastically influence the effective population size experienced by insertions, as a result of the Hill–Robertson effects (Hill and Robertson 1966; Felsenstein 1974). The importance of effective population size for the abundance of TEs in general was first noted by Charlesworth and Charlesworth (1983), who found that smaller populations led to slightly greater equilibrium TE copy numbers in the presence of recombination. Later studies showed that small population size with sexual reproduction can often lead to unlimited increases in copy number, especially with high selfing rates, but the population sizes involved in such situations were unrealistically small for most natural populations (Brookfield and Badge 1997; Wright and Schoen 1999).
Here we have used large, randomly mating populations that may be more representative of natural populations of organisms like Drosophila, focusing on TEs with weak fitness effects that can segregate in noncoding regions. We found that Hill–Robertson effects in low recombination regions can lead to stochastic TE accumulation. Even so, the population sizes used in this study are still probably smaller than those found in nature for Drosophila populations. Most of our simulations involved a population size of N = 103, which reflects a size of 105 following the scaling employed here (see methods). This is an order of magnitude lower than the effective population size of 106 typically assumed for D. melanogaster (Kreitman 1983). Simulations run with larger populations indicated that TE accumulation was less likely and/or occurred at a slower rate (results not shown), but these simulations were too slow and computationally intensive to replicate many times. The possibility of TE accumulation in natural populations could thus be more limited than the already restrictive set of circumstances identified in our model, where larger population sizes reduce Hill–Robertson effects. On the other hand, our model did not consider other factors that might reduce the effective population size and potentially accelerate the rate of ratchet, such as population subdivision (Combadão et al. 2007) or effects of background selection and selective sweeps at linked coding or regulatory sites (Gordo and Charlesworth 2001). The latter effect could well be very important for nonrecombining genomic regions like the fourth chromosome (Sheldahl et al. 2003) and the neo-Y chromosome of D. miranda (Bachtrog 2003), where DNA sequence diversity is lower than the genomewide average by more than a factor of 10, implying a large reduction in effective population size.
Another problem in relating our results to Drosophila data is that the nonrecombining fourth chromosome in our model represented 10% of the genome. In reality, however, the fourth chromosome is much smaller. When we adjusted the chromosome sizes and made the fourth chromosome occupy only 1% of the genome, TE accumulation was never observed under any of the parameter conditions permitting accumulation on the larger chromosome that we used (results not shown). This suggests that selection is more effective at preventing TE buildup when the insertion rate of new elements into nonrecombining regions is lower, consistent with general Muller's ratchet theory that fixations occur more rapidly with greater mutation rates (Gordo and Charlesworth 2000). Although we exaggerated the size of the fourth chromosome, a larger chromosome might more accurately approximate other nonrecombining chromosomes including sex chromosomes, such as the neo-Y chromosome in D. miranda, which is riddled with TEs (Steinemann and Steinemann 1998; Bachtrog 2003). Our model also considered only genomic element copy numbers in the tens to hundreds, but the total number of active elements in the Drosophila genome is probably about an order of magnitude greater (Bartolomé et al. 2002; Kaminker et al. 2002; Bergman et al. 2006). However, given the inflated size of the fourth chromosome in our simulations, the reduced genomic copy number counterbalances the enlarged chromosome size and makes the rate of new insertions into the fourth chromosome reasonably realistic.
The results of Gordo et al. (2002) show that, when Muller's ratchet operates, the effect of deleterious mutations on neutral diversity in nonrecombining genomic regions is less than that predicted by equilibrium background selection theory. We have argued that the ratchet is unlikely to be causing a buildup of TEs on the fourth chromosome of D. melanogaster. It follows that their effect on neutral diversity should be adequately predicted by the background selection formula if TEs are contained by selection against the deleterious effects of element insertions on fitness (Charlesworth 1996). But the predicted reduction in diversity due to background selection effects from the observed number of segregating TEs on the fourth chromosome is at least a factor of 1000-fold (Charlesworth 1996; Carr et al. 2001), compared with an observed autosome to fourth chromosome silent diversity ratio of about 20 for D. melanogaster (Sheldahl et al. 2003). This suggests that, as noted by Charlesworth (1996), the background selection model greatly overpredicts the reduction in diversity. One possibility is that element insertions outside coding sequences are largely neutral on the fourth chromosome, due to the absence of meiotic ectopic exchange. These elements would not, therefore, exert background selection effects. This faces the difficulty, however, that retrotranspons do not show evidence for accumulation on the fourth chromosome (Bartolomé et al. 2002; Kaminker et al. 2002; Bergman et al. 2006), as we would expect with this hypothesis. The solution to this dilemma may be that many members of this element class appear to have invaded D. melanogaster recently, and have not yet had time to accumulate on the fourth chromosome (Sánchez-Garcia et al. 2005; Bergman and Bensasson 2007).
Nonetheless, analyses of the D. melanogaster genome have revealed that many families of TEs, including both DNA-based elements and retrotransposons, tend to accumulate in euchromatic and heterochromatic regions where recombination is reduced (Bartolomé et al. 2002; Kaminker et al. 2002; Rizzon et al. 2002; Bergman et al. 2006; Fontanillas et al. 2007), but the nature of the mechanisms involved is obscure. The results of our model indicate that TE accumulation under the deleterious insertion model is expected only when element excision is absent or extremely rare. Because DNA transposons can excise from the genome, albeit at a low rate (Nuzhdin and Mackay 1995; Suh et al. 1995; Vieira and Biémont 1997; Pasyukova et al. 1998; Maside et al. 2000), Muller's ratchet is likely to be ineffective for this class of elements. It thus seems more likely that the ectopic exchange model explains the Drosophila data, because the nonrecombining fourth chromosome is enriched in DNA-based elements with the ability to excise (Bartolomé et al. 2002; Kaminker et al. 2002; Bergman et al. 2006). This is further supported by the observation that the density of DNA transposons parallels the recombination rate along the chromosomes (Rizzon et al. 2002), whereas our model shows that low to moderate amounts of recombination effectively prevent elements from accumulating.
Unlike DNA-based elements, retrotransposons rarely excise from the genome (Craig et al. 2002; Hua-Van et al. 2005) and tend to be fairly homogenously distributed, except for accumulation in some regions with extremely low recombination rates (Rizzon et al. 2002; but see Bartolomé et al. 2002). Recent analyses have also demonstrated that these elements are often fixed within populations in nonrecombining portions of the Drosophila genome (Bachtrog 2003; Bartolomé and Maside 2004; Maside et al. 2005). Bartolomé and Maside (2004) used a PCR-based approach to determine the population frequency of a number of TE insertions in regions of suppressed or free recombination. They found that elements in regions of high recombination segregated at low frequencies and tended to be young, whereas null recombination regions were enriched in old elements at high frequencies or fixation, including several retrotransposons. This is at least qualitatively consistent with a model of retrotransposons accumulating and becoming fixed in low recombination regions due to Muller's ratchet. However, this model would also predict accumulation of retrotransposons on the fourth chromosome; as discussed above, this is not the case. The presence of fixed TEs is nonetheless compatible with the ectopic exchange model, because neutral elements can drift to high frequencies and fixation in low recombination regions, given that these regions have small effective population sizes.
DNA-based elements and retrotransposons show many differences in their respective intragenomic dynamics and distributions, and the causes of these differences remain unclear (Hua-Van et al. 2005). Here we have shown that a selective mechanism that has often been suggested to explain the prevalence of TEs in regions of suppressed recombination can probably be ruled out for DNA-based elements, because they exhibit appreciable rates of element excision. The limited population survey data for retrotransposons in Drosophila is consistent with our model, but screening of more insertions in multiple populations will be needed to test whether fixations are in fact more prevalent in low recombination regions. With the sequencing of more D. melanogaster strains, we should be able to better understand the population level processes underlying our genomic observations. Although we have identified some necessary conditions for TEs to build up through Muller's ratchet, determining conclusively which selective mechanisms are involved in causing TEs to accumulate in low recombination regions of the genome requires more experimental and theoretical analyses.
Acknowledgments
We thank the members of the Ashworth Xgrid cluster for computing time, and L. Loewe for helpful comments on the manuscript. This work was supported by postgraduate research scholarships to E.S.D. from the Natural Sciences and Engineering Research Council (Canada) and the University of Edinburgh School of Biological Sciences. B.C. was supported by the Royal Society (United Kingdom).
References
- Adams, M. D., S. E. Celniker, R. A. Holt, C. A. Evans, J. D. Gocayne et al., 2000. The genome sequence of Drosophila melanogaster. Science 287 2185–2195. [DOI] [PubMed] [Google Scholar]
- Ashburner, M., K. G. Golic and R. S. Hawley, 2004. Drosophila: A Laboratory Handbook, Ed. 2. Cold Spring Harbor Laboratory Press, Cold Spring Harbor, NY.
- Bachtrog, D., 2003. Accumulation of Spock and Worf, two novel non-LTR retrotransposons, on the neo-Y chromosome of Drosophila miranda. Mol. Biol. Evol. 20 173–181. [DOI] [PubMed] [Google Scholar]
- Bartolomé, C., and X. Maside, 2004. The lack of recombination drives the fixation of transposable elements on the fourth chromosome of Drosophila melanogaster. Genet. Res. 83 91–100. [DOI] [PubMed] [Google Scholar]
- Bartolomé, C., X. Maside and B. Charlesworth, 2002. On the abundance and distribution of transposable elements in the genome of Drosophila melanogaster. Mol. Biol. Evol. 19 926–937. [DOI] [PubMed] [Google Scholar]
- Bergman, C. M., and D. Bensasson, 2007. Recent LTR retrotransposon insertion contrasts with waves of non-LTR insertion since speciation in Drosophila melanogaster. Proc. Natl. Acad. Sci. USA 104 11340–11345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergman, C. M., H. Quesneville, D. Anxolabéhère and M. Ashburner, 2006. Recurrent insertion and duplication generate networks of transposable element sequences in the Drosophila melanogaster genome. Genome Biol. 7 R112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biémont, C., A. Tsitrone, C. Vieira and C. Hoogland, 1997. Transposable element distributions in Drosophila. Genetics 147 1997–1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookfield, J. F. Y., 1991. Models of repression of transposition in P-M hybrid dysgenesis by P cytotype and by zygotically encoded repressor proteins. Genetics 128 471–486. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brookfield, J. F. Y., and R. M. Badge, 1997. Population genetic models of transposable elements. Genetica 100 281–294. [PubMed] [Google Scholar]
- Butcher, D., 1995. Muller's ratchet, epistasis, and mutation effects. Genetics 141 431–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carr, M., J. R. Soloway, T. E. Robinson and J. F. Y. Brookfield, 2001. An investigation of the cause of low variability on the fourth chromosome of Drosophila melanogaster. Mol. Biol. Evol. 18 2260–2269. [DOI] [PubMed] [Google Scholar]
- Casals, F., J. González and A. Ruiz, 2006. Abundance and chromosomal distribution of six Drosophila buzzatii transposons: BuT1, BuT2, BuT3, BuT4, BuT5, and BuT6. Chromosoma 115 403–412. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., 1990. Mutation-selection balance and the evolutionary advantage of sex and recombination. Genet. Res. 55 199–221. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., 1996. Background selection and patterns of genetic diversity in Drosophila melanogaster. Genet. Res. 68 131–149. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., and D. Charlesworth, 1983. The population dynamics of transposable elements. Genet. Res. 42 1–27. [Google Scholar]
- Charlesworth, B., and C. H. Langley, 1991. Population genetics of transposable elements in Drosophila, pp. 150–176 in Evolution at the Molecular Level, edited by R. K. Selander, A. G. Clark and T. S. Whittam. Sinauer Associates, Sunderland, MA.
- Charlesworth, B., A. Lapid and D. Canada, 1992. The distribution of transposable elements within and between chromosomes in a population of Drosophila melanogaster. II. Inferences on the nature of selection against elements. Genet. Res. 60 115–130. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., P. Sniegowski and W. Stephan, 1994. The evolutionary dynamics of repetitive DNA in eukaryotes. Nature 371 215–220. [DOI] [PubMed] [Google Scholar]
- Charlesworth, B., C. H. Langley and P. D. Sniegowski, 1997. Transposable element distributions in Drosophila. Genetics 147 1993–1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Combadão, J., P. R. A. Campos, F. Dionisio and I. Gordo, 2007. Small-world networks decrease the speed of Muller's ratchet. Genet. Res. 89 7–18. [DOI] [PubMed] [Google Scholar]
- Comeron, J. M., and M. Kreitman, 2002. Population, evolutionary and genomic consequences of interference selection. Genetics 161 389–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Craig, N. L., R. Craigie, M. Gellert and A. M. Lambowitz (Editors), 2002. Mobile DNA II. ASM, Washington, DC.
- Dolgin, E. S., and B. Charlesworth, 2006. The fate of transposable elements in asexual populations. Genetics 174 817–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doolittle, W. F., and C. Sapienza, 1980. Selfish genes, the phenotype paradigm and genome evolution. Nature 284 601–603. [DOI] [PubMed] [Google Scholar]
- Duret, L., G. Marais and C. Biémont, 2000. Transposons but not retrotransposons are located preferentially in regions of high recombination rate in Caenorhabditis elegans. Genetics 156 1661–1669. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eanes, W. F., C. Wesley and B. Charlesworth, 1992. Accumulation of P elements in minority inversions in natural populations of Drosophila melanogaster. Genet. Res. 59 1–9. [DOI] [PubMed] [Google Scholar]
- Ewens, W. J., 2004. Mathematical Population Genetics, Ed. 2. Springer-Verlag, Berlin.
- Felsenstein, J., 1974. The evolutionary advantage of recombination. Genetics 78 737–756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Finnegan, D. J., 1992. Transposable elements, pp. 1096–1107 in The Genome of Drosophila melanogaster, edited by D. L. Lindsley and G. Zimm. Academic Press, New York.
- Fontanillas, P., D. L. Hartl and M. Reuter, 2007. Genome organization and gene expression shape the transposable element distribution in the Drosophila melanogaster euchromatin. PLoS Genet. 3 e210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fullerton, S. M., A. Bernardo Carvalho and A. G. Clark, 2001. Local rates of recombination are positively correlated with GC content in the human genome. Mol. Biol. Evol. 18 1139–1142. [DOI] [PubMed] [Google Scholar]
- Goldman, A. S., and M. Lichten, 1996. The efficiency of meiotic recombination between dispersed sequences in Sacchromyces cerevisiae depends upon their chromosomal location. Genetics 144 43–55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goldman, A. S., and M. Lichten, 2000. Restriction of ectopic recombination by interhomolog interactions during Saccharomyces cerevisiae meiosis. Proc. Natl. Acad. Sci. USA 97 9537–9542. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordo, I., and B. Charlesworth, 2000. The degeneration of asexual haploid populations and the speed of Muller's ratchet. Genetics 154 1379–1387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gordo, I., and B. Charlesworth, 2001. The speed of Muller's ratchet with background selection and the degeneration of Y chromosomes. Genet. Res. 78 149–161. [DOI] [PubMed] [Google Scholar]
- Gordo, I., A. Navarro and B. Charlesworth, 2002. Muller's ratchet and the pattern of variation at a neutral locus. Genetics 161 835–848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hill, W. G., and A. Robertson, 1966. The effect of linkage on limits to artificial selection. Genet. Res. 8 269–294. [PubMed] [Google Scholar]
- Hoogland, C., and C. Biémont, 1996. Chromosomal distribution of transposable elements in Drosophila melanogaster: test of the ectopic recombination model for maintenance of insertion site number. Genetics 144 197–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hua-Van, A., A. Le Rouzic, C. Maisonhaute and P. Capy, 2005. Abundance, distribution and dynamics of retrotransposable elements and transposons: similarities and differences. Cytogenet. Genome Res. 110 426–440. [DOI] [PubMed] [Google Scholar]
- Kaminker, J. S., C. M. Bergman, B. Kronmiller, J. Carlson, R. Svirskas et al., 2002. The transposable elements of the Drosophila melanogaster euchromatin: a genomics perspective. Genome Biol. 3 RESEARCH0084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keightley, P. D., and S. P. Otto, 2006. Interference among deleterious mutations favours sex and recombination in finite populations. Nature 443 89–92. [DOI] [PubMed] [Google Scholar]
- Kidwell, M. G., 2002. Transposable elements and the evolution of genome size in eukaryotes. Genetica 115 49–63. [DOI] [PubMed] [Google Scholar]
- Kondrashov, A. S., 1994. Muller's ratchet under epistatic selection. Genetics 136 1469–1473. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kreitman, M., 1983. Nucleotide polymorphism at the alcohol dehydrogenase locus of Drosophila melanogaster. Nature 304 412–417. [DOI] [PubMed] [Google Scholar]
- Langley, C. H., E. A. Montgomery, R. Hudson, N. Kaplan and B. Charlesworth, 1988. On the role of unequal exchange in the containment of transposable element copy number. Genet. Res. 52 223–235. [DOI] [PubMed] [Google Scholar]
- Le Rouzic, A., and G. Deceliere, 2005. Models of the population genetics of transposable elements. Genet. Res. 85 171–181. [DOI] [PubMed] [Google Scholar]
- Le Rouzic, A., T. S. Boutin and P. Capy, 2007. Long-term evolution of transposable elements. Proc. Natl. Acad. Sci. USA 104 19375–19380. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lynch, M., 2007. The Origins of Genome Architecture. Sinauer Associates, Sunderland, MA.
- Maside, X., S. Assimacopoulos and B. Charlesworth, 2000. Rates of movement of transposable elements on the second chromosome of Drosophila melanogaster. Genet. Res. 75 275–284. [DOI] [PubMed] [Google Scholar]
- Maside, X., C. Bartolomé, S. Assimacopoulos and B. Charlesworth, 2001. Rates and movement of transposable elements on the second chromosome of Drosophila melanogaster: in situ hybridization versus Southern blotting data. Genet. Res. 78 121–136. [DOI] [PubMed] [Google Scholar]
- Maside, X., S. Assimacopoulos and B. Charlesworth, 2005. Fixation of transposable elements in the Drosophila melanogaster genome. Genet. Res. 85 195–203. [DOI] [PubMed] [Google Scholar]
- Matsumoto, M., and T. Nishimura, 1998. Mersenne twister: a 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Mod. Comput. Simul. 8 3–30. [Google Scholar]
- McVean, G. A. T., and B. Charlesworth, 2000. The effects of Hill–Robertson interference between weakly selected mutations on patterns of molecular evolution and variation. Genetics 155 929–944. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Montgomery, E. A., B. Charlesworth and C. H. Langley, 1987. A test for the role of natural selection in the stabilization of transposable element copy number in a population of Drosophila melanogaster. Genet. Res. 49 31–41. [DOI] [PubMed] [Google Scholar]
- Montgomery, E. A., S. M. Huang, C. H. Langley and B. H. Judd, 1991. Chromosome rearrangement by ectopic recombination in Drosophila melanogaster: genome structure and evolution. Genetics 129 1085–1098. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muller, H. J., 1964. The relation of recombination to mutational advance. Mutat. Res. 1 2–9. [DOI] [PubMed] [Google Scholar]
- Nuzhdin, S. V., 1999. Sure facts, speculations, and open questions about evolution of transposable elements. Genetica 107 129–137. [PubMed] [Google Scholar]
- Nuzhdin, S. V., and T. F. C. Mackay, 1995. The genomic rate of transposable element movement in Drosophila melanogaster. Mol. Biol. Evol. 12 180–181. [DOI] [PubMed] [Google Scholar]
- Orgel, L. E., and F. H. Crick, 1980. Selfish DNA: the ultimate parasite. Nature 284 604–607. [DOI] [PubMed] [Google Scholar]
- Pasyukova, E. G., S. V. Nuhzdin and D. A. Filatov, 1998. The relationship between the rate of transposition and transposable element copy number for copia and Doc retrotransposons of Drosophila melanogaster. Genet. Res. 72 1–11. [DOI] [PubMed] [Google Scholar]
- Rizzon, C., G. Marais, M. Gouy and C. Biemont, 2002. Recombination rate and the distribution of transposable elements in the Drosophila melanogaster genome. Genome Res. 12 400–407. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sánchez-Garcia, A., X. Maside and B. Charlesworth, 2005. High rate of horizontal transfer of transposable elements in Drosophila. Trends Genet. 21 200–203. [DOI] [PubMed] [Google Scholar]
- Sheldahl, L. A., D. M. Weinreich and D. M. Rand, 2003. Recombination, dominance and selection on amino acid polymorphism in the Drosophila genome: contrasting patterns on the X and fourth chromosomes. Genetics 165 1195–1208. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sniegowski, P., and B. Charlesworth, 1994. Transposable element numbers in cosmopolitan inversions from a natural population of Drosophila melanogaster. Genetics 137 815–827. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Söderberg, R. J., and O. G. Berg, 2007. Mutational interference and the progression of Muller's ratchet when mutations have a broad range of deleterious effects. Genetics 177 971–986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Steinemann, M., and S. Steinemann, 1998. Enigma of Y chromosome degeneration: neo-Y and neo-X chromosomes of Drosophila miranda a model for sex chromosome evolution. Genetica 102/103 409–420. [PubMed] [Google Scholar]
- Stephan, W., and Y. Kim, 2002. Recent applications of diffusion theory to population genetics, pp. 72–93 in Modern Developments in Theoretical Population Genetics, edited by M. Slatkin and M. Veuille. Oxford University Press, Oxford.
- Suh, D. S., E. H. Choi, T. Yamazaki and K. Harada, 1995. Studies on the transposition rates of mobile genetic elements in a natural population of Drosophila melanogaster. Mol. Biol. Evol. 12 748–758. [DOI] [PubMed] [Google Scholar]
- Vieira, C., and C. Biémont, 1997. Transposition rate of the 412 retrotransposable element is independent of copy number in natural populations of Drosophila simulans. Mol. Biol. Evol. 14 185–188. [DOI] [PubMed] [Google Scholar]
- Wright, S. I., and D. J. Schoen, 1999. Transposon dynamics and the breeding system. Genetica 107 139–148. [PubMed] [Google Scholar]