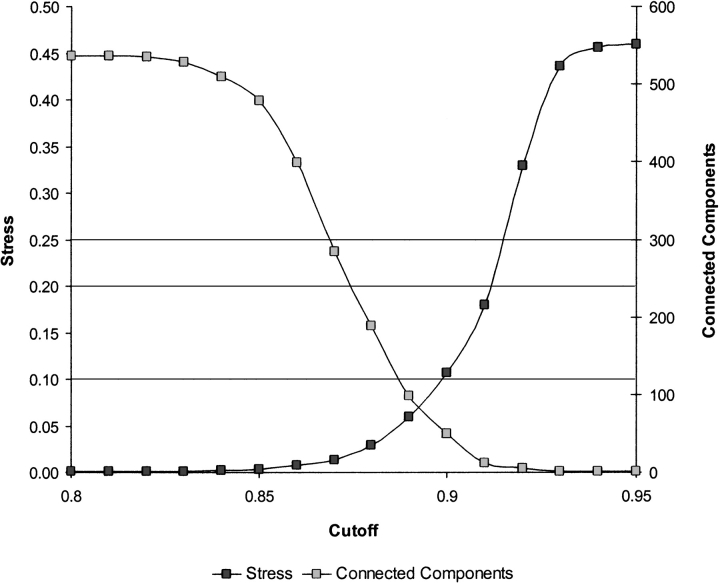
Figure 2.

Stress and number of connected components of the 2D SPE map of the Manning kinase superfamily as a function of the neighborhood radius, r_c. For a well-sampled noiseless manifold embedded in the intrinsic dimension, the ideal cutoff is any value that leads to zero stress and a single connected component. For sparsely sampled data sets that contain discontinuities (such as the ones examined here), no such value exists, and the “ideal” cutoff is one that represents a good compromise between the stress and the number of connected components, and leads to a visually meaningful map. This value is typically located near the point where the two normalized curves intersect.