Strained DNA is kinked by low concentrations of Zn²⁺

Abstract

A novel atomic force microscope with a magnetically oscillated tip has provided unprecedented resolution of small DNA fragments spontaneously adsorbed to mica and imaged in situ in the presence of divalent ions. Kinks (localized bends of average angle 78°) were observed in axially strained minicircles consisting of tandemly repeated d(A)₅ and d(GGGCC[C]) sequences. The frequency of kinks in identical minicircles increased 4-fold in the presence of 1 mM Zn²⁺ compared with 1 mM Mg²⁺. Kinking persisted in mixed Mg²⁺/Zn²⁺ electrolytes until the Zn²⁺ concentration dropped below 100 μM, indicating that this type of kinking may occur under physiological conditions. Kinking appears to replace intrinsic bending, and statistical analysis shows that kinks are not localized within any single sequence element. A surprisingly small free energy is associated with kink formation.

DNA bending, both intrinsic and protein-induced, plays an important role in the control of gene expression, replication, recombination, and packaging in the nucleus (1–4). Kinking as a distinct category of DNA bending was first proposed as a possible mechanism for wrapping DNA around nucleosomal proteins (5–7) but later proved to be a more general phenomenon in specific protein–DNA complexes (8–11). Methods for detecting structural fluctuations in DNA are abundant (12–19), but without adequate high-resolution data, discriminating between smoothly distributed bending and highly localized stereochemical kinks is not possible. To study such localized structural features in DNA, a resolution on the order of at least 1 nm is required.

Scanning probe microscopy has become an important new tool in structural biology (20). In particular, the atomic force microscope (AFM) is capable of imaging at near-atomic resolution and under physiological conditions (21) and so should, in principle, be useful for in situ imaging of conformational changes in DNA molecules. In the past, however, due to tip broadening effects, AFM images of DNA have been limited to at least several nanometers in width (22, 23), except in dense aggregates where the helix pitch has been resolved (24). We have employed a novel magnetically driven oscillating-probe AFM (25) that operates at significantly smaller amplitudes than used in fluid tapping mode (23, 26). By using it, we can image gently bound molecules at much higher resolution (about 1 nm), probably because fine asperities are preserved on the probe that serve as extremely sharp AFM scanning tips (25).

We have used this new microscope to study DNA microcircles constructed from phased sequence motifs known to bend DNA. T4 ligase-mediated ligation was used to produce both linear DNA oligomers and microcircles from tandem repeats of alternating sequence elements d(A)₅ and d(GGGCC[C]), the only elements presently known that confer substantial static bending in DNA (27–34). This combination of sequences forms an axial bend of at least 30° per helical turn (34). In circles consisting of 16 helical turns, we found two quite distinct types of bending: one was smooth, and the other was sharp and localized, typically much greater than 45° over a distance smaller than our best resolution (about 1 nm) (35). We define the latter as kinks.

Microcircles consisting of 12 helical turns of DNA are essentially unstrained because their natural static curvature sums to approximately 360°. Circles containing 16 turns of DNA are axially strained, however, because the average static bending exceeds 360° and a thermal fluctuation is required for their ends to become ligated. In this report, we show that unstrained 12-turn microcircles do not form kinks under any ionic conditions tested but that the DNA in strained 16-turn microcircles can kink in the presence of Zn²⁺ ions, suggesting that both axial strain and a threshold Zn²⁺ ion concentration are required for the kinking phenomenon to occur. We also describe measurements of the kinking frequency, the distribution of kink angles, and the intervals between kinks. Finally, we investigated this phenomenon in mixed electrolytes (Mg²⁺/Zn²⁺) that span a range of concentrations likely to include physiologically relevant conditions.

MATERIALS AND METHODS

Sample Preparation.

The following 42-bp sequence was used for ligation:

CCCAAAAAGGGCCAAAAAGGGCCCAAAAAGGGCCAAAAAGGG

  TTTTTCCCGGTTTTTCCCGGGTTTTTCCCGGTTTTTCCCGGG

Two-dimensional gels were used to separate linear and circular molecules (32, 33). The relative cyclization efficiencies for all circles were obtained from steady-state ligation as described (32). Maximum circle formation occurs for oligomers of 126 bp, although some circles were also detected at a smaller size (34). The relative cyclization efficiency falls by a factor of 2 for the next larger circle of 168 bp (1.32 for 126-bp circles and 0.65 for 168-bp circles). This suggests that 126-bp circles are in a more favorable conformation for ligation due to their intrinsic bending properties, whereas 168-bp circles form superhelices and have to open out to bring their ends into position for ligation. The latter leads to a difference in strain energy between the two circles.

DNA molecules isolated from the gel were treated several times with isoamyl alcohol to remove the traces of chloroquine phosphate, an intercalating agent that imposes differential mobility on linear and circular species in the gel (36). Circular DNA molecules were subsequently ligated overnight to seal those with single-strand breaks (nicks), as they constitute a part of the total population of circles in the initial preparation (33, 34). Finally, both linear and circular molecules were passed at least three times through Sephadex NAP-10 columns (Pharmacia) and were kept dry until preparation for imaging.

AFM Imaging.

DNA samples were diluted to a final concentration of 0.5 μg/ml in electrolytes made from ultrafiltered water from a bioresearch grade Nanopure system and MgCl₂ and/or ZnBr₂. About 100 μl of the solution was placed onto freshly cleaved mica in the liquid cell of a PicoSPM (Molecular Imaging, Tempe, AZ). DNA adsorbed spontaneously onto the mica in the presence of Zn²⁺ and was stable under repeated scanning in the electrolyte with no intermediate drying, similar to the results reported by others (37). We believe that we are able to image DNA that is bound to the surface more gently by using magnetic A/C mode AFM (MAC Mode) (25) because of the much weaker interaction between the scanning probe and the sample compared with other scanning modes. When the microscope was operated in MAC mode with samples initially deposited in the presence of Zn²⁺ alone or in Zn²⁺/Mg²⁺ mixtures, we could always detect kinks. However, when we allowed DNA to bind to mica in Mg²⁺ alone and Zn²⁺ was subsequently added during the course of a scan, we could not induce kinking in the strained microcircles even at Zn²⁺ concentrations that led to marked kinking in the zinc-deposited experiments (data not shown). Thus, although DNA binding to the mica is presumably more gentle in these studies than in other techniques used to date for immobilizing DNA, it is still strong enough to prevent kinking once the molecules have been deposited on the substrate. Consequently, the role of the substrate in these experiments cannot be ignored.

Length Measurements and Spectral Analysis.

The results presented herein were duplicated on each sample a minimum of four times and the data were pooled to obtain the statistics. Length measurements were performed on calibrated images by using the public domain software nih image version 1.60. DNA widths were determined directly by using nanoscope iii software. The major sources of error in length measurements are due to scanner nonlinearities (not corrected for by calibration), the finite resolution of the instrument, and drift. We used both the mica atomic lattice and a standard calibration grating to calibrate the instrument and believe that calibration errors are less than 2%. Measurement uncertainties due to drift are about 5% in the worst case and these are uncorrelated with calibration errors, leading to a total uncertainty of 5.4%. Errors due to the finite resolution of the instrument become significant when measuring short distances (e.g., the interval between kinks). We obtained some measure of these uncertainties by making repeated measurements of the same sets of data, using the standard deviation in the redundant set as a measure of this uncertainty. We repeated measurements of 300 intervals five times and included another set of 160 intervals.

Of particular interest was the possibility that the kinks are correlated with particular sequence elements in the DNA and are, therefore, spaced by some multiple of a helix repeat (or half a helical repeat). Fast Fourier transform was used to obtain the power spectrum of the set of intervals between kinks (38). We calibrated the sensitivity of this approach with a real data set modified by a computer so that the intervals were forced to be multiples of a helix turn. This strictly periodic data were then distributed randomly with a Gaussian distribution to simulate ever decreasing resolution, taking the power spectrum at each step increase in the width of the random distribution. The peaks in the power spectrum persisted even when the width of the random distribution greatly exceeded one helical turn, which means that any existing periodicity would have been observed despite measurement errors. Our simulations, however, were used to rule out only a strict periodicity. If Zn²⁺ binds to a specific base (e.g., guanine), it is possible that further broadening of the distribution (beyond that of finite resolution) by random kinking at any one of the guanine bases would go undetected in this analysis.

RESULTS

We show examples of the 168-bp circles in 1 mM MgCl₂ in Fig. 1A and in 1 mM ZnBr₂ in Fig. 1B. These data are similar to those reported elsewhere (35), and they illustrate DNA images with a full width at half height (FWHH) of less than 3.5 nm. In all image fields, finding regions where features appear to be unusually narrow is generally possible, but we believe that this is not a valid approach for determining the overall instrumental resolution. Herein, we measured the FWHH across all parts of the images shown, averaging to produce a final result. By using this procedure, we find that our instrumental broadening is only a little more than 1 nm on average. It should be noted that helical turns have been observed in dense aggregates of DNA where the tip is presumably prevented from sampling the entire height of the molecules (24). High-resolution images of DNA were also obtained in propanol (39). However, we believe that the present level of resolution is unprecedented for images of isolated DNA molecules in aqueous solutions.

Figure 1.

DNA minicircles of 168 bp in 1 mM MgCl₂ (A) and 1 mM ZnBr₂ (B). (C) Circles of 126 bp in 1 mM ZnBr₂. (D) Linear 126-bp oligomers are shown in the same electrolyte. All four images are scaled as shown by the bar in D. Molecules were spontaneously adsorbed onto mica from solution and imaged in situ by using MAC mode AFM. The cantilever, with a spring constant 0.6 N/m, was oscillated at 5 nm p/p at 25 kHz and the set point decrease was 0.3 nm. The images (512 lines of data) were each acquired in 5 min.

As reported (35), the 168-bp circles in 1 mM Zn²⁺ look very different from their counterparts in 1 mM Mg²⁺. Instead of smoothly bending, they often consist of nearly straight sections of DNA connected by abrupt kinks (enlarged images are shown in ref. 35).

We counted 184 kinks in 205 molecules or ∼0.9 kinks per molecule for the axially strained 168-bp circles in 1 mM Mg²⁺. The same circles imaged in 1 mM Zn²⁺ on the same mica substrate yielded 621 kinks in 162 molecules or ∼3.8 kinks per molecule. We took precautions to ensure that ligation of the double helix was complete (see Sample Preparation). The above result, obtained with molecules from the same initial preparation, further suggests that the observed kinks cannot be attributed to nicks arising from incomplete ligation.

Images of the 126-bp circles in 1 mM Zn²⁺ are shown to the same scale in Fig. 1C. Their smaller size is evident, as is a comparative lack of kinking. We counted only 19 kinks in 116 molecules or 0.16 kinks per molecule. The images suggest that the molecules are somewhat elliptical in shape, but kinks are rarely observed. Since the sequences are identical to the 168-bp circles other than in size, this difference must be strain-related.

The linear DNA is more difficult to characterize because of its greater flexibility and its larger number of conformational degrees of freedom. Fig. 1D shows the linear 126-bp oligomer in 1 mM Zn²⁺. Linear, bent, and even circular forms are observed but kinks are rare.

It is important to determine whether kinks such as those observed in 1 mM Zn²⁺ might form under physiological conditions where both Zn²⁺ and Mg²⁺ are present. Fig. 2A shows images of the 168-bp circles in combined 10 mM Mg²⁺ and 1 mM Zn²⁺, which is reported to be approximately the physiological concentration of these ions (40). In a qualitative sense, kinks are present similarly to those observed in 1 mM Zn²⁺ only (Fig. 1B). The intracellular physiological activity of Zn²⁺ may be lower than 1 mM because of the sequestering of these ions by proteins. Fig. 2B shows images of the 168-bp circles that are still kinked in 100 μM Zn²⁺ and 1 mM Mg²⁺ although both kinked and circular molecules have been observed under these conditions. When the Zn²⁺ concentration is reduced to 50 μM in 1 mM Mg²⁺, very few kinked molecules remain and almost all are circular (Fig. 2C). Thus, the threshold for zinc-induced kinking evidently lies between these two values.

Figure 2.

Circles of 168 bp in 1 mM ZnBr₂/10 mM MgCl₂ (A), 0.1 mM ZnBr₂/1 mM MgCl₂ (B), and 0.05 mM ZnBr₂/1 mM MgCl₂ (C) showing a reduction in kink density as the concentration of Zn²⁺ is reduced. Imaging conditions are as described in Fig. 1.

There is considerable interest in the origin of the contrast in AFM images, for the measured height of DNA is rarely found close to the expected 2 nm (41, 42). In the present series of measurements, we found an interesting correlation between the amount of a given salt and the apparent contrast of the DNA. The contrast was greatest in 1 mM Mg²⁺ (1.7 nm) and smallest in the 10 mM Mg²⁺/1 mM Zn²⁺ (about 0.2 nm). Fig. 2 shows how contrast increases with decreasing zinc concentration. This suggests that adsorption of salt onto the surrounding substrate plays a significant role in AFM image contrast.

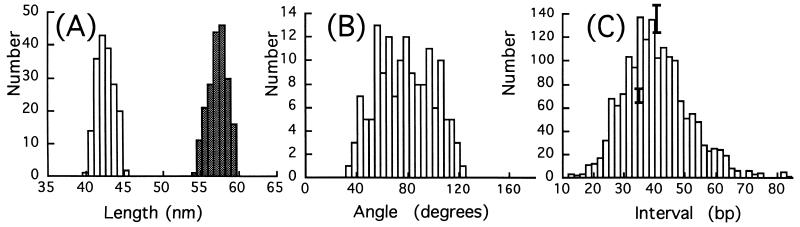
The high resolution of the microscope combined with the use of circular molecules permits comparatively accurate measurements of contour lengths. Data for 183 of the 126-bp circles and 197 of the 168-bp circles are summarized in the histogram shown in Fig. 3A. These data yield a rise per base of 0.34 ± 0.015 nm for both molecules, showing clearly that the DNA is in the B-form. There is no evidence of a population of shorter molecules due to a transition to A-form DNA, such as might be expected when molecules are dried onto a substrate for subsequent imaging.

Figure 3.

(A) Histograms of measured contour lengths for 126-bp circles (open bars) and 168-bp circles (cross-hatched bars). DNA lengths are 42.5 ± 1.1 and 57.3 ± 1.2 nm and correspond to the B-DNA conformation. (B) Histogram of the kink angles measured in 1 mM ZnBr₂. (C) Intervals (in bp) between pairs of kinks having the same direction with respect to the center of the circle. Error bars represent ±1 SD population, taking into account drift, calibration, and measurements errors.

Measured kink angles for 168-bp circles in 1 mM Zn²⁺ are summarized in Fig. 3B, where we have included all abrupt bends, including those that fall below our arbitrary cutoff of 45° for counting an abrupt bend as a kink. The distribution is broad, but there are very few abrupt bends of less than 45°. The average kink angle is 78 ± 22° (n = 150 kinks). As is clear from Fig. 1B, the residual curvature of the kinked DNA is greatly reduced and the number of kinks per circle (3.83) and their angles (nearly 80°) are almost large enough to be connected by straight DNA segments. Thus, relief of axial strain through kinking appears also to reduce static bending almost completely in these microcircles in the presence of Zn²⁺.

It would be of interest to know whether one part of the sequence is more likely to kink than another, but this cannot be determined directly because there are no reference points in the circles that can be identified at the available level of resolution. When only kinks that bend the helix in the same direction with respect to the center of the circle are taken into consideration, the fact that the sequence is repetitive and the kinks are constrained to lie in a plane (as the molecule is imaged) requires that interkink distances be multiples of a helical turn if the kinking locus is associated with a singular sequence element or with a structural feature such as major or minor groove. If kinking occurs into both grooves (or within both sequence elements used to make these circles), then the intervals between kinks would be required to be multiples of both helical turn and half a helical turn.

Our instrumental resolution is about half a helical turn, so to test the feasibility of this experiment, we simulated data as described in Materials and Methods. We broadened the simulated periodic data by 2, 4, 6, 8, and 10 bp (FWHH) by using a random number generator. We used a uniform random shifting of the data that models a Gaussian distribution to within 10% if we set DNA width equal to the width of the Gaussian. A recognizable peak persisted in the power spectrum out to 10 bp (FWHH) of random broadening, corresponding to about three times the measured instrumental broadening (data not shown).

The full set of measurements of the intervals between kinks that bend the helix axis in the same direction with respect to the center of the circle is shown in Fig. 3C. Also shown are some representative error bars showing plus and minus one standard deviation on the histogram bin height generated from redundant measurements on the same data sets as described in Materials and Methods. Clearly, within this uncertainty, there is no evidence of periodicity in these data. This is clearer still when the power spectrum of the data is calculated. The resulting Fourier spectrum showed a peak at the origin characteristic of 1/f noise, but there were no other periodic features (data not shown). Given the results of our simulations with broadened but periodic data sets, we must conclude that a fixed locus for these kinks (sequence or groove site) is most unlikely. The average distance between kinks is 40.5 ± 11 bp, indicating that the kinks tend to be spaced equidistantly (i.e., close to 168 bp per 3.83 kinks per circle).

We can estimate the free energy of formation for the kinks by assuming that the ratios of relative cyclization efficiencies for the two oligomers reflect stationary state population differences; i.e., the ratios of relative kinetic efficiencies under our experimental conditions are equal to the ratios of true cyclization probabilities. The cyclizations reported herein were conducted under conditions designed to meet this requirement by minimizing the kinetic effects of competition between elongation and cyclization (32, 43, 44). From the relative cyclization efficiencies (C_n) we obtain:

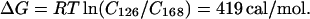Dividing by the average number of kinks per molecule yields ∼0.5 kcal/mol (1 cal = 4.184 J) in the presence of Mg²⁺, and 0.11 kcal/mol for Zn²⁺. Both values are at least one order of magnitude lower than previous estimates of kinking or bending in DNA based upon macroscopic continuum elastic theory and appropriate dynamic models for chain macromolecules. However, very recent results suggest that local DNA flexibility may be significantly greater than earlier values based upon classical elastic theory. Akiyama and Hogan (45) report a bending energy value of 0.4–0.9 kcal/mol for a 50° bend over 10 bp, in good agreement with the value estimated herein.

DISCUSSION

The strong enhancement of kinking observed herein in the presence of Zn²⁺ is consistent with earlier electron microscopy (46), electrooptical (47) and gel-mobility retardation studies (31). The solution studies of Nickol and Rau (47) suggested that the effects of Zn²⁺ persist even to lower concentrations (10 μM) than observed herein. However, since Zn²⁺ must interact strongly with the mica surface to play a role in binding the DNA, it is possible that the activity of Zn²⁺ may be reduced substantially near the mica surface, and therefore, our threshold estimate above must be considered an upper limit value. We note that intermediate concentrations of Zn²⁺ resulted in a mixed population of both circular and kinked molecules, an indication that the ion effect might vary smoothly with concentration.

The binding mechanism of the two ions to DNA is quite different. Zn²⁺ interacts predominantly with bases, whereas Mg²⁺ associates primarily with phosphates (47, 48). We observe that the action of Zn²⁺ is not inhibited by greatly increased Mg²⁺ concentration (Fig. 2A), a result that is consistent with different binding sites for the two ions. This provides further evidence that these kinks must be localized on the DNA since they require that the bases be exposed for interaction with Zn²⁺ (48). Our results with the unstrained circles (126 bp) show that an external stress (in the present case, axial strain) is also required for kinking. One might speculate therefore that supercoiled DNA or DNA stressed by protein–DNA interactions in chromatin or in regulatory complexes may be more susceptible to conformational transitions induced by Zn²⁺ and that this process may have a special role in triggering or facilitating transitions in chromatin structure or in transcriptional and other regulatory events.

Our estimate of free energy for DNA kinking is considerably lower than previous estimates obtained from classical calculations of kinking (6) or bending (5, 47, 49–51) energies for DNA, the latter based upon macroscopic continuum elastic theory (52) and the theory of the worm-like coil (53). The earlier estimates did not incorporate the effects of specific ion binding at the bases as is known to occur for both Mg²⁺ and Zn²⁺. The very recent results of Akiyama and Hogan (45, 54) suggest that DNA flexibility may be quite anisotropic and may occur over a range of sequence elements, thus permitting considerable DNA bending with energy costs similar to our estimate here. In the studies reported by these authors, the energy required for this type of bending appears to be almost independent of sequence, consistent with our conclusion that the kinks observed herein do not appear to have any sequence-specific location. In addition, recent single molecule studies by Bustamante and coworkers (55) have demonstrated clearly that continuum macroscopic elastic theory cannot describe many important elastic properties of DNA.

In conclusion, we have used a novel and advanced AFM technology (MAC mode AFM) to demonstrate by direct imaging a remarkable new sequence-independent kinking phenomenon in DNA that seems to be induced by the presence of Zn²⁺ ions and is observed only in DNA that is axially stressed. Zinc-induced conformational changes in DNA have been postulated to explain the results of more indirect experiments (47, 56) but have not been previously demonstrated by direct imaging to entail stereochemical kinking. We have further explored the ionic strength threshold of this phenomenon and have suggested areas in which it might play a biologically relevant role. The present work demonstrates that Zn²⁺ may play a role in stabilizing kinks that relieve axial strain in DNA under conditions likely to exist in vivo. We have also shown that MAC mode AFM combines a major improvement in image resolution with an ability to image DNA that is relatively gently bound to the substrate. This work suggests how new structures can be probed at relatively high resolution in a variety of ionic environments. Extending these studies to other sequences to determine whether the kinks observed herein are ubiquitous or may be sequence-specific under other conditions would be straightforward. Direct AFM imaging of various protein–nucleic acid complexes (57, 58) has already made major contributions to structural biology and biochemistry and will undoubtedly be facilitated by using MAC mode because of its improved resolution and the capacity for gentle in situ imaging. Other types of measurements are also possible. For example, the accuracy of length measurements permitted by high resolution and the use of circular DNA should enable better discrimination between groove-binding and intercalating DNA ligands.

ABBREVIATIONS

AFM

atomic force microscopy

FWHH

full width at half height

MAC mode

magnetic A/C mode