Abstract
We have used proton magnetic relaxation dispersion (MRD) to study the self-association of bovine β-lactoglobulin variant A (BLG-A) as a function of temperature at pH 4.7 (dimer–octamer equilibrium) and as a function of NaCl concentration at pH 2.5 (monomer–dimer equilibrium). The MRD method identifies coexisting oligomers from their rotational correlation times and determines their relative populations from the associated dispersion amplitudes. From MRD-derived correlation times and hydrodynamic model calculations, we confirm that BLG-A dimers associate to octamers below room temperature. The tendency for BLG-A dimers to assemble into octamers is found to be considerably weaker than in previous light scattering studies in the presence of buffer salt. At pH 2.5, the MRD data are consistent with an essentially complete transition from monomers in the absence of salt to dimers in 1 M NaCl. Because of an interfering relaxation dispersion from nanosecond water exchange, we cannot determine the oligomer populations at intermediate salt concentrations. This nanosecond dispersion may reflect intersite exchange of water molecules trapped inside the large binding cavity of BLG-A.
Keywords: Protein self-association; protein, protein interactions; protein crystallization; bovine β-lactoglobulin; magnetic relaxation dispersion
Bovine β-lactoglobulin (BLG) is the major whey protein in cow’s milk and has served as a model protein for biophysical studies of folding, stability, and self-association (Sawyer and Kontopidis 2000). The dominant genetic variants of BLG, denoted BLG-A and BLG-B, differ in two of the 162 residues. Like other members of the lipocalin family, BLG has a β-barrel fold with a large internal cavity that binds retinol, fatty acids, and other nonpolar molecules (Brownlow et al. 1997; Qin et al. 1998; Uhrínová et al. 2000; Kontopidis et al. 2002). Depending on pH, temperature, and salt concentration, BLG can exist as a monomer, dimer, or octamer (Kumosinski and Timasheff 1966; McKenzie and Sawyer 1967; Sakurai et al. 2001), and it forms amyloid fibrils in the presence of cosolvents such as trifluoroethanol (Gosal et al. 2002) and urea (Hamada and Dobson 2002).
Under physiological conditions (neutral pH and BLG concentration >50 μM), BLG is predominantly dimeric. Although the dimer interface buries only 6% of the monomer surface area, it involves 12 intermolecular hydrogen bonds and 2 ion pairs (Brownlow et al. 1997; Qin et al. 1998), and these specific interactions have been shown to be critical for dimer stability (Kobayashi et al. 2002; Sakurai and Goto 2002). At pH 2 to 3, at which the protein has a net charge of ∼+20, BLG is essentially monomeric under salt-free conditions (Timasheff and Townend 1961b; Baldini et al. 1999; Sakurai et al. 2001). Addition of salt screens the electrostatic repulsion and increases the dimer population.
Below room temperature in the pH range 3.7 to 5.2, BLG reversibly forms a larger oligomer (Townend and Timasheff 1960; Townend et al. 1960; Timasheff and Townend 1961a; Kumosinski and Timasheff 1966; McKenzie et al. 1967; Piazza and Iacopini 2002). This self-association process has a maximum around pH 4.6, just below the isoelectric point, and is more pronounced for BLG-A than for BLG-B, again indicating essential involvement of specific interactions. Static light scattering data indicated that the large oligomer is a cooperatively formed octamer (Townend and Timasheff 1960; Timasheff and Townend 1961a), and the radius of gyration, deduced from small-angle X-ray scattering (SAXS), indicated a compact cubic arrangement of eight monomers (Timasheff and Townend 1964; Witz et al. 1964). A subsequent static light scattering study indicated that intermediate oligomers (tetramers and hexamers) are present in significant amounts at 8°C and 15°C and at BLG concentrations of <1 mM (Kumosinski and Timasheff 1966). From a more recent static and dynamic light scattering study, it was concluded that the effects of oligomerization and other interparticle interactions cannot be separated (Piazza and Iacopini 2002).
The aim of the present work is to shed new light on BLG self-association by using a different experimental technique: magnetic relaxation dispersion (MRD). Within the biomolecular field, MRD has previously been used mostly to study protein hydration and, in particular, internal water molecules in proteins and nucleic acids (Halle et al. 1999; Halle and Denisov 2001). In a recent study of the BPTI decamer, we have demonstrated that water 1H field-cycling MRD can also yield quantitative information about protein self-association in solution (Gottschalk et al. 2003). Under favorable conditions, MRD yields the rotational correlation times and fractional populations of all oligomeric species present in solution. Large oligomers can be detected even at low (<1%) populations, and the method is independent of the association/dissociation kinetics. Because the rotational correlation time is insensitive to long-range interactions, it reflects the true oligomerization state. Moreover, the oligomer species can be identified by comparing the MRD results with hydrodynamically calculated rotational correlation times for detailed oligomer models.
Water 1H and 2H relaxation data from BLG solutions have been reported previously, but only at a single resonance frequency (Kumosinski and Pessen 1982; Pessen et al. 1985; Kumosinski et al. 1991). It is then not possible to separate correlation times and amplitudes for the different oligomeric species. In contrast, our relaxation data span more than four orders of magnitude in frequency. We focus on the temperature-dependent dimer–octamer equilibrium at pH 4.7, but we also report results on the salt-dependent monomer–dimer equilibrium at pH 2.5. We also show that MRD is a sensitive probe of protein purity, revealing a significant population of very large oligomers present even after purification by anion exchange chromatography. Removal of these aggregates by gel filtration is essential in studies of self-association.
Results and Discussion
Temperature-dependent dimer–octamer equilibrium
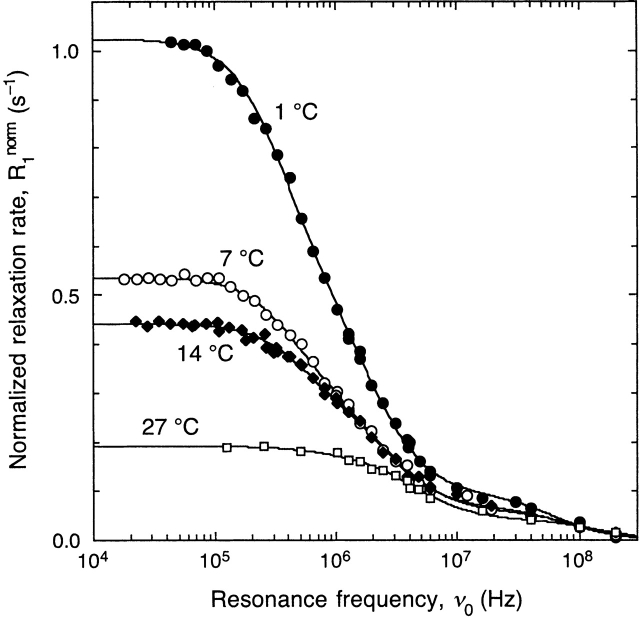
The dimer–octamer equilibrium was studied at pH 4.7 in the absence of buffer or added salt and at BLG concentrations of 0.74 to 0.84 mM. Under these conditions and at 27°C, virtually all BLGs should exist in dimeric form (McKenzie and Sawyer 1967). On lowering the temperature, we observe a strong enhancement of the 1H relaxation rate at low frequencies and a low-frequency shift of the dispersion region (Fig. 1 ▶). These changes indicate increased correlation times. According to the Stokes-Einstein-Debye relation, the rotational correlation time (τ R) is proportional to η(T) / T, where η is the temperature-dependent viscosity of the aqueous solvent. If the size and shape of the protein does not change with temperature, we may write τR(T) = γ τ R(T0), with a dynamic scaling factor γ = T0 η(T) / (T η[T0]). Taking T0 = 300 K as the reference temperature, we have γ = 2.226 at 274 K. However, the low-frequency 1H relaxation rate R1 increases by more than a factor five on going from 300 to 274 K (Fig. 1 ▶). We can thus conclude that the protein structure, or oligomerization state, depends strongly on temperature.
Figure 1.
1H relaxation dispersion profiles from aqueous BLG solutions at pH 4.7 (no buffer and no added salt) and temperatures from 1°C to 27°C. The data have been normalized to 1.00 mM BLG. The dispersion curves resulted from a joint fit according to equations 1 and 2 with N = 2. The three correlation times were constrained to scale with temperature as η(T) / T.
All the dispersion profiles in Figure 1 ▶ exhibit a small-amplitude dispersion step at frequencies ∼108 Hz. This frequency corresponds to a correlation time of ∼1 nsec, an order of magnitude shorter than the rotational correlation of the BLG dimer (or monomer). This dispersion step must therefore be attributed to water molecules with residence times of ∼1 nsec (see below). The main dispersion step, which reflects the rotational diffusion of BLG oligomers, is broadened at low temperatures and cannot be reproduced with a single rotational correlation time. This qualitative observation indicates that more than one oligomer species is present at low temperatures.
To determine the size and relative population of the oligomers, we fitted the theoretical relaxation dispersion expression (equations 1, 2) to the relaxation data in Figure 1 ▶. Three correlation times are needed to reproduce the data to within the experimental accuracy (as judged by the F test): a water residence time τ0 and two rotational correlation times, τ1 and τ2. If the temperature variation alters the oligomer populations without changing the oligomer structures, it should be possible to fit all four dispersion profiles jointly to three correlation time parameters, which we choose as τ0, τ1, and τ2 at 300 K. The correlation times at the other temperatures are then obtained from the relation τR(T) = γ τR(T0) with known scaling factors γ (Table 1). The excellent fit (χ2 = 1.8) in Figure 1 ▶ supports this reasonable assumption.
Table 1.
Results of joint fit to four 1H MRD profiles at pH 4.7
| T (°C) | CPa (mM) | γb | Bc,d (107 sec−2) | xoctamerd | ΔG°octamerd (kJ/mole) |
| 1.0 | 0.84 | 2.226 | 1.28 (3) | 0.20 (4) | −48 (1) |
| 7.0 | 0.82 | 1.797 | 0.73 (3) | 0.18 (4) | −49 (1) |
| 14.0 | 0.82 | 1.435 | 0.80 (4) | 0.16 (4) | −50 (1) |
| 27.0 | 0.74 | 1 | 0.68 (5) | 0.03 (2) | −48 (1) |
a Total BLG concentration.
b Dynamic scaling factor. γ = 300 η(T)/[T η(300 K)].
c Total fluctuation amplitude, B = b1 + b2, normalized to CP = 1.00 mM.
d Uncertainty in last position given within parentheses.
The correlation times deduced from the fit are τ0 = 0.65 ± 0.11 nsec, τ1 = 20.4 ± 0.9 nsec, and τ2 = 111 ± 3 nsec, all at 300 K. The rotational correlation time of the BLG-A monomer has been determined to 7.30 ± 0.05 nsec from 15N relaxation at pH 2.6 (50 mM phosphate buffer), 310 K, and 1 mM BLG concentration (Uhrínová et al. 2000). Scaling this to 300 K, we obtain τR(monomer) = 9.09 ± 0.06 nsec. Hydrodynamic calculations, based on the crystal structure of the BLG-A monomer and dimer (Qin et al. 1998), yield τR(dimer) / τR(monomer) = 2.26 (see Materials and Methods). We thus obtain τR(dimer) = 20.5 ± 0.1 nsec. The close agreement with the correlation time τ1 derived from the relaxation dispersions in Figure 1 ▶ leads us to identify this component with the BLG dimer. There is also good agreement with dimer rotational correlation times determined by fluorescence depolarization (quoted values have been scaled to 300 K): 19.4 nsec for BLG-A at pH 5.5 (Wahl and Timasheff 1969) and 17.9 nsec for BLG-B at pH 7.8 (Collini et al. 2002). The slightly shorter values obtained with this method might be due to internal motion of the fluorescence label.
The detailed structure of the BLG octamer is not known, but it appears to be very compact. SAXS yields a radius of gyration, RG = 21.6 ± 0.4 Å, for the BLG-A dimer at pH 5.7 (100 mM acetate buffer) and room temperature (Witz et al. 1964). This agrees perfectly with the value, RG = 21.6 Å, that we have calculated from the crystal structure of the BLG-A dimer (Protein Data Bank [PDB] code 1BSY with hydrogen atoms added). For the octamer, studied at pH 4.5 (100 mM acetate buffer) and 3°C, the SAXS study yielded RG = 34.4 ± 0.4 Å (Witz et al. 1964). This was shown to be consistent with a cubic array of eight spheres (Timasheff and Townend 1964; Witz et al. 1964). For such an array, hydrodynamic calculations yield τR(octamer) / τR(monomer) = 1/0.075 (García de la Torre and Bloomfield 1981). Combining this with the experimentally derived τR(monomer) value quoted above, we obtain τR(octamer) = 121 nsec at 300K. This is only 10% from the MRD-derived correlation time τ2 and, given that the hydrodynamic model lacks atomic detail, strongly indicates that the low-frequency component of the dispersion profile is produced by a BLG octamer with the cubic structure deduced from SAXS data.
Fluorescence depolarization on 1.1 mM BLG-A at pH 4.6 (100 mM acetate buffer) and 2°C yielded a rotational correlation time of 65 nsec after scaling to 300 K (Wahl and Timasheff 1969). This much smaller value was deduced under the assumption that the BLG solution was monodisperse. However, a substantial dimer population should be present under these conditions (see below). The correlation time deduced from fluorescence depolarization should therefore be an effective one, reflecting both dimers and octamers. In contrast, MRD data allow the rotational diffusion of dimer and octamer to be resolved. It should be noted that even if a substantial dimer population were present in the SAXS study discussed above, the observed radius of gyration would not deviate much from that of the more massive octamer.
Having identified the oligomeric species as dimer and octamer, we can now determine their relative populations from the mean-square fluctuation amplitudes b1 and b2 derived from the fit (see equation 1). These amplitudes can be expressed as bn = xn βn , where xn is the fraction of BLG molecules that belong to the nth oligomer species or, equivalently, the weight fraction of that species (Gottschalk et al. 2003). The intrinsic mean-square fluctuation amplitude βn is proportional to the number of protons (per BLG monomer) with residence times long enough (>τR,n) to sample the rotational diffusion of the oligomer but short enough (<1/[βn τR,n]) to act as a relaxation sink for the observed water 1H magnetization (Halle et al. 1999; Halle and Denisov 2001). We assume that the number of internal water molecules and rapidly exchanging labile hydrogens are the same (on a monomer basis) in the dimer and the octamer. At each temperature, we then have β1 = β2, and it follows that the fractional populations can be obtained as xn = bn / B, where B = b1 + b2. If this assumption is correct, B should be independent of the oligomer fractions, but it may depend on temperature. As seen from Table 1, B is nearly constant at the three higher temperatures but is substantially larger at 274 K. This might reflect a low-temperature structural change in BLG that traps additional hydration water molecules. In this connection, it is interesting to note that monomeric BLG-A at pH 2.0 to 2.5 has been shown to undergo cold-denaturation in the presence of urea (Griko and Privalov 1992; Griko and Kutyshenko 1994; Katou et al. 2001).
The analysis of our MRD data shows that the octamer fraction increases from 0.03 at 300 K to 0.20 at 274 K (Table 1). From the octamer fraction xoctamer ≡ x2, we may calculate a stoichiometric association constant for an octamer formed with full cooperativity as Koctamer = 2xoctamer / ([1 − xoctamer]4C3P), where CP is the total BLG concentration on a monomer basis. The associated standard free energy of association, calculated as ΔG°octamer = −RT lnKoctamer, is remarkably constant at −49 ± 1 kJ mole−1 over the investigated temperature range (Table 1). Static light scattering studies of BLG-A at pH 4.65 (100 mM acetate buffer) yielded ΔG°octamer = −48.9 kJ mole at 298 K (Kumosinski and Timasheff 1966), in good agreement with our result. However, these investigators found that ΔG°octamer varies linearly with temperature, reaching −64.4 kJ mole−1 at 274 K. This would correspond to an octamer fraction of 0.80 in our 274 K sample, four times higher than we obtained. Such a high octamer fraction is definitely ruled out by our data. Our result at 274 K, xoctamer = 0.20 ± 0.04, is quite robust and remains within the given uncertainty whether the dispersion is fitted separately or jointly with the other dispersions and whether the correlation times are freely adjusted or frozen to independently established values (see above).
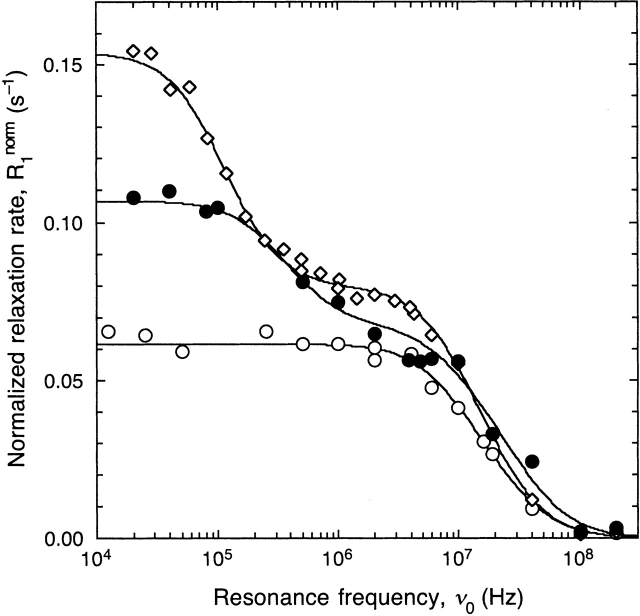
We can think of several possible reasons for the discrepancy between the low-temperature octamer fraction derived from the present MRD data and that deduced from static light scattering data (Kumosinski and Timasheff 1966). First, the light scattering study was performed in the presence of 100 mM acetate buffer, whereas our samples are free from added salt (apart from that introduced by pH adjustment, estimated to be <2 mM). Although the protein is near its isoelectric pH, salt screening of electrostatic repulsion should enhance octamer formation. We note also that light scattering data may be significantly affected by interparticle interactions (Piazza and Iacopini 2002) and/or trace amounts of larger aggregates. Our BLG preparation was purified by anion exchange chromatography as well as gel filtration. As discussed in Materials and Methods, the gel filtration step is necessary to remove a high-molecular-weight species present in BLG from both investigated sources. Trace amounts of such a high-molecular-weight impurity are readily detected by MRD (see Fig. 3 ▶).
Figure 3.
1H relaxation dispersion profiles from aqueous 1 mM BLG solutions at 27°C and pH 2.5. The protein source and purification level for the three profiles are as follows: (1) Sigma, anion exchange chromatography (diamonds); (2) INRA, anion exchange chromatography (filled circles); and (3) INRA, anion exchange chromatography followed by gel filtration (open circles). Dispersion steps <1 MHz in cases 1 and 2 are due to 1.0 ± 0.5% of high-molecular-weight impurity with correlation time 0.25 ± 0.06 μsec (INRA) and 0.82 ± 0.05 μsec (Sigma) as deduced from the depicted tri-Lorentzian fits with the intermediate correlation time frozen to 9.1 nsec (as expected for the monomer). The solvent of sample 2 contained 25 vol% D2O.
Whereas earlier studies concluded that the BLG octamer forms by cooperative association of four dimers (Townend and Timasheff 1960; Timasheff and Townend 1961a), a subsequent study noted that the concentration dependence of the static light scattering could not be quantitatively reproduced without invoking intermediate oligomers (Kumosinski and Timasheff 1966). Thus, at pH 4.65, 281 K, and 1 mM total BLG-A, ∼25% of the BLG was predicted to exist as tetramers or hexamers (Kumosinski and Timasheff 1966). Although intermediates cannot be categorically ruled out by our MRD data, the excellent fit with only two rotational correlation times indicates that any intermediates are present at low concentrations.
Salt-dependent monomer–dimer equilibrium
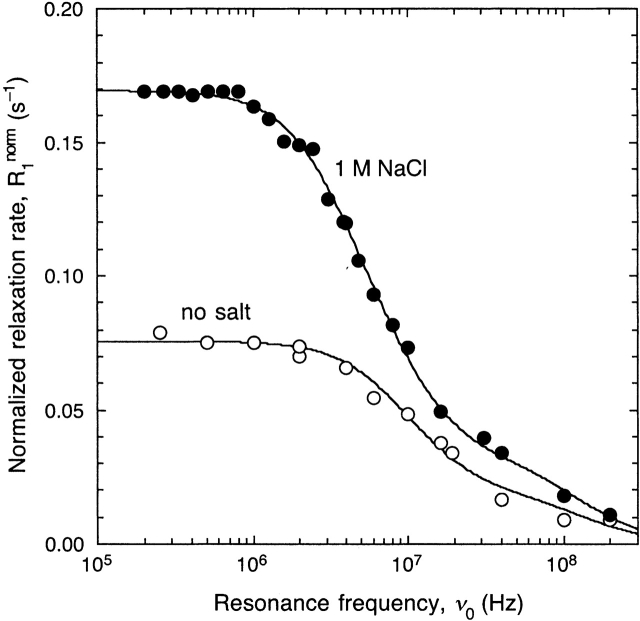
The monomer–dimer equilibrium was studied at pH 2.5 and 300 K in the presence of 0, 0.010, 0.050, or 1.00 M added NaCl. We note that the "no salt" sample has an ionic strength of 15 to 20 mM due to the chloride ions added with the HCl used to adjust the pH. The BLG concentration was 0.71 to 1.00 mM. With increasing salt concentration, we observed a monotonic increase of the dispersion amplitude and a low-frequency shift of the dispersion, indicating salt-induced formation of larger, more slowly tumbling oligomers. This is shown in Figure 2 ▶ for the two extreme cases. The salt effect at pH 2.5 is much smaller than the effect of temperature at pH 4.7 (note the different R1 scales in Figs. 1 and 2 ▶ ▶). As a result, the high-frequency dispersion step from water molecules with nanosecond correlation times now makes a larger relative contribution to the dispersion profile. Moreover, the rotational correlation times of the BLG-A monomer and dimer only differ by a factor of 2.26 (see Materials and Methods), making it difficult to resolve the individual Lorentzian contributions to the dispersion.
Figure 2.
1H relaxation dispersion profiles from aqueous BLG solutions at pH 2.5 (no buffer) and 27°C without added salt and in the presence of 1 M NaCl. The data have been normalized to 1.00 mM BLG. The dispersion curves resulted from a joint fit according to equations 1 and 2 with N = 2 and frozen correlation times (see text).
In an attempt to overcome these problems, we fitted the no salt and 1 M NaCl dispersions with the three correlation times fixed. The water correlation time τ0 was taken as 0.65 nsec, as obtained (at 300 K) from the fit to the pH 4.7 MRD data, in which this dispersion step is better resolved due to absence of BLG monomers. The monomer correlation time τ1 was set to 9.1 nsec, as determined by 15N relaxation (Uhrínová et al. 2000), and the dimer correlation time τ2 was set to 20.4 nsec, as obtained (at 300 K) from the pH 4.7 MRD data and also from hydrodynamic calculations (see above). For the 1 M NaCl solution, these correlation times were multiplied by a factor 1.095, accounting for the higher bulk solvent viscosity. As seen from Figure 2 ▶, the dispersion profiles are well described by these correlation times.
As for the pH 4.6 MRD data, we can determine the dimer fraction xdimer = x2 from the mean-square fluctuation amplitudes bn = xn βn assuming that β1 = β2. As required if this assumption is correct, B = b1 + b2 does not vary significantly with salt concentration: B = (0.65 ± 0.06) × 107 sec−2 in the absence of salt and (0.7 ± 0.1) × 107 sec−2 in 1 M NaCl. This analysis yields xdimer = 0 in the absence of salt (this dispersion profile is thus modeled with only two Lorentzians) and xdimer = 0.4 ± 0.1 in 1 M NaCl. Previous studies of the monomer–dimer equilibrium of BLG-A at pH 2.3 to 3.0 by sedimentation, light scattering, and SAXS indicate that at pH 2.5, 300 K, and 1 mM BLG, xdimer ≈ 0.1 in the absence of added salt and xdimer ≈ 0.9 in 1 M NaCl (Timasheff and Townend 1961b; Tang and Adams 1973; Baldini et al. 1999; Sakurai et al. 2001). Whereas our results agree with previous work in the absence of salt, there is a substantial discrepancy at 1 M NaCl. This can be resolved as follows.
A statistical analysis (using the F test) shows that the 1 M NaCl data are reproduced within experimental accuracy by two Lorentzians. Without fixing correlation times, these data therefore cannot be used to establish coexisting monomer and dimer populations. The dimer fraction derived from the tri-Lorentzian fit in Figure 2 ▶ depends on the values assigned to the fixed correlation times. Whereas the monomer and dimer rotational correlation times τ1 and τ2 are accurately known, the value of the water-exchange correlation time τ0 is less certain. To test if our data are consistent with previous results for the dimer fraction, we thus performed bi-Lorentzian fits with τ0 freely adjustable but τ1 (no salt) and τ2 (1 M NaCl) fixed as before. The resulting fits are virtually indistinguishable from those shown in Figure 2 ▶, but now τ0 ≈ 3 nsec. Considering that the net charge of BLG is much higher at pH 2.5 (+20) than at pH 4.7 (+4), such a pH dependence in τ0 cannot be ruled out. We therefore conclude that the present MRD data are consistent with previous results (Timasheff and Townend 1961b; Tang and Adams 1973; Baldini et al. 1999; Sakurai et al. 2001), indicating that under our conditions, BLG is almost completely monomeric in the absence of salt and almost completely dimeric in 1 M NaCl.
Finally, we note that the 1 M NaCl dispersion shows a small low-frequency step (below the frequency range of Fig. 2 ▶) corresponding to a correlation time of 1.0 ± 0.3 μsec. This indicates that small amounts of very large BLG aggregates form at high salt concentration, despite the high structural charge of BLG at pH 2.5.
Conclusions
The self-association of bovine BLG has been extensively studied by several physical techniques in the past. Whereas the salt-dependent monomer–dimer equilibrium at pH 2 to 3 has been characterized in considerable detail, the temperature-dependent dimer–octamer equilibrium near the isoelectric point is not as well understood. In particular, a high-resolution structure of the octamer is not available.
Here, we have used proton MRD to shed further light on the dimer–octamer equilibrium of BLG-A at pH 4.7. The MRD data reveal two oligomeric species with rotational correlation times of 20.4 ± 0.8 nsec and 111 ± 3 nsec at 27°C. The shorter correlation time agrees with the dimer correlation time, 20.5 ± 0.1 nsec, predicted on the basis of the monomer correlation time determined by 15N spin relaxation (Uhrínová et al. 2000) and our hydrodynamic calculations on the monomer and dimer crystal structures. The longer correlation time is consistent with a crude theoretical estimate, 121 nsec, based on the cubic arrangement of eight monomers predicted from SAXS data (Timasheff and Townend 1964; Witz et al. 1964).
Whereas the MRD data confirm that BLG-A self-associates to dimers and octamers at pH 4.7, they differ from previously reported light scattering results with regard to the relative populations of these oligomeric species. Reasonable agreement is found at 27°C, but we obtain a significantly lower octamer fraction at 1°C. This difference may be caused by the presence of buffer salt in all previous studies, which should promote octamer formation by electrostatic screening.
We have also used MRD to study the monomer–dimer equilibrium at pH 2.5 as a function of NaCl concentration. The MRD data are consistent with an essentially monomeric protein in the absence of salt and an essentially dimeric protein in 1 M NaCl, with the expected rotational correlation times for the monomer and dimer. However, because of the presence of an additional dispersion step from water molecules with nanosecond correlation time, it is not possible to resolve the monomer and dimer contributions in a unique way. Because this nanosecond correlation time is shorter than the rotational correlation time of the BLG monomer, it must reflect water motions. Water correlation times in this range have previously been associated with the exchange of water molecules from singly occupied deep surface pockets in several proteins (Halle 1999) and with intersite exchange among the ∼20 water molecules trapped inside the internal cavity of a fatty acid binding protein (Wiesner et al. 1999). Few, if any, water molecules have been crystallographically localized within the internal binding cavity of BLG. However, positional disorder could make such water molecules difficult to observe at the resolution of the current BLG structures (Brownlow et al. 1997; Qin et al. 1998; Kontopidis et al. 2002). Further MRD work, with more extensive data at high frequencies, would be required to obtain reliable information about the number of water molecules responsible for the nanosecond dispersion. Difference-MRD experiments with a bound ligand, such as retinol, should also be useful in this regard.
Materials and methods
Protein purification
BLG-A, prepared from the milk of homozygous cows at the INRA Laboratoire de Recherche de Technologie Laitiére, was generously supplied by Dr. C. Holt of the Hannah Research Institute (Ayr, Scotland). A second batch of BLG-A was purchased from Sigma (L-7880, lot no. 70K7049). Both protein preparations were first purified by anion exchange chromatography at pH 6.0 (10 mM MES buffer) on a DEAE-sephacel column, eluted with a 25 to 300 mM NaCl gradient. Although the purified protein preparations yielded a single band in agarose gel electrophoresis and SDS-PAGE, ∼1% of high-molecular-weight species (probably a BLG polymer) was detected in both preparations by MRD at pH 2.5 (Fig. 3 ▶). To remove this impurity, we further purified the INRA preparation by gel filtration at pH 2.7 (10 mM citric acid, 50 mM NaCl) on a Sephadex G-50 column. The protein was then dialyzed against milli-Q water and lyophilized. All MRD data reported here (except profiles 1 and 2 in Fig. 3 ▶) were measured on samples made from this preparation.
Preparation of MRD samples
MRD samples were made by dissolving the purified protein in oxygen depleted water (<0.001% O2, Fluka BioChemika). The pH value, which was 4.6 to 4.7 after dissolution, was adjusted by microliter additions of HCl. No buffers were used. All quoted pH values were measured at room temperature. For the salt series, desiccator dried NaCl (>99.5%, Merck) was added, whereupon the solution was centrifuged at 14,000g for 3 min to remove a small fraction of aggregated material. Protein concentrations were determined spectrophotometrically (Shimadzu UV-1601) at 278 nm by using an extinction coefficient of 1.11 mL mg−1 cm−1, determined from quantitative amino acid analysis on two samples. To remove paramagnetic oxygen, the solution was gently bubbled with argon gas during 4 h, whereupon the 10-mm NMR tube was sealed with a septum. With this procedure, the 1H relaxation rate in a pure water sample was found to be 0.267 ± 0.008 sec−1, in agreement with the standard literature value of 0.266 sec−1 (Hindman et al. 1973), and remained within 1% of this value for at least 10 d.
Relaxation dispersion measurements
The longitudinal relaxation of the water 1H resonance was studied from 10 kHz to 200 MHz by using (1) a Stelar Spinmaster fast field-cycling (FC) spectrometer (20 kHz to 6 MHz), (2) a field-variable iron-core magnet (Drusch) equipped with a Tecmag Discovery console (10 to 78 MHz), and (3) Bruker Avance DMX 100 and 200 spectrometers with conventional cryomagnets (100.1 and 200.1 MHz). The temperature was maintained to within ±0.1°C using a Stelar variable temperature control unit (< 100 MHz) or a Bruker Eurotherm regulator (at 100 and 200 MHz). Temperatures were checked by using a thermocouple referenced to an ice-water bath.
The longitudinal relaxation rate R1 was measured with the inversion recovery method (fixed-field experiments) and by the prepolarized (<4 MHz) or nonpolarized (>4 MHz, avoiding short evolution times) FC protocols. The small contribution from nonexchanging protein protons was eliminated by selective integration (fixed field) or by delayed acquisition (FC). All other details of the relaxation experiments were as previously described (Gottschalk et al. 2003). The accuracy in R1 is estimated to ±1% at the two highest fields and 1% to 2% (1 SD) at the other fields.
Analysis of relaxation dispersion data
The measured 1H relaxation rate is due to thermal fluctuations of intramolecular and intermolecular magnetic dipole–dipole couplings experienced by water protons and labile BLG protons in fast or intermediate exchange (residence time <10 msec, typically) with the water protons (Halle et al. 1999; Halle and Denisov 2001). The relaxation dispersion, that is, the frequency dependence of R1, is produced by long-lived (residence time 10−9 to 10−2 sec) water molecules in intimate association with the protein and by labile protons with residence times in the same range. The dispersion profile, R1(ω0), from a solution containing BLG in N different oligomeric states is described by the following relations (Halle et al. 1999; Halle and Denisov 2001)
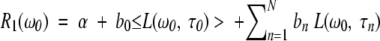 |
(1) |
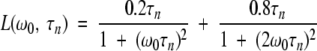 |
(2) |
Here, bn and τn are the mean-square fluctuation amplitude and correlation time, respectively, associated with the nth dispersion step. The correlation time τn is related to the BLG oligomer rotational correlation time τR,n and the mean proton residence time τH,n as (Halle et al. 1999)
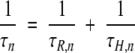 |
(3) |
Labile protons generally have residence times much longer than the protein rotational correlation time and therefore do not contribute to τn. This is usually the case also for protons in deeply buried internal water molecules. However, water molecules in deep surface pockets or trapped in large internal cavities may have site residence times in the range of 1 to 10 nsec (Halle 1999; Wiesner et al. 1999) and will then shorten the correlation time τn according to equation 3. All our MRD profiles from BLG solutions show a dispersion step with a correlation time of ∼1 nsec, attributable to such water molecules. This contribution is modeled by the second term in equation 1, which, for simplicity, is represented by a single correlation time. Our main focus here is on the dispersion steps n = 1, 2,…, N that report on the oligomeric species of BLG (monomer, dimer, or octamer). The correlation time τn can be identified with the isotropic rotational correlation time τR of the nth oligomer species, and the amplitude bn allows its fractional population to be determined.
For brevity, the functions L(ω0, τn) will be referred to as Lorentzians, even though they contain two Lorentzian components. In the analysis of MRD data, we actually used a more involved dispersion function, which is a linear combination of the intramolecular dispersion function in equation 2 and an intermolecular dispersion function (Abragam 1961; Halle et al. 1999). The relative weight of the intermolecular function was set to 0.33 (Venu et al. 1997), but any value in the allowed range of 0 to 1 could be used without significantly affecting the correlation times and amplitudes deduced from the fits. The parameter α in equation 1 represents all frequency-independent contributions to the measured relaxation rate, including bulk water, rapidly exchanging (τH << 1 nsec) surface waters, and the secular (zero-frequency) intermolecular contribution from internal waters and labile BLG protons (Venu et al. 1997). Because of incomplete characterization of the highest-frequency dispersion step (with a correlation time of ∼1 nsec), the α parameter could not be determined with useful accuracy. The dispersion profiles are therefore displayed with the small frequency-independent contribution subtracted and with the frequency-dependent part normalized to the same BLG concentration (Gottschalk et al. 2003):
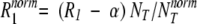 |
(4) |
where NT is the number of water molecules per BLG monomer in the solution and NTnorm was taken as 55,000, corresponding to a BLG monomer concentration of 1.00 mM.
The experimental relaxation dispersion data were subjected to nonlinear Marquardt-Levenberg χ2 minimization (Press et al. 1992) with the model function given by equations 1 and 2. This fit involves the 2N + 1 parameters α, bn, and τn, with the products bnτn constrained to be nonnegative. The number N of Lorentzians to be included in the fit was determined objectively by the F test with a cutoff probability of 0.9 (Press et al. 1992; Halle et al. 1998). The dispersions were thus found to be adequately modeled by two Lorentzians (N = 2) in addition to the nanosecond water dispersion (n = 0). For each of the two sets of experiments (salt dependence and temperature dependence), the dispersion profiles were fitted jointly under the assumption that the same oligomers are present under all conditions but with different relative populations. Quoted uncertainties in the fitted parameter values correspond to 1 SD and were obtained by the Monte Carlo method (Press et al. 1992) using 1000 synthetic data sets.
Hydrodynamic calculations of rotational correlation times
The rotational correlation times τ1 and τ2 obtained from the MRD data contain information about oligomer size and shape. To verify our assignments of oligomer species, we carried out hydrodynamic calculations of the rotational diffusion tensor DR of BLG-A with the program HYDROPRO, version 5.a (García de la Torre et al. 2000). In these calculations, each nonhydrogen atom in a crystallographic model of the protein is replaced by a spherical bead of radius aH. The shell of beads remaining after all internal beads have been deleted is then filled with smaller spheres of radius σ that act as point sources of hydrodynamic friction. The rotational diffusion tensor DR is computed as a function of σ and extrapolated to σ = 0 (García de la Torre and Bloomfield 1981). The rank-2 isotropic rotational correlation time is defined as τR = (2 Tr DR)−1. Because macroscopic continuum hydrodynamics is not strictly valid on the atomic scale, this calculation does not necessarily yield results in quantitative agreement with experiment. The approach usually adopted is to regard the bead radius aH as an empirical parameter (rather than using the van der Waals radii of the actual atoms), the value of which is determined by requiring that the calculation agrees with the experimental value of a particular hydrodynamic quantity, such as τR (García de la Torre et al. 2000).
Our calculations are based on the crystal structure 1BSY of BLG-A at 298 K (pH 7.1) determined at 2.24 Å resolution in the trigonal space group P 3221 with six asymmetric units per unit cell (Qin et al. 1998). For calculations on the monomer, we used the atomic coordinates deposited in the PDB file (which includes all 162 residues). For the dimer, we generated the other subunit by the crystallographic symmetry operations given in the PDB file (molecule 6). For monomeric BLG-A, we calculated τR at 27°C for aH values in the range of 1.0 to 4.0 Å. Interpolation at the experimental value τR = 9.09 ± 0.06 nsec (Uhrínová et al. 2000) yields aH = 2.97 ± 0.04 Å. We then used this bead radius to calculate the ratio of the rotational correlation times for the BLG-A dimer and monomer, obtaining τR(dimer) / τR(monomer) = 2.26. This ratio is quite insensitive to the bead radius, varying by only 0.15 over the range aH = 1.0 to 4.0 Å.
For a general asymmetric top, the dispersion function (or spectral density) involves five rotational correlation times. The BLG-A monomer, however, is very nearly spherical, and the ratio of the longest and shortest rotational correlation times is 1.08. The dimer is better described as a prolate symmetric top, but the correlation time ratio of 1.45 is not large enough to produce a significant deviation from spherical top behavior in the MRD profile. Accordingly, we describe both monomer and dimer with single (isotropic) rotational correlation times.
Acknowledgments
We thank Hans Lilja and Vladimir Denisov for spectrometer assistance and Peter Sellers for helpful suggestions. This work was supported by the Swedish Research Council and the Crafoord Foundation.
The publication costs of this article were defrayed in part by payment of page charges. This article must therefore be hereby marked "advertisement" in accordance with 18 USC section 1734 solely to indicate this fact.
Article and publication are at http://www.proteinscience.org/cgi/doi/10.1110/ps.0305903.
References
- Abragam, A. 1961. The principles of nuclear magnetism. Clarendon Press, Oxford.
- Baldini, G., Beretta, S., Chirico, G., Franz, H., Maccioni, E., Mariani, P., and Spinozzi, F. 1999. Salt-induced association of β-lactoglobulin by light and X-ray scattering. Macromolecules 32 6128–6138. [Google Scholar]
- Brownlow, S., Morais Cabral, J.H., Cooper, R., Flower, D.R., Yewdall, S.J., Polikarpov, I., North, A.C.T., and Sawyer, L. 1997. Bovine β-lactoglobulin at 1.8 Å resolution: Still an enigmatic lipocalin. Structure 5 481–495. [DOI] [PubMed] [Google Scholar]
- Collini, M., Leo, B., Baldini, G., Monaco, H.L., and Galliano, M. 2002. Probing protein aggregation by time-resolved fluorescence during β-lactoglobulin crystal growth. Eur. Biophys. J. 31 111–117. [DOI] [PubMed] [Google Scholar]
- García de la Torre, J. and Bloomfield, V.A. 1981. Hydrodynamic properties of complex, rigid, biological macromolecules: Theory and applications. Q. Rev. Biophys. 14 81–139. [DOI] [PubMed] [Google Scholar]
- García de la Torre, J., Huertas, M.L., and Carrasco, B. 2000. Calculation of hydrodynamic properties of globular proteins from their atomic-level structure. Biophys. J. 78 719–730. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gosal, W.S., Clark, A.H., Pudney, P.D.A., and Ross-Murphy, S.B. 2002. Novel amyloid fibrillar networks derived from a globular protein: β-Lactoglobulin. Langmuir 18 7174–7181. [Google Scholar]
- Gottschalk, M., Venu, K., and Halle, B. 2003. Protein self-association in solution: The bovine pancreatic trypsin inhibitor decamer. Biophys. J. 84 3941–3958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griko, Y.V. and Kutyshenko, V.P. 1994. Differences in the processes of β-lactoglobulin cold and heat denaturations. Biophys. J. 67 356–363. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Griko, Y.V. and Privalov, P.L. 1992. Calorimeteric study of the heat and cold denaturation of β-lactoglobulin. Biochemistry 31 8810–8815. [DOI] [PubMed] [Google Scholar]
- Halle, B. 1999. Water in biological systems. In Hydration processes in biology (ed. M.-C. Bellisent-Funel), pp. 233–249. IOS Press, Amsterdam.
- Halle, B., and Denisov, V.P. 2001. Magnetic relaxation dispersion studies of biomolecular solutions. Meth. Enzymol. 338 178–201. [DOI] [PubMed] [Google Scholar]
- Halle, B., Jóhannesson, H., and Venu, K. 1998. Model-free analysis of stretched relaxation dispersions. J. Magn. Reson. 135 1–13. [DOI] [PubMed] [Google Scholar]
- Halle, B., Denisov, V.P., and Venu, K. 1999. Multinuclear relaxation dispersion studies of protein hydration. In Biological magnetic resonance (eds. N.R. Krishna and L.J. Berliner), pp. 419–484. Kluwer Academic/Plenum, New York.
- Hamada, D. and Dobson, C.M. 2002. A kinetic study of β-lactoglobulin amyloid fibril formation promoted by urea. Protein Sci. 11 2417–2426. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hindman, J.C., Svirmickas, A., and Wood, M. 1973. Relaxation processes in water: A study of the proton spin-lattice relaxation time. J. Chem. Phys. 59 1517–1522. [Google Scholar]
- Katou, H., Hoshino, M., Kamikubo, H., Batt, C.A., and Goto, Y. 2001. Native-like β-hairpin retained in the cold-denatured state of bovine β-lactoglobulin. J. Mol. Biol. 310 471–484. [DOI] [PubMed] [Google Scholar]
- Kobayashi, T., Ikeguchi, M., and Sugai, S. 2002. Construction and characterization of β-lactoglobulin chimeras. Proteins 49 297–301. [DOI] [PubMed] [Google Scholar]
- Kontopidis, G., Holt, C., and Sawyer, L. 2002. The ligand-binding site of bovine β-lactoglobulin: Evidence for a function? J. Mol. Biol. 318 1043–1055. [DOI] [PubMed] [Google Scholar]
- Kumosinski, T.F. and Pessen, H. 1982. A deuteron and proton magnetic resonance relaxation study of β-lactoglobulin A association: Some approaches to the Scatchard hydration of globular proteins. Arch. Biochem. Biophys. 218 286–302. [DOI] [PubMed] [Google Scholar]
- Kumosinski, T.F. and Timasheff, S.N. 1966. Molecular interactions in β-lactoglobulin, X: The stoichiometry of the β-lactoglobulin mixed tetramerization. J. Am. Chem. Soc. 88 5635–5642. [DOI] [PubMed] [Google Scholar]
- Kumosinski, T.F., Pessen, H., and Farrell, H.M. 1991. Protein-water interactions from 2H NMR relaxation studies: Influence of hydrophilic, hydrophobic, and electrostatic interactions. In Water relationships in food (eds. H. Levine and L. Slade), pp. 541–560. Plenum Press, New York. [DOI] [PubMed]
- McKenzie, H.A. and Sawyer, W.H. 1967. Effects of pH on β-lactoglobulin. Nature 214 1101–1104. [DOI] [PubMed] [Google Scholar]
- McKenzie, H.A., Sawyer, W.H., and Smith, M.B. 1967. Optical rotatory dispersion and sedimentation in the study of association-dissociation: Bovine β-lactoglobulins near pH 5. Biochim. Biophys. Acta 147 73–92. [DOI] [PubMed] [Google Scholar]
- Pessen, H., Purcell, J.M., and Farrell, H.M. 1985. Proton relaxation rates of water in dilute solutions of β-lactoglobulin: Determination of cross relaxation and correlation with structural changes by the use of two genetic variants of a self-associating globular protein. Biochim. Biophys. Acta 828 1–12. [Google Scholar]
- Piazza, R. and Iacopini, S. 2002. Transient clustering in a protein solution. Eur. Phys. J. 7 45–48. [Google Scholar]
- Press, W.H., Teukolsky, S.A., Vetterling, W.T., and Flannery, B.P. 1992. Numerical recipes in C, 2nd ed. Cambridge University Press, Cambridge, UK.
- Qin, B.Y., Bewley, M.C., Creamer, L.K., Baker, H.M., Baker, E.N., and Jameson, G.B. 1998. Structural basis of the Tanford transition in bovine β-lactoglobulin. Biochemistry 37 14014–14023. [DOI] [PubMed] [Google Scholar]
- Sakurai, K. and Goto, Y. 2002. Manipulating monomer–dimer equilibrium of bovine β-lactoglobulin by amino acid substitution. J. Biol. Chem. 277 25735–25740. [DOI] [PubMed] [Google Scholar]
- Sakurai, K., Oobatake, M., and Goto, Y. 2001. Salt-dependent monomer–dimer equilibrium of bovine β-lactoglobulin at pH 3. Protein Sci. 10 2325–2335. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sawyer, L. and Kontopidis, G. 2000. The core lipocalin, bovine β-lactoglobulin. Biochim. Biophys. Acta 1482 136–148. [DOI] [PubMed] [Google Scholar]
- Tang, L.-H. and Adams, E.T. 1973. Sedimentation equilibrium in reacting systems, VII: The temperature-dependent self-association of β-lactoglobulin A at pH 2.46. Arch. Biochem. Biophys. 157 520–530. [DOI] [PubMed] [Google Scholar]
- Timasheff, S.N. and Townend, R. 1961a. Molecular interactions in β-lactoglobulin, V: The association of the genetic species of β-lactoglobulin below the isoelectric point. J. Am. Chem. Soc. 83 464–469. [Google Scholar]
- ———. 1961b. Molecular interactions in β-lactoglobulin, VI: The dissociation of the genetic species of β-lactoglobulin at acid pH’s. J. Am. Chem. Soc. 83 470–473. [Google Scholar]
- ———. 1964. Structure of the β-lactoglobulin tetramer. Nature 203 517–519. [Google Scholar]
- Townend, R. and Timasheff, S.N. 1960. Molecular interactions in β-lactoglobulin, III: Light scattering investigation of the stoichiometry of the association between 3.7 and 5.2. J. Am. Chem. Soc. 82 3168–3174. [Google Scholar]
- Townend, R., Winterbottom, R.J., and Timasheff, S.N. 1960. Molecular interactions in β-lactoglobulin, II: Ultracentrifugal and electrophoretic studies of the association of β-lactoglobulin below its isoelectric point. J. Am. Chem. Soc. 82 3161–3168. [Google Scholar]
- Uhrínová, S., Smith, M.H., Jameson, G.B., Uhrín, D., Sawyer, L., and Barlow, P.N. 2000. Structural changes accompanying pH-induced dissociation of the β-lactoglobulin dimer. Biochemistry 39 3565–3574. [DOI] [PubMed] [Google Scholar]
- Venu, K., Denisov, V.P., and Halle, B. 1997. Water 1H magnetic relaxation dispersion in protein solutions: A quantitative assessment of internal hydration, proton exchange, and cross-relaxation. J. Am. Chem. Soc. 119 3122–3134. [Google Scholar]
- Wahl, P. and Timasheff, S.N. 1969. Polarized fluorescence decay curves for β-lactoglobulin A in various states of association. Biochemistry 8 2945–2949. [DOI] [PubMed] [Google Scholar]
- Wiesner, S., Kurian, E., Prendergast, F.G., and Halle, B. 1999. Water molecules in the binding cavity of intestinal fatty acid binding protein: Dynamic characterization by water 17O and 2H magnetic relaxation dispersion. J. Mol. Biol. 286 233–246. [DOI] [PubMed] [Google Scholar]
- Witz, J., Timasheff, S.N., and Luzzati, V. 1964. Molecular interactions in β-lactoglobulin, VIII: Small-angle X-ray scattering investigation of the geometry of β-lactoglobulin A tetramerization. J. Am. Chem. Soc. 86 168–173. [Google Scholar]