Genetic regulation of canine skeletal traits: trade-offs between the hind limbs and forelimbs in the fox and dog

Synopsis

Genetic variation in functionally integrated skeletal traits can be maintained over 10 million years despite bottlenecks and stringent selection. Here, we describe an analysis of the genetic architecture of the canid axial skeleton using populations of the Portuguese Water Dog Canis familiaris) and silver fox (Vulpes vulpes). Twenty-one skeletal metrics taken from radiographs of the forelimbs and hind limbs of the fox and dog were used to construct separate anatomical principal component (PC) matrices of the two species. In both species, 15 of the 21 PCs exhibited significant heritability, ranging from 25% to 70%. The second PC, in both species, represents a trade-off in which limb-bone width is inversely correlated with limb-bone length. PC2 accounts for approximately 15% of the observed skeletal variation, ~30% of the variation in shape. Many of the other significant PCs affect very small amounts of variation (e.g., 0.2–2%) along trade-off axes that partition function between the forelimbs and hind limbs. These PCs represent shape axes in which an increase in size of an element of the forelimb is associated with a decrease in size of an element of the hind limb and vice versa. In most cases, these trade-offs are heritable in both species and genetic loci have been identified in the Portuguese Water Dog for many of these. These PCs, present in both the dog and the fox, include ones that affect lengths of the forelimb versus the hind limb, length of the forefoot versus that of the hind foot, muscle moment (i.e., lever) arms of the forelimb versus hind limb, and cortical thickness of the bones of the forelimb versus hind limb. These inverse relationships suggest that genetic regulation of the axial skeleton results, in part, from the action of genes that influence suites of functionally integrated traits. Their presence in both dogs and foxes suggests that the genes controlling the regulation of these PCs of the forelimb versus hind limb may be found in other tetrapod taxa.

Introduction

Recent advances in computational tools for quantitative genetics have allowed the genetic analysis of complex, polygenic morphological traits (Barton and Keightly 2002; Doerge 2002; Glazierm et al. 2002; Darvasi 2005). We used these tools in conjunction with molecular genotyping to analyze the genetic basis of variation in the canine skeleton (Chase et al. 2002, 2004; Carrier et al. 2005; Trut et al. 2006; Lark et al. 2006a, 2006b). The dog, Canis familiaris, is one of the most morphologically diverse mammals (Hart 1995; Coppinger and Coppinger 2001; Young and Bannasch 2006). Sizes range from 2 kg (Chihuahua) to 80 kg (Bull Mastiff) and shapes can vary from Basset Hounds and Boxers to Greyhounds and Great Danes.

Previously, we analyzed independent combinatorial aspects of skeletal variation using principal component (PC) analysis (Chase et al. 2002; Carrier et al. 2005). PCs vary in a quantitative manner and can be subjected to genetic analysis. PC analysis reduces correlated sets of traits to independent (orthogonal) vectorial components, each of which can be characterized by the projection of the vector onto each of the traits (Venables and Ripley 2002). These “loadings” present the extent and direction (+ or −) of the trait’s contribution to the resulting vector.

In previous publications, we used this approach to identify variation in heritable constellations of canine skeletal traits (reviewed by Lark et al. 2006a). A surprising result of this analysis was the discovery that removal of the covariation involved in size (PC1) revealed variation in independent components of shape, suites of functionally integrated traits, each of which were controlled by genetic loci. Quantitative trait loci (QTLs) are regions of the genome that contain one or more genes that regulate PC variation (Darvasi 2005). Thus, genetic analysis of the Portuguese Water Dog led to identification of QTLs responsible for variation in shape defined by canine skeletal PCs composed of groups of functionally related traits. Each of these groupings appeared to vary along a trade-off axis forming a functional compromise between high production of force (as exemplified by the Pit Bull) and energy-efficient speed (as exemplified by the Greyhound). Examples include trade-offs between the skull and postcranial skeleton (Chase et al. 2002) as well as changes in the pelvis and limb bones (Carrier et al. 2005). Using phenotypic data derived from radiograms and polymorphic molecular markers (Simple Sequence Repeats or SSRs), we identified QTLs for these trade-offs. Data from foxes indicated that these trade-offs were ancient and could be identified in the silver fox (Vulpes vulpes), the silver color phase of the red fox, and a member of the outgroup species for the evolutionary lineages of modern canids that separated from C. familiaris 10 million years ago (Wayne 1993; Bardeleben et al. 2005).

Here we compare PCs derived from metrics of the forelimbs and hind limbs of Portuguese Water Dogs and silver foxes. We show that both species exhibit similar constellations of traits that affect very small amounts of variation along trade-off axes that partition function between the forelimbs and hind limbs. In most cases, these trade-offs though small in magnitude are heritable in both species and genetic loci regulating these trade-offs have been identified in the Portuguese Water Dog.

Methods

Phenotypes and genotypes

The Portuguese Water Dog (PWD) population has been described (Chase et al. 1999). It comprises dogs brought up and maintained in the homes of individual owners. Radiographs of individual dogs followed a standardized protocol carried out by individual veterinarians of the owners’ choice. X-rays for phenotypes as well as blood for DNA genotypes were obtained from owners of PWDs through the Georgie Project (K. Miller, director; http://www.georgieproject.com). Phenotypes (skeletal metrics from radiographs) and DNA genotypes (alleles of Simple Sequence Repeat—SSR—markers) were obtained from 463 PWDs. Methods for analyzing the radiographs and for genotyping DNA with SSR markers have been described in detail (Chase et al. 2002). Specific, easily recognized, landmarks were used to define bone dimensions. These landmarks were accurately recognized by three different people. All points were recorded by using the paths function of Adobe Photoshop and exported to an Excel spreadsheet. Lengths of path were adjusted for measurement error (removal of extreme outliers) and checked for systematic bias by any investigator. Missing values of particular bones were imputed by using multiple regression of all other metrics. The 21 metrics used here are: acetabulum span, calcaneus length, inner diameter of the femur, outer diameter of the femur, femur length, humerus length, inner diameter of the humerus, outer diameter of the humerus, rear foot in-lever length, metacarpal length, metatarsal length, lengths of the olecranon, pisiform and radius, inner diameter of the radius, outer diameter of the radius, tarsal length, tibial length, inner diameter of the tibia, outer diameter of the tibia, and span of the tarsal joint (see Chase et al. 2002 for X-ray images). Alleles of 724 SSR markers distributed over the 38 dog autosomes and the X chromosome were determined for 463 dogs. The average distance between markers is 3.6 Mb.

Radiographs of foxes were collected from four interrelated fox populations [Aggressive (n = 24), Tame (n = 190), F1 (n = 39), and Backcross to Tame (n = 201)] developed for the study of behavior and maintained at the fox farm of the Institute for Cytology and Genetics (ICG) in Novosibirsk, Russia (Trut 2001; Trut et al. 2006; Kukekova et al. 2006). Genotyping initiated in the backcross population is as yet insufficient for morphological QTL analysis.

Heritability

We estimated the heritability of each trait using the “polygenic” function of SOLAR (Sequential Oligogenic Linkage Analysis Routines; Almasy and Blangero 1998). This function uses information on consanguinity from pedigrees to estimate the additive genetic variance of a phenotype. For the PWD population a previously validated, 26-generation pedigree was used. For the fox population we used the four-generation pedigree of the backcross population.

QTL detection

We used two different methods to identify QTLs: (1) allele sharing and (2) best linear unbiased estimates (BLUE) of genotypic means. The first is implicitly additive and has maximum power to detect QTLs that have an additive expression in the population. The second is capable of detecting any form of QTL expression (e.g., epistatic, dominant) but is less powerful for additive QTLs of small effect. In both cases, we estimated the significance of the association between the marker and the phenotype using Monte Carlo simulations (Manly 1997).

Allele sharing

Allele sharing associations between markers and traits were detected using the correlation of allele sharing at a marker with the phenoytpic similarity (Haseman and Elston 1972). Allele sharing values between pairs of dogs for each marker were first corrected for the mean across all pairs and for consanguinity between pairs (Ritland 1996). The residual sharing values were investigated for significant correlation with the phenotypic similarity. Monte Carlo simulations (Manly 1997) of a randomly generated dummy trait with heritability equal to the target phenotype were used to estimate the null distribution of the marker–phenotype association. This null distribution was used to estimate the significance of the association between the marker and the target phenotype. P-values were adjusted for ~700 markers tested.

Estimation of QTL means

We used a mixed model to estimate the QTL means (Kennedy et al. 1992). We assume that all of the background genetic effects are additive and use the model:

$$y_{ij}=g_i+a_{ij}+e_{ij},$$

where y_ij is the phenotype of the j-th individual of genotype i, g_i is the effect of genotype i, a_ij is the effect of the additive genetic background, and e_ij is the environmental deviation. The effects of the genotypes (g_i) are treated as fixed effects; the additive genetic background (a_ij), and environmental deviations (e_ij) are treated as random effects. The BLUE of the genotypic means is given by:

$$\text{G}={({\text{X}}^{\text{T}}{\text{V}}^{-1}\text{X})}^{-1}{\text{X}}^{\text{T}}{\text{V}}^{-1}y,$$

where X is the design matrix of 1s and 0s indicating the genotype of the individual, V is the covariance matrix for the vector of phenotypes, y;

$$\text{V}={\sigma }_{\text{A}}^2\text{A}+{\sigma }_{\text{E}}^2\text{I}$$

${\sigma }_{\text{A}}^2$ , the additive genetic variation, was estimated using the polygenic function of SOLAR (Almasy and Blangero 1998); A is the additive genetic relationship matrix, where A_ij = 2σ_ij (twice the coefficient of consanguinity (Falconer and Mackay 1996)); ${\sigma }_{\text{E}}^2$ is the environmental variance; and I is the identity matrix.

The ratio of the variance of the estimated genotypic means to the variance of the total phenotype was used as a test statistic. We estimated the significance of this statistic using Monte Carlo simulations in which a random trait of the same heritability was simulated using the known pedigree. The distribution of the test statistic under the null model was estimated as the beta distribution with the best fit to a set of 5000 simulations. The P-value of each marker was estimated as the cumulative probability of the null distribution exceeding the observed value.

Bootstrap analysis of PC loadings

PC analysis (Venables and Ripley 2002) defines independent factors (eigenvectors or loadings) that describe a decreasing amount of the total variation. The interpretation of these eigenvectors is important in exploring the biology underlying these patterns of variation. The magnitude of the loadings and their relative signs (correlation or inverse correlation) describe the influence of different measured traits on PCs determining size or shape. We used bootstrap analysis (Manly 1997) to determine confidence intervals about the individual trait loadings for each eigenvector as follows:

1. Run the principal component analysis (PCA) on the total set using the prcomp (Venables and Ripley 2002) function in the R program (see http://www.R-project.org). This defines the “best” eigenvectors (PCs), which will be used as standards for comparison to the bootstrap trials.

2. Randomly select, with replacement, a set of individuals (dog or foxes) equal in number to the original set.

3. Run PCA on this random set.

4. Find the PC that best matches (highest correlation with) each of the original PCs and record the loadings.

5. Repeat steps 2, 3 & 4, 500 times.

The resulting lists of trait loadings for each principal component give an estimate of the confidence intervals about the “best” trait loadings from the original data. Patterns defined by the “best” PCs, which are consistent with most of the data, will reappear in most of the bootstrap trials. Important trait loadings should remain significant—i.e., confidence intervals should not include 0. Here we use a threshold of 2 SE (95%) and 3 SE (99%) for significance.

Results

Twenty one metrics taken from radiographs of the forelimbs and hind limbs of the silver fox and PWD were used to construct separate anatomical principal component (PC) matrices of the two species (see Methods section). Table 1 presents the percent variation of each of the 21 PCs for the dog and for the fox, together with their heritabilities (see Methods section).

Table 1.

Parameters of dog and fox limb Principal Components (PC)

	Proportion of Variance		Dog		Fox
PC	Dog	Fox	h2	P-value	h2	P-value
1	0.580	0.503	0.70	0.0000	0.4575	0.0000
2	0.124	0.148	0.76	0.0000	0.5192	0.0000
3	0.053	0.049	0.62	0.0000	0.4218	0.0000
4	0.035	0.045	0.47	0.0000	0.4539	0.0000
5	0.029	0.039	0.21	0.0061	0.4513	0.0000
6	0.027	0.037	0.61	0.0000	0.3116	0.0045
7	0.024	0.027	0.38	0.0000	0.2937	0.0005
8	0.019	0.026	0.40	0.0000	0.4399	0.0001
9	0.018	0.021	0.25	0.0011	0.4052	0.0001
10	0.017	0.020	0.39	0.0000	0.0516	0.3335
11	0.015	0.017	0.40	0.0000	0.2428	0.0126
12	0.013	0.015	0.23	0.0005	0.3563	0.0000
13	0.011	0.011	0.22	0.0308	0.3651	0.0000
14	0.009	0.008	0.34	0.0008	0.4358	0.0000
15	0.005	0.007	0.23	0.0516	0.1598	0.0413
16	0.005	0.006	0.45	0.0000	0.0000	0.5000
17	0.004	0.005	0.19	0.0045	0.3779	0.0001
18	0.004	0.004	0.31	0.0002	0.2161	0.0041
19	0.004	0.004	0.04	0.2171	0.3250	0.0005
20	0.002	0.003	0.00	0.5000	0.0971	0.0965
21	0.002	0.003	0.39	0.0000	0.4124	0.0000

Proportion of variance explained and heritability. The 21 PCs are listed together with the fraction of the total variation that each explains, as well as the heritability (h²) of each. Heritabilities of marginal significance are italicized. Lack of heritability is indicated by bold type.

For the dog, 15 of the PCs showed significant heritability and an additional four were marginally heritable (italics). Only two, PCs 19 & 20 (bold), showed no heritability. Similarly, 15 of the fox PCs were significantly heritable and another three (italics) were marginally heritable. Fox PCs 10, 16, and 20 were clearly not heritable (bold). Significant heritabilities ranged from 70% to 25%.

In addition, QTLs could be identified in the dog population. These are shown in Fig. 1. Significant PC QTLs were identified on 19 of the 38 autosomes and more may be expected as marker coverage is improved for the genotyped population.

Fig. 1.

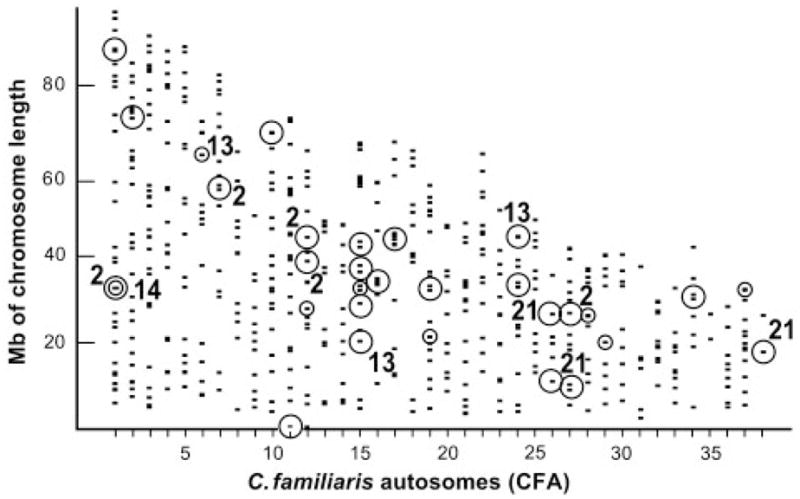
QTLS identified for limb PCs in the dog. The physical map positions (y-axis) for all SSR markers used (−), are identified on the 38 dog autosomes (CFA 1–38) arrayed on the x-axis. QTL positions are indicated at genome-wide threshold levels of P<0.05 (o) and P<0.01 (○). QTLs for specific PCs discussed in the text are labeled with their PC number.

PC1, or size, accounted for 50–58% of the variation. Other components represented different aspects of shape that could be characterized by the trait loadings for each component. A comparison between the dog and fox demonstrates that many of the PCs represent variations in shape that have been maintained over more than 10 million years of evolution, despite the extremely stringent selective bottlenecks of domestication and selection of breeds.

In both species, PC 2 and PC 21 represent the largest (12–15%) and smallest (0.2–0.3%) components of variation other than size. One might expect PC 21 to be an artifact of statistical noise. Evidence that PC 21 represents variation of a real phenotype (as opposed to nonspecific variation or “noise”) comes from comparing values for PC 21 computed separately from metrics of the right and left fox limbs. Figure 2 presents this right versus left correlation both for fox PC 2 and fox PC 21. If PC 21 were an artifact, we would expect no correlation between right and left values. It can be seen that the correlation for PC 21 is almost as good as that for PC 2. Moreover, both PC 2 and PC 21 are highly heritable (ranging from h² ~0.75 for PC 2 in the dog to h² ~0.4 for PC 21 in the dog and fox).

Fig. 2.

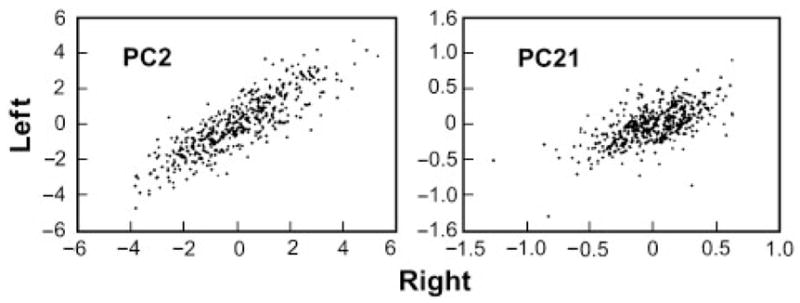
Correlations between the PC values obtained using sets of metrics from the right or the left limbs of the fox.

Table 2 presents loadings of PC 2 and PC 21 that characterize these PCs in the dog and fox. It can be seen that PC 2, in both species, represents a trade-off in which limb width is inversely correlated with limb length, accounting for about 12–15% of the total variation or ~30% of the variation in shape. The loading patterns that characterize this PC are extremely robust: bootstrap analysis indicates that these loading patterns will be obtained in more than 99 out of 100 trials, and five QTLs for PC 2 have been identified in the dog located on autosomes CFA 1, 7, 12, and 27 (Fig. 1). (See Fig. 4 of Lark et al. 2006b, for details of phenotypic effects of CFA 12 QTL genotypes).

Table 2.

Trait loadings for dog and fox PCs 2 and 21

	Dog		Fox
	PC2	PC21	PC2	PC21
	12.4%	0.2%	14.8%	0.3%
r(L)	−0.30	−0.68	−0.16	−0.59
m(L)	−0.27		−0.16
f(L)	−0.25		−0.15
t(L)	−0.26	0.6	−0.15	0.29
h(L)	−0.25	0.2	−0.12	0.52
f OD	0.18		0.24
f ID	0.32		0.40
h OD	0.25		0.27
h ID	0.38		0.43
r OD	0.22		0.25
r ID	0.29		0.37
t OD	0.14		0.13
t ID	0.28		0.37

The traits are listed to the left as radius (r), metatarsal (m), femur (f), tibia (t) and humerus (h) lengths (L), outer diameter (OD) and inner diameter (ID) (e.g., radius length: r(L); radius outer diameter r(OD); radius inner diameter r(ID). The percent variation for each PC heads a column listing the loadings for each trait.

In contrast, PC 21 a trade-off between the length of the radius and the length of the tibia and humerus, represents a minor fraction of the total variation, ~0.2%. However, variation in the length of the radius occurs in >99% of subsamples in both the dog and the fox, and in the dog an inverse correlation with the length of the tibia is similarly robust. In the fox, a similar inverse correlation with the tibial length is observed but it is somewhat less robust, occurring between the radius and tibia length in subsamples somewhat more frequently than 95% of the trials. In both fox and dog, inverse correlations of the radius with the humerus are observed with a frequency of better than 95% of subsampling trials.

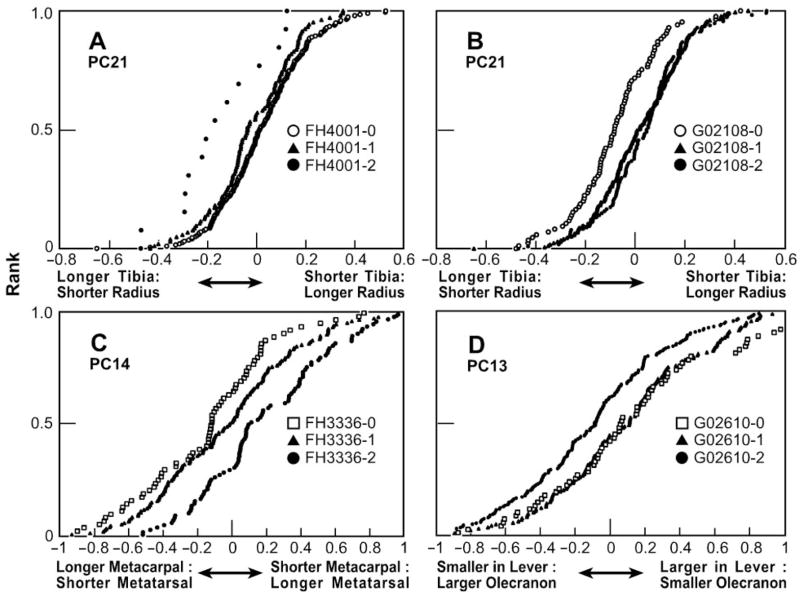
Finally, three QTLs have been identified in the dog for PC 21 on autosomes CFA 26, 27, and 38 (Fig. 1) and the relationships between genotype and phenotype for two of these QTLs are presented in Fig. 3A and B for the CFA27 and CFA38 QTLs, respectively. The phenotype of the QTL on CFA27 appears to be recessive (two copies of the marker allele with which the phenotype is associated are required for phenotypic expression). In contrast, the phenotype of the CFA38 QTL is dominant.

Fig. 3.

Phenotypic expression of dog QTL genotypes that regulate expression of PC21 (A, B), PC14 (C) and PC13 (D). QTLs shown are identified in Fig. 1: (A) PC21 QTL on CFA 27 marker FH4001 bp9855710-9855969; (B) PC21 QTL on CFA 38 marker G02108 bp17539884-17540056; (C) PC14 QTL on CFA 1 marker FH3336 bp34372926-34373176; (D) PC13 QTL on CFA 15 marker G02610 bp20045598-20045733; The trade-off axis of phenotypic variation is presented on the abscissa as the increasing value of the PC centered around a mean of 0. Dogs are ranked cumulatively in order of increasing PC value. Genotypes are classified according to association with zero (open circles or squares), one (heterozygote; filled triangle), or two (homozygote; filled circle) copies of the relevant SSR marker allele.

The heritability of PC 21 in both the fox and the dog, the correlation between the left and right PC 21 values, and the identification of regulating QTLs in the dog compel the conclusion that this small amount of skeletal variation represents an hereditary variation in shape that has been preserved over the evolutionary history that separates foxes and dogs.

Additional heritable effects contrasting the forelimbs and hind limbs

The inverse correlation between forelimb length and hind limb length that occur in both fox and dog PC 21 is found in other aspects of shape that characterize the front and rear limbs of dogs and foxes.

In another PC, the lengths of the metacarpal and metatarsal bones also are inversely correlated (Table 3). These constitute extremely robust loadings of dog PC 14 and fox PC 15. Both PCs are significantly heritable (Table 1) and a QTL has been identified on CFA 1 of the dog (Fig. 1). Figure 3C presents details of this dog PC 14 QTL. Although the relevant allele cannot be recessive, the data do not allow distinguishing between a dominant or additive mode of inheritance.

Table 3.

Trait loadings for dog PC14 and fox PC 15

	Dog	Fox
	PC14	PC15
	0.90%	0.70%
Metacarpal	0.37	0.32
Metatarsal	−0.72	−0.56

The percent variation for each PC is shown together with the loadings for the lengths of the metacarpal and metatarsal.

Cortical thickness also contrasts the fore and hind limbs in both the dog and the fox. PC 20 in the dog and PC 18 in the fox describe an inverse correlation between the cortical thickness of the humerus and the femur (Table 4). These account for between 0.4% and 0.8% of the variation in shape (0.2—0.4% of the total variation if size is included). In both species, the cortical thickness in the foreleg is inversely correlated with that of the hind leg. In the fox, however, this PC is heritable (22%; Table 1) whereas in the dog it is not. Another PC in the fox, PC 13, characterizes a similar relationship of the distal rear limb and forelimbs. This inverse correlation between cortical thickness of the radius and the tibia is highly heritable (37%; Table 1) and accounts for ~1% of the total variation. No such PC was found in the PWD.

Table 4.

Trait loadings for dog PC20 and fox PCs 13 and 18

	Dog	Fox
	PC20	PC13	PC18
	0.2%	1.1%	0.4%
r ID		0.39
r OD		−0.40
t ID		−0.35
t OD		0.27
f ID	0.50		0.44
f OD	−0.54		−0.42
h ID	−0.37		−0.34
h OD	0.4		0.26

Percent variance is shown as in Tables 2 and 3, together with the loadings for the inner diameter (ID) and outer diameter (OD) of the radius (r), tibia (t), femur (f) and humerus (h).

Finally, inverse correlations were observed between lever arms on the fore and hind legs. Table 5 presents results for PC 13 in the dog and PC 14 in the fox with inverse correlations between metrics (loadings) of the olecranon (i.e., muscle lever of elbow) and the in-lever or calcaneous (i.e., muscle levers of the ankle joints of the dog and fox, respectively). Again, these inverse correlations were highly heritable in both species (Table 1) and three QTLs were identified in the dog, on autosomes CFA 6, 15, and 24. Variation between haplotypes of the dog PC 13 QTL on CFA 24 is presented in Fig. 3D. In this case, a recessive mode of inheritance has been established. Whereas the fore–hind relationship in the dog involved the olecranon in the forelimb and the muscle in-lever in the hind limb, a somewhat different relationship was found in the fox, involving the calcaneous on the hind limb. The in-lever is, in fact, a part of the calcaneous, posterior to the ankle joint. The portion of the calacaneous anterior to the ankle joint is part of the out-lever, of which the main portion is the metatarsal. It is noteworthy that PC 17 in the dog and PC 19 in the fox (Tables 1 and 5) represent a trade-off between the in-lever and the calcaneous of which the in-lever is a part. Although the variation involved is small, it is heritable and represents a trade-off between the in-lever and out-lever functions of the calcaneous; like PC 2, this is a trade-off between generation of force (power) and speed (velocity). This suggests that in the fox, the olecranon is involved in a trade-off involving the ankle out-lever of the hind limb, in contrast to the dog in which the trade-off involves the in-lever.

Table 5.

Trait loadings for dog PCs13 and 8 and fox PCs 14 and 12

	Dog			Fox
	PC13	PC17	PC8	PC14	PC19	PC12
	1.1%	0.4%	1.9%	0.8%	0.4%	1.5%
Calcaneous		−0.48		0.2	−0.53
In-lever	0.27	0.3	0.25		0.4	0.31
Olecranon	−0.71			−0.73
Pisiform			−0.47			−0.35

Percent variance is shown as in Tables 2 and 3, together with the loadings for the calcaneous, in-lever, olecranon, and pisiform.

A separate relationship was identified between the ankle in-lever and the pisiform (i.e., muscle lever of wrist joint) (Table 5). PC 8 in the dog and PC 12 in the fox, both show this inverse correlation involving PCs different from those in which the olecranon is a participant. These PCs also are heritable in both species, although, as yet, we have not identified QTLs associated with PC 8 in the dog. Again the variation explained by these muscle-lever-arm PCs is small (1–2% of the total variation) but clearly significant.

Discussion

Previously (Chase et al. 2002; Carrier et al. 2005; Lark et al. 2006b), we presented evidence for skeletal changes in the functional morphology of the PWD that regulated a compromise between energy efficient speed (as in pursuit hounds) and force and agility (as in the Pit Bull, Mastiff, or Bulldog). The variation along this axis involved several principal components of skeletal shape including inverse correlations between metrics of the skull and postcranial skeleton, of the pelvis and limb bones, as well as various aspects of skeletal width and length. Preliminary results (Trut et al. 2006) indicated that similar trade-offs are present in the silver fox, a member of a sister lineage to dogs, representing a temporal phylogenetic separation of 10 million years. PC 2, an example of the trade-off that involves bone length versus bone width, as well as the inverse correlation of the calcaneous and ankle in-lever, both described here, are examples of this trade-off between speed and force. In the PWD, several QTLs regulate PC 2 (Fig. 1) including one on CFA 12 that regulates more than 20% of this aspect of limb–bone variation (for details see Fig. 4 of Lark et al. 2006b). These aspects of variation in shape are supportive of paedomorphic genetic control (Wayne 1986, 2001) in which juvenile aspects of morphology may be retained in the adult form to favor high production of force as opposed to the development of more gracile, speed efficient, adult forms (Chase et al. 2005; Carrier et al. 2005; Lark et al. 2006a).

Domestic dogs and silver foxes also appear to share a set of regulatory pathways that produce inverse relationships between the skeletal structures of the forelimb versus the hind limb. The retention of these small differences suggests that they are important. An increase in size of an element of the forelimb is associated with a decrease in size of an element of the hind limb and vice versa. This type of trade-off, forelimb and hind limb, was observed in the lengths of the long bones (i.e., PC 21 of PWDs and foxes; PC 14 of PWDs; PC 15 of foxes), the inner and outer diameters of long bones (i.e., PC 20 of PWDs; PCs 13 and 18 of foxes), and moment arms of extensor muscles (i.e., PCs 13 and 8 of PWDs and PCs 14 and 12 of foxes). Surprisingly, these patterns do not appear to be a simple consequence of ontogenetic allometries that have been described for domestic dogs by Wayne (1986).

It is noteworthy that these PCs are independent morphological components under, for the most part, independent genetic regulation (Fig. 1). This is similar to the various independent genetic controls that were found to regulate the morphological variation involved in the speed–force axis, but contrasts with the more global genetic control associated with regulating the lengths and widths of both fore and hind limbs seen in PC2. One result may be to increase the potential for a greater variety of limb functions associated with minor variations in shape.

These inverse relationships suggest a functional integration of the fore and hind limbs that has not been recognized previously. Biomechanists and functional morphologists have viewed limb musculo-skeletal systems from either of two perspectives: that the forelimbs and hind limbs function largely as relatively autonomous units (e.g., Carrier et al. 1998) or that they operate in an integrated fashion to effect locomotion (Heglund et al. 1982; Full et al. 1991; Jindrich and Full 1999; Lee and Meek 2005). The results of this genetic analysis suggest that the skeletal structure of the forelimbs and hind limbs may be developmentally tied to fore–hind functional trade-offs. There are a number of well-recognized “divisions of labor” between the forelimbs and the hind limbs: acceleration versus braking in terrestrial locomotion (Heglund et al. 1982; Full et al. 1991); support of body weight against gravity (Gray 1968; Lee et al. 2004); manipulation versus grooming; and change of body orientation versus propulsion in turning (Jindrich and Full 1999; Walter 2003). These and possibly other divisions of labor, involving balance, may hold explanations for the inversely correlated relationships observed here.

It is not surprising that a fundamental variation in functional morphology, such as the trade-off between length and width that characterizes PC 2, has been retained over 10 million years despite the selective bottlenecks of domestication and breed selection. However, the retention of trade-offs involving small amounts of variation between the forelimbs and hind limbs, described in Tables 2–5, was unexpected. Two explanations may be offered for this retention of variation during the evolutionary period that separates foxes and dogs: (1) Disruptive selection, Rueffler et al, 2006 may have maintained variation in the process of accommodating adaptation to different tasks or functions such as those discussed above; or (2) the genes involved may be intrinsically variable as proposed by Fondon and Garner (2004) preserving small differences in anatomy that might escape notice despite breed selection.