Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2009 Jun 1.
Published in final edited form as: J Hum Evol. 2008 Apr 3;54(6):909–914. doi: 10.1016/j.jhevol.2008.02.009

Quantitative genetics of modern human cranial variation

Richard J Sherwood a,*, Dana L Duren a, Ellen W Demerath b, Stefan A Czerwinski a, Roger M Siervogel a, Bradford Towne a
PMCID: PMC2391308  NIHMSID: NIHMS48568  PMID: 18394677

Introduction

The anatomy and biology of the basicranial complex and its relationships to the other cranial complexes has long played a central role in functional and phylogenetic interpretations of the hominin fossil record. Cranial traits frequently populate character lists in phylogenetic analyses and are commonly described as comprising an anatomical or functional complex. Most often these traits are treated as individual independent characters of equal phyletic value. Implicit in such considerations, however, is the assumption that the genetic contribution to morphological variation is high and equivalent across traits, and that phenotypic and genetic correlations between traits, irrespective of their magnitude, introduce negligible confounding effects in phylogenetic reconstruction (Hlusko, 2004).

While the ability to quantify and assess phenotypic variation in craniofacial variables has seen significant advances in recent years, the extent to which genetic and nongenetic factors influence this variation is typically not addressed. A key component to understanding the influences environmental and genetic factors have on the evolution of the craniofacial complex is a solid foundation of detailed knowledge of the genetic components underlying the development of normal craniofacial variation in modern populations. The aim of the present study is to elucidate fundamental aspects of the genetic architecture of normal variation in the human craniofacial complex.

In the current context, genetic architecture refers to the characterization of: (1) the extent to which variation in a trait is under genetic control, and (2) the degree to which two traits are controlled by the same genes or set of genes. The first of these is the heritability (h2) of a trait, and the second is the genetic correlation (ρG) between traits. Heritability estimates provide important information regarding the potential evolutionary response of traits to selective forces—the rate of evolutionary change being determined by the product of the heritability and the selection coefficient (Lynch and Walsh, 1998). Genetic correlations provide a means for quantifying the shared effects of genes on two or more traits. Genetic correlations have become critical in understanding the phenotypic heterogeneity observed in many craniofacial syndromes (Cohen, 2002), and have significant implications for the evolution of the hominin craniofacial complex.

Human cranial variation: evidence from family-based studies

Craniofacial morphometrics of archaeological or museum osteological collections have provided the field of human evolution with a broad perspective of craniofacial variation. These studies, however, cannot address issues of the genetic influence on trait variation, or covariation between traits. In order to adequately approach such issues, a large number of individuals of known biological relatedness is necessary. One such population is the Fels Longitudinal Study, which includes over 3,000 individuals belonging to ~250 families. Participants of the Fels Longitudinal Study have been the focus of numerous research articles including many that have had significant anthropological and human evolutionary significance, such as several papers detailing the growth and development of cranial structures (Young, 1956, 1957; Garn et al., 1963; Lewis and Roche, 1972, 1974; Roche and Lewis, 1974, 1976; Roche et al., 1977; Lewis et al., 1982, 1985; Ohtsuki et al., 1982a,b) and a classic paper investigating ontogenetic changes in basicranial flexion (i.e., the saddle angle; Lewis and Roche, 1977). In this report we seek to continue and extend the analysis of the Fels Longitudinal Study cranial data by presenting the first quantitative genetic analysis of the cranial data available in the archives.

Materials and methods

Study sample

Data for the current study are from the Fels Longitudinal Study, the largest and longest running study of human growth and body composition change over the lifespan (Roche, 1992). This is a randomly ascertained cohort in that participating families were not selected for any specific feature or trait (including any craniofacial trait), and is, therefore, a study of normal variation in such traits. Study participants generally live in or near southwest Ohio and were born between 1929 and the present.

Craniofacial data were collected from lateral radiographs of 328 males and 279 females from 90 extended and nuclear families in the Fels Longitudinal Study (Lewis and Roche, 1977, 1988; Duren et al., 2003; Sherwood et al., 2003). All protocols were approved by the Institutional Review Board of Wright State University, Dayton, OH, USA, and subjects provided informed written consent to all procedures prior to participation.

Because the majority of individuals had serial data, the observation closest to the participant’s 18th birthday1 was chosen for analysis. Table 1 presents the age and sex distribution for the sample. A minimum age was set at 13 years because by this age primary growth changes have been achieved in the measures of the basicranium.

Table 1.

Sex and age distribution of the study sample

n Age (years)
Average (SD) Minimum Maximum
Males 328 27.86 (15.21) >13 73.2
Females 279 32.64 (15.25) >13 75.5
Total 607 28.41 (15.23) >13 75.5
Open in a new tab

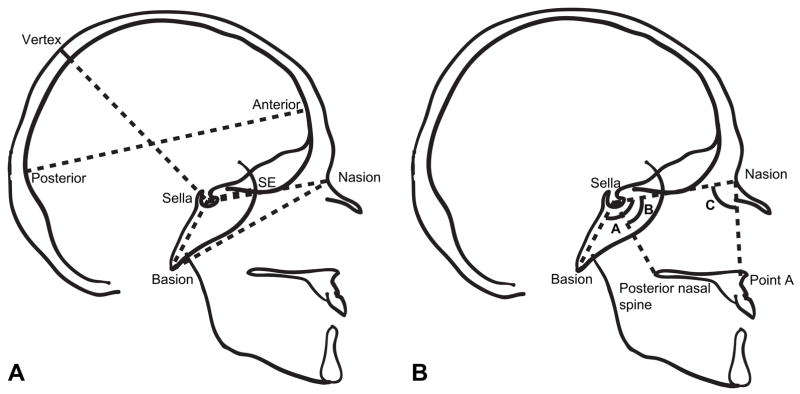
Lateral radiographs from participants were traced, and 10 craniometric points identified. Eight linear and three angular measurements were taken based on these points (Fig. 1; Table 2) and corrected for radiographic enlargement. The original craniofacial research program conducted on the Fels Longitudinal Study focused primarily on basicranial measures, such as anterior and posterior measures of basicranial length (sella-nasion and basion-sella respectively) and measures of basicranial angulation. In addition to basicranial measures, three neurocranial dimensions were collected. Neurocranial length was measured as the maximal anteroposterior dimension and two measurements of cranial height, from sella to vertex, were measured—one to the ectocranial margin and one to the endocranial margin. A measure of cranial thickness was calculated by subtracting these two cranial height measures.

Fig. 1.

Fig. 1

Open in a new tab

Linear (A) and angular (B) measures taken from human radiographs. Angle A = Ba-S-N; angle B = N-S-PNS; angle C = S-N-A.

Table 2.

Cephalometric measurements

Basion-sella Angles
Basion-nasion Nasion-sella-basion
Sella-nasion Sella-nasion-point A
Sella-sphenoethmoidale Nasion-sella-posterior nasal spine
Sella-vertex
Posterior-anterior length
Cranial thickness
Open in a new tab

All the radiographs were traced by a single individual. Reliability of measurements was examined by calculating the difference in repeated measures of radiographs by a single or multiple observers. Intra- and interobserver reliability for craniofacial studies based on the Fels Longitudinal Study radiographs was high with differences averaging 0.10 and 0.12 mm, respectively, for linear measures and 0.15 and 0.25 degrees for angular measures. (Lewis and Roche, 1972, 1974, 1977, 1988; Lewis et al., 1985).

Narrow sense heritability, the proportion of phenotypic variance attributable to additive genetic effects, was estimated for each measure using Sequential Oligogenic Linkage Analysis Routines (SOLAR v2.1.2, available online at: http://www.sfbr.org/solar/; Almasy and Blangero, 1998). SOLAR uses a maximum-likelihood variance components method that incorporates all familial information for parameter estimation. The significance of heritability estimates was tested by comparing the likelihoods of nested models using the likelihood ratio test. Variables examined for covariate effects included age, sex, and their interactions. To estimate the effects of these covariates on the study traits, each was screened in SOLAR by comparing the likelihood of a model that included the covariate to the likelihood of a model that excluded the covariate. Only the covariates significant at the p < 0.10 level were retained in the final model for each craniofacial trait.

Bivariate quantitative genetic analyses were conducted to examine the nature of shared genetic effects on different craniofacial traits. Using bivariate methods in the SOLAR analytic platform, the phenotypic correlations between the two traits were partitioned into additive genetic and random environmental components as given in equation 1:

ρP=ρGh12h22+ρE1−h121−h22 [1]

where ρP is the phenotypic correlation, ρG is the genetic correlation, ρE is the environmental correlation between trait pairs, and h12 and h22 are the heritabilities of trait 1 and trait 2, respectively. Additive genetic correlations (ρG) can range from −1.0 to 1.0, where a value of 1.0 indicates complete positive pleiotropy (i.e., the same genes are affecting the two traits in the same manner), a value of zero between the traits indicates that different genes influence them, and a value of −1.0 indicates complete negative pleiotropy (i.e., genes acting to increase the value of one trait decrease the trait value of the other). A genetic correlation significantly different from both 0 and 1 (or −1) indicates incomplete pleiotropy, meaning that the two traits are influenced to some extent by the same genes or sets of genes, but that each trait also has a genetic basis unique from the other.

Results

Statistical power in quantitative genetic studies is not only influenced by sample size but also by pedigree configuration. As noted, SOLAR uses all familial information for parameter estimation by examining all relative pairings between individuals. Table 3 presents the relative pairs in our sample, showing that there are a total of 2,293 relative pairings among the 607 individuals in the study sample. The ability to fully utilize the information in extended pedigrees, as is available with the Fels Longitudinal Study, provides substantial power to detect the genetic influence on variation of cranial traits.

Table 3.

Relative pairings represented among 607 individuals from 90 families with lateral cranial radiographs

Relationship Degree of relationship n
Identical siblings 5
Parent-offspring 1st 608
Siblings 360
Grandparent-grandchild 2nd 141
Avuncular 317
Half-siblings 43
Grand avuncular 3rd 49
Half avuncular 4
1st cousins 356
1st cousins, once removed 193
1st cousins, twice removed 5th 3
2nd cousins 157
2nd cousins, once removed 6th 31
3rd cousins 7th 26
Total 2,293
Open in a new tab

Heritability estimates and their standard errors for craniofacial traits are presented in Table 4. Heritabilities for all measurements were significant at the p < 0.001 level. Significant covariates included age and sex for most traits. Heritability estimates for basicranial traits ranged from moderate (e.g., basion-sella; h2 = 0.34) to high (e.g., sella-nasion; h2 = 0.71). Heritability estimates for neurocranial measures ranged from moderate (posterior–anterior; h2 = 0.45), to high (sella-vertex; h2 = 0.65). Heritability estimates for angular measurements were moderate to high, with basicranial flexion (basion-sella-nasion; h2 = 0.60) and the angle of facial positioning sella-nasion-point A, (h2 = 0.54) being slightly more heritable than the angle from nasion-sella-posterior nasal spine (h2 = 0.41).

Table 4.

Heritability estimates (h2) and standard errors for craniofacial traits. Significant covariates are indicated

h2 S.E. Covariates
% Vara pb
Age Sex Age × sex Age2 Age2 × Sex
Basion-sella 0.34 0.08 ● ● 26 <0.001
Basion-nasion 0.53 0.07 ● ● 33 <0.001
Sella-nasion 0.71 0.06 ● ● ● 30 <0.001
Sella-sphenoethmoidale 0.55 0.07 ● 11 <0.001
Sella-vertex (ectocranial) 0.65 0.07 ● ● 18 <0.001
Posterior-anterior 0.45 0.08 ● ● ● 23 <0.001
Cranial thickness 0.48 0.09 ● ● 7 <0.001
Ba-S-N angle 0.60 0.07 ● ● 3 <0.001
S-N-pt. A angle 0.54 0.09 ● ● 0.5 <0.001
N-S-PNS angle 0.41 0.07 ● ● 1.6 <0.001
Open in a new tab
a

Percent variation of trait explained by significant covariate effects.

b

h0: h2 = 0.

Because each craniofacial measure was found to be significantly influenced by genetic factors, a genetic correlation matrix was calculated in order to evaluate the nature of shared genetic influences between traits. Table 5 presents the additive genetic correlation matrix for all measures. All genetic correlations were significantly less than 1.0, with a number of trait pairs showing complete genetic independence from each other (i.e., genetic correlation not significantly different from zero). The genetic correlations between the remaining traits were significantly different from both 1.0 and zero, indicating a state of incomplete pleiotropy; that is, these traits are influenced by both shared and unique sets of genes. As not all traits were genetically correlated with all other traits, it is possible to define correlation sets for each measure. For example, measurement of the posterior base (basion-sella) was significantly genetically correlated with three traits: basicranial flexion (basion-sella-nasion; ρG = −0.33), total basicranial length (basion-nasion; ρG = 0.52), and facial positioning (sella-nasion-point A; ρG = −0.37). Anterior basicranial length (sella-nasion), was significantly genetically correlated with five traits: basion-nasion, (ρG = 0.84); sella-sphenoethmoidale, (ρG = 0.52); posterior-anterior length, (ρG = 0.28); cranial thickness, (ρG = 0.31); and the angle nasion-sella-posterior nasal spine, (ρG = −0.47). Correlation sets may overlap, to varying degrees, with genetic correlation sets defined by the other traits. For instance, in the examples given, basion-nasion is significantly genetically correlated with both posterior and anterior basicranial length.

Table 5.

Genetic correlation (ρG) matrix

Ba-S Ba-N S-N S-Se S-Vx P-A CT Ba-S-N S-N-pt. A
Basion-nasion 0.52a (0.10)
Sella-nasion 0.20 (0.13) 0.84a (0.04)
Sella-sphenoethmoidale −0.13 (0.13) 0.34a (0.11) 0.52a (0.08)
Sella-vertex (ectocranial) −0.24 (0.13) 0.18 (0.11) 0.15 (0.10) 0.06 (0.11)
Posterior-anterior −0.15 (0.16) 0.17 (0.12) 0.28a (0.10) 0.26 (0.13) 0.81a (0.06)
Cranial thickness 0.31 (0.16) 0.43a (0.12) 0.31a (0.11) 0.28a (0.14) 0.24a (0.12) 0.09 (0.16)
Ba-S-N angle −0.33a (0.12) 0.26a (0.10) 0.03 (0.10) 0.10 (0.11) 0.39a (0.10) 0.08 (0.13) 0.04 (0.13)
S-N-pt. A angle 0.37a (0.15) −0.04 (0.13) −0.02 (0.12) −0.16 (0.13) −0.27a (0.11) 0.05 (0.15) −0.10 (0.15) −0.49a (0.10)
N-S-PNS angle −0.07 (0.16) −0.14 (0.13) −0.47a (0.09) −0.38a (0.11) 0.22 (0.12) −0.07 (0.14) 0.26 (0.14) 0.48a (0.11) −0.47a (0.12)
Open in a new tab
a

p < 0.05.

Discussion and conclusion

Craniofacial traits serve as the primary characters used in taxonomic assessment of fossil hominins. A full understanding of the sources of variation in such traits is essential for accurate phylogenetic reconstructions. Quantitative genetic approaches provide insight into the most evolutionarily salient of those sources—the extent to which trait variation is genetically influenced and the extent to which covariation of traits is due to the shared effects of genes.

We have demonstrated that all cranial traits examined in the current study are significantly heritable. Previous quantitative genetic studies have examined the craniofacial complex in humans (Byard et al., 1984, 1985a,b) and in non human primates (e.g., Cheverud and Buikstra, 1981a,b, 1982; Cheverud, 1982) and similarly found significant heritability of craniofacial traits. Standard errors were typically large for these studies and a percentage of heritability estimates were found to be insignificant. A likely factor in this was a reliance on less powerful study designs (i.e., mother-offspring or sibling designs). The current study is the first examination of the genetic architecture of the human cranium utilizing an extended pedigree design. Some pedigrees in the Fels Longitudinal Study include several hundred individuals spanning three generations or more. This configuration means that related individuals come from a variety of households and locales. This reduces possible effects of shared environments on traits (often a confounding factor in mother-offspring or sibling designs), thus yielding more accurate and reliable h2 and ρG estimates.

Genetic correlation analyses in the current study reveal that several traits share a common genetic basis while other traits show genetic independence from one another. It would be reasonable to assume that traits from an isolated region, such as the basicranium, would demonstrate significant levels of pleiotropy as indicated by significant genetic correlations between traits. The pattern of genetic correlations, however, presents a mosaic. Rather than identifying a common pattern of genetic correlations among basicranial traits, each trait is represented by a unique set of significant genetic correlations with a subset of traits. Ideally, traits are used in phylogenetic analyses as a surrogate for the underlying genetic architecture influencing variation and covariation in the traits of interest. The problems associated with the use of intercorrelated traits in phylogenetic analyses have frequently been discussed (e.g., Trinkaus, 1990; Hlusko, 2004). While there are multiple potential sources for intercorrelations, the use of genetically correlated traits may bias phylogenetic assessments by effectively reducing the genetic signal being analyzed.

Application to the fossil record

Characterizing trait variation is the cornerstone of phylogenetic analyses. Quantitative genetic analyses provide a unique opportunity to examine the genetic influences on variance of and covariance between traits. As many interpretations of the fossil record are based on analyses of comparative skeletal material from extant primates available in museum collections, it is reasonable to scrutinize the composition of those collections. Many of the specimens in museum collections represent multiple members from individual social groups and, depending upon mating patterns and transfer systems, will include individuals with close genetic relationships. It is clear from the results presented here that samples consisting of kin-groups affect estimates of population variation, especially from small samples. Therefore, samples from museum collections may contain a substantial bias, potentially influencing application to and interpretations of the fossil record. For traits with high heritability, measures of phenotypic variation are expected to be reduced within closely related individuals compared to variation between unrelated individuals. Similarly, analyses using correlation techniques (including techniques such as principal components analysis) will be biased by inflated estimates of correlation coefficients, if the relationships between individuals are not considered. Finally, analyses utilizing percentages of presence/absence in nonmetric traits, such as cuspal variations in teeth or cranial features such as emissary foramina or occipital/marginal sinus systems, may also be heavily biased if these traits are heritable.

In large collections it may be possible to reduce biases by enlarging the number of individuals used in analyses. Unless specific information regarding the details of specimen collection exist, however, it may not be possible to guarantee the familial independence of any sample. In the case of rare species where only small numbers of individuals are available, it may be assumed that only a single, or at most a few, family group(s) is(are) represented. For instance, in Albrecht’s (1982) inventory of primate skeletal material available in museum collections, there are 18 and 19 genera represented by 15 or fewer specimens in the American Museum of Natural History and National History of Natural Museum, respectively (two collections frequently used by researchers). Given the biases that may arise from use of such samples, it is important to consider the underlying relationship structure of the sample if possible, and acknowledge the potential bias.

Acknowledgments

The authors are indebted to the efforts of those who initiated and maintained the collection of craniofacial data from the Fels Longitudinal Study; in particular, Dr. Alex Roche and the late Dr. Arthur Lewis. We express our sincere gratitude to the participants of the Fels Longitudinal Study. This work was supported in part by the National Institute of Child Health and Human Development HD12252 to R.M. Siervogel, and the National Institute of Dental and Craniofacial Research (NIH) DE016692, DE016408 to R.J. Sherwood.

Footnotes

1

During the history of the study, occasional efforts were made to bring in relatives of serial participants (e.g., grandparents, aunts, etc.) for a single visit regardless of age. In these instances, that visit constituted the “observation closest to 18”, explaining the range of ages seen in the current sample.

References

  1. Albrecht G. Collections of nonhuman primate skeletal materials in the United States and Canada. Am J Phys Anthropol. 1982;57:77–98. [Google Scholar]
  2. Almasy L, Blangero J. Multipoint quantitative-trait linkage analysis in general pedigrees. Am J Hum Genet. 1998;62:1198–1211. doi: 10.1086/301844. [DOI] [PMC free article] [PubMed] [Google Scholar]
  3. Byard PJ, Poosha DV, Satyanarayana M, Rao DC. Family resemblance for components of craniofacial size and shape. J Craniofac Genet. 1985a;5:229–238. [PubMed] [Google Scholar]
  4. Byard PJ, Poosha DV, Satyanarayana M, Rao DC, Russell JM. Path analysis of family resemblance for cranio-facial traits in Andhra Pradesh nuclear families and twins. Annls Hum Biol. 1985b;12:305–314. doi: 10.1080/03014468500007831. [DOI] [PubMed] [Google Scholar]
  5. Byard PJ, Sharma K, Russell JM, Rao DC. A family study of anthropometric traits in a Punjabi community: II An investigation of familial transmission. Am J Phys Anthropol. 1984;64:97–104. doi: 10.1002/ajpa.1330640202. [DOI] [PubMed] [Google Scholar]
  6. Cheverud JM. Phenotypic, genetic, and environmental morphological integration in the cranium. Evolution. 1982;36:499–516. doi: 10.1111/j.1558-5646.1982.tb05070.x. [DOI] [PubMed] [Google Scholar]
  7. Cheverud JM, Buikstra JE. Quantitative genetics of skeletal nonmetric traits in the rhesus macaques on Cayo Santiago. I Single trait heritabilities. Am J Phys Anthropol. 1981a;54:43–49. doi: 10.1002/ajpa.1330540106. [DOI] [PubMed] [Google Scholar]
  8. Cheverud JM, Buikstra JE. Quantitative genetics of skeletal nonmetric traits in the rhesus macaques on Cayo Santiago. II Phenotypic, genetic, and environmental correlations between traits. Am J Phys Anthropol. 1981b;54:51–58. doi: 10.1002/ajpa.1330540107. [DOI] [PubMed] [Google Scholar]
  9. Cheverud JM, Buikstra JE. Quantitative genetics of skeletal nonmetric traits in the rhesus macaques of Cayo Santiago. III Relative heritability of skeletal nonmetric and metric traits. Am J Phys Anthropol. 1982;59:151–155. doi: 10.1002/ajpa.1330590205. [DOI] [PubMed] [Google Scholar]
  10. Cohen MM. Perspectives on craniofacial anomalies, syndromes, and other disorders. In: Lin KY, Ogle RC, Jane JA, editors. Craniofacial Surgery: Science and Surgical Technique. W.B. Saunders Company; Philadelphia: 2002. pp. 3–38. [Google Scholar]
  11. Duren DL, Czerwinski SA, Sherwood RJ, Roche AF, Siervogel RM, Towne B. Quantitative genetics of the craniofacial complex in humans. Am J Phys Anthropol. 2003;36(Suppl):91–92. [Google Scholar]
  12. Garn SM, Lewis AB, Vicinus JH. The inheritance of symphyseal size during growth. Angle Orthod. 1963;33:222–231. [Google Scholar]
  13. Hlusko LJ. Integrating the genotype and phenotype in hominid paleontology. Proc Natl Acad Sci. 2004;101:2653–2657. doi: 10.1073/pnas.0307678101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Lewis AB, Roche AF. Elongation of the cranial base in girls during pubescence. Angle Orthod. 1972;42:358–367. doi: 10.1043/0003-3219(1972)042<0358:EOTCBI>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  15. Lewis AB, Roche AF. Cranial base elongation in boys during pubescence. Angle Orthod. 1974;44:83–93. doi: 10.1043/0003-3219(1974)044<0083:CBEIBD>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  16. Lewis AB, Roche AF. The saddle angle: constancy or change? Angle Orthod. 1977;47:46–54. doi: 10.1043/0003-3219(1977)047<0046:TSACOC>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  17. Lewis AB, Roche AF. Late growth changes in the craniofacial skeleton. Angle Orthod. 1988;58:127–135. doi: 10.1043/0003-3219(1988)058<0127:LGCITC>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  18. Lewis AB, Roche AF, Wagner B. Growth of the mandible during pubescence. Angle Orthod. 1982;52:325–342. doi: 10.1043/0003-3219(1982)052<0325:GOTMDP>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  19. Lewis AB, Roche AF, Wagner B. Pubertal spurts in cranial base and mandible. Comparisons within individuals. Angle Orthod. 1985;55:17–30. doi: 10.1043/0003-3219(1985)055<0017:PSICBA>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  20. Lynch M, Walsh B. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Inc; Sunderland, MA: 1998. [Google Scholar]
  21. Ohtsuki F, Mukherjee D, Lewis AB, Roche AF. A factor analysis of cranial base and vault dimensions in children. Am J Phys Anthropol. 1982a;58:271–279. doi: 10.1002/ajpa.1330580305. [DOI] [PubMed] [Google Scholar]
  22. Ohtsuki F, Mukherjee D, Lewis AB, Roche AF. Growth of cranial base and vault dimensions in children. J Anthropol Soc Nippon. 1982b;90:239–258. doi: 10.1002/ajpa.1330580305. [DOI] [PubMed] [Google Scholar]
  23. Roche AF. Growth, Maturation and Body Composition: The Fels Longitudinal Study 1929–1991. Cambridge University Press; Cambridge: 1992. [Google Scholar]
  24. Roche AF, Lewis AB. Sex differences in the elongation of the cranial base during pubescence. Angle Orthod. 1974;44:279–294. doi: 10.1043/0003-3219(1974)044<0279:SDITEO>2.0.CO;2. [DOI] [PubMed] [Google Scholar]
  25. Roche AF, Lewis AB. Late growth changes in the cranial base. In: Bosma JF, editor. Symposium on Development of the Basicranium. U.S. Dept. Health, Education, and Welfare, NIH; Bethesda, MD: 1976. pp. 221–239. [Google Scholar]
  26. Roche AF, Lewis AB, Wainer H, McCartin R. Late elongation of the cranial base. J Dent Res. 1977;56:802–808. doi: 10.1177/00220345770560071501. [DOI] [PubMed] [Google Scholar]
  27. Sherwood RJ, Duren DL, Czerwinski SA, Blangero J, Towne B. Quantitative genetics of modern human craniofacial variation: implications for the interpretation of the hominin fossil record. Am J Phys Anthropol. 2003;36(Suppl):190. [Google Scholar]
  28. Trinkaus E. Cladistics and the hominid fossil record. Am J Phys Anthropol. 1990;83:1–11. doi: 10.1002/ajpa.1330830102. [DOI] [PubMed] [Google Scholar]
  29. Young RW. The measurement of cranial shape. Am J Phys Anthropol. 1956;14:59–72. doi: 10.1002/ajpa.1330140120. [DOI] [PubMed] [Google Scholar]
  30. Young RW. Postnatal growth of the frontal and parietal bones in white males. Am J Phys Anthropol. 1957;15:367–386. doi: 10.1002/ajpa.1330150316. [DOI] [PubMed] [Google Scholar]

RESOURCES