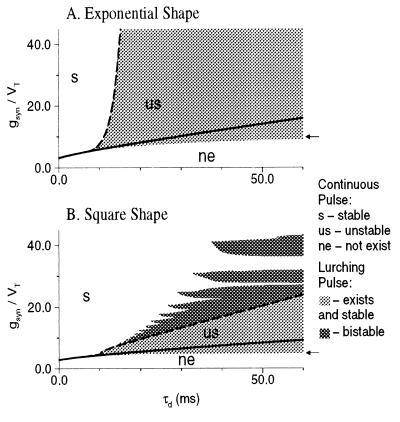
Figure 4.

Regimes of existence and stability of the continuous and lurching pulses in the τ_d-ν plane are shown in A for exponential footprint shape and in B for square footprint shape. Parameters are as in Fig 3. The boundaries of the regime in which the lurching pulse exists and is stable were computed from numerical simulations, in which a pulse was initiated by a “shock” initial stimulus; N = 20,000, ρ = 50. The solid line denotes the minimal possible velocity as a function of g_syn; the continuous pulse becomes unstable (via a Hopf bifurcation) on the dashed line. The continuous pulse is therefore stable above both the solid and long dashed line, as denoted by “s.” It is unstable between the two lines, as denoted by “us,” and does not exist below the continuous line, as denoted by “ne.” The light-gray shading represents the region for which lurching pulses (and not continuous pulses) are obtained. Bistable regimes, in which the continuous pulse can coexist with the lurching pulse, are denoted by the dark-gray shading. For the square footprint shape (B), but not for the exponential footprint shape, there is such a bistable regime that has a “tongue-like” structure. The arrow at the right of each graph represents the minimal values of g_syn for which the lurching pulse is found in simulations for τ_d → ∞.