Assessing Genetic Heterogeneity within Bacterial Species Isolated from Gastrointestinal and Environmental Samples: How Many Isolates Does It Take?

Abstract

Strain typing of bacterial isolates is increasingly used to identify sources of infection or product contamination and to elucidate routes of transmission of pathogens or spoilage organisms. Usually, the number of bacterial isolates belonging to the same species that is analyzed per sample is determined by convention, convenience, laboratory capacity, or financial resources. Statistical considerations and knowledge of the heterogeneity of bacterial populations in various sources can be used to determine the number of isolates per sample that is actually needed to address specific research questions. We present data for intestinal Escherichia coli, Listeria monocytogenes, Klebsiella pneumoniae, and Streptococcus uberis from gastrointestinal, fecal, or soil samples characterized by ribotyping, pulsed-field gel electrophoresis, and PCR-based strain-typing methods. In contrast to previous studies, all calculations were performed with a single computer program, employing software that is freely available and with in-depth explanation of the choice and derivation of prior distributions. Also, some of the model assumptions were relaxed to allow analysis of the special case of two (groups of) strains that are observed with different probabilities. Sample size calculations, with a Bayesian method of inference, show that from 2 to 20 isolates per sample need to be characterized to detect all strains that are present in a sample with 95% certainty. Such high numbers of isolates per sample are rarely typed in real life due to financial or logistic constraints. This implies that investigators are not gaining maximal information on strain heterogeneity and that sources and transmission pathways may go undetected.

Strain typing of bacterial isolates is widely used to identify sources of infection or contamination, to elucidate routes of transmission, or to show persistence of bacterial strains within hosts or environments (13, 22). The identification of sources of contamination is necessary to design intervention strategies aimed at reducing the risk of contamination (3, 6, 11). Often, the numbers of isolates that are genotyped in a study are based on convention, as well as limitations in time, funding, and storage capacity, rather than on a specified level of confidence about the total number of strains likely to be present in a sample. If too few isolates are analyzed per sample, vital information about the source of infection or contamination may be missed; analysis of too many isolates, on the other hand, is a waste of resources. While the detection of one isolate of a strain is sufficient to demonstrate the presence of that strain, the absence of a strain may be inferred with a certain degree of confidence only after a minimum required number of isolates from the sample are tested.

The required number of isolates in a sample that need to be typed in order to be 95% confident that all strains have been found can be derived from Bayesian inference (7). Bayesian sample size calculation combines prior information, based on expert opinion or pilot data sets from related studies, with data from additional typing studies to generate the posterior probability of detecting all strains that are present in a sample (1, 19). This study included data sets from the ruminant gastrointestinal tract and farm environments and allowed exploration of strain heterogeneity across bacterial species within sample types and across sample types within bacterial species. It continued the discussion initiated by Singer et al. (19) and Altekruse et al. (1) by showing that for different sources of samples different numbers of isolates need to be genotyped due to variability in the heterogeneity of bacterial populations. It demonstrated that the interplay between statisticians and microbiologists is essential for meaningful sample size estimation. Specifically, the aims of the current study were (i) to provide a single WinBUGS program code to perform all calculations with a large variety of data, (ii) to explain methods for the derivation of priors and the impact that they have on the posterior distributions, and (iii) to extend previously reported methodology (1, 19) by relaxing the assumption about equal expected relative frequencies of strains within samples.

MATERIALS AND METHODS

Sample collection, bacterial isolation, and strain typing.

In this paper, the terms “isolate” and “strain” are used in accordance with international standard definitions, as summarized by Zadoks and Schukken (22). The term “isolate” is used for a population of bacterial cells in pure culture derived from a single colony on an isolation plate and identified to the species level. The term “strain” refers to an isolate or a group of isolates exhibiting characteristics that set it apart from other isolates belonging to the same species. Strains can be identified using a variety of methods, including the presence of specified virulence markers (virulotyping) or evaluation of the overall heterogeneity of the bacterial genome (genotyping). Strain typing information was obtained for the following four bacterial species: Streptococcus uberis, a gram-positive pathogen that causes mastitis in dairy cattle; Listeria monocytogenes, a gram-positive food-borne pathogen; Klebsiella pneumoniae, a gram-negative pathogen that causes mastitis in dairy cattle and a range of clinical diseases in humans; and non-type-specific Escherichia coli, including verotoxinogenic E. coli (VTEC), a group that includes gram-negative food-borne and zoonotic pathogens. All four pathogens can be found in the feces of ruminants and in their environments (8, 16, 17, 18, 23). For the gram-positive species and Klebsiella spp., isolates from fecal and environmental samples were available from field studies, and data on strain heterogeneity in both types of samples were available from previous work (S. uberis) or were generated for the current analysis (L. monocytogenes, K. pneumoniae in soil). For the gram-negative species, fecal samples were available. For E. coli, additional samples were available from ovine feces and the ovine gastrointestinal tract, as well as bovine feces (Table 1). All isolates in the study were picked at random from agar plates.

TABLE 1.

Types and numbers of samples and typing methods used to obtain bacterial isolates and typing information for assessment of within-sample strain heterogeneity

Aim of statistical analysis	Organism	Source	No. of samples	Typing method (reference[s])a
Population heterogeneity across	S. uberis	Feces	16	Ribotyping (23)
species and sample types		Soil	9
	L. monocytogenes	Feces	10	PFGE (18)
		Soil	10
	K. pneumoniae	Feces	11	RAPD (17, 21)
Impact of priors	Ovine non-type-specific	Feces	50b	ERIC
	E. coli	Feces	88c	Fingerprinting
		Rumen	38	(12; D. Döpfer, unpublished data)
		Small intestine	10
		Large intestine	9
Sample size estimation for unequal relative frequencies of strains	Bovine non-type-specific E. coli, including VTEC	Feces	76d	PCR for virulence genes (4, 8)

^aPFGE, pulsed-field gel electrophoresis; RAPD, random amplified polymorphic DNA; ERIC, enterobacterial repetitive intergenic consensus sequence.

^bFive sheep were sampled daily for 5 days and again for 5 days after a 1-day interruption; the data set was used to generate a prior distribution.

^cFive sheep were sampled daily for 21 days (105 samples), but 17 samples were missing; the data set was used to calculate the posterior estimates for the sample sizes.

^dSeventy-six calves were sampled once, and 10 isolates of E. coli were screened for virulence markers (verotoxin 1, verotoxin 2, eae, and ehxA) for each sample.

To explore the heterogeneity of bacterial populations across sample types and bacterial species, sets of fecal and soil isolates belonging to three bacterial species were used. Isolates of S. uberis originated from soil samples and fecal samples that were collected on a dairy farm in New York State (23). For each soil sample, between four and eight isolates were characterized by automated ribotyping using restriction enzyme PvuII. For fecal samples, two to four isolates were analyzed after selective enrichment on indicator media (23). Isolates of L. monocytogenes were obtained from 10 fecal samples from dairy cattle and from 10 soil samples collected on ruminant farms (dairy cattle, beef cattle, sheep, or goats) in New York State (18). Strain typing of three or four isolates per sample was performed by means of pulsed-field gel electrophoresis using the PulseNet protocol, including restriction enzymes ApaI and AscI (9). Isolates of K. pneumoniae originated from fecal samples collected from dairy cattle in New York State. For each sample (n = 11), four isolates were selected for random amplified polymorphic DNA analysis (17). Isolates of the genus Klebsiella were also obtained from soil samples, but the number of isolates belonging to the species K. pneumoniae was insufficient for assessment of strain heterogeneity within samples (data not shown).

A second data set was used to compare the impact of relatively uninformative versus informative priors on outcomes of Bayesian sample size estimates. The isolates of non-type-specific E. coli, including VTEC, were obtained from fecal samples, rumen fluid, the small intestine (i.e., duodenum and ileum), and the large intestine (i.e., cecum and colon) of five sheep kept in indoor stalls. Feces samples were collected daily on days 1 to 21. Rumen fluid samples were collected 2 to 10 times for each animal at 1- to 7-day intervals using an esopharyngeal tube. One sample from the small intestine and one sample from the large intestine were collected from all animals at necropsy on day 21. Samples were stored at 4°C for a maximum of 12 h and homogenized, and 1:10, 1:100, and 1:1,000 dilutions were prepared using brain heart infusion broth (Difco). Portions (100 μl) of each dilution were plated on separate MacConkey agar plates and incubated at 37°C overnight, and E. coli was identified and counted as lactose-fermenting microorganisms using the dilution plates on which individual colonies were identifiable. For each sample five isolates of E. coli were genotyped using a PCR with enterobacterial repetitive intergenic consensus sequence primers (5).

Finally, to extend the methodology to samples in which strains were not assumed to be present at the same frequency, a set of bovine E. coli isolates was used. Seventy-six fecal samples were collected from 76 beef calves, and these samples represented the first samples in time, including 10 isolates screened for each sample from the longitudinal study reported by Geue et al. (8). For each sample, 10 isolates of E. coli (a total of 760 isolates) were screened for the presence of verotoxin 1 and verotoxin 2, for intimin, and for hemolysin using PCR tests as reported by Geue et al. and Döpfer et al. (4, 8). Of the 760 E. coli isolates, 425 (55.9%) were positive for verotoxin 1, verotoxin 2, or both verotoxins, 55 (7.2%) isolates were positive for verotoxin 1, verotoxin 2, or both verotoxins in combination with intimin, 124 (16.3%) isolates were positive for verotoxin 1, verotoxin 2, or both verotoxins in combination with the hemolysin, and 52 (6.8%) isolates were positive for intimin in combination with hemolysin. These four categories are not mutually exclusive. The average numbers of isolates in all of the isolates screened that were found to be positive for the combinations of virulence markers are shown in Table 2.

TABLE 2.

Overview of strain typing data: average numbers of isolates typed, average numbers of strains observed, assumed numbers of types per sample, α values used to construct the prior distributions, and numbers of isolates required to be typed in order to identify all strains present in a sample with 95% probability

Organism	Source	Typing methoda	Avg no. of isolates typed (SD)	Avg no. of strain types observed (SD)	No. of strains assumedb	α for the prior distribution	Required no. of isolates
S. uberis	Feces	Ribotyping	2.6 (0.6)	1.5 (0.7)	3	α1 … α3 = 1/3	10
	Soil	Ribotyping	5.9 (1.2)	3.9 (1.1)	5	α1 … α5 = 1/5	20
K. pneumoniae	Feces	RAPD	4.0 (0.0)	3.0 (0.8)	4	α1 … α4 = 1/4	15
L. monocytogenes	Feces	PFGE	3.5 (0.6)	2.1 (0.6)	4	α1 … α4 = 1/4	10
	Soil	PFGE	3.5 (0.5)	1.4 (0.5)	4	α1 … α4 = 1/4	6
Ovine non-type-specific	Fecesc	ERIC fingerprints	5.1 (1.0)	2.9 (1.2)	1 to 6b	α1, … α6 = fractionsb	14
E. coli	Feces		5.1 (0.8)	3.8 (1.1)	6	α1 … α6 = 1/6 or α1 … α6 = 1	16
	Rumen		4.3 (1.2)	1.7 (0.9)	5	α1 … α5 = 1/5	11
	Small intestine		5.0 (0.0)	1.3 (0.5)	5	α1 … α5 = 1/5	5
	Large intestine		5.0 (0.0)	1.8 (0.8)	6	α1 … α6 = 1/6	10
Bovine non-type-specific E. coli, including	Feces positive for V12d	PCR	10	5.6 (3.6)		α1 = α2 = 1	6
VTEC	Feces positive for Vt12eaee		10	0.7 (2.3)		α1 = α2 = 1	2
	Feces positive for Vt12ehxAf		10	1.6 (3.1)		α1 = α2 = 1	3
	Feces positive for eaeehxAg		10	0.7 (2.1)		α1 = α2 = 1	2

^aPFGE, pulsed-field gel electrophoresis; RAPD, random amplified polymorphic DNA; ERIC, enterobacterial repetitive intergenic consensus sequence.

^bBased on expert opinion and entered in the calculations as a known number.

^cThe ovine fecal data set is shown in more detail in Table 3 because it was used to generate a data-based, informative prior distribution (average, 2.9; standard deviation, 1.2).

^dV12, E. coli positive for verotoxin 1,verotoxin 2, or both verotoxins.

^eVt12eae, E. coli positive for either or both of the two verotoxins and intimin (eae).

^fVt12ehxA, E. coli positive for either or both of the verotoxins and hemolysin (ehxA).

^geaeehxA, E. coli positive for intimin and hemolysin (ehxA).

Table 2 provides an overview of the data sets, including the bacterial species, the sample sources, the references for the typing methods, the average number of isolates typed or screened per sample and source, the average number of strains observed per sample, and the expected number of strains detected in the samples based on expert opinion or an independent data set (only for ovine fecal data). The observed within-sample heterogeneity was lowest for non-type-specific E. coli in intestinal samples; on average, there were 1.7 strains (rumen) or 1.3 strains (small intestines) in ovine gastrointestinal samples. The observed within-sample heterogeneity was highest for E. coli and K. pneumoniae in ovine and bovine fecal samples, respectively; an average of three strains were detected among four isolates. Table 2 shows the required numbers of isolates (N), as described below.

Sample size calculations. (i) Combination of prior information and relevant data.

Bayesian statistical inference was used to calculate the number of isolates (N) that must be genotyped to identify all strains present in a future sample with a high (e.g., 95%) probability. Bayesian inference comprises a combination of prior information about parameters in the model and information from relevant data (7). Here, the parameters are the unknown probabilities (θ₁, θ₂,… θ_k) for a sample to contain either exactly one strain, two strains, or up to a maximum of, e.g., six strains (k = 6). The prior information is a summary of what is “known” about θ₁, θ₂,… θ₆ prior to the use of the relevant data. The prior information may be obtained from data that are related to the problem but are not directly applicable (perhaps taken from the literature) or from expert opinion. A prior probability is attached to each possible value of a parameter. Consequently, the prior probability takes the form of a probability distribution. The relevant data are directly applicable to the particular bacterial species in the setting of interest. So, while the prior information contains “soft” information, gathered from related sources, the relevant data represent “hard” information, and both are represented by a statistical model.

Attention is focused on the probability p (derived from θ₁, θ₂,… θ₆) that all strains that are present in a future sample will actually be observed. The result of the calculations is again a distribution, referred to as the posterior (distribution), which offers an up-to-date summary of the information about the parameters. A large sample from the posterior of probability p is generated by a Markov chain Monte Carlo algorithm, as implemented in the WinBUGS package (20). The median for this sample is presented as an estimate for p and the 2.5 and 97.5 percentile points as Bayesian confidence bounds (a 95% credible interval). For each value of N that is specified in the program as a possible future sample size, an estimate and interval for p are derived. The program can be run for a range of potential values for N. An appropriate choice can be made from a table or a plot (for instance, the value for N where the estimate for probability p exceeds 95%).

Choice of priors.

Let there be k different bacterial strains in a sample, where k is assumed to be known. For the probabilities θ₁, θ₂,… θ_k that a sample contains exactly 1, 2, or k strains, we need a prior distribution for positive numbers that add up to 1. The Dirichlet distribution has this property and is a convenient distribution for use as a prior distribution. The form of this distribution depends on the values of its shape parameters (α₁… α_k) that have to be specified.

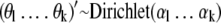(1)

The positive numbers α₁… α_k will be chosen such that equation 1 reasonably reflects the available prior information. A rule of thumb is that prior distribution 1 mimics the information in m = α₁ +… + α_k imaginary samples, with a proportion of the samples with exactly one strain (α_1/m), a proportion (α_1/m) of the samples with exactly two strains (α_2/m), etc.

When little is known a priori, a prior will be chosen that expresses hardly any preference for possible values for θ₁ … . θ_k between 0 and 1. Popular choices for such a relatively uninformative prior are:

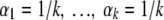(2a)

, and

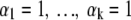(2b)

We show that the impacts of priors 2a and 2b on the results for p are about the same.

Alternatively, when a stronger opinion is voiced about the values of θ₁ … θ_k, based on expert opinion or previously published information, a more informative prior may be chosen. For illustration, the choice of an informative prior for non-type-specific fecal E. coli is discussed below, based on data from a previously conducted experiment, as shown in Table 3. Initially, following the rule of thumb, the α values are chosen to be equal to the counts in Table 3, replacing 0 by 0.5. This is practically equivalent to adding the data of Table 3 to the other relevant data and using prior 2a or 2b. However, when we do not feel quite confident about the data that inform the prior (Table 3), maybe because they relate to somewhat different samples or experimental conditions, we may decide to choose the prior more cautiously. To that end, we multiply the α values by a factor (λ) less than 1; i.e., α_i is replaced by the smaller λα_i, where i = 1… k. The prior expected θ values remain the same (and equal to α₁/m… α_k/m), but the prior distribution is wider, expressing the uncertainty about the relevance of the data that inform the prior (Table 3). The smaller the factor λ that we use, the wider the prior is. The WinBUGS program has simple facilities to see what the prior looks like, so a suitable value for λ may be chosen given the uncertainty about the relevance of the data in Table 3. When there is doubt about the choice of prior, several priors could be used to check their impact on the choice of N in relation to the intended value for p. In Table 2, priors are relatively uninformative, except for the prior for ovine fecal E. coli (data set with n = 50).

TABLE 3.

Data from ovine fecal samples (n = 50) for non-type-specific E. coli: numbers of strain types observed and fractions of the numbers of strain types used to construct an informative prior distribution for the sample size calculations based on the second ovine fecal data set (n = 80) in Table 2^a

No. of strain types observed	Frequency counts of strain types observed
1	6
2	15
3	12
4	11
5	12
6	0.5b

^aThe number of isolates typed per sample was five.

^bSince six different types were not observed in the data set, a value less than 1 was added for the frequency count of observing six different types per sample in order to construct the prior.

(ii) Assumptions in modeling the relevant data.

Below, we discuss the model assumptions in relation to the structure of the data. Similar to the assumption of Altekruse et al. (1), it is assumed that all strains in a sample are equally likely to be observed. The relevant data for the sample size estimate consist of the numbers of strains observed in the samples, as shown in Table 2. Technical details of the model are presented in the Appendix.

The assumption that all strains are equally likely to be observed is relaxed for the special case of two strains or two groups of strains. All strains of interest are placed into one group, while the remaining strains are placed into another group. The data consist of the observed number of isolates with strains that belong to the first group per total number of isolates that are genotyped per sample. In this way, the required future sample size may be calculated for a sample containing heterogeneous populations of pathogens that will be screened, for example, for a rare strain type of interest. Technical details about the model for this special case, including information about the choice of prior distributions, are presented in the Appendix.

Presently, any dependence between data (e.g., repeated measurements for animals) is not taken into account. Technically, it is possible to include a suitable dependence structure in the model of the relevant data. However, this fine-tuning of the model and the WinBUGS program requires intimate knowledge of the data and a fair amount of statistical expertise. It is important to distinguish between an actual analysis of new experimental data, possibly by Bayesian inference, and the present calculation of the required sample size. The sample size calculations will often be based on a simplified model. The present calculations are expected to offer a reasonable indication of the order of magnitude of the required sample size. When the correlation between data is marked, the calculations result in a lower boundary for the required sample size.

RESULTS

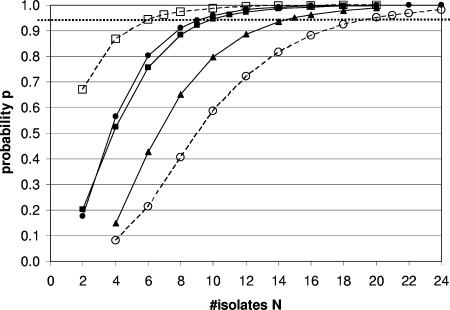
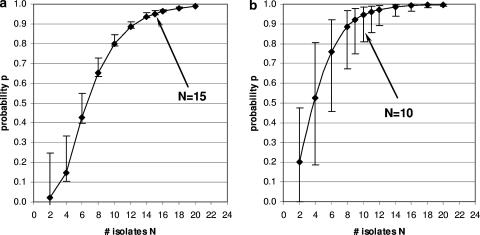
The posterior median of the probability of finding all of the strains that are present in a sample when N isolates per sample are analyzed was calculated for a range of values for N. Figure 1 summarizes the results for L. monocytogenes and S. uberis in soil and for L. monocytogenes, S. uberis, and K. pneumoniae in feces. The numbers of isolates that needed to be typed to find all strains with 95% probability were different for different bacterial species. For example, the number of isolates that needed to be typed to find all strains in a fecal sample with 95% probability varied from approximately 10 for L. monocytogenes or S. uberis to 15 for K. pneumoniae. The differences between bacterial species were even greater for soil samples, where as many as 20 isolates needed to be characterized for S. uberis, while for L. monocytogenes in soil samples characterization of six isolates was sufficient, emphasizing the finding that the required number of isolates varied not only with the bacterial species but also with the sample type. To illustrate the differences in credibility intervals for the probability estimates and a given number of isolates typed per sample, Fig. 2a shows the relatively small credible intervals for K. pneumoniae and Fig. 2b shows the larger credible intervals for the probability estimates for L. monocytogenes.

FIG. 1.

Probability p of finding all strains of a species present in sample when N isolates per sample are characterized. Squares indicate L. monocytogenes, circles indicate S. uberis, and triangles indicate K. pneumoniae. Filled symbols and solid lines indicate fecal samples. Open symbols and dashed lines indicate soil samples. Cut-offs with the horizontal dotted line that marks the 95% probability p yield the numbers of required isolates (N) (e.g., N is about 6 for L. monocytogenes in soil □).

FIG. 2.

K. pneumoniae (a) and L. monocytogenes (b) from bovine fecal samples have different widths of the 95% credible interval (indicated by errors bars) and result in different sample sizes for the 95% probability of typing all strains present in the samples.

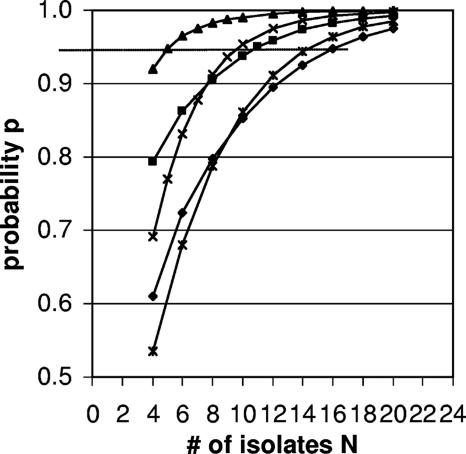
For ovine E. coli, the number of isolates that need to be characterized to identify all strains in the sample with 95% probability is expected to depend on the gastrointestinal origin of the sample and on the prior distribution that is used in Bayesian analysis (Fig. 3 and Table 2). When the relatively uninformative prior 1b was used, the number of isolates needed ranged from 5 for samples from the small intestine and 10 and 11 for samples from the large intestine and rumen, respectively, to 16 for fecal samples. The alternative relatively uninformative prior 1c yielded virtually the same results. When an informative prior distribution that was derived from an independent data set from an independent study was used (50 ovine fecal samples [Table 1]), the number of isolates required to identify all strains in a fecal sample with 95% probability was reduced from 16 to 14 (Fig. 3).

FIG. 3.

Probability p of finding all strains of VTEC and non-type-specific E. coli in small intestine (triangles), large intestine (multiplication signs), rumen (squares), and feces (diamonds) samples when N isolates per sample are typed. The dotted horizontal line indicates 95% probability. The triangles, multiplication signs, squares, and diamonds show posterior probability distributions based on expert opinion and a uniform prior. The asterisks show distributions based on an informative prior for ovine fecal E. coli derived from the analysis of an independent fecal data set (n = 50 [Table 1]).

Given the unequal relative frequencies of E. coli coding for selected virulence factors versus all other non-type-specific E. coli, the number of isolates per sample that have to be tested in order to be 95% confident that E. coli carrying this selection of virulence markers is found in the bovine fecal samples can be calculated. Six isolates per sample need to be screened to be 95% confident that E. coli coding for verotoxin 1, verotoxin 2, or both verotoxins is found. Two isolates per sample need to be tested to be 95% confident that E. coli that carries either or both of the two verotoxins in combination with intimin is detected. Three isolates need to be typed to achieve this confidence level for E. coli with either of the verotoxins in combination with hemolysin, and two isolates need to be typed to detect E. coli coding for intimin in combination with hemolysin. The calculated sample sizes (N) per data set are shown in Table 2.

DISCUSSION

The estimated number of isolates to be typed is meant as a minimum detection limit for finding all types of isolates present with a given confidence for different bacterial species and different sources of samples. Such knowledge is essential when workers are trying to detect or, even more difficult, to rule out certain substrates as possible sources of strains of interest. The importance of characterization of multiple isolates when heterogeneous populations of pathogens are studied has been described previously (1, 19), but the current study illustrates how the concept plays out when workers examine a single bacterial species in samples with different origins or multiple bacterial species in samples with only one origin. For K. pneumoniae, strain heterogeneity is limited in milk and soil samples but high in fecal samples (one, one, and four strains per sample, respectively) (16). For S. uberis, strain heterogeneity is limited in milk and fecal samples but high in soil samples (1, 1.5, and 4 strains per sample, respectively) (23). To characterize bacterial heterogeneity in soil samples, the number of S. uberis isolates that needs to be typed is almost four times as high as the number of L. monocytogenes isolates that needs to be typed (Fig. 1).

We provide a single program in WinBUGS code that enables the user to perform all the required calculations together. In contrast to previous publications (1, 19), there is no need to resort to additional programs to, e.g., evaluate some probabilities relevant to the calculations by simulation as model input. The WinBUGS package (20) is freely available on the internet (http://www.mrc-bsu.cam.ac.uk/bugs). The WinBUGS programs, as used for the current sample size calculations, are available from D. Döpfer, together with instructions. A microbiologist provides microbial typing data and expert opinion about how many types are expected to exist in the data. The informed user of the WinBUGS program, for example a microbiologist or a statistician, has to specify prior information about model parameters based on the expert opinion or independent data sets and information about the uncertainty about this prior information. The choice of prior distributions is discussed in some detail. The relatively flat priors (priors 1b and 1c) can be used routinely, when the user has little prior information or intends to include little prior information in addition to the data that are considered directly relevant for the bacterial species and particular study. The statistician informs the microbiologist with regard to the number of isolates per sample that needs to be analyzed, based on the microbiologist's research question and expert opinion, as well as relevant data.

The process of updating the information, as illustrated for the informative prior for ovine fecal E. coli with information derived from an independent pilot data set, is iterative, and sample size information can be improved with each study that is undertaken. Updating information through consecutive studies lies at the core of Bayesian statistical inference (2, 7).

Bayesian statistical approaches are often criticized for employing expert opinion to generate prior distributions. Calculations in this study show that with the same priors derived from expert opinion (e.g., L. monocytogenes in soil versus fecal samples), different posterior distributions for the probability p of detecting all strains present can be obtained (10 versus 6 strains [Table 2]). This demonstrates that even data sets of modest size (10 samples for L. monocytogenes [Table 1]) contain information that is extracted by the Bayesian inference and reflected by the posterior distributions of p. Credible intervals for p for different data sets may vary in width, as demonstrated for K. pneumoniae versus L. monocytogenes in fecal samples (Fig. 2a and b). This difference in credible intervals demonstrates that the posterior critically depends on the amount and heterogeneity of the data. The “molecular typing walk” through the ovine gastrointestinal tract illustrates how different the numbers of E. coli isolates necessary for typing can be, where the rumen and large intestines have higher values than the small intestines. The presence of E. coli strains with different relative frequencies (e.g., specific virulotypes versus all other strains) can be detected at a certain level of confidence, as demonstrated using the bovine fecal E. coli isolates.

It is often assumed that all bacterial strains that are present in a sample are equally likely to be isolated. This may not always be true. For example, potentially pathogenic VTEC is known to comprise about 1% of all E. coli in the feces of ruminants (15). The number of isolates that needs to be tested to find at least one isolate of a given type, if it is present in a less-than-average percentage of all cases, may be far higher (14). This is particularly relevant when selective or indicator media for detection of the strain of interest are not available For example, in one of our laboratories, a real-time PCR test for detection of VTEC in bulk tank milk is used. No selective or indicator media are available for non-O157:H7 VTEC, and the high heterogeneity of E. coli strains in bulk tank milk turns finding a VTEC isolate into the proverbial looking for a needle in a haystack. In the analysis presented here, the assumption that strains are equally likely to be present in a sample is relaxed for strains that are collected in two groups (for example, different groups of genotypes, virulotypes, or other typing strategies, such as serotyping). We are presently developing an extension of the model where the assumption is relaxed further. The present study is meant to further enhance the awareness about the numbers of isolates that need to be typed in a sample for heterogeneous populations of pathogens, as initiated by Singer et al. (19) and Altekruse et al. (1).

Another improvement in the calculation of numbers of isolates that need to be typed may be to incorporate hierarchy in the data (e.g., data from field studies comprising repeated measurements per farm, animal, food processing plant, or site). To this end, the current WinBUGS program needs to be fine-tuned, which requires considerable statistical expertise and goes beyond routine use of the present WinBUGS programs.

Independent of the typing method, it is likely that there will be heterogeneity of isolates in many sample types and surveys, which makes typing of multiple isolates per sample necessary so that information is not lost. Variation across niches, species, and time implies that sample size calculations benefit from a pilot study before large-scale molecular typing studies are performed. The worst outcome of a “blind” typing and sampling strategy for heterogeneous populations of pathogens would be a failure to detect a zoonotic or bioterrorism hazard. Given the progress of automated typing of microorganisms, it is not unthinkable that multiple isolates per sample will be typed in the near future.

APPENDIX

Details of the statistical calculations: model with more than two strains.

The relevant data are the numbers of strains that are observed in different samples as determined by molecular typing. The probability of observing j strains is more easily expressed when we know that exactly i strains are present in a sample. This probability is indicated by P_n(j|i), where the index n expresses the dependence on the number of n isolates that are typed in a sample and can be obtained from the study of Johnson and Kotz (10):

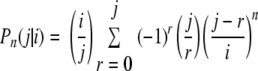The probability of observing j strains, regardless of the value of I, is:

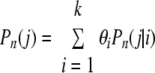These expressions are derived by assuming that all strains in a sample are equally likely to be observed. Note that the relevant data may comprise data for samples in which different numbers of isolates are genotyped. The probability of observing all strains that are present in a sample, for a number of isolates (N) that are to be typed for a future sample, is:

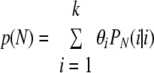This probability is introduced as an additional derived parameter in the WinBUGS program.

Details of the statistical calculations: model with two (groups of) strains.

Let all strains of interest be placed in one group, referred to as type A, while the remaining strains are placed in another group, referred to as type B. Types A and B are now the only types in the analysis. Let x be the number of isolates of type A that are observed in a sample where n isolates are genotyped (x = 0… n). Let θ₁, θ₂, and θ₃ be the probabilities that a random sample contains only type A isolates, only type B isolates (i.e., no type A isolates), or both type A and B isolates, coded by t = 1, t = 2, and t = 3, respectively. Depending on the type of sample, t = 1, t = 2, and t = 3, and x follow a binomial distribution with total n and probability 1, 0, and φ, respectively. Note that we no longer assume that all strains in a sample have an equal probability of being observed, since the probability φ is not restricted to be equal to 0.5. The probability of detecting at least one isolate of each type that is present in the sample, when N isolates are genotyped, is:

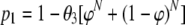Alternatively, we could focus on the probability (p₂) of detecting at least one isolate of type A, when type A is present in the sample:

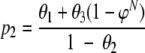For the θ probabilities we use a Dirichlet prior distribution, as described previously, and for probability φ we use a beta prior distribution. Actually, the beta distribution for φ is the same as the Dirichlet distribution for φ and (1 − φ) for k = 2. Prior 2b yields the uniform distribution for φ for the interval from 0 to 1.