Risk-Adaptive Optimization: Selective boosting of high-risk tumor subvolumes

Abstract

Background and purpose

A tumor subvolume-based, risk-adaptive optimization strategy is presented.

Methods and materials

Risk-adaptive optimization employs a biological objective function instead of an objective function based on physical dose constraints. Using this biological objective function, TCP is maximized for different tumor risk regions while at the same time minimizing NTCP for organs at risk (OAR). The feasibility of risk-adaptive optimization was investigated for a variety of tumor subvolume geometries, risk-levels, and slopes of the TCP curve. Furthermore, the impact of a correlation parameter, δ, between TCP and NTCP on risk-adaptive optimization was investigated.

Results

Employing risk-adaptive optimization, it is possible in a prostate cancer model to increase EUD by up to 35.4 Gy in tumor subvolumes having the highest risk classification without increasing predicted normal tissue complications in organs at risk. For all tumor subvolume geometries investigated, we found that the EUD to high-risk tumor subvolumes could be increased significantly without increasing normal tissue complications above those expected from a treatment plan aiming for uniform dose coverage of the PTV. We furthermore found that the tumor subvolume with the highest risk classification had the largest influence on the design of the risk-adaptive dose distribution. The parameter δ had little effect on risk-adaptive optimization. However, the clinical parameters D₅₀ and γ₅₀ that represent the risk classification of subtumor volumes had the largest impact on risk-adaptive optimization.

Conclusions

On the whole, risk-adaptive optimization yields heterogeneous dose distributions that match the risk level distribution of different subvolumes within the tumor volume.

I. INTRODUCTION

Recent technological developments have introduced impressive changes in the field of radiation therapy (RT). For instance, the advent of intensity-modulated radiation therapy (IMRT) permits the increased conformality of the dose to the tumor volume and avoidance of OAR. A variety of different image-guided IMRT (IG-IMRT) techniques have been proposed resulting in minimizing geometric uncertainties caused by organ motion/deformation of the target and OAR and day-to-day set-up variation. Therefore, the uniformity in dose-distribution on targets starts to lose its rationale that was described by Webb and Nahum as “the general rule in radiotherapy that only small inhomogeneities in dose can be tolerated… Chances are higher [in conformal therapy] that a shift in patient position could bring some region of the target volume outside the high-dose volume” [1]. In addition, further advances in physiological imaging will provide information about the tumor at the cellular and functional level, and therefore lead to a better assessment of spread, cellular density, variation of radiosensitivity of clonogenic tumor cells, and information on the distribution of radiation sensitive functional subunits (FSU) in normal tissues [2, 3, 4, 5, 6]. Physiological imaging of tumors will allow selective boosting of tumor subvolumes as proposed by a number of investigators [7, 8, 9, 10]. The therapeutic benefit of boosting has been postulated to result in increased survival rates and reduced local reoccurrence rates. Thames et al. [11] found that a 10% to 20% boost dose to target volumes could result in a measurable increase in survival for a cohort of 50 to 200 patients having radioresistant primary tumors. The EORTC boost trial [12] confirmed this by showing a significant increase in locoregional control in the boost track. In the boost group, 109 local recurrences were observed in a total of 2661 patients while in the standard-treatment group 182 local recurrences were observed in a total of 2657 patients. However, to prevent one local recurrence, 34 patients needed to be boosted. This invokes the therapeutic problem that if all patients would be treated with the boost technique a number of them would incur added side effects from the additional dose even though they were already destined for local control without boosting.

The intrinsic deficiency of whole boost therapy is that the boost doses used are based on previous experience rather than on patient-specific data. On the other hand, ‘selective’ boosting would only be used for patients that have tumor-subvolumes at risk for local recurrence, which are identified using advanced physiological imaging techniques [7, 8, 9, 10]. Tomé and Fowler found from modeling that selective boosting of tumor subvolumes results in an increase in tumor control probability (TCP) up from 50 % to 70 % if 60% to 80% of the tumor can be boosted to 20%–30% above the minimal peripheral prescription dose [7]. While there is still a need for clinical verification that novel physiological imaging techniques indeed show the spatial location of hypoxic or radio resistant volumes and whether patients indeed benefit if these tumor subvolumes identified using these imaging techniques are selectively boosted to higher doses, it has been hypothesized that for tumor sites where hypoxia impacts on overall survival such as head and neck (H&N), selective boosting might provide a benefit [3].

The question therefore arises: How can we genuinely use selective-boosting in high risk tumor subvolumes while avoiding injury of radiosensitive normal-tissues? In an effort to balance tumor control and normal tissue complications, Brahme [13] explored the use of biological inverse-treatment-plan-optimization. Biologically optimized treatment planning has the potential to strike the right balance between cure and complications. This results from the fact that radiobiological model-based optimization enables one to include the volume dependence of organs to radiation injury as well as their internal structural organization in terms of FSU. Moreover, biological optimization allows one to include the possible physiological characteristics of different tumor subvolumes that are currently not included in the treatment planning process. In order to explore the feasibility of optimization based on the characteristics of tumor-subvolumes, we have classified them into three categories: geometry, risk-grade, and steepness of their dose-response curve. A novel risk-adaptive optimization strategy is proposed, and a study has been carried out using a prostate cancer model in which dose distributions are optimized based on possible risk characteristics for local recurrence in tumor subvolumes. Additionally, we have investigated the impact of correlation of TCP and NTCP on the risk-adaptive optimization process when combined into a biological objective function, which we denote by UTCP_δ. Apart from the pioneering efforts of Ågren et al. [14] to evaluate the correlation-parameter, δ, from patient data, its impact on optimization has not been further explored.

Therefore, it is the objective of this study to explore the feasibility of risk-adaptive optimization using phenomenological TCP and NTCP models whose input parameters can be obtained from clinical data and the impact of the correlation parameter, δ, on risk adaptive optimization.

II. METHODS AND MATERIALS

Risk-Adaptive Optimization in IMRT Treatment Planning

A optimization-framework using TCP and NTCP which allows the optimization of IMRT treatment plans based on the risk for tumor recurrence in different subvolumes within the GTV while respecting the normal tissue complication probabilities of the organs at risk (OAR) has been constructed and implemented. The ADAC Pinnacle^™ treatment planning system (TPS), version 7.9, was used to calculate the dose distribution and the dose-volume-histograms (DVH) for a prostate cancer model resulting from a risk-adaptive optimization that had been built as a Plugin for the Pinnacle TPS. An equiangular beam arrangement consisting of seven coplanar fields has been employed for all investigated risk-adaptive optimizations. The same dose grid of 0.4 cm × 0.4cm × 0.4 cm was used for all cases. The prescribed dose to the low risk volume was 64 Gy to 95% of the planning target volume (PTV) in 32 fractions of 2 Gy. In order to investigate the dose-behavior induced by risk-adaptive optimization, no variations in beam geometry or prescription to the low risk volume were made. Hence, we have employed a typical framework for prostate IMRT apart from the fact that we have used risk-adaptive optimization instead of physical dose optimization. Riskadaptive optimization employs a biological objective function based on TCP and NTCP instead of an objective function based on physical dose constraints. Using this biological objective function, one maximizes the TCP values for the different tumor risk regions while at the same time minimizing the NTCP values for OAR. This was achieved by maximizing the biological objective function UTCP_δ, which is given by the following expression:

$${\mathit{UTCP}}_{\delta }=(\mathit{TCP}-\mathit{NTCP})+\delta \{\mathit{NTCP}(1-\mathit{TCP})\}$$ (1)

where δ is the estimated fraction of patients for which tumor and normal tissue response are statistically independent (0.0 ≤ δ ≤ 1.0 ) [13]. For instance, given a value of 0.2 for the correlation-parameter, δ, dictates that for 20 % of patients tumor control and incidence of normal tissue complication are uncorrelated while the remaining 80% of patients may suffer a normal tissue complication in the attempt to achieve local tumor control. According to Ågren and colleagues [14], the fraction δ of patients is defined as “a statistically independent subpopulation”. This definition implies that for a delta value δ = 0, the genetic radio-characteristics (susceptibility/resistance) to radiation are the same for both tumor and normal tissue, i.e. all patients may suffer normal tissue complications in the attempt to achieve local tumor control.

Subvolume-based TCP Model

In this paper, we have chosen to work with a phenomenological TCP model that is given by the logistic expression:

$$\mathit{TCP}(D)=\frac{1}{1+{\left(\frac{D_{50}}{D}\right)}^{4{\gamma }_{50}}}$$ (2)

where the two parameters D₅₀ and γ₅₀ are determined from clinical data. D₅₀ is the dose which yields a tumor-control probability of 50%. This model applies to tumors that receive a uniform dose, D. We assume that D₅₀ and γ₅₀ can be determined for different physiological tumor types using either biopsies or functional imaging techniques. We have classified these physiological tumor types as low, intermediate, high, and very high risk for resistance to radiotherapy (cf. Table 2). Now, if we think of our tumor or target as being composed of R different risk subvolumes each receiving a uniform dose D_j, then the overall expected TCP will be the product of the expected TCP for the individual risk regions:

$$\mathit{TCP}=\prod _{j=1}^R{[\mathit{TCP}(D_j)]}^{{\nu }_j}$$ (3)

where ν_j is the fractional volume of the j^th-subvolume of the tumor (cf. appendix for the proof) and R denotes the total number of tumor subvolumes. Since tumors are the ultimate parallel structures, the overall tumor is controlled if and only if all of the tumor subvolumes are controlled, i.e. if every single potentially malignant cell is damaged to such an extent that it cannot continue to proliferate [15]. In what follows, let us now assume that we have in subvolume j an inhomogeneous dose distribution, ${\left\{D_i^j,{\nu }_i^j\right\}}_{i=1}^k$ where ${\nu }_i^j$ is the fractional volume of subvolume j receiving the constant total dose, $D_i^j$, then the expected TCP for subvolume j is given by (cf. appendix for the proof):

$${\mathit{TCP}}_j\left(\left\{D_i^j,{\nu }_i^j\right\}\right)=\prod _{i=1}^k{\left[\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{4{\gamma }_{50}^j}}\right]}^{{\nu }_i^j},\text{where}\sum _{i=1}^k{\nu }_i^j=1$$ (4)

where $D_i^j$ is constant across the tumor voxels having a fractional volume of ${\nu }_i^j$. In equation (4), we have made the generalization that each of the R-subvolumes may have a different $D_{50}^j$ and ${\gamma }_{50}^j$ which are based on its physiological tumor risk make-up. This approach assumes of course that we have a method to estimate the different $D_{50}^j$ and ${\gamma }_{50}^j$ either from population based clinical data or from individual tumor based assessments particular to each patient. Therefore, the overall tumor subvolume based TCP is given by (cf. appendix for the proof):

$$\mathit{TCP}(\{D\})=\prod _{j=1}^R{\left[{\mathit{TCP}}_j(\{D_i^j,{\nu }_i^j\})\right]}^{{\nu }_j}=\prod _{j=1}^R{\left(\prod _{i=1}^k{\left[\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{4{\gamma }_{50}^j}}\right]}^{{\nu }_i^j}\right)}^{{\nu }_j}$$ (5)

where {D} denotes the inhomogeneous dose distribution in the entire tumor. The detailed derivations of this subvolume-based TCP and the gradient of the TCP function needed for risk-adaptive optimization using inverse planning are given in the appendix. To summarize our expression for the overall subvolume-based TCP of a tumor, we hypothesize that each of the R-tumor-subvolumes has different $D_{50}^j$ and ${\gamma }_{50}^j$ values that are based on the physiological tumor makeup of the tumor-subvolume and that these values can be obtained from clinical data. Therefore, the subvolume-based TCP model presented in equation (5) represents one possible way of formulating a phenomenological TCP function for personalized risk-adapted radiation therapy.

Table 2.

Arrangements of D₅₀ and the steepness of dose-response curve (γ₅₀).

Case		A high risk sub-tumor region (Nodule)		A remainder region of PTV (rPTV)
TCD50-Combinations	H+–L	Very High risk	[D50 = 84.5Gy]	Low risk	[D50 =54.5Gy]
	H+–M	Very High risk	[D50 =84.5Gy]	Intermediate risk	[D50 =64.5Gy]
	H–M	High risk	[D50 =74.5Gy]	Intermediate risk	[D50 =64.5Gy]
	M–M	Intermediate risk	[D50 =64.5Gy]	Intermediate risk	[D50 =64.5Gy]
Dose-response slope-combinations	2–2	A low slope	[γ50=2]
	5–2	A intermediate slope	[γ50=51	A low slope	[γ50=2]
	8–2	A steep slope	[γ50=8]
	2–5	A low slope	[γ50=2]
	5–5	A intermediate slope	[γ50=5]	A intermediate slope	[γ50=5]
	8–5	A steep slope	[γ50=8]
	2–8	A low slope	[γ50=2]
	5–8	A intermediate slope	[γ50=5]	A steep slope	[γ50=8]
	8–8	A steep slope	[γ50=8]

Voxel-based NTCP Model

Again for simplicity, we have chosen to work with a phenomenological NTCP model given by the logistic expression. In order to employ the clinical data fitted to the Lyman-Kutcher-Burman (LKB) model, γ₅₀ was simply replaced by $\frac{1}{\sqrt{2\pi }m}$. This can be straightforwardly derived from the LKB model by simply evaluating the dose gradient at D = D₅₀. We have assumed no volume effect for individual normal tissue voxels so that our phenomenological NTCP is given by:

$$\mathit{NTCP}=\frac{1}{1+{\left(\frac{D_{50}}{D}\right)}^{\frac{4}{\sqrt{2\pi }m}}}$$ (6)

where D₅₀ and m are again determined from clinical data fitted using the LKB model. Of course, it is well known that with this substitution for γ ₅₀ the logistic model becomes equivalent to the LKB model with no volume effect (i.e. n = 0) [16]. Intuitively, this equivalence is clear since we have simply reparametrized one cumulative probability function to match another. Given Q different OAR, the overall NTCP is determined using Bayesian statistics and is expressed as the product of the expected NTCP for the individual OAR:

$$\mathit{NTCP}=1-\prod _{j=1}^Q\left[1-\mathit{NTCP}(\{D_i^j,{\nu }_i^j\})\right]$$ (7)

where Q refers to the number of OAR. In our formulation of NTCP, all complications have an equal likelihood of occurrence if their probabilities to manifest are equal. As a result, the overall NTCP is governed by the most sensitive OAR rather than the lowest value of NTCP. Equation (7) also avoids the problem of zero overall NTCP if one of the OAR has zero NTCP. Given a number of ${\left\{OA{R}_j\right\}}_{j=1}^Q$, let us now assume that we have in OAR_j the inhomogenous dose distribution, ${\left\{D_i^j,{\nu }_i^j\right\}}_{i=1}^l$, where ${\nu }_i^j$ is the fractional volume of OAR_j receiving the constant total dose, $D_i^j$, then the expected NTCP for OAR_j is given by (cf. the appendix for the proof):

$$\mathit{NTCP}\left(\left\{D_i^j,{\nu }_i^j\right\}\right)=1-\prod _{i=1}^l{\left(1-\mathit{NTCP}(D_i^j)\right)}^{{\nu }_i^j},\text{where}\mathit{NTCP}(D_i^j)=\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{\frac{4}{\sqrt{2\pi }m}}}\text{and}\sum _{i=1}^l{\nu }_i^j=1$$ (8)

Thus, the overall voxel-based NTCP for Q organs at risk is given by:

$$\mathit{NTCP}\left(\left\{D\right\}\right)=1-\prod _{j=1}^Q\left[1-\left(1-\prod _{i=1}^l{\left(1-\mathit{NTCP}(D_i^j)\right)}^{{\nu }_i^j}\right)\right],\text{where}\mathit{NTCP}(D_i^j)=\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{\frac{4}{\sqrt{2\pi }m}}}\text{and}\sum _{i=1}^l{\nu }_i^j=1$$ (9)

where {D} denotes the inhomogenous dose distribution in the entire irradiated volume. The derivation of the gradient calculation for NTCP that is required to carry out inverse treatment planning is given in the appendix.

The Biological Objective Function UTCP_δ

The present analysis is based on the P₊ model proposed by Källman et al. [17] who have represented P₊ as P₊ = P_B−P_B∩I. Here, P_B denotes the probability of benefit (TCP), and P_B∩I refers the probability of having both tumor control and normal tissue complications. There are two limiting cases for which P₊ can be expressed in a simple equation in terms of TCP and NTCP. The first limiting case assumes that each cure leads to a complication and therefore P₊ is obtained as the difference of TCP and NTCP. Hence,

$${\mathit{UTCP}}_0=\mathit{TCP}(\{D\})-\mathit{NTCP}(\{D\})$$ (10)

In the second limiting case it is assumed that tumor control probability is independent of normal tissue complication probability, and P₊ in this case is also known as uncomplicated tumor control probability:

$${\mathit{UTCP}}_1=\mathit{TCP}(\{D\})[1-\mathit{NTCP}(\left\{D\right\})]$$ (11)

Using equations (5) and (7), the voxel-based UTCP₁ is given by:

$${\mathit{UTCP}}_1=\prod _{j=1}^R{\left[\mathit{TCP}\left(\left\{D_i^j,{\nu }_i^j\right\}\right)\right]}^{{\nu }_j}\times \left[1-\left\{1-\prod _{j=1}^Q\left[1-\mathit{NTCP}\left(\left\{D_i^j,{\nu }_i^j\right\}\right)\right]\right\}\right]$$ (12)

A more general expression, UTCP_δ, can be obtained by linear combination of these two limiting cases:

$${\mathit{UTCP}}_{\delta }=\mathit{TCP}(\{D\})-\mathit{NTCP}(\{D\})+\delta ·\mathit{NTCP}(\{D\})\left[1-\mathit{TCP}(\{D\})\right]$$ (13)

For small delta-values, UTCP_δ can be interpreted as follows: a given absolute increase/decrease in the chance for local tumor control on one side will be balanced with a similar decrease/increase in risk for complications on the other. A derivation of the gradient of UTCP₁ and UTCP_δ can be found in the appendix.

Biological parameters employed in our risk-adaptive optimization strategy are shown in Table 1. Rancati and colleagues explored the fit of different NTCP models such as the LKB model and the logistic model to the clinical data of 547 prostate cancer patients. We have chosen to work with the D₅₀ and m for the LKB model for late-rectalbleeding determined by Rancati et al. [18]. For the bladder and the unspecified normalpelvic tissue, we have used data given by Emami et al. [19]. Since most of the unspecified normal-pelvic tissue close to the prostate consists of the small and large bowels, we have employed the Emami data for the small intestine and colon in the estimation of NTCP for the unspecified normal-pelvic tissue. Boersma and colleagues [20] have investigated whether DVH parameters can be used to identify risk groups for developing late GI and GU complications. They have commented that the LKB NTCP model cannot be expected to yield reliable estimates for the incidence of GU complications since the relative bladder wall dose volumes used in the estimation of these normal tissue complication probabilities depend on the bladder filling. In spite of emerging new clinical data for rectal complications [18, 20], xerostomia [21], and radiation induced liver disease [22] that were fitted to the LKB model, the radiation tolerance data for the bladder published by Emami et al. in 1991 has not been updated. In what follows we will make use of the following risk tumor subvolume risk classifications: Low (D₅₀ = 54.5 Gy), intermediate (D₅₀ = 64.5 Gy), high (D₅₀ = 74.5 Gy), and very high (D₅₀ = 84.5 Gy). These estimates of D₅₀ have been motivated by the recently published data of Levegrün et. al. [23].

Table 1.

TCP and NTCP model parameters in the Risk-Adaptive Optimization for prostate cancer.

Structure	D50 [Gy]	γ50 or m
Rectum	81.9	m = 0.19
Bladder	80.0	m = 0.11
Unspecific Normal tissue	55.0	m = 0.13
PTV (low risk)	54.5	γ50 = 2~8
PTV(intermediate risk)	64.5	γ50 = 2~8
PTV(high risk)	74.5	γ50 = 2~8
PTV(very high risk)	84.5	γ50 = 2~8

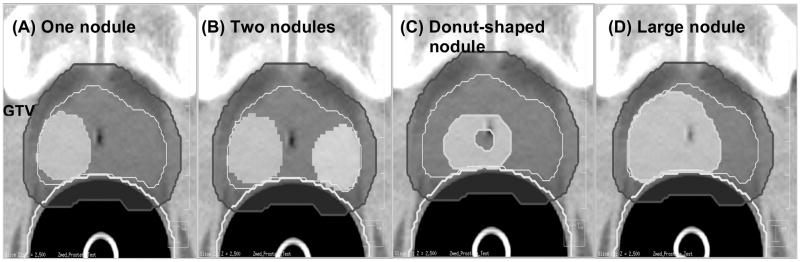
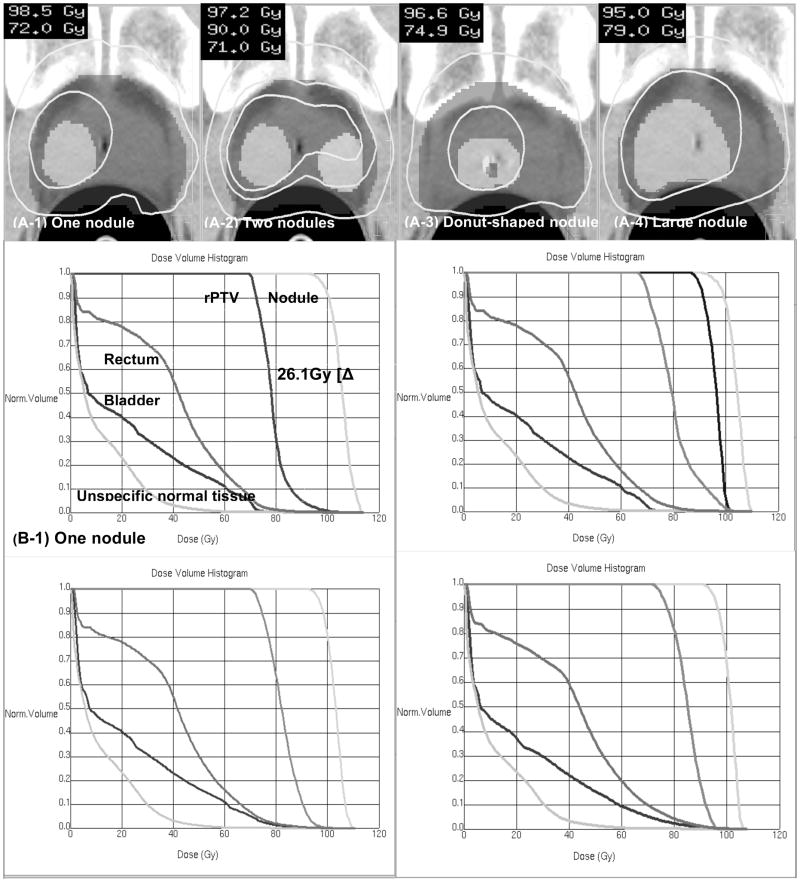
A variety of nodule geometries were constructed to investigate the feasibility of risk-adaptive optimization. In total, four different nodule-geometries were constructed: (a) one nodule that had a volume of 10.3 % of the PTV (93.4 cm³), (b) two nodules that consist of a volume of 10.3 % and 5.4 % of the PTV, respectively (c) donut-shaped nodule in which the lower-risk PTV region is embedded into the high-risk nodule (16.3 % volume of PTV), and (d) a large nodule whose volume is 31.8 % of the PTV. These four nodule geometries are shown in Figure 1. For each of these geometries, a series of risk-adaptive optimizations were then performed by incrementing the value of δ from 0 to 1 using a step size of 0.1 to study the impact of δ on risk adaptive optimization. For this part of our study the following risk characteristics were chosen for all geometries: A very high-risk (D₅₀ = 84.5 Gy) for the nodules and an intermediate-risk (D₅₀ = 64.5 Gy) for the remaining PTV (rPTV) exclusive of nodules, and a steep γ₅₀ = 8.0 for both nodule and rPTV. For a particular patient, the individual γ₅₀ is likely to be steeper than that for a population of patients with similar tumors and therefore a steep γ₅₀ was postulated.

Figure 1.

The high-risk nodule set-up used to evaluate the δ dependency on the nodule geometry from left to right: (a) one-nodule case (b) two-nodule case (c) donut-shaped-nodule case (d) big-nodule case

In order to study the impact of nodule risk on the boost dose that can be achieved in the nodule using risk-adaptive optimization we have constructed 4 different risk classes. For tumor subvolumes (nodules) that are assumed to exhibit risk attributes such as rapid proliferation, rapid metabolism, or hypoxia, risk was classified into 3 classes: intermediate (D₅₀ = 64.5 Gy), high (D₅₀ = 74.5 Gy), and very high (D₅₀ = 84.5 Gy). The rPTV was assumed to have a low risk (D₅₀ = 54.5 Gy) or an intermediate risk. Using these risk arrangements, four scenarios were constructed: (1) a very highrisk nodule and a low-risk rPTV (H₊ – L case), (2) a very high-risk nodule and an intermediate-risk rPTV (H₊ – M case), (3) a high-risk nodule and an intermediate-risk rPTV (H – M case) and (4) an intermediate-risk for both a nodule and rPTV (M – M case) (cf. Table 2). All four cases were repeatedly optimized using a steep γ₅₀ = 8.0 for both the nodule and the rPTV, and the value of δ was incremented from 0.0 to 1.0 employing a step size of 0.5.

To evaluate the impact of different steepness of the dose-response curves in different tumor subvolumes on the risk-adaptive optimization, three different slopes of the dose response curve were considered: (1) a flat (γ₅₀ = 2.0), (2) an intermediate (γ₅₀ = 5.0), and (3) a steep (γ₅₀ = 8.0) slope. For the H₊-M risk arrangement, these three slope values were combined to yield the nine cases of different slope settings in the nodule and the rPTV shown in Table 2. These cases were repeatedly optimized incrementing the value of δ from 0.0 to 1.0 employing a step size of 0.5.

Hence, 17 different nodule scenarios were explored to examine the feasibility of the risk-adaptive optimization in inverse planning. 77 risk-adaptive optimizations were carried out to obtain an understanding of the impact of the parameter δ on risk-adaptive optimization.

III. RESULTS

In order to quantify the impact of the δ value on risk-adaptive optimization, we have calculated the equivalent uniform dose (EUD) for target structures, determined the %-volume of the rectal wall receiving a dose above 50Gy, 60Gy, and 70Gy, and determined the maximum dose received by the bladder. Table 3 summarizes the results of all 77 optimizations.

Table 3.

Average doses [EUD] for TVs, percent volume receiving 50 Gy, 60 Gy, and 70 Gy for the rectum, and maximum doses for the bladder.

Case		Nodule EUD[Gy]	rPTV EUD[Gy]	Rectum [% Volume receiving]			Bladder Max.[Gy]
				[50 Gy]	[60 Gy]	[70 Gy]
TCD50-Combinations	H+ - L case	104.6	69.2	31.0%	15.1%	3.9%	87.4
	H+ - M case	100.7	74.6	30.7%	16.7%	6.5%	83.4
	H - M case	89.9	74.8	35.4%	19.9%	8.9%	77.9
	M - M case	81.2	76.2	29.6%	16.3%	6.7%	78.1
	Average	94.1	73.7	31.7%	17.0%	6.5%	81.7
Dose-response slope-combinations	2 - 8 case	103.9	75.9	38.0%	21.6%	9.0%	85.0
	5-8 case	103.7	74.6	31.6%	17.1%	6.9%	84.2
	8 - 8 case	100.6	74.6	30.8%	16.6%	6.5%	83.4
	2-5 case	104.0	77.6	39.7%	22.9%	10.6%	85.9
	5-5 case	103.7	76.3	33.2%	18.1%	8.0%	84.3
	8-5 case	100.6	76.3	32.2%	17.5%	7.7%	83.3
	2 - 2 case	108.8	75.8	39.0%	21.9%	10.2%	88.3
	5-2 case	104.0	78.2	35.7%	19.4%	8.6%	85.6
	8-2 case	100.5	77.5	34.1%	18.1%	7.4%	83.5
	Average	103.3	76.3	34.9%	19.2%	8.3%	84.8
Nodule Geometry	1 nodule case	100.7	74.6	30.7%	16.7%	6.5%	83.4
	2 nodules case	99.0 92.8	72.8	31.8%	17.2%	7.0%	80.6
	Donut-shaped nodule case	99.4	76.5	30.0%	15.8%	6.6%	95.8
	Large nodule case	97.6	78.8	35.3%	19.6%	9.7%	95.7
	Average	97.9	75.7	31.96%	17.31%	7.44%	88.9
	Average	99.4	75.5	33.3%	18.1%	7.6%	85.1

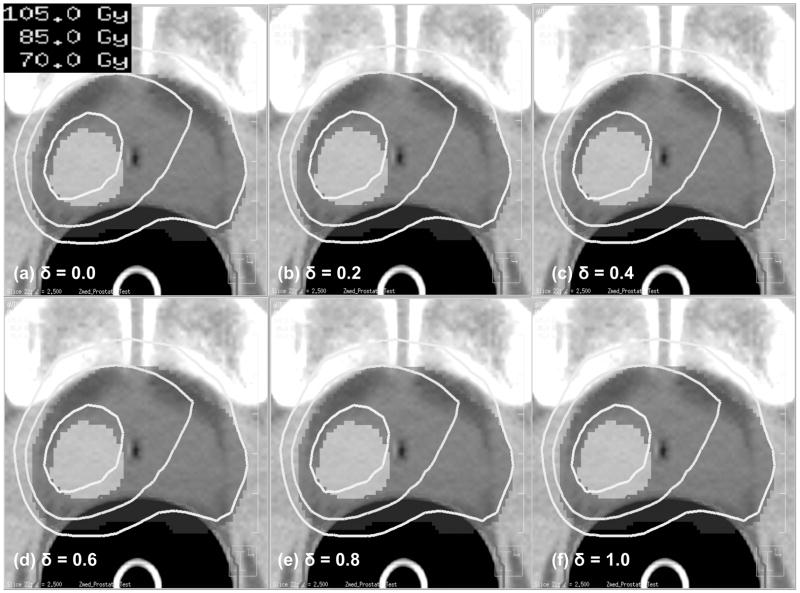
The δ value was found to have little influence on risk-adaptive optimization. This result is illustrated in Figure 2 which shows resulting isodose distributions as a function of the δ -value. From left to right, successive diagrams show the optimization results for six different δ -values (0.0, 0.2, 0.4, 0.6, 0.8 and 1.0). As can be seen from Figure 2, there are no significant differences among these six risk-adaptive IMRT plans besides slight variations in the maximum dose induced through the optimization process — std. dev 0.08 Gy.

Figure 2.

Isodose distributions obtained using Risk-Adaptive Optimization for a range of δ values from 0.0 to 1.0.

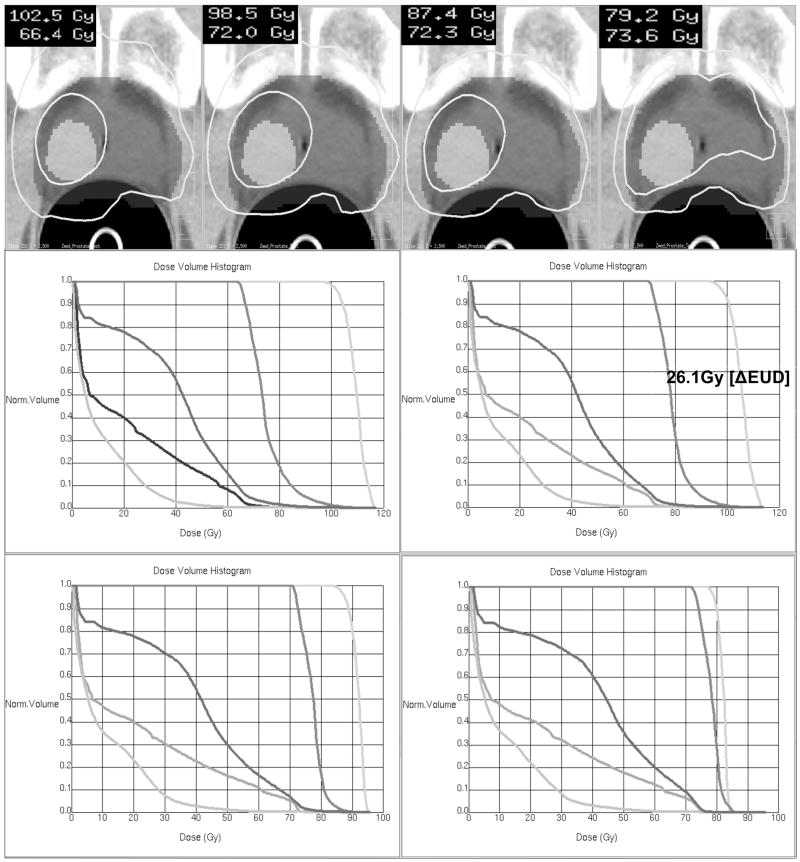
For the four risk-cases: H₊ – L, H₊ – M, H – M, and M – M, Figure 3 illustrates the impact of these risk-parameters on the resulting dose distribution when carrying out risk-adaptive optimization. It is not surprising that for the H₊ – L case we found the largest separation between nodule and rPTV - yielding an average selective boost dose of ΔEUD = 35.4 Gy. For the H₊ – M case, we found the average selective boost dose to be ΔEUD = 26.1Gy. For the H – M case, we found a ΔEUD = 15.1Gy, and for the M - M case, we found a moderate selective boost of ΔEUD = 5 Gy. Note that the risk-classification of the nodule has a direct impact on the boost dose that can be achieved. For instance, as the risk-grade of a nodule moves from intermediate to very high risk, the average dose in the nodule increases by 19.5Gy. On the other hand, if the risk-classification of the rPTV is moved from low to intermediate risk, the average dose increases in the rPTV by 5.4Gy and results in a more homogeneous dosedistribution. Hence, it was found that nodule-risk plays a dominant role in the selective boosting of tumor subvolumes. This effect is expected to be more prominent in a PTV having larger and/or higher-risk nodules. We also observed that the impact of nodulerisk on the rectum and the bladder is negligible for these four risk-cases (cf. Table 3).

Figure 3.

DVHs and isodose maps for the single nodule geometry employing four different risk-scenarios: (a) Very High - Low (H₊-L) (b) Very High - Intermediate (H₊ - M) (c) High – Intermediate (H - M) (d) Intermediate – Intermediate (M – M).

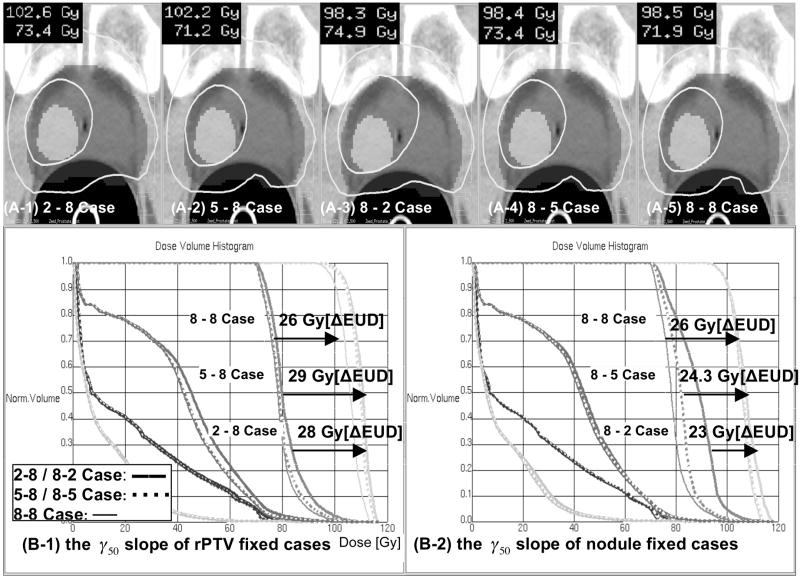
A single nodule geometry has been used to explore the effect of γ₅₀ on riskadaptive optimization. In Table 3, we have summarized the impact of the γ₅₀ -value on risk-adaptive optimization. As can be seen from Table 3, similar selective boosts can be achieved for a given geometry regardless of the steepness of the dose response curves in rPTV or the nodule. Looking at the data presented in Table 3 for a single nodule geometry, one finds that the selective boost achievable varies from an ΔEUD = 33Gy for the 2-2 case (γ₅₀ =2 in both nodule and rPTV) to a ΔEUD = 23Gy for the 8-2 case. Note however, that shallower γ₅₀ values in the rPTV and nodule lead to higher dose inhomogeneity in those volumes and thereby yield higher ΔEUD estimates. Figure 4 shows the impact of the γ₅₀-value on isodose distributions and dose volume histograms for selected combinations of γ₅₀ for the rPTV and the nodule. The isodose lines drawn correspond to the minimal peripheral dose encompassing 95% of the nodule volume and the PTV. Our results indicate that the impact of γ₅₀ on risk-adaptive optimization is less profound than that of D₅₀.

Figure 4.

Isodose distributions and DVHs for a number of γ₅₀ combinations. The isodose distributions were constructed for γ₅₀ values of 2, 5, and 8. In panel (A), the γ₅₀ value of the rPTV remained fixed and that of the nodule was varied. In panel (B), the γ₅₀ value of the rPTV was varied and that of the nodule remained fixed.

The data presented in Table 3 show that for the OAR studied the impact of the value of γ₅₀ or the combination of γ₅₀ values in the rPTV and nodule play a limited role on the sparing of OARs. For instance, the relative volume of rectal wall receiving a dose larger than 70Gy varies from 10.6% to 6.5% for the studied parameter combinations. However, we found that a large value for γ₅₀ in the nodule corresponds to the lowest relative rectal wall volumes above 50Gy, 60Gy, and 70Gy, and to the lowest maximum doses to the bladder independent of the γ₅₀ value of the rPTV. In terms of OAR sparing, this would favor the use of a steep slope for the dose response curve in the nodule and the rPTV.

Figure 5 displays the influence of nodule geometry on risk-adaptive optimization — values of δ = 1 and γ₅₀ = 8 were used for both the nodule and the rPTV. For the twonodule geometry, we found that a selective boost similar to that of the single nodule geometry could be achieved while respecting the OAR objectives. However, for the donut-shaped and large nodule geometry, the selective boosts achieved were lower, namely ΔEUD = 22.9 Gy and ΔEUD = 18.8 Gy, respectively. The reason for this phenomenon is two fold. First, since these nodule geometries compromise a substantial portion of the PTV (16.3 % and 31.8 %, respectively) the dose distribution in the rPTV is necessarily more inhomogeneous thereby yielding higher EUD estimates for the rPTV. Second, due to larger volumes of the OARs that are being irradiated to higher doses for these geometries, the EUD that can be achieved in the nodules is lowered. Hence, the achievable ΔEUD is smaller yielding a smaller selective boost.

Figure 5.

DVHs and isodose maps of the four geometry-cases studied: (a) one nodule (b) two nodules (c) donut-shaped nodule and (d) big nodule.

IV. DISCUSSION

The conventional standard of a well-designed treatment plan has been to require uniform dose coverage of the target while minimizing the irradiated volumes of OARs. The main assumption under this standard is that the physiological makeup of the GTV is reasonably similar throughout. However, as remarked by Mohan et al. [24], when one optimizes a treatment plan purely on dose-to-total-volume, it is inadequate for a tumor since it is a heterogeneous entity with regionally variable risk. Therefore, a heterogeneous dose distribution in the GTV should more effectively achieve optimum tumor-control. To effectively achieve a heterogeneous dose distribution within the GTV, we have developed a risk-adaptive optimization strategy that uses subvolume-based TCP and voxel-based NTCP functions that have been combined into a biological objective function to find the optimal trade-off between TCP and NTCP. A feasibility study of risk-adaptive optimization has been carried out as a function of geometry and risk (D₅₀ and γ₅₀) of tumor subvolumes. In addition, we have quantified the impact of δ on the risk-adaptive optimization process.

All 77 risk-adaptive optimizations, which were repeatedly optimized as a function of δ, clearly show the negligible dependence on δ in the optimization process (std. dev. 0.08 Gy). We, therefore, suggest using UTCP₁ as a combined probability of TCP and NTCP in risk adaptive optimization, resulting in a significant reduction of uncertainty in the value of δ. Brahme [25] remarked that UTCP_δ (i.e. including the delta-value) should be used as the biological objective function to avoid fatal complications or severe side effects. Our study concludes that there is little impact of the δ value on risk-adaptive optimization; however, it was found that D₅₀ and γ₅₀, are crucial parameters to the optimization process. This shows the need for accurate estimation of these clinical parameters. As far as the impact of D₅₀ on the risk-adaptive optimization process is concerned, Figure 3 shows that the tumor subvolumes that exhibit the highest risk receive the largest selective boost, ΔEUD = 35.4Gy, as had been conjectured by Tomé and Fowler [7]. We found that the risk level of a nodule plays a more prominent role in the risk-adaptive optimization process than that of the rPTV. Table 3 quantifies the involvement. This observation is indeed coincident with the well-known hypothesis [7, 8, 17] that the hypoxic or highly malignant tumor cell compartment is essential for the control of tumors even if that compartment is small. Hence, it is important to localize the highest risk subtumor regions and to accurately determine the clinical parameters; D₅₀, γ₅₀. In addition, this supports the rationale of the risk-adaptive optimization method based on tumor subvolumes rather than single voxels. It may not be necessary to quantify the risk of every voxel, but it is important to find the highest risk tumor subvolumes using prognostic processes such as biopsy and physiological imaging.

The impact of γ₅₀ on the risk-adaptive optimization process is considerable less than that of D₅₀ (cf. Figure 4). However, we noted that the γ₅₀-slope will become steeper as more individualized risk data for patients becomes available. A steep value of γ₅₀ maximizes the benefit of selective boosting for a given boost ratio [7]. Hence, riskadaptive optimization will be more efficacious as one obtains more individualized risk data for patients.

From Figure 2, one can see that the selective boosts that can be achieved for donut-shaped and large nodule geometry are more limited. This reinforces the need for early detection of disease. For a given patient, the distribution of the relevant clinical parameters for the target volume may vary considerably from the population-based parameters [26]. Ideally, the individual data are ultimately desirable to be collected for all target volumes. This of course is not practically possible. Thus, we suggest that risk levels for tumor subvolumes be determined from clinical data using physiological imaging techniques combined with biopsy. This will provide the crucial clinical data for risk-adaptive optimization and allow the correlation of physiological imaging techniques to grade, differentiation, and malignancy of tumor determined from the analysis of biopsy samples. In order to avoid a loss of tumor control, it is suggested that the risk of rPTV is treated at least as an intermediate risk due to the finite resolution of molecular imaging techniques [27]. However, in the absence of such data it seems to be a reasonable first step to use population based estimates for D₅₀ and γ₅₀ for the different risk. The impact on the overall TCP when working with population based estimates for D₅₀ and γ₅₀ instead of actual patient based estimates of D₅₀ and γ₅₀ is not clear and remains to be elucidated.

If the optimization process leads to severe cold and hot spots in the rPTV or the nodule, one can compensate for them by adjusting the value for D₅₀ and γ₅₀. For instance, higher values for γ₅₀ for the nodule lead to a more homogenous dose distributions in the nodule.

V. CONCLUSION

The impact of the correlation parameter, δ, on dose-distributions optimized using the risk-adaptive IMRT was evaluated. We found that the value of δ had little effect on riskadaptive optimization — confirmed by an overall standard deviation of 0.08 Gy for 77 optimizations. Since the correlation parameter δ between TCP and NTCP shows little influence on risk-adaptive optimization, it seems sufficient to employ a simple form of the biological objective function such as UTCP₁ in the risk-adaptive optimization process. However, the clinical parameters, D₅₀ and γ₅₀, that represent the risk classification of tumor subvolumes, i.e. their response to radiation insult, had the largest impact on risk-adaptive optimization. Employing risk-adaptive optimization, we found that it was possible to achieve a ΔEUD = 35.4 Gy in tumor subvolumes having the highest risk classification without increasing predicted normal tissue complications in the organs at risk. For all tumor subvolume geometries investigated, we found that the dose to high-risk tumor subvolumes could be increased significantly without increasing normal tissue complications above those expected from a standard treatment plan where the aim is uniform dose coverage of the PTV. Furthermore, the tumor subvolume with the highest risk classification had the largest influence on the design of the riskadaptive dose distribution. Overall, risk-adaptive optimization allows one to escalate dose in tumor subvolumes of highest risk and produce heterogeneous dose distributions that mimic the risk level distribution of the different tumor subvolumes that comprise the tumor while respecting the normal tissue constraints.

VI. APPENDIX

A. Tumor Subvolume-Based TCP model

Derivation of the TCP formulae used above:

$$\mathit{TCP}=\prod _{j=1}^R{\mathit{TCP}}_j^{{\nu }_j}$$ (A-1)

$$\mathit{TCP}(\{D\})=\prod _{j=1}^R{\left(\prod _{i=1}^k{\left[\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{4{\gamma }_{50}^j}}\right]}^{{\nu }_i^j}\right)}^{{\nu }_j}$$ (A-2)

The TCP for a tumor consisting of M voxels and each receiving a uniform dose D can be written as:

$$\mathit{TCP}={(\mathit{TCP})}^{\frac{M}{M}}={\left(\prod _{i=1}^M\mathit{TCP}\right)}^{1/M}$$

Now let us generalize this formula to the case where R subvolumes of the tumor, consisting of M_j voxels each such that ${\sum }_{j=1}^R{M}_j=M$, receive a different uniform dose. Then we can use the above formula to calculate the expected TCP in the entire tumor as:

$$\mathit{TCP}\left({\left\{D_i\right\}}_{j=1}^R\right)={\left(\prod _{j=1}^R\mathit{TCP}{(D_j)}^{M_j}\right)}^{1/M},\text{where}\sum _{j=1}^R{M}_j=M,$$

Note that:

$$\sum _{j=1}^R\frac{M_j}{M}=\sum _{j=1}^R\frac{M_j\times \mathit{Voxel}\mathit{Volume}}{M\times \mathit{Voxel}\mathit{Volume}}=\sum _{j=1}^R\frac{V_j}{V_{\mathit{Tumor}}}=\sum _{j=1}^R{\nu }_j=1.0$$

where ν_j denotes the fractional volume of the j^th subvolume.

Hence, the formula in (A-1) is proved by the following equation:

$$\mathit{TCP}\left({\left\{D_i\right\}}_{j=1}^R\right)=\left(\prod _{j=1}^R\mathit{TCP}{(D_j)}^{{\nu }_j}\right)$$ (A-3)

Here we have assumed that the dose is uniform in each region. Now let us use the same argument as above and write the TCP in the j^th subvolume as:

$${\mathit{TCP}}_j={({\mathit{TCP}}_j)}^{\frac{N}{N}}={\left(\prod _{i=1}^N\mathit{TCP}(D_i^j)\right)}^{\frac{1}{N}},$$

where N is the number of dose voxels in the subvolume j. In the above formula we have assumed that each dose voxel receives the constant dose, $D_i^j$. We can now generalize the above formula again to case of a non-uniform dose distribution in subregion j assuming that each dose voxel receives a constant dose: the above formula then becomes:

$$\mathit{TCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)={\left(\prod _{i=1}^N\mathit{TCP}(D_i^j)\right)}^{\frac{1}{N}},\mathit{where}\mathit{TCP}(D_i^j)=\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{4{\gamma }_{50}^j}}$$

Moreover, we have also made the generalization that each subregion can have different physiological characteristics, and therefore have different $D_{50}^j$ and ${\gamma }_{50}^j$. Factoring the above product into sub-products of term receiving the same dose we find:

$$\mathit{TCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)={\left\{\mathit{TCP}{\left(D_1^j\right)}^{N_1}\cdots \mathit{TCP}{\left(D_k^j\right)}^{N_k}\right\}}^{1/N},\mathit{where}\sum _{i=1}^k{N}_i=N$$

As before note that:

$$\sum _{i=1}^k\frac{N_i}{N}=\sum _{i=1}^k\frac{N_i\times \mathit{Voxel}\mathit{Volume}}{N\times \mathit{Voxel}\mathit{Volume}}=\sum _{i=1}^k\frac{V_i^j}{V^j}=\sum _{i=1}^k{\nu }_i^j=1.0$$

where ${\nu }_i^j$ denotes the fractional volume of the i^th dose bin in the j^th region, $D_i^j$. Accordingly, using this notation the above formula for TCP in any of the R subtumorregions becomes:

$$\mathit{TCP}\left(\left\{D_i^j,{\nu }_i^j\right\}\right)=\prod _{i=1}^k{\left[\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{4{\gamma }_{50}^j}}\right]}^{{\nu }_i^j},\mathit{where}\sum _{i=1}^k{\nu }_i^j$$ (A-4)

Hence, the overall subvolume based TCP in (A-2) is obtained by substituting (A-4) into (A-3):

$$\mathit{TCP}(\{D\})=\prod _{j=1}^R{\left[\mathit{TCP}\left(\left\{D_i^j,{\nu }_i^j\right\}\right)\right]}^{{\nu }_j}=\prod _{j=1}^R{\left(\prod _{i=1}^k{\left[\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{4{\gamma }_{50}^j}}\right]}^{{\nu }_i^j}\right)}^{{\nu }_j}$$

A.2 Deviation of the gradient of TCP for optimization

The gradient calculation of TCP in each tumor subvolume consisting N voxels is given by:

$$\begin{array}{c}\mathit{grad}\left[\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)\right]=\nabla \mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right),\\ \nabla \mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)=\left(\begin{array}{c}{\partial }_{D_1}\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)\\ ⋮\\ {\partial }_{D_N}\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)\end{array}\right),\mathit{and}\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)=\prod _{i=1}^N\mathit{TCP}{(D_i)}^{\frac{1}{N}},\end{array}$$

where, N is the number of voxels in the tumor subvolume under consideration.

Let us evaluate the i^th component of the gradient:

$${\partial }_{D_i}\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)=\frac{\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)}{N}\frac{{\partial }_{D_i}\mathit{TCP}(D_i)}{\mathit{TCP}(D_i)}$$

Evaluation of the derivative with respect to D_i yields the following expression:

$${\partial }_{D_i}\mathit{TCP}(D_i)=\frac{4{\gamma }_{50}}{D_i}{\left(\frac{D_{50}}{D_i}\right)}^{4{\gamma }_{50}}\mathit{TCP}{(D_i)}^2$$

Putting everything together the i^th component of the gradient of TCP is found to be:

$${\partial }_{D_i}\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)=\frac{4{\gamma }_{50}}{N{D}_i}{\left(\frac{D_{50}}{D_i}\right)}^{4{\gamma }_{50}}\mathit{TCP}(D_i)\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)$$

Therefore, the gradient vector of TCP in each subtumor-region consisting N voxels is given by:

$$\mathit{grad}\left(\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)\right)=\left(\begin{array}{c}\frac{4{\gamma }_{50}}{N{D}_1}{\left(\frac{D_{50}}{D_1}\right)}^{4{\gamma }_{50}}\mathit{TCP}(D_1)\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)\\ ⋮\\ \frac{4{\gamma }_{50}}{N{D}_i}{\left(\frac{D_{50}}{D_i}\right)}^{4{\gamma }_{50}}\mathit{TCP}(D_i)\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)\\ ⋮\\ \frac{4{\gamma }_{50}}{N{D}_N}{\left(\frac{D_{50}}{D_N}\right)}^{4{\gamma }_{50}}\mathit{TCP}(D_N)\mathit{TCP}\left({\left\{D_i\right\}}_{i=1}^N\right)\end{array}\right)$$

B. Voxel Based NTCP Model

Let us assume that each voxel of the j^th OAR, denoted by OAR_j, receives a constant dose $D_i^j$, then we can write the total NTCP in OAR_j as:

$$\mathit{NTCP}\left(D_i^j\right)=1-{\left(1-\mathit{NTCP}\left(D_i^j\right)\right)}^{\frac{N}{N}}=1-\prod _{i=1}^N{\left(1-\mathit{NTCP}\left(D_i^j\right)\right)}^{\frac{1}{N}},$$ (B1)

where N is the number of dose voxels in OAR_j. In the above formula we have assumed that each dose voxel receives the constant dose, $D_i^j$. We can now generalize the above formula again to case of a non-uniform dose distribution in OAR_j assuming that each dose voxel receives a constant dose: the above formula then becomes:

$$\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)=1-\prod _{i=1}^N{\left[1-\mathit{NTCP}(D_i^j)\right]}^{\frac{1}{N}},\mathit{where}\mathit{NTCP}(D_i^j)=\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{\frac{4}{\sqrt{2\pi }{m}_j}}}$$ (B2)

Factoring the above product into sub-products of term receiving the same dose we find:

$$\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)=1-{\left\{{\left[1-\mathit{NTCP}\left(D_1^j\right)\right]}^{N_1}\cdots {\left[1-\mathit{NTCP}\left(D_l^j\right)\right]}^{N_l}\right\}}^{1/N},\mathit{where}\sum _{i=1}^l{N}_i=N$$

As before note that:

$$\sum _{i=1}^l\frac{N_i}{N}=\sum _{i=1}^l\frac{N_i\times \mathit{Voxel}\mathit{Volume}}{N\times \mathit{Voxel}\mathit{Volume}}=\sum _{i=1}^l\frac{V_i^j}{V_{OA{R}_J}}=\sum _{i=1}^l{\nu }_i^j=1.0$$

where ${\nu }_i^j$ denotes the fractional volume of the i^th dose bin in OAR_j, $D_i^j$. Accordingly, using this notation the above formula for NTCP in any of the OAR_j becomes:

$$\mathit{NTCP}\left(\left\{D_i^j,{\nu }_i^j\right\}\right)=1-\prod _{i=1}^l{\left(1-\mathit{NTCP}(D_i^j)\right)}^{{\nu }_i^j},\text{where}\mathit{NTCP}(D_i^j)=\frac{1}{1+{\left(\frac{D_{50}^j}{D_i^j}\right)}^{\frac{4}{\sqrt{2\pi }{m}_j}}}\text{and}\sum _{i=1}^l{\nu }_i^j=1$$ (B3)

B.2 Deviation of the gradient of voxel-bnased NTCP

The gradient of voxel-based NTCP in j^th normal tissue is given by:

$$\mathit{grad}\left(\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)\right)=\nabla \mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)$$

As above we now proceed amd evaluate the i^th component of this gradient:

$${\partial }_{D_i}\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)=\frac{1-\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)}{N}\frac{{\partial }_{D_i}\mathit{NTCP}(D_i^j)}{(1-\mathit{NTCP}(D_i^j))}$$ (B-4)

Evaluation of the derivative with respect to D_i yields the following expression:

$${\partial }_{D_i}\mathit{NTCP}(D_i^j)=\frac{4}{\sqrt{2\pi }{m}_j{D}_i^j}{\left(\frac{D_{50}}{D_i^j}\right)}^{\frac{4}{\sqrt{2\pi }{m}_j}}\mathit{NTCP}{(D_i^j)}^2$$

Putting everything together the i^th component of the gradient of NTCP is found to be:

$${\partial }_{D_i}\mathit{NTCP}\left({\left\{D_i\right\}}_{i=1}^N\right)=\frac{4}{\sqrt{2\pi }{m}_j{D}_i^j}{\left(\frac{D_{50}}{D_i^j}\right)}^{\frac{4}{\sqrt{2\pi }m}}\frac{\mathit{NTCP}{(D_i^j)}^2\left[1-\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)\right]}{N[1-\mathit{NTCP}(D_i^j)]}$$

Hence, the gradient vector of NTCP for an OAR consisting of N voxel is given by:

$$\mathit{grad}\left(\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)\right)=\left(\begin{array}{c}\frac{4}{\sqrt{2\pi }{m}_j{D}_1^j}{\left(\frac{D_{50}}{D_1^j}\right)}^{\frac{4}{\sqrt{2\pi }{m}_j}}\frac{\mathit{NTCP}{(D_1^j)}^2\left[1-\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)\right]}{N[1-\mathit{NTCP}(D_1^j)]}\\ ⋮\\ \frac{4}{\sqrt{2\pi }{m}_j{D}_i^j}{\left(\frac{D_{50}}{D_i^j}\right)}^{\frac{4}{\sqrt{2\pi }{m}_j}}\frac{\mathit{NTCP}{(D_i^j)}^2\left[1-\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)\right]}{N[1-\mathit{NTCP}(D_i^j)]}\\ ⋮\\ \frac{4}{\sqrt{2\pi }{m}_j{D}_N^j}{\left(\frac{D_{50}}{D_N^j}\right)}^{\frac{4}{\sqrt{2\pi }{m}_j}}\frac{\mathit{NTCP}{(D_N^j)}^2\left[1-\mathit{NTCP}\left({\left\{D_i^j\right\}}_{i=1}^N\right)\right]}{N[1-\mathit{NTCP}(D_N^j)]}\end{array}\right)$$

C. Deviation of the gradient of voxel-based UTCP₁ AND UTCP_δ

The gradient of voxel-based UTCP₁ of all tumor subvolumes and normal tissues is given by:

$$\begin{array}{c}\mathit{grad}({\mathit{UTCP}}_1(\left\{D\right\}))=\nabla {\mathit{UTCP}}_1(\{D\}),\text{and}\\ \nabla {\mathit{UTCP}}_1(\{D\})=(1-\mathit{NTCP}(\left\{D\right\}))\nabla \mathit{TCP}(\{D\})-\mathit{TCP}(\{D\})\nabla \mathit{NTCP}(\{D\})\end{array}$$

In order to evaluate the gradient of UTCP₁ we need to evaluate the gradient of the overall TCP and NTCP function. Let us first evaluate the gradient of overall TCP function of a tumor having R tumor subvolumes:

$$\nabla \mathit{TCP}(\{D\})=\nabla \left(\prod _{j=1}^R{\mathit{TCP}}_j^{{\nu }_j}\right)=\nabla {\mathit{TCP}}_1^{{\nu }_1}{\mathit{TCP}}_2^{{\nu }_2}\cdots {\mathit{TCP}}_R^{{\nu }_R}+\cdots +{\mathit{TCP}}_1^{{\nu }_1}\cdots {\mathit{TCP}}_{R-1}^{{\nu }_{R-1}}\nabla {\mathit{TCP}}_R^{{\nu }_R}$$

where R denotes the number of tumor subvolumes. The gradient of ${\mathit{TCP}}_j^{{\nu }_j}$ in the jth term in the sum above for the overall TCP gradient can be evaluated using the chain rule as follows:

$${\partial }_{{\mathit{TCP}}_j}\left({\mathit{TCP}}_j^{{\nu }_j}\right)\nabla {\mathit{TCP}}_j={\nu }_j{\mathit{TCP}}_j^{{\nu }_j}\frac{\nabla {\mathit{TCP}}_j}{{\mathit{TCP}}_j}$$

Substituting this expression in all terms of sum above we find the gradient of overall TCP of all tumor subvolumes to be:

$$\nabla \mathit{TCP}(\{D\})=\mathit{TCP}(\{D\})\sum _{j=1}^R{\nu }_j\left(\frac{\nabla {\mathit{TCP}}_j}{{\mathit{TCP}}_j}\right)$$

The gradient of TCP in each tumor subvolume, $\nabla {\mathit{TCP}}_j\left({\left\{D_i\right\}}_{i=1}^N\right)$, has been derived above.

Now, the gradient of overall NTCP for normal tissues is similarly evaluated as:

$$\begin{array}{l}\nabla \mathit{NTCP}(\{D\})=\nabla \left[1-\prod _{j=1}^Q[1-{\mathit{NTCP}}_j]\right]\\ =\nabla {\mathit{NTCP}}_1(1-{\mathit{NTCP}}_2)\cdots (1-{\mathit{NTCP}}_Q)+\cdots +(1-{\mathit{NTCP}}_1)\cdots (1-{\mathit{NTCP}}_{Q-1})\nabla {\mathit{NTCP}}_Q\end{array}$$

where Q is the number of normal tissues. The gradient of NTCP in each normal tissue, ∇NTCP_j, has been derived above. Using the identity $1-\mathit{NTCP}={\displaystyle \prod _{j=1}^Q}(1-{\mathit{NTCP}}_j)$ find after some minor manipulation the following fro the overall NTCP gradient:

$$\nabla \mathit{NTCP}(\{D\})=(1-\mathit{NTCP})\sum _{j=1}^Q\frac{\nabla {\mathit{NTCP}}_j}{(1-{\mathit{NTCP}}_j)}$$

Therefore, the gradient of UTCP₁ is found to be:

$$\begin{array}{l}\nabla {\mathit{UTCP}}_1(\{D\})=\nabla \left[\mathit{TCP}(\{D\})(1-\mathit{NTCP}(\left\{D\right\}))\right]\\ =\mathit{TCP}(\{D\})(1-\mathit{NTCP}(\{D\}))\left(\sum _{j=1}^R{\nu }_j\left(\frac{\nabla {\mathit{TCP}}_j}{{\mathit{TCP}}_j}\right)+\sum _{j=1}^Q\frac{\nabla {\mathit{NTCP}}_j}{(1-{\mathit{NTCP}}_j)}\right)\end{array}$$

Furthermore, the gradient of UTCP_δ is expressed by:

$$\begin{array}{l}\nabla {\mathit{UTCP}}_{\delta }(\{D\})=\nabla \left[(\mathit{TCP}(\left\{D\right\})-\mathit{NTCP}(\left\{D\right\}))+\delta (1-\mathit{TCP}(\left\{D\right\})\mathit{NTCP}(\left\{D\right\}))\right]\\ =\left(1-\delta \mathit{NTCP}(\{D\})\right)\mathit{TCP}(\{D\})\sum _{j=1}^R{\nu }_j\left(\frac{\nabla {\mathit{TCP}}_j}{{\mathit{TCP}}_j}\right)-\left\{1-\delta +\delta \mathit{TCP}(\{D\})\right\}(1-\mathit{NTCP})\sum _{j=1}^Q\frac{\nabla {\mathit{NTCP}}_j}{(1-{\mathit{NTCP}}_j)}\end{array}$$

where, R denotes the number of tumor subvolumes, and Q denotes the number of normal tissues. Delta (0 ≤ δ ≤ 1) denotes the fraction of the population for which TCP and NTCP are uncorrelated. Therefore, UTCP_δ reduces to UTCP₁ as the value of delta approaches 1.0.