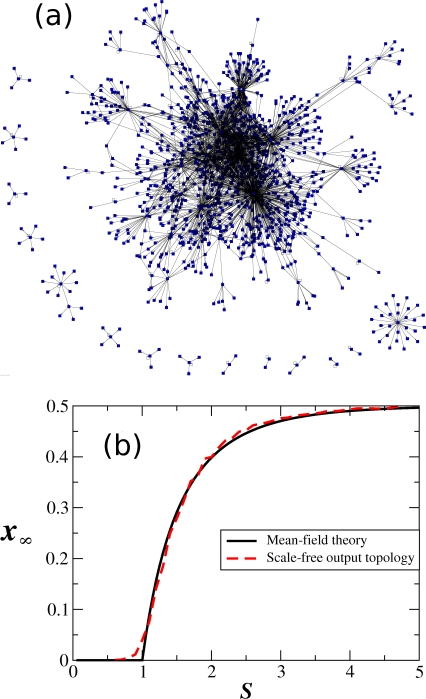
Figure 1. Order-chaos phase transition in Boolean networks with realistic topologies.

(a) Graphic representation of the gene transcription network of E. coli K-12. For this network the probability for a given gene to have K regulators is P(K) = e ^−z z^K/K! (Poisson input topology), whereas the probability to be a regulator to n other genes is P(n) = Cn ^−γ (scale-free output topology). (b) Phase transition diagram showing x _∞ as a function of S. The solid line in black is the theoretical result predicted by the mean-field theory. The dashed line in red was computed numerically for randomly constructed Boolean networks with N = 1000, Poisson input topology and scale-free output topology. The Boolean functions were randomly generated with a probability of gene expression p = 0.5. Remarkably, the phase transition predicted by the mean field theory is identical to the one obtained for random Boolean networks with topologies statistically equivalent to the real ones.