Modeling Analytical Ultracentrifugation Experiments with an Adaptive Space-Time Finite Element Solution for Multicomponent Reacting Systems

Abstract

We describe an extension of the adaptive space-time finite element method (ASTFEM) used in the solution of the Lamm equation to the case of multicomponent reacting systems. We use an operator splitting technique to decouple the sedimentation-diffusion process from the reaction process. The former is solved with an ASTFEM approach based on the Petrov-Galerkin method and on adaptive moving grids, and the latter is solved with the implicit midpoint Euler's method. Our solution can effectively eliminate the sedimentation errors for each component or species involved in the reaction, and it is free from oscillation near the cell bottom. It offers second-order accuracy, and guarantees conservation of mass without any additional postprocessing, and it permits modeling of multicomponent, equilibrating systems where the reaction rate can be kinetically controlled between an instantaneous reaction and a noninteracting mixture. The proposed ASTFEM solution provides improved efficiency and accuracy compared to classical approaches, especially when medium-sized and large molecules are modeled.

INTRODUCTION

Analytical ultracentrifugation is an effective technique for characterizing biological macromolecules in solution. It permits the determination of composition, assembly state, and conformational properties of biological macromolecules in a near-physiological solution environment, where pH, ionic strength, temperature, and concentration can be conveniently controlled. The sedimentation and diffusion transport of a single, ideal solute in the analytical ultracentrifugation cell is described by the Lamm equation (1). Recently, we introduced an efficient and accurate adaptive space-time finite element solution of the Lamm equation (ASTFEM (2)). While this approach is sometimes used to model interacting systems, this treatment does not take the dynamic properties of the reaction into account, where the concentration profile may be perturbed during the sedimentation and diffusion transport due to reactions occurring between the sedimenting solutes. By including reaction source terms in the Lamm equation, a more rigorous approach for modeling reacting systems can be proposed which includes a description of the equilibrium constants and the kinetic rate constants of the reactions. Classical finite element solutions for reacting systems based on uniform grids of the Lamm equation have been proposed earlier by Claverie (3) and Todd et al. (4), and a software program based on these approaches has been developed by Stafford and Sherwood (5). An improved solution, the so-called moving hat method, for noninteracting solutes and the case of instantaneously reacting reversible self-associations has been proposed by Schuck (6).

For systems with large molecular weights and high sedimentation speeds, classical methods can suffer from large errors originating from the sedimentation term. Such errors manifest themselves in a smoothing of the concentration boundary and in oscillations of the solution at the bottom of the cell. This smoothing effect causes an overestimation of the diffusion coefficient (with a concomitant underestimation of the molecular weight), and in severe cases the oscillations can propagate back into the solution column, affecting the entire solution. The moving hat method (6) eliminates the sedimentation error in the numerical solutions by shifting the grids toward the cell bottom at the same speed as the sedimenting solute. The moving hat method represents a major improvement over Claverie's method for single species models, but it does not eliminate the oscillations of the solution near the cell bottom, fails to account for the differences in sedimentation speed of multiple components in the reacting case, and requires postprocessing of the solution to assure mass conservation. In the following discussion we refer to “components” to mean both distinct solutes encountered in hetero-associating systems, and also oligomeric species encountered in reversible self-associating systems.

The ASTFEM approach (2) uses a grid similar to that from the moving hat method to eliminate sedimentation error, but also carefully refines the grid spacing at the bottom of the cell which eliminates the oscillations seen in other solutions. In addition, due to the rigorous space-time finite element formulation, it does not require any postprocessing to maintain conservation of mass. Here we describe an extension of the ASTFEM approach to the general case which also includes reacting systems of multiple components, and offers a direct solution of the Lamm equations involving sedimentation, diffusion, and the reaction mechanisms.

By extending ASTFEM to multicomponent reacting systems we encounter the problem that the grids used for ASTFEM (2) (as well as for the moving hat method (6)) move with different speeds for different components in the system, but the reaction should occur on a common grid. To overcome this difficulty, we use a special type of the Petrov-Galerkin method, the localized adjoint method proposed by Bouloutas and Celia (7) and Celia et al. (8), to construct the finite element solutions. A key point in this approach is to use different test functions to follow different sedimentation speeds of each Lamm equation, while keeping all the unknown partial concentrations defined on the same grid. This treatment not only eliminates the sedimentation errors for all components, but also avoids the need of interpolation of numerical solutions in the process of simulation. We also include a specially designed adaptive grid with high mesh densities near the cell bottom, which eliminates the oscillation of the sedimentation profile near the bottom of the cell.

To treat the reaction terms in the multicomponent systems efficiently, we employ an operator splitting technique proposed by Strang (9). It separates the sedimentation-diffusion process from the reaction process in each time step. The former corresponds to a system of homogeneous Lamm equations which can be solved independently for each component, while the latter is a system of ordinary differential equations (ODE), which can be solved independently for each radial point. Both of them can be implemented in parallel, promising performance advantages with increasingly common multicore computer chip architectures.

The combination of ASTFEM and the operator splitting method for multicomponent reacting systems offers several notable advantages:

1. Approximation errors originated from sedimentation terms are effectively eliminated for all components.

2. Numerical solutions are free from oscillation near the bottom of the cell.

3. The solution is of second-order accuracy in both space and time variables; namely, when the step sizes in radial and time directions are halved, the solution error is approximately reduced by a factor of 4.

4. The mass conservation is guaranteed automatically.

We tested our solution with several examples including monomer-dimer and monomer-trimer-hexamer associations. It is found that for systems with large molecules with large s/D ratios, the accuracy of our solution is particularly advantageous over the classical finite element method (FEM) based on fixed adaptive meshes, while the computational work of the two are comparable. For systems with relatively small molecules or velocity experiments at low rotor speed, our scheme is only slightly better than the fixed mesh method. These conclusions are true for all reaction rates ranging from instantaneous reaction to noninteraction. It should be noted that for cases where improved accuracy is not required, our method achieves the same accuracy as other methods with a reduced computational effort, which is particularly advantageous for recently introduced optimization methods that require a large number of repeated evaluations of the Lamm equation (10–13).

NUMERICAL SCHEME FOR MULTICOMPONENT REACTING SYSTEMS

Let m and b be the radii at the meniscus and at the bottom of the cell, and ω be the angular velocity. Let C_k(r, t) be the partial concentration of the k^th component. The values s_k and D_k are the component's sedimentation and diffusion coefficients, respectively. Then the velocity experiment of multicomponent reacting systems can be modeled by the following partial differential equations,

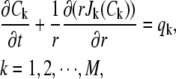(1)

where

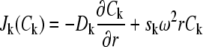is the total flux for the k^th component, and q_k = q_k(C₁, ···, C_M) is a function characterizing the contribution to the change in concentration of the k^th component from the reactions in the system. The change in concentration is determined by the equilibrium constants and reaction rates, as well as the binding stoichiometries of the components. The boundary condition for Eq. 1 requires that there is no flux at both ends of the cell, i.e., J_k(C_k) = 0 at the meniscus and at the bottom for all k = 1, 2, ···, M.

Operator splitting scheme decoupling sedimentation-diffusion and reaction

There are several issues to be considered when we choose an efficient and robust discretization scheme for solving Eq. 1. First of all, a straightforward discretization of Eq. 1 couples the sedimentation-diffusion and the reaction processes. Depending on the solutes of the system, these processes can occur on significantly different timescales. If we treat the reaction terms explicitly as proposed earlier by Claverie (3), then excessively small time steps will be required to maintain the stability of the scheme, particularly when the reaction rates are high. On the other hand, if the reaction term is treated implicitly, then the coefficient matrix for the linear system of algebraic equations has to be recomputed at every time step, which can be very time-consuming. In addition, suppose we use N_G grid points in the radial direction for discretization, then a coupled discretization would result in a large system of M × N_G equations at every time step.

To address these issues, we use an operator splitting method to decouple the sedimentation-diffusion transport from the reaction process. With an operator splitting method, we can alternate between the simulation of the pure sedimentation-diffusion process and the calculation of the pure reaction process. As a result, each process can be solved independently and efficiently. This idea has been widely used in simulations of complex systems involving chemical and biological reactions such as combustion, air pollution, and aquatic chemistry (for examples, see (14,15)). In analytical ultracentrifugation, the approach chosen by Cann and Goad (16) using finite differencing, and later by Todd and Haschemeyer (4) using finite elements, for the simulation of instantaneous associations is an example of an operator splitting method. In their numerical scheme, each sedimentation-diffusion step is followed by an instantaneous reaction step by recalculating the partial concentrations of all components according to the reaction equations. In this approach, a kinetic limitation on the reaction cannot be considered. Among many versions of the splitting schemes, we choose a sequential noniterative scheme originally proposed by Strang (9) for its efficiency (no iterations are needed) and its second-order (in time) accuracy (refer to (14) for examples of model analysis and comparison of several operator splitting schemes).

With the Strang-splitting method, the evolution of the solution from time t_n to t_n+1 = t_n + δt consists of three stages:

• Stage 1: Sedimentation-diffusion from time t_n to t_n+1/2 = t_n + δt/2.

• Stage 2: Reaction for a time period of δt, say from t_n to t_n+1.

• Stage 3: Sedimentation-diffusion from t_n+1/2 to t_n+1.

The initial condition for each stage is chosen to be the solution at the end of the previous stage, and the solution at t_n+1 in Stage 3 is taken as the approximate solution to Eq. 1 at time t_n+1. This procedure can be described in formulas as follows: first we solve for each 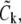k = 1, 2, ···, M, separately from a sedimentation-diffusion equation,

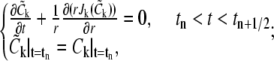(2)

then we solve for all 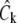from the following system of ODEs for the reaction

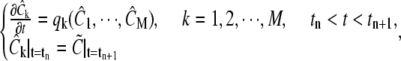(3)

and finally we solve again for each 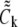from

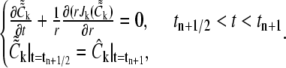(4)

Note that each equation in Stage 1 is a homogeneous Lamm equation. These equations are independent of each other, and can be solved separately and in parallel. Stage 3 is a similar case. Stage 2 involves a system of ODEs for each radial position. At different radial points, these systems are independent of each other, hence can be solved separately. In the next two subsections we describe the solutions in the three stages. Since Stage 3 is identical to Stage 1, except with different initial conditions, we only explain the solution for Stages 1 and 2 in detail.

Adaptive space-time finite element method (ASTFEM) for sedimentation-diffusion equations

First, we consider the solution of the Lamm equations in Stage 1. As demonstrated in our previous work (2) and by Schuck (6), the use of moving grids for finite element discretizations of Eq. 2 minimizes sedimentation errors and improves substantially the solution accuracy of the Lamm equation. However, using ASTFEM or the moving hat method directly to solve a reacting multicomponent system is not advisable because the solutions for different components would be defined on different grids, due to the dependence of the ideal grid speed on the sedimentation coefficient of each component. This is a problem because calculations in Stage 2 require all components to be specified on the same grid.

An alternative approach, which was implemented by Schuck (6) for the moving hat method, calculates a finite element solution for each component using the same moving grid either determined by the sedimentation speed of one of the components, or determined by the average of the speeds of all reacting components. This option represents an unsatisfactory compromise because sedimentation errors are only partially canceled. Clearly, when the sedimentation speeds for the reacting components in the system are very different, the sedimentation errors for one or more components in the reaction will remain significantly different from the average, and the overall solution accuracy will suffer.

To overcome this difficulty, we use a specially adapted Petrov-Galerkin method and the localized adjoint method proposed by Bouloutas and Celia (7) and Celia et. al. (8) to construct the space-time finite element scheme. More specifically, we define the approximate solution for all components on the same mesh, but define the test functions on different meshes, where each mesh follows the sedimentation speed of a particular component to eliminate the sedimentation errors for the corresponding Lamm equation in Eq. 2. The idea of using the localized adjoint method has been extensively studied and used to develop the various Eulerian-Lagrangian localized adjoint methods; for other examples, we refer the reader to the literature (17–19).

To introduce this method, we first derive the weak formulation of Eq. 2. For each k = 1, 2, ···, M, let v be an arbitrary function defined on m < r < b and on t_n < t < t_n+1/2. We then multiply with r v on both sides of Eq. 2 and integrate over the space-time slab [m, b] × [t_n, t_n+1/2]. It follows from integration by parts (with respect to r) and the zero flux boundary condition that

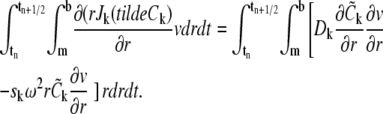(5)

Also, it follows from integration by parts (with respect to t) that

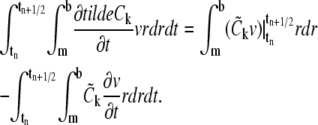(6)

Combining the above two formulas, we obtain the weak formulation of Eq. 2,

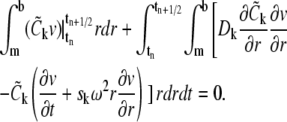(7)

It was observed by Barrett and Morton (20) that, by choosing the functions v(r, t) such that

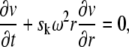(8)

the last two terms on the left-hand side of Eq. 7 would be canceled, and Eq. 7 essentially corresponds to a pure diffusion problem whose solution can be easily obtained. Furthermore, Eq. 8 can be fulfilled if v is constant along suitable curves r = r(t). Indeed, by the chain rule for derivatives, v(r(t), t) = const. on such curves implies that

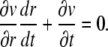After subtracting the above equation from Eq. 8, we obtain an equation for defining the curve r = r(t) as

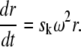The solution is

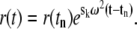(9)

These curves are called the characteristic lines of the sedimentation equation. A key point in constructing the ASTFEM scheme for each of the Lamm equations in Stage 1 is to choose the test functions such that they are constant along the characteristic lines determined by different values of s_k as in Eq. 9.

Space-time mesh and basis functions

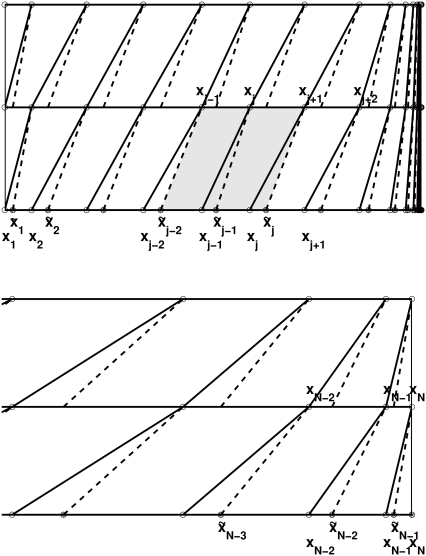
To construct our adaptive space-time finite element scheme for Eq. 2, we need to specify a common space-time mesh on which the approximate solutions are defined for all components. We also need to select M different space-time meshes aligned approximately with M sets of characteristic lines described in Eq. 9 to define the test functions. Suppose N_G is the total number of points used in the radial direction, and 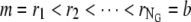are their radial coordinates. We can connect each pair of points{(r_j, t_n), (r_j+1, t_n+1/2)}, j = 1, ···, N_G – 1, with straight line segments. Then the space-time slab [m, b] × [t_n, t_n+1/2] is divided into N_G – 2 quadrilateral and 2 triangular (one at each end) elements as follows (see Fig. 1):

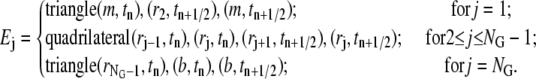We now introduce a basis function 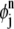associated with each grid point (r_j, t_n):

Inside each element, 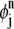is defined as the pull-back of a linear or bilinear polynomial defined on the standard triangular or quadrilateral element (refer to (2) for more details). The expression 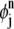is a zero function in all elements except E_j and E_j+1, which are adjacent to the line through (r_j, t_n) and (r_j+1, t_n+1/2). Similarly, we introduce the basis function 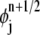associated with grid (r_j, t_n+1/2):

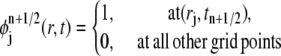and 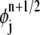is a zero function in all elements except E_j–1 and E_j.

FIGURE 1.

Space-time mesh (solid lines) used to define all approximate solutions and the mesh used to define the test functions for one particular component (dotted lines).

Now, let 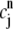and 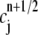be the approximate values of 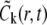at the grid points (r_j, t_n) and (r_j, t_n+1/2), respectively. We define the following continuous function 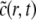to approximate 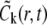(to simplify the notation, throughout this and the next subsections we omit the dependence of on component index k, with the understanding that refers only to the k^th component):

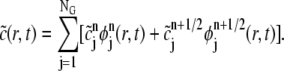(10)

It follows that on each element E_j, 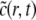is the pull-back of a linear or bilinear polynomial defined on the standard elements with the specified values at the element vertices.

Next, we describe how to choose the test functions for the k^th component to make Eq. 8 hold approximately. For this purpose, let 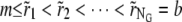be a set of radial points on the line t = t_n. Their positions are determined such that the line from 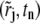to (r_j+1, t_n+1/2) follows approximately the characteristic lines given by Eq. 9. Note that the characteristic lines are determined by the sedimentation speed s_k. Hence different components correspond to different sets of 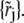In the next section we describe the details on how to choose their positions. We connect 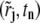and (r_j+1, t_n+1/2) for all j = 1, 2, ···, N_G – 1 to form N_G – 1 quadrilateral elements and one triangular (the rightmost) element:

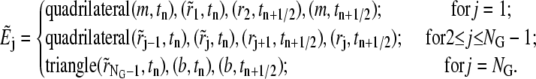We introduce a series of test functions ψ_j(r, t) as follows: For 2 ≤ j ≤ N_G – 1, we define the values of ψ_j on the grid points as

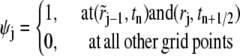and extend ψ_j into each element 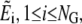by using the pull-back of linear or bilinear polynomials on standard elements as before. For j = 1, we require

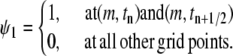For j = N_G, we require

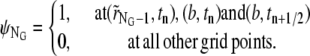It is noted that each ψ_j is nonzero only in two elements, and next to the line through 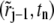and (r_j, t_n+1/2).

System of linear equations

Now we consider the system of algebraic equations resulting from the finite element discretization of Eq. 2. First, we put the approximate solution expressed as Eq. 10 into the weak formulation in Eq. 7, and choose v = ψ_j. We have for each i = 1, 2, ···, N_G that

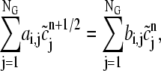(11)

where

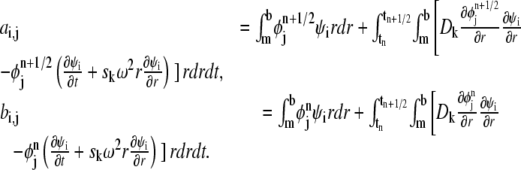A finite element approach where the test functions {ψ_j} are different from the basis functions {φ_j} as we have implemented here is referred to as the Petrov-Galerkin method. Let matrices A = (a_{i, j}) and B = (b_{i, j}), and let vectors 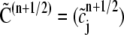and 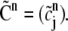Then Eq. 11 can be put into matrix form:

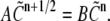(12)

The integrals used in the equations for a_{i, j} and b_{i, j} can be computed numerically with quadrature rules on the standard elements (see (21) for more details). Since a_{i, j} and b_{i, j} are independent of time, this calculation is only performed once for the entire simulation. 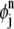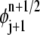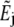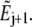In addition, note that and are nonzero only in two space-time elements, E_j and E_j+1, and that test function ψ_j is only nonzero in two elements, and If 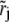lies in between r_j and r_j+1 for all j (as is in our case, see Adaptive Grids for ASTFEM of Multicomponent Systems below), then the nonzero region (also called the support) of 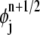intersects the nonzero region of test function ψ_i only when j = i – 1, i, i + 1, i + 2. Similarly, the support of 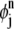intersects the support of test function 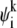only when j = i – 2, i – 1, i, i + 1. This implies that both matrices A and B have only four nonzero diagonal lines, and that the linear system Eq. 12 can be solved by using Gaussian elimination similarly to the tridiagonal linear systems (it requires ∼17 N_G arithmetic operations compared with 13 N_G operations for solving tridiagonal systems).

ODE integrator for the reaction process

In this section we consider the solution of the system of ODEs describing the reaction process in Stage 2 of the operator splitting method. There are a number of ODE integrators that can be used to obtain an approximate solution of Eq. 3. Given the fact that operator splitting introduces a second-order error O(δt)² into the numerical solution, it is not necessary to employ a higher order ODE integrator to compute the approximate solution from t_n to t_n+1. Considering also that Eq. 3 may become very stiff when the reaction rates are high, explicit integrators may put severe restrictions on the time-step size to maintain the stability of the calculation. Hence we choose the implicit midpoint Euler scheme to discretize Eq. 3. More precisely, at each grid point r_j, 1 ≤ j ≤ N_G, we find all 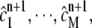satisfying

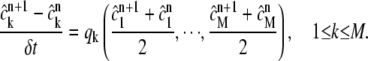(13)

This is a nonlinear system of M algebraic equations which can be solved with Newton's iterative method, if an analytical solution for the equation is not available.

Brief analysis of our scheme

First, note that for the extreme case of noninteracting systems, we have q_k = 0. Hence 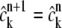in Stage 2, and our operator splitting scheme is reduced to the Petrov-Galerkin method for M independent Lamm equations. In the extreme case of instantaneous reacting systems, the midpoint Euler's method for the second stage of operator splitting becomes

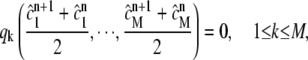which means that the reaction equilibrium is imposed in the middle of t_n and t_n+1. This is slightly different from Todd and Haschemeyer's treatment which imposes the equilibrium at the end of each time step. Nevertheless, both treatments should produce a second-order accuracy in the instantaneous reacting cases. For general finite rate reactions, the midpoint Euler formula is a second-order scheme, thus the solution error for Stage 2 is proportional to (δt)². It is on the same order as the discretization error introduced by the operator splitting for the original system; see Carrayrou et al. (14). Furthermore, the space-time finite element discretization used in Stages 1 and 3 is equivalent to Crank-Nicolson discretization in time (2), the solution errors in these two stages are proportional to N⁻² and (δt)². Therefore, when δt is chosen proportional to N⁻¹, the overall error of this three stage operator splitting scheme will be of order N⁻². We determine δt according to N as described by Eq. 15 in the next section. Our numerical tests confirm the second-order accuracy of the solution in all tested cases.

One might wonder if using higher than second-order ODE integrators in Stage 2 would improve the overall solution accuracies. For comparison, we tested replacing the midpoint Euler formula with a higher order semi-implicit Bulirsch-Stoer method; for details, refer to Press et al. (22). This is a popular time integrator which offers both the higher order accuracy and the capability of dealing with stiff ODEs. Our tests indicate that for the entire range of reaction rates (from instantaneous reaction to noninteraction), no significant improvement of the overall solution accuracy can be observed with the higher order integrator for Eq. 3, while its computational cost is at least several times higher than the midpoint Euler method.

Another important aspect of our scheme is that the total mass conservation is guaranteed automatically. Since the test functions used in both Stages 1 and 3 satisfy

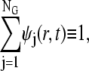we can derive from Eq. 7 and the initial conditions for each k = 1, 2, ···, M that

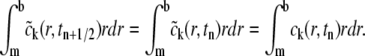Similarly,

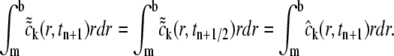Furthermore, by the law of mass conservation for reactions 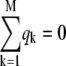at all r and t, we have from Eq. 13 that

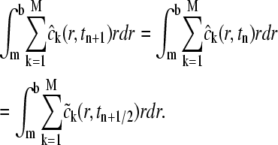Combining the above three equations and noting that 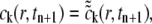we have conservation of the total concentration

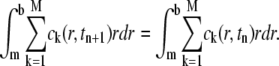ADAPTIVE GRIDS FOR ASTFEM OF MULTICOMPONENT SYSTEMS

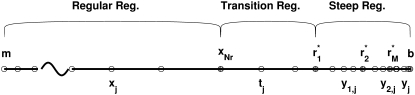
Next we discuss the construction of radial grids for the ASTFEM solution. First, we choose the radial positions r_j for the common mesh where all unknown partial concentrations are defined. Analogous to the ASTFEM approach introduced in Cao and Demeler (2) for noninteracting systems, the grid points in the radial direction are grouped into three different regions: a regular region with an exponential grid spacing that covers the majority of the cell, a narrow and highly refined region where partial concentration functions are steep near the bottom of the cell, and a transition region in between those two regions to ensure a gradual change of the grid spacing. Let N represent the number of radial grid points we wish to use for discretization, and let N_G represent the total number of points used for the entire cell (N_G is slightly larger than N because it includes the points in the adaptive region at the bottom and the transition region). Then define

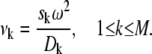Assume furthermore that all ν_k are rearranged in ascending order, i.e.,

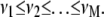Similarly to Cao and Demeler (2), let r*_k be the point at which the steady-state solution of the kth component assumes a threshold value 1/N. We consider [r*_k, b] to be the steep region for the k^th component. It can be verified that

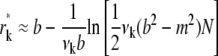(see Cao and Demeler (2) for details). It follows that

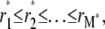and [r*₁, b] covers the steep regions for all components. This region requires a highly refined grid. To determine the grid distribution in this region, we follow the same criterion used for the ASTFEM in Cao and Demeler (2): the local Pèclet number in each [r*_k, b] should be <1. This implies that in each interval [r*_k, b] the step size should be smaller than

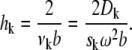Furthermore, we require that the grid spacing decreases from left to right. To satisfy these requirements, we use the sine function to determine the grids in the steep region [r_M*, b]. Let

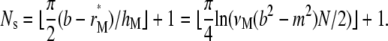We place N_s points in [r*_M, b] as

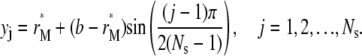The grid spacing in this region can be found as

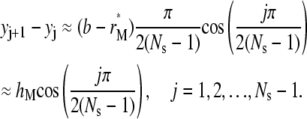Therefore, the spacing decreases gradually as j increases. The leftmost interval is approximately of size h_M, while the rightmost interval is approximately of size 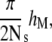which is one order of N_s smaller than h_M.

Now we determine the grid distribution in [r*_k, r*_k+1] for 1 ≤ k ≤ M – 1. Let N_k be a positive integer. Suppose we wish to place N_k subintervals in [r*_k, r*_k+1], with their sizes decreasing arithmetically from h_k at the left-hand side to h_k+1 at the right-hand side. This implies that the element sizes are

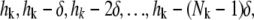where δ is an undetermined number. Because the sum of all the N_k subintervals is equal to r*_k+1 – r*_k, we have

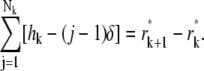Also, the size of the rightmost subinterval equals h_k+1, which implies that h_k – (N_k – 1)δ = h_k+1. Solving for N_k and δ from the above two equations, we obtain

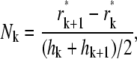and

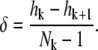The coordinates for the radial points in the subsection [r_k*, r*_k+1] of the steep region are given by

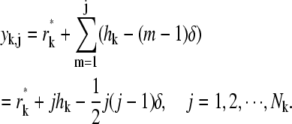Next we determine the grid in the regular and transition regions. We consider (m, r_o) as the regular region and (r_o, r*₁) as the transition region, where

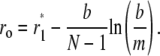Analogously to the literature (2,6), the grid positions in the regular region are chosen to be

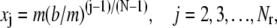(14)

with

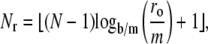and the grid points in the transition region are given by

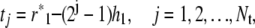with

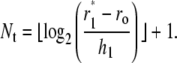Finally, the grids over the entire cell are composed of all the points x_j in the regular region, all t_j in the transition region, and all y_k,j and y_j in the steep region, determined in the above formulas (see Fig. 2). The total number of points is

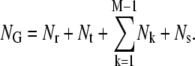This number is typically bigger than N by, at most, a small percentage (<10%); refer to Table 1 in Cao and Demeler (2).

FIGURE 2.

A schematic view of the adaptive radial grid distribution for the regular, transition, and steep regions.

Grids for test functions

In this section, we determine the coordinates 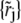used for defining the test functions for each of the Lamm equations (Eq. 2) in Stage 1. Recall that these points should be selected such that the line through 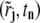and (r_j+1, t_n+1/2) follows approximately the characteristic lines. Thus we choose 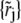according to {r_j} and the sedimentation speed s_k. To indicate the dependence of each set 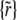on s_k, we use in this section the notation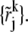

First, we consider the component with the fastest sedimentation speed. Let s_max = max _1≤k≤M s_k be the largest sedimentation coefficient. Let us assume s_max = s_M, then by definition of r_j (Eq. 14) for the regular region, it can be verified that when the time-step size is

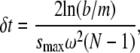(15)

then each grid (r_j, t_n) moving at sedimentation speed s_M according to Eq. 9 will end up exactly at (r_j+1, t_n+1/2). Therefore, we choose 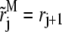for all j in the regular region. In the transition and steep regions, due to the zero flux boundary condition, diffusion transport dominates over sedimentation transport, and diffusion error is much larger than the sedimentation error near the bottom. Thus reducing the sedimentation error by aligning the test function with the characteristic line is not critical. Therefore, we also choose in these two regions 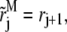even though the line from 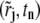to (r_j+1, t_n+1/2) does not follow the characteristic line. Having defined 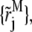the ASTFEM scheme for the fastest component in Eq. 2 is exactly the original ASTFEM for single-component Lamm equations introduced in Cao and Demeler (2).

For other components with s_k < s_max, the above defined 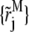is not an appropriate choice for the k^th Lamm equation in Eq. 7, since it has a different characteristic line determined by s_k. For the k^th component, we choose 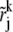by back-tracking (18) (r_j+1, t_n+1/2) at time t_n+1/2 to t_n along its own characteristic line. More precisely, put r(t_n+1/2) = r_j+1 and 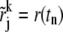into Eq. 9,

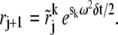We have

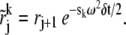By the definition of r_j and δt,

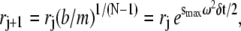hence

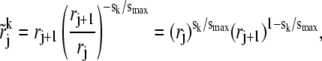i.e., 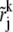is the geometric mean of r_j and r_j+1. For grids in the transition and steep regions, we also use the above formula to determine the coordinates of 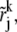even though r_j values are not given by the exponential function in Eq. 14.

Note that by the above definition, each 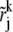lies in between r_j and r_j+1 for all j and k. This ensures that the coefficient matrices A and B in the linear algebraic systems from ASTFEM have, at most, four nonzero diagonal entries.

NUMERICAL RESULTS AND DISCUSSIONS

In this section we present several numerical tests and compare accuracies of our ASTFEM approach and the standard FEM using fixed adaptive meshes (labeled “fam” below). We do not include a comparison with Claverie's method based on fixed uniform grids. Such grids perform significantly worse than ASTFEM which we demonstrated in Cao and Demeler (2). We focus here on differences resulting from sedimentation and diffusion error in the fam solution. In fam, the radial grids are chosen to be 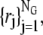the same radial grids as used for ASTFEM. Similar solutions using standard FEM with refined grids near the cell bottom have also been used in Stafford's package Sedanal (5).

We evaluate the solution errors of ASTFEM and the fam methods (both incorporate the same operator splitting scheme) by comparing both solutions to a reference solution c_ref(r, t) obtained by using the fixed grid method with a very large number of grid points (N = 10,000) and small δt values related to N according to Eq. 15.

Since the signal near the meniscus and bottom are routinely excluded from the fit, we consider here only data points that are slightly inside the meniscus and the bottom of the cell (r_m = m + 0.05(b – m) and r_b = b – 0.05(b – m)). We then calculate the L² error (which is equivalent to the square-root-mean error in the discrete case) of the approximate total concentration c between r_m and r_b for the entire simulation process according to

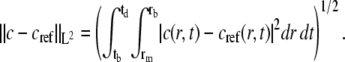The values t_b and t_d are the beginning and end time for the simulation. For all examples, we choose t_d such that the slowest component has essentially reached equilibrium.

For comparison, we consider four different sets of data including monomer-dimer and monomer-trimer associations of small and large molecular weights, and a range of k_off rates. All simulations use a meniscus position of m = 5.8 cm and a bottom position of b = 7.2 cm. All simulations begin at rest from rotor speed 0 accelerated to 60,000 rpm with an acceleration rate of 400 rpm/s. To minimize the influence of the solution error generated in the acceleration stage, we use a fixed adaptive mesh method with twice as many grid points as is used later for steady speed calculation. The mesh is refined in the same way as for ASTFEM near the bottom, and uniformly refined near the meniscus to produce a local mesh density ∼8 times higher than is used in the constant rotor speed stage. In addition, the time-step size is set to be δt = 1 s for the acceleration period. These treatments ensure not only that solution errors reported below are virtually independent of the errors from the acceleration period, but also that the numerical calculation simulates velocity experiments more realistically.

For all the examples it is found that 1), the mass conservation is maintained throughout the entire simulation process to the seventh decimal point; and 2), as indicated by the error analysis of the scheme in Adaptive Grids for ASTFEM of Multicomponent Systems, the solution errors of all numerical solutions (with both ASTFEM and the fixed mesh method) are approximately proportional to N⁻², i.e., when N is doubled, the error is reduced by a factor of 4. This shows that our operator splitting scheme with ASTFEM is second-order convergence in both the space and time variables.

Example 1

In our first example we illustrate the superior accuracy of ASTFEM for solving a two-component noninteracting system where the ratio of sedimentation speed for the two components varies from 0.25 to 0.75. There are two reasons for choosing this test:

1. Noninteracting systems are the limiting cases of interacting systems when k_off approaches zero. Thus conclusions for noninteracting systems hold true for reacting systems with small reaction rates.

2. Our scheme for Eq. 1 is built on the operator splitting method, in which Stages 1 and 3 correspond to solving noninteracting systems. We would like to make sure that these two stages are solved accurately for all components.

The three two-component systems have the following properties (throughout this text sedimentation coefficients are reported in units of seconds (s) diffusion coefficients in units of cm²/s, and k_off rates in units of s⁻¹):

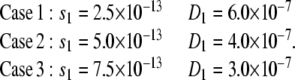(16)

For all cases, the second component is simulated with s₂ = 1.0 × 10⁻¹², D₂ = 2.0 × 10⁻⁷. These systems represent molecules with frictional ratios ranging approximately between 1.6 and 2.1, and molecular weights ranging between 36 and 430 kDa (assuming a partial specific volume of 0.72 ccm/g). The initial partial concentration for both components are set to be 0.5. Simulation times were from time t_b = 150 s to t_d = 17, 676 s.

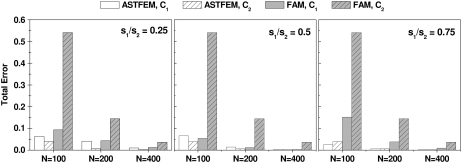
The errors for each component obtained from ASTFEM and fam are shown in Fig. 3. For the fast component C₂, the ASTFEM solution error is between 15 and 22 times smaller than the fam solution error. For the slower component C₁, when s₁/s₂ = 0.75, the ASTFEM solution is much more accurate than the fam solution. For s₁/s₂ = 0.25 and 0.5, both solutions are of similar accuracy. This is understandable since as we demonstrated in Cao and Demeler (2), the adaptive ASTFEM is designed to eliminate the sedimentation errors. It is particularly superior when the sedimentation speed is large or the diffusion coefficient is small. For cases with relatively slow sedimentation or large diffusion, the performance of ASTFEM is similar to the fixed grid methods. Nevertheless, for multicomponent reacting systems, the solution error is determined by the errors in all components. A large error in one component will degrade the accuracy of the entire system. Therefore, for reacting systems, ASTFEM, which is essentially free of sedimentation errors, will always be better or be significantly better than fam. This point is further underscored with the next three examples.

FIGURE 3.

Solution errors for a two-component, noninteracting system comparing ASTFEM and fam for varying ratios of s₁/s₂. Simulation conditions are described in the text in Example 1. Simulations are repeated with N = 100, N = 200, and N = 400 radial data points. ASTFEM outperforms the fam solution for both components, and is virtually independent of s.

Example 2

In the second example, we evaluate the accuracy of a reversible monomer-dimer self-association system. In this example, simulations were performed from time t_b = 150 s to t_d = 8, 587 s, and the sedimentation and diffusion coefficients are given by

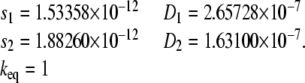(17)

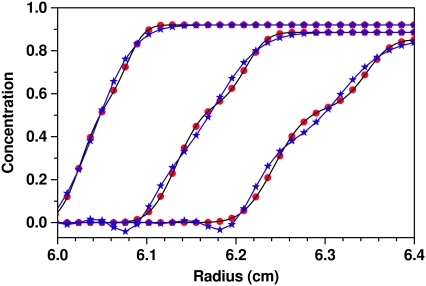
This is a typical case where ASTFEM significantly outperforms the classical fixed mesh methods. Fig. 4 displays the typical solutions obtained with ASTFEM and fam method. Similar to the improvement achieved by the moving hat method and ASTFEM for a single-component Lamm equation (2,6), here ASTFEM captures very well the sedimentation boundaries for finite reacting systems. In contrast, the fixed mesh method introduces significant discretization errors in approximating the sedimentation terms. These errors are responsible for the distortion of the solution boundaries and the oscillation around the boundaries (see Fig. 4).

FIGURE 4.

Comparison of solution accuracy between ASTFEM (red dots) and fam (blue stars) to a high-density reference solution with N = 10,000 (black line) for the system described in the text in Example 2. Shown here is the solution for the case k_off = 10⁻⁴ at times t = 732 s, 1023 s, and 1314 s. In addition to significant deviations in the boundary shape, oscillations are apparent near the baseline for fam, while the ASTFEM solution faithfully reproduces the high-density reference solution.

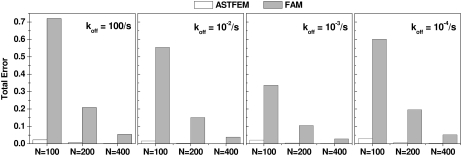
Fig. 5 compares the solution errors for ASTFEM and fam for this example. In this case, the solution accuracy for ASTFEM with only N = 100 is still better than that of fam with as many as N = 400 radial points. In addition, it can be seen that the advantage of ASTFEM is maintained for the entire spectrum of the k_off rates ranging from noninteracting to instantaneous association.

FIGURE 5.

Comparison of ASTFEM and fam solutions to a high-density reference solution with N = 10,000 for a monomer dimer system with a relatively large molecular weight (simulation conditions described in the text in Example 2). The total solution error for simulations with N = 100, N = 200, and N = 400 radial data points for four different k_off rates ranging from instantaneous reactions to almost noninteracting are shown. In this case, ASTFEM offers dramatic accuracy improvements over fam.

Example 3

In this example, we evaluate the accuracy of our solution for the case of a relatively small, globular protein undergoing a monomer-dimer reaction, with monomer molecular weight of 50 kDa and frictional ratio of 1.25. The monomer and dimer solute parameters are given by

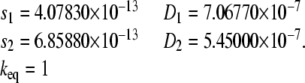(18)

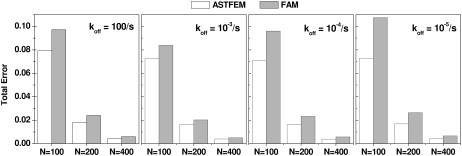
Simulations were performed at 60,000 rpm and scan times between t_b = 150 s and t_d = 18, 516 s were evaluated. In this case, due to a relatively small sedimentation and relatively large diffusion transport, the discretization error originating from the diffusion term is more prominent than the error originating from the sedimentation term. Even though a consistent improvement in the solution is present for all compared conditions, the reduction of the sedimentation errors achieved by ASTFEM is not as striking as for cases where molecular weights are larger. The results for a comparison between ASTFEM and fam against a high-density reference solution with N = 10,000 is shown in Fig. 6.

FIGURE 6.

Comparison of ASTFEM and fam solutions to a high-density reference solution with N = 10,000 for a small molecular weight monomer-dimer system (simulation conditions for Example 3 described in text). The total solution error for simulations with N = 100, N = 200, and N = 400 radial data points for four different k_off rates ranging from instantaneous reactions to almost noninteracting for this system are shown. For a small molecular weight system ASTFEM offers moderate, but consistent accuracy improvements over fam.

Example 4

In the last example, we test a reversible monomer-trimer association system with the same monomer molecular weight as shown in Example 3. The parameters for the system are given by

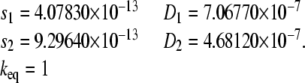(19)

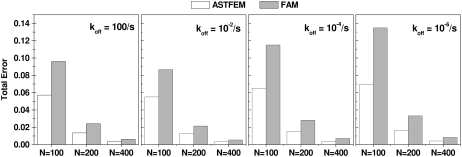
The results are similar to the case of the monomer-dimer association in Example 3, and the ASTFEM solution offers accuracy improvements over fixed mesh methods. The improvements are larger than in the monomer-dimer case which is due to the larger sedimentation speed of the trimer. The results are presented in Fig. 7.

FIGURE 7.

Comparison of ASTFEM and fam solutions to a high-density reference solution with N = 10,000 for a monomer-trimer system (simulation conditions are described in text for Example 4). The total solution error for simulations with N = 100, N = 200, and N = 400 radial data points for four different k_off rates ranging from instantaneous reactions to almost noninteracting for this system are shown. For a small molecular weight system ASTFEM offers moderate, but consistent accuracy improvements over fam.

CONCLUSION

We have presented an ASTFEM solution of the Lamm equation for the general case of interacting and noninteracting solutes. Our approach can be used to model self- or heteroassociating solutes for situations where the reaction is either kinetically limited or where the reaction occurs instantaneously on the timescale of the sedimentation experiment. The ASTFEM solution is of second-order accuracy, i.e., when the number of radial grid points is doubled, the accuracy is increased by a factor of 4, and automatically guarantees mass conservation. By comparing our adaptive solution to the classical FEMs employed by others, we show that an adaptive solution provides superior accuracy, especially for cases where the components are large and the sedimentation speed is relatively high. Because of the use of adaptive radial grids near the bottom of the cell, we can avoid oscillations in the solution around the cell bottom that are observed with FEMs based on uniform meshes without introducing significant computational overhead. In addition, our approach offers several targets for parallelization, improving execution time without sacrificing accuracy of the solution. By modulating the rate constants describing each reaction, it is possible to model any system that falls between the extremes of instantaneous reaction and independent, noninteracting components. As a result, our work will contribute to the analysis of interacting systems by providing more efficient and accurate solutions to the transport equations, and hence allow the investigator to retrieve more reliable parameters when fitting experimental data. This will expand the range of applicability of analytical ultracentrifugation beyond simple noninteracting systems, and open the way to retrieving equilibrium constants and slow reaction kinetics from velocity experiments in a robust fitting environment.

We should note that we have so far only presented a means for accurately modeling a general multicomponent system of arbitrary reactions, but have not proposed a way to solve the inverse problem of fitting such complex models to experimental data. Further work needs to be done to identify conditions under which parameters can be reliably extracted from experimental data. We expect that gradient-based optimization approaches will yield unsatisfactory convergence properties due to irregular error surfaces, and that multidimensional linearizations or stochastic optimization methods proposed earlier (10,11,13) will need to be employed. This will be the subject of future investigations. A graphical user interface to the ASTFEM solution for the simulation of interacting systems, including source code, is available as part of the UltraScan software package (23).