Coupling between ATP Binding and DNA Cleavage by DNA Topoisomerase II

Abstract

DNA topoisomerase II is a molecular machine that couples ATP hydrolysis to the transport of one DNA segment through a transient break in another segment. To learn about the energetic connectivity that underlies this coupling, we investigated how the ATPase domains exert control over DNA cleavage. We dissected the DNA cleavage reaction by measuring rate and equilibrium constants for the individual reaction steps utilizing defined DNA duplexes in the presence and absence of the nonhydrolyzable ATP analog 5′-adenylyl-β,γ-imidodiphosphate (AMPPNP). Our results revealed the existence of two enzyme conformations whose relative abundance is sensitive to the presence of nucleotides. The predominant species in the absence of nucleotides binds DNA at a diffusion limited rate but cannot efficiently cleave DNA. In the presence of AMPPNP, most of the enzyme is converted to a state in which DNA binding and release is extremely slow but which allows DNA cleavage. A minimal kinetic and thermodynamic framework is established that accounts for the cooperativity of cleavage of the two DNA strands in the presence and absence of bound AMPPNP and includes conformational steps revealed in the kinetic studies. The model unifies available kinetic, thermodynamic, and structural data to provide a description for the reaction in terms of the order and rate of individual reaction steps and the physical nature of the species on the reaction path. Furthermore, this reaction framework provides a foundation for a future in-depth analysis of energy transduction by topoisomerase II, for guiding and interpreting future structural studies, and for analyzing the mechanism of drugs that convert topoisomerase into a cellular poison.

Maintaining life requires cells to take up and use energy to perform molecular work. The subcellular devices that accomplish this task have been termed molecular machines, miniature engines that couple a thermodynamically favorable reaction to one that, for thermodynamic or kinetic reasons, would otherwise not take place to a significant extent. Nature has evolved numerous molecular machines that perform vital tasks for the cell in diverse areas, e.g. in force generation, transport of molecules, and synthesis and degradation of nucleic acids and proteins (1–4). Obtaining a molecular level understanding of the mechanism with which these machines take up energy and convert it to perform work is a major goal in biology. An in-depth mechanistic knowledge of their working mechanism can lead to useful clinical applications, as many of these machines are implicated in disease.

Although there have been great strides in obtaining structural descriptions of these machines in recent years, kinetic and thermodynamic descriptions of individual reaction steps, the other critical component of mechanistic understanding, are lacking in many cases. Here we investigate aspects of energy conversion in DNA topoisomerase II, a molecular machine that simplifies DNA topology during replication, transcription, recombination, chromosome segregation, and chromosome condensation (4).

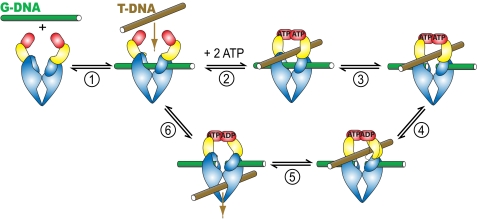
Topoisomerase II alters DNA topology by allowing DNA chains to freely pass through each other (5). Biochemical and structural studies have suggested a mechanism for the overall action of topoisomerase II (Fig. 1) (6, 7). The enzyme binds two DNA segments. One DNA segment is bound to the DNA cleavage domain and is termed the gated or G-DNA segment. Another segment, termed the transported or T-segment, binds and is trapped inside the enzyme when ATP binding induces a conformational change that clamps the ATPase domains around it. The enzyme introduces a transient double strand break in the G-DNA using two active site tyrosines that covalently attach to a 5′-phosphoryl group on each DNA strand. This break widens and acts as a gate through which the T-segment DNA is transported. The double strand break in the G-DNA is religated, and the transported segment is released from the enzyme. The DNA transport reaction is coupled to the hydrolysis of ATP (8, 9). The ATPase reaction therefore regulates or powers steps in the reaction cycle in a way that allows the complex DNA transport reaction to take place efficiently. Elucidating the mechanism whereby the energy from hydrolysis of ATP is garnered to control or fuel other reaction steps is a major goal in topoisomerase research and in the field of molecular machines in general.

FIGURE 1.

Model of the topoisomerase II-catalyzed DNA transport reaction. Individual steps are described in the Introduction and under “Results and Discussion.” ATP binding (GHKL) domains are colored red, transducer domains yellow, DNA cleavage domains blue, G-DNA green, and T-DNA brown.

Aspects of the energetic coupling between the ATPase reaction and other steps during the reaction cycle of topoisomerase II have emerged over the past decades. It is well established from an array of diverse biochemical and structural studies that binding of ATP and ATP analogs is coupled to dimerization of isolated ATP binding domains (10–21). In the context of the full-length enzyme, the dimerized ATPase domains form a molecular clamp, enabling them to enclose and topologically trap a T-DNA segment (11, 22). Thus, the binding energy of ATP is apparently employed to help capture a T-DNA segment. ATP hydrolysis also has important mechanistic functions for the catalytic cycle of topoisomerase II. First, ATP hydrolysis ensures that the clamp formed by the ATPase domains upon ATP binding reopens to allow another T-DNA segment to enter the enzyme (23). Moreover, Lindsley and co-workers (9, 24, 25) elegantly demonstrated in rapid quench and pulse-chase kinetic experiments that the two ATP molecules bound to the ATPase domains are sequentially hydrolyzed and that hydrolysis of the first ATP accelerates DNA transport.

Nucleotide binding is sensed not only locally within the ATPase domains but also globally in remote regions of the enzyme. It has been recognized for more than 2 decades that nucleotide binding can elevate the extent of topoisomerase-mediated DNA cleavage, demonstrating energetic cross-talk between the ATPase and DNA cleavage domains (8, 26, 27).

Lindsley and co-workers (9, 24, 25) elegantly analyzed the steps in the ATP hydrolysis cycles, but it remains to be elucidated how these steps integrate with the steps involved in the DNA cleavage and religation reaction. Here we mechanistically dissect the DNA cleavage reaction, and furthermore, we unite our kinetic and thermodynamic reaction framework with the existing structural data to provide a detailed working model for the interconnection between DNA binding and cleavage and the binding of ATP. This model implicates the ATPase domains as strict regulators of DNA cleavage and suggests that gate closure provides an on/off switch for cleavage of both DNA strands. These results and those of Lindsley and co-workers (9, 24, 25) lay a foundation for future dissection of the integrated workings of the DNA cleavage and ATPase apparatus of this molecular machine.

EXPERIMENTAL PROCEDURES

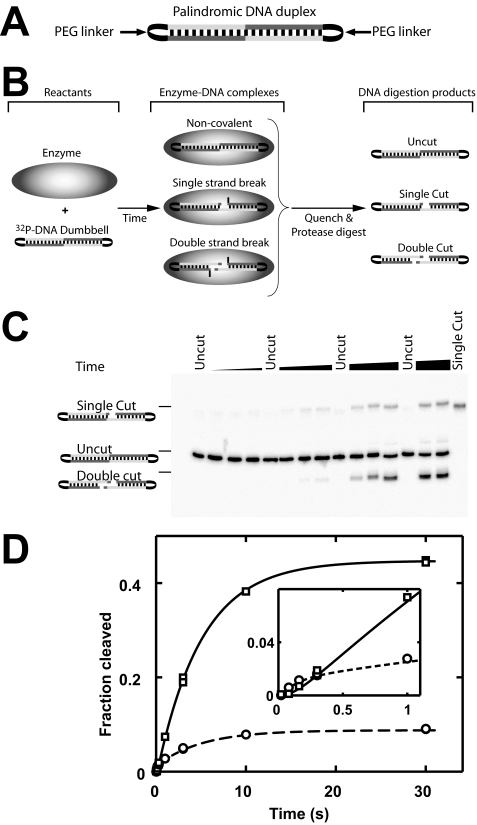
Oligodeoxyribonucleotides and DNA Duplexes—A previously characterized 40-bp DNA duplex containing a strong topoisomerase II cleavage site (28) served as the basis for the DNA duplexes used herein (see supplemental Table S1). For fluorescence anisotropy measurements, this 40-bp duplex carried the fluorescent dye ROX3 covalently attached to one of the two 5′ termini (supplemental Table S1). We also created a DNA palindrome based on the cleavage site within the 40-bp duplex. The length of the duplex was reduced to 34 bp to position the DNA cleavage site in the center of the duplex. The cleavage specificity of the main cleavage site of this 34-bp duplex was >95% (supplemental Fig. S7). A “DNA dumbbell” was created from this 34-bp palindromic duplex by covalently connecting the 3′- and 5′-ends of opposing strands via triethylene glycol linkers (Fig. 4A). DNA duplexes whose termini were not connected by a linker are referred to as blunt-ended duplexes. A protocol for assembly and purification of the duplexes is provided in the supplemental material.

FIGURE 4.

DNA cleavage of dumbbell DNA mediated by nucleotide-free enzyme. A, schematic of the palindromic DNA dumbbell used as a cleavage substrate. The 5′- and 3′-ends of the duplex are covalently connected by triethylene glycol linkers (PEG). B, work flow of the DNA cleavage assay. Upon mixing of enzyme and ³²P-labeled DNA, the specified covalent and noncovalent enzyme-DNA complexes are formed. After quenching the reaction mixture, the DNA was liberated from the covalent enzyme-DNA complexes by protease digestion before the mixture was separated by denaturing PAGE. C, cleavage time course of 1 nm dumbbell DNA using 900 nm enzyme. Uncut dumbbell DNA and pure single cut DNA were loaded as controls. D, quantification of the gel shown in C. Single strand breaks, circles; double strand breaks, squares. Time courses obtained with a 3-fold lower enzyme concentration gave results that were the same within 10%, indicating that saturating enzyme concentrations were used (supplemental Fig. S8). Lines represent a global fit of the time courses to Scheme 1. Estimates for individual rate constants are summarized in Table 2.

The dumbbell DNA duplex is cleaved to a slightly lesser extent at equilibrium with saturating concentrations of enzyme present than a blunt-end DNA duplex of the same sequence. The supplemental material discusses possible reasons for this discrepancy. The likeliest model is that a fraction of the DNA dumbbell (10%) assumes an alternative (secondary) structure that renders it uncleavable by topoisomerase II. The fraction of cleavable DNA dumbbell duplex is therefore corrected for this fraction in the quantitative analysis of the DNA cleavage reaction.

Enzyme Assays—Saccharomyces cerevisiae DNA topoisomerase II was purified as described (29). Reaction buffer (50 mm potassium HEPES, pH 7.5, 150 mm KOAc, 0.1 mm Na-EDTA, 20% sucrose, 0.25 mg/ml bovine serum albumin, 0.01% Tween 20, 5 mm 2-mercaptoethanol and 10 mm Mg(OAc)₂ or Ca(OAc)₂) was employed throughout (29). All enzyme assays were performed at 30 °C. All results were independently replicated. In all cases the replicates agreed well, with observed rate constants varying by no more than 2-fold.

The reaction buffer was supplemented as indicated with 0.5 mm AMPPNP (Sigma). Variation of the AMPPNP concentration between 0.1 and 1.2 mm did not change the observed DNA binding, release, and cleavage kinetics, indicating saturation of AMPPNP (data not shown). Saturation of AMPPNP in these experiments was independently confirmed by determining the apparent affinity for AMPPNP. By measuring cleavage of subsaturating concentrations of a ³²P-labeled DNA duplex at equilibrium over a range of AMPPNP and enzyme concentrations, we determined apparent affinities for AMPPNP of <25 μm for the free enzyme, the noncovalent and the covalent enzyme-DNA species (data not shown). AMPPNP was purified as described (30) except when used in stopped flow fluorescence anisotropy experiments. Identical DNA binding and dissociation kinetic traces were obtained using purified and unpurified AMPPNP in control stopped flow fluorescence anisotropy experiments.

Stopped Flow Fluorescence Anisotropy Measurements—DNA binding and release of the ROX-labeled 40-bp DNA duplex was followed by fluorescence anisotropy using an Applied Photophysics SX.18MV stopped flow spectrofluorimeter. The presence of the fluorophore has only a small effect (<2-fold) on the DNA affinity (29). An excitation wavelength (548 nm) was selected with a monochromator using an optical slit width of 14 nm, and emission was observed through 590 nm long pass filters (CVI). DNA binding was followed by mixing equal volumes of enzyme and ROX-labeled 40-bp DNA at the indicated concentrations. DNA dissociation was monitored in pulse-chase experiments in which a complex between enzyme and ROX-labeled DNA was allowed to form for a specified amount of time before the reaction was “chased” with excess unlabeled sheared fish sperm DNA (Eppendorf). Control experiments identified no difference in DNA dissociation traces if the DNA concentration of the chase was varied 5-fold or if a 40-bp DNA duplex was used as a chase (data not shown). Before and after each experiment the base-line fluorescence anisotropy was determined by either mixing dye-labeled DNA with buffer (for DNA binding experiments) or by mixing the preformed enzyme-dye-labeled DNA complex with buffer (for DNA dissociation experiments). For presentation purposes, the data are smoothed using a moving average filter with a window of 21 data points.

Quantitative Analysis of Stopped Flow Fluorescence Anisotropy Measurements—DNA binding kinetic traces were first fit to a single, double, or a triple exponential expression (Equations 1, 2, 3) as specified.

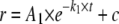(Eq. 1)

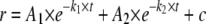(Eq. 2)

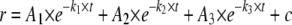(Eq. 3)

Analysis of the best fit values suggested minimal models for the DNA binding and dissociation data (supplemental Schemes S1 and S2; see “Results” and “Discussion”). Through kinetic modeling of the reactions according to supplemental Schemes S1 and S2 in Simulink (The Mathworks) and global fitting of the binding or dissociation reactions in Matlab (The Mathworks), we extracted individual rate constants. The two enzyme-DNA species E_SS and E′ in supplemental Schemes S1 and S2 were assigned the same fluorescence anisotropy in the fits.

Transient Kinetic Measurements of DNA Cleavage and Religation—DNA cleavage reactions that used the 40-bp DNA duplex (supplemental Table S1) were carried out as follows. For reactions with observed rate constants below 0.1 s^-1, the indicated concentrations of enzyme and ³²P-labeled DNA, both pre-equilibrated at 30 °C, were mixed together. Aliquots from the reaction mixture were removed, and the reaction was quenched with 2 volumes of 1 m NaOH. Reactions with an observed rate constant of >0.1 s^-1 were measured using the KinTek RQF-3 rapid quench apparatus with 2 m NaOH in the quench line. Control experiments showed that higher NaOH concentrations (6 m) as the quench solution gave indistinguishable results.

DNA religation of the ³²P-labeled 40-bp duplex was measured in pulse-chase experiments. Topoisomerase II was first pre-equilibrated with trace amounts of the ³²P-labeled DNA duplex before the reaction mixture was chased with excess concentrations of unlabeled sheared fish sperm DNA. Control experiments showed that a dilution chase in place of the unlabeled DNA chase results in indistinguishable DNA religation kinetics (not shown). Cleavage and religation reactions using the 40-bp duplex were analyzed as described (29).

The DNA cleavage and religation kinetics of the 34-bp DNA dumbbell were measured with the rapid quench apparatus as above. The quenched reaction mixtures were titrated to pH 9 with concentrated Tris-HCl, pH 7, that was present in the sample collection tubes. Proteinase K (1 mg/ml; U. S. Biochemical Corp.) was added to digest protein covalently linked to the DNA. After incubating the mixture for 1 h at room temperature, the mixture was diluted with 3 volumes of 8 m urea, 20% sucrose, 5 mm Na-EDTA. Denaturing PAGE (14%, 9 m urea, temperature controlled at 42 °C) was used to separate reactants and cleavage products.

Quantitative Analysis of the Pre-steady State DNA Cleavage Data—Rate and equilibrium constants were determined from DNA cleavage time courses by globally fitting the time courses for formation of the single and double strand breaks to Scheme 2A. To this end a kinetic model describing the scheme was constructed in Simulink, and a global fitting routine using a nonlinear least squares algorithm was implemented in Matlab.

SCHEME 2.

RESULTS AND DISCUSSION

We recently identified reaction conditions that prevent the transported segment DNA from binding, yet allow measurement of DNA cleavage, DNA religation, and the coupling between DNA cleavage and nucleotide binding (29) (Fig. 1). Selective occupancy of the G-DNA-binding site is accomplished using DNA duplexes that are not long enough to contact both binding sites simultaneously and by using enzyme in excess of DNA (29). We have previously shown that the occupancy of the T-DNA-binding site has at most a modest influence on cleavage of the G-DNA (29). These reaction conditions greatly reduce the complexity of the topoisomerase-mediated DNA cleavage reaction. We further used a novel symmetrical, cyclic DNA “dumbbell” substrate (Fig. 4A, below) that allowed us to unambiguously distinguish the first and second DNA cleavage steps. With these tools in hand, we were able to dissect the individual reaction steps that allow the ATPase domains to exert control over the DNA cleavage reaction.

To unravel the communication between the ATPase and DNA cleavage domains, we mechanistically dissected the DNA cleavage reaction by establishing the sequence, rate, and equilibrium constants of individual reaction steps for the nucleotide-free enzyme and the enzyme with a bound nonhydrolyzable ATP analog. The results have led us to formulate a unifying mechanism for the coupling between nucleotide binding and DNA cleavage by DNA topoisomerase II that brings together available structural, thermodynamic, and kinetic data.

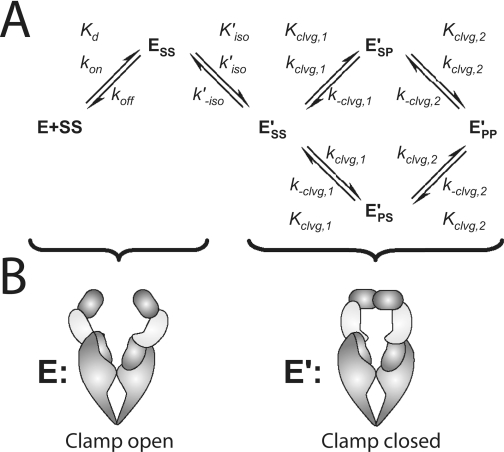
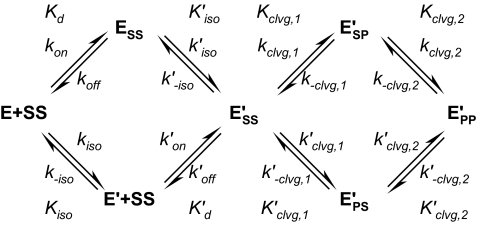
The minimal reaction scheme that can account for all the data presented below is summarized in Scheme 1. The enzyme can exist in two conformations, E and E′. Both conformations can have G-DNA bound. The G-DNA is termed SS in the scheme where the first and second S designate the top and bottom strand of the DNA in the uncleaved “substrate” form. Only the E′ species can cleave DNA. Either one of the two strands can be cleaved first, generating two species with one of the two strands in the product state (E_SP′ or E_PS′), before the second strand is cleaved to form E_PP′. We first present experiments that define rate and equilibrium constants in the scheme in the absence of nucleotides and then measure how the framework responds to the binding of AMPPNP.

SCHEME 1.

Topoisomerase II-mediated DNA cleavage is dependent on divalent metal ions. In the presence of the physiological Mg²⁺ ions, very little DNA cleavage is observed (8, 29, 31). This low signal is a major obstacle to a thorough quantitative analysis. Ca²⁺ in place of Mg²⁺ has been found to stimulate topoisomerase II-mediated DNA cleavage (32) and has therefore been extensively exploited to increase the signal in DNA cleavage assays (see for example Refs. 8, 28, 29, 33, 34). Here, we also used Ca²⁺ to enhance the DNA cleavage signal. In DNA binding and dissociation experiments we have employed Mg²⁺ as well as Ca²⁺ to control for potential effects from DNA cleavage and to compare the effects of the two divalent metal ions. In all cases the results with Ca²⁺ and Mg²⁺ are analogous.

A Thermodynamic and Kinetic Framework for DNA Cleavage by the Nucleotide-free Enzyme

DNA Binding and Release: Evidence for Two Enzyme-DNA Species—Binding of DNA to topoisomerase II can be followed by fluorescence anisotropy (29). The DNA duplex is covalently labeled with a fluorophore, and the fluorescence anisotropy increases upon protein binding. We previously used this assay to follow equilibrium DNA binding. Here we determine the time dependence of DNA association and dissociation using stopped flow fluorescence anisotropy to extract kinetic information. The data define rate constants for the association and dissociation rate constants. The time traces in both Mg²⁺ and Ca²⁺ possess multiple phases, providing evidence for a multiple noncovalent enzyme-DNA species. Evidence for the covalent enzyme-DNA complex was also obtained in the kinetic traces in Ca²⁺ but not in Mg²⁺, as only Ca²⁺ permits DNA cleavage to take place.

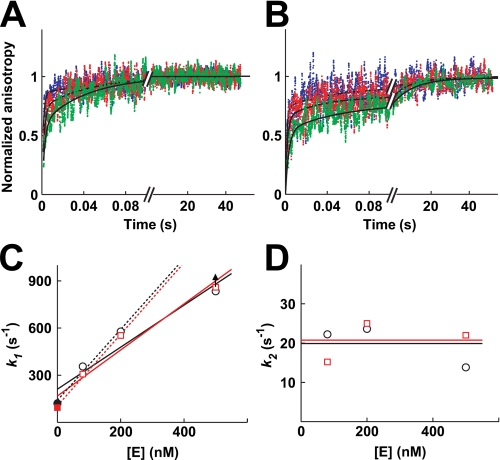
The association kinetics between DNA and varying enzyme concentrations in the presence of Mg²⁺ and Ca²⁺ is shown in Fig. 2, A and B, respectively. Two kinetic phases are observed in Mg²⁺ and three in Ca²⁺. The observed rate constant describing the fastest phase increases with increasing enzyme concentrations (Fig. 2C) as expected for an association, i.e. a second-order reaction. An association rate constant of k_on = 10⁹ m^-1 s^-1 is obtained in Mg²⁺ and Ca²⁺ through a fit of the time courses to the minimal mechanism (supplemental Fig. S2, Table 1; see also “Experimental Procedures”). The magnitude of the association rate constant suggests that DNA binding is essentially encounter-limited (35).

FIGURE 2.

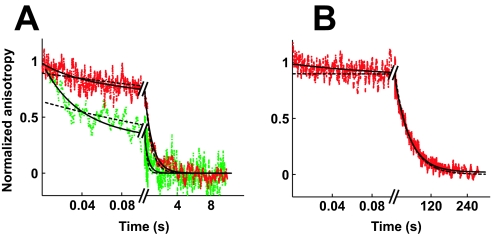
Binding of DNA to nucleotide-free enzyme. The association of enzyme and DNA was measured by rapidly mixing fluorophore-labeled DNA with enzyme and following the increase of the anisotropy over time by stopped flow fluorescence anisotropy in Mg²⁺ (A) and Ca²⁺ (B). The individual binding reactions were repeated 8–18 times and the data averaged. A, final concentrations used were 80 nm fluorophore-labeled DNA with 80 nm (green), 200 nm (red) or 500 nm (blue) enzyme. The data in Mg²⁺ (A) were fit to a double exponential expression (Equation 2; solid lines), giving best fit values k₁ = 350 s^-1, A₁ = 0.61, k₂ = 22 s^-1, A₂ = 0.39 (green); k₁ = 580 s^-1, A₁ = 0.72, k₂ = 24 s^-1, A₂ = 0.28 (red); k₁ = 830 s^-1, A₁ = 0.86, k₂ = 14 s^-1, A₂ = 0.14 (blue). The kinetic traces in Ca²⁺ (B) were fit to a triple exponential expression (Equation 3; solid lines). Best fit values are as follows: k₁ = 310 s^-1, A₁ = 0.55, k₂ = 15 s^-1, A₂ = 0.24, k₃ = 0.07 s^-1, A₃ = 0.20 (green); k₁ = 550 s^-1, A₁ = 0.67, k₂ = 25 s^-1, A₂ = 0.17, k₃ = 0.1 s^-1, A₃ = 0.15 (red); k₁ = 890 s^-1, A₁ = 0.73, k₂ = 14 s^-1, A₂ = 0.18, k₃ = 0.04 s^-1, A₃ = 0.09 (blue). C, value of k₁ depends linearly on the enzyme concentration in Mg²⁺ (circles) and Ca²⁺ (squares). Values for k₁ are taken from A and B (open symbols). In addition, k₁ in the absence of enzyme is approximated by the observed dissociation rate constant (closed symbols; Fig. 3). The data were fit with a line of slope 1.3 ^* 10⁹ m^-1 s^-1 (Mg²⁺) and 1.5 ^* 10⁹ m^-1 s^-1 (Ca²⁺). The value for k₁ at the highest enzyme concentration may represent a lower limit (arrow) because of dead time of the instrument for mixing. Omitting these data points from the fits, the slopes of both lines increase to 2.3 ^* 10⁹ m^-1 s^-1 (dashed lines). D, value of k₂ is independent of the enzyme concentration. Lines indicate the mean. Symbols as in C.

TABLE 1.

Kinetic parameters determined from DNA association and dissociation kinetic data in Mg²⁺ Rate constants are defined in Scheme 1 and obtained from fits shown in supplemental Figs. S2 and S3.

Rate constant	Nucleotide-free state	AMPPNP bound state
kon	109m–1 s–1	109m–1 s–1
koff	120 s–1	20 s–1
k′on	NDa	<1 × 106m–1 s–1
k′off	ND	<1.5 s–1
kiso	ND	0.12 s–1
k–iso	ND	0.035 s–1
k′iso	7 s–1	5.3 s–1
k′–iso	9 s–1	1.5 s–1

^aND means not determined

The DNA association kinetic traces possess a second phase with an average rate constant of 20 ± 6 s^-1 in Mg²⁺ and 21 ± 5 s^-1 in Ca²⁺. The lack of a concentration dependence for this phase (Fig. 2D) indicates that a first-order process, such as a conformational rearrangement, is responsible. This step could take place prior to or after formation of the enzyme-DNA complex. The DNA dissociation kinetics in Mg²⁺ shown below provide evidence for a conformational rearrangement that follows binding of DNA. Thus, the simplest model to account for the association and dissociation data includes binding of DNA (K_d, supplemental Scheme S1) and a conformational change of the enzyme-DNA complex (K′_iso). The DNA association and dissociation data can be quantitatively fit by such a simple model (supplemental Fig. S2 and Table 1).

Because DNA cleavage occurs efficiently in Ca²⁺ (∼50% of the DNA is cleaved at equilibrium with saturating enzyme concentrations; supplemental Fig. S1) but not in Mg²⁺ (<1%) (29), we expected to observe an additional phase in the DNA binding kinetics that occurs on the same time scale as DNA cleavage. A third phase in the association time traces is indeed observed in Ca²⁺ but not in Mg²⁺ and has a rate constant of 0.07 ± 0.02 s^-1 (Fig. 2). This rate constant is the same within error as the observed rate constant for cleavage of a DNA duplex that shares the same nucleotide sequence but lacks the fluorophore under otherwise identical conditions (k_obs = 0.08 ± 0.01 s^-1; supplemental Fig. S1A). This phase of the DNA binding traces is therefore assigned to DNA cleavage.

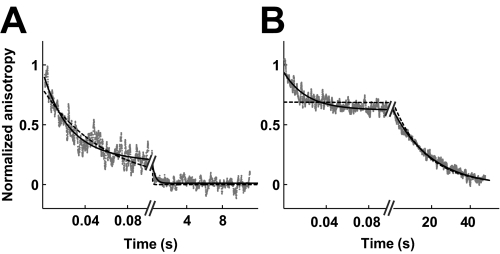
DNA dissociation from nucleotide-free enzyme is also complex, occurring in two phases in both Mg²⁺ and Ca²⁺ (Fig. 3, A and B). The faster phase (k₁ = 120 s^-1 in Mg²⁺ and 90 s^-1 in Ca²⁺) is assigned to DNA dissociation. The calculated K_d = k_off/k_on = 120 s^-1/10⁹ m^-1 s^-1 = 120 nm in Mg²⁺ is 2-fold larger than the value of 60 nm determined by equilibrium binding experiments under the same conditions (29). The 2-fold difference may be caused by the significant noise in the fluorescence anisotropy data. Alternatively, the previously unrecognized existence of an isomerization step subsequent to DNA binding (see below) can also account for the small discrepancy.

FIGURE 3.

Dissociation of DNA from nucleotide-free enzyme. Dissociation of enzyme and DNA was followed by stopped flow fluorescence anisotropy in Mg²⁺ (A) and Ca²⁺ (B). The enzyme and fluorophore-labeled 40-bp DNA were first equilibrated at the given concentrations to allow them to associate before the mixture was chased with excess unlabeled DNA. Data from four (A) and seven (B) separate injections were averaged. A, mixture of enzyme (900 nm) and fluorophore-labeled DNA (500 nm) was chased with excess unlabeled DNA. Solid line, double exponential fit (Equation 2; k₁ = 120 s^-1; A₁ = 0.56; k₂ = 9 s^-1; A₂ = 0.44). The use of a double exponential instead of a single exponential to describe the data is statistically warranted (p < 2 × 10^-4; f test). B, mixture of enzyme (600 nm) and fluorophore-labeled DNA (300 nm) was chased with excess unlabeled DNA. Solid line, double exponential fit (Equation 2; k₁ = 90 s^-1; A₁ = 0.3; k₂ = 0.055 s^-1; A₂ = 0.7). Dashed black lines, single exponential fits for comparison.

The presence of a second phase in DNA dissociation time traces obtained in the presence of Mg²⁺ and Ca²⁺ indicates that two enzyme-DNA species exist under these conditions. Indeed, at least two enzyme species are expected in the presence of Ca²⁺, conditions that permit DNA cleavage: the noncovalent and the covalent enzyme-DNA complexes. The faster DNA dissociation phase could represent dissociation of the noncovalent complex, whereas the slower phase could result from rate-limiting religation of the DNA breaks before enzyme and DNA can dissociate. Indeed, the observed rate constant of the second phase (k₂ = 0.055 s^-1) is close to the observed rate constant of DNA religation using a DNA duplex that shares the same nucleotide sequence but lacks the fluorophore (0.05 s^-1; data not shown). Although the amplitude of the slow phase (70%) modestly exceeds the estimated fraction of covalent complexes under these conditions (∼55%), the data are nevertheless consistent with this phase representing DNA religation (supplemental material).

Although DNA religation can account for the slow dissociation phase observed in Ca²⁺, it cannot account for it in the presence of Mg²⁺. In Mg²⁺ the cleavage complex does not appreciably accumulate (<1%) (29). DNA religation would therefore not be expected to be detectable in the DNA dissociation time traces. The presence of a second DNA dissociation phase in Mg²⁺ therefore suggests the accumulation of a second noncovalent enzyme-DNA species. Two noncovalent enzyme-DNA species could build up if the complex between enzyme and DNA can conformationally rearrange (K′_iso; supplemental Scheme S1). Alternatively, two enzyme (or DNA) species could exist that cannot interconvert, for example because they differ covalently (supplemental Scheme S5B). The former model quantitatively fits the DNA association and dissociation data (black lines in supplemental Fig. S2 and Table 1). The latter model cannot explain the presence of a second association phase that lacks a concentration dependence (Fig. 2D).

The results presented in this section provide evidence for a step that follows DNA binding (K′_iso; supplemental Scheme S1). This conclusion is fully consistent with and further supported by results described below. We show in a subsequent section that the enzyme can undergo a conformational change even without a bound DNA (K_iso; Scheme 1). The isomerization step prior to DNA binding is most likely not detected in the data above because one of the two enzyme conformations (E′; Scheme 1) is not strongly populated in the absence of nucleotides (see below).

A Kinetic Dissection of DNA Strand Cleavage: Evidence for Cooperative Cleavage of the First and Second DNA Strands—We continued with the mechanistic dissection of the DNA cleavage reaction catalyzed by the nucleotide-free enzyme using a DNA cleavage assay. With a novel cyclic DNA cleavage substrate, we were able to obtain information about rate constants associated with cleavage of the first and second DNA strand.

The DNA cleavage substrate we employed has two important features. First, it is palindromic with the cleavage site positioned in the center of the molecule (see “Experimental Procedures”). The palindromic nature of the cleavage site makes the two species with a single strand break (E_SP′ and E_PS′) chemically identical. Cleavage and religation of the top and the bottom DNA strand can therefore be described with the same rate constants, i.e. k_clvg,1 = k′_clvg,1, k_-clvg,1 = k′_-clvg,1, k_clvg,2 = k′_clvg,2, and k_-clvg,2 = k′_-clvg,2, and Scheme 1 simplifies to Scheme 2A. Second, the termini of the duplex are covalently linked with triethylene glycol linkers (Fig. 4A; “Experimental Procedures”). With this cyclic DNA dumbbell, the enzyme-DNA species with a single strand break can be distinguished from the species with a double strand break by denaturing PAGE (Fig. 4, B and C). Such a distinction is not possible when conventional blunt-end DNA duplexes are used because both complexes result in the same experimental readout in the DNA cleavage assay (compare supplemental Fig. S7 with Fig. 4C).

The reaction conditions were chosen to further reduce the complexity of the analysis. We showed above that the enzyme exists in two conformations, E and E′ (Scheme 1). In a subsequent section, we demonstrate that only E can rapidly bind DNA. For the DNA cleavage experiments, we used enzyme in large excess of DNA to ensure that enough fast binding enzyme (E) is in solution to quickly bind all DNA substrates. The presence of E′ and the rate constants k_iso, k_-iso, k′_on, and k′_off in Scheme 1 can therefore be neglected (Scheme 2A).

A time course for cleavage of trace concentrations of the ³²P-labeled DNA dumbbell by excess concentrations of nucleotide-free topoisomerase II is shown in Fig. 4, C and D. The formation of the double strand break follows a time lag. This lag is expected because the second strand can only be cleaved after the first strand has been cut. These results also show that the equilibrium levels of the double strand break exceed that of the single strand break (Fig. 4D, end points). Biologically, the low accumulation of enzyme species with a single broken strand can be rationalized. A single strand break does not permit passage of the transported DNA segment. Perhaps evolutionary pressure then minimized accumulation of this intermediate as it represents a covalent and thus potentially cytotoxic protein-DNA adduct.

Quantitative information about rate and equilibrium constants was extracted by fitting the time courses in Fig. 4D to the minimal model shown in Scheme 2A (Table 2). The DNA cleavage assay directly monitors the changes in the concentration of the covalent enzyme-DNA complexes E_SP′, E_PS′, and E_PP′. Cleavage at equilibrium thus directly defines the second cleavage equilibrium constant K_clvg,2, and we can obtain values for the underlying rate constants k_clvg,2 and k_-clvg,2 from the kinetic traces. In contrast, the assay does not distinguish the two noncovalently bound enzyme-DNA complexes (E_SS and E_SS′). The rate constants for formation of E_SS′ and the subsequent first cleavage step can therefore not be disentangled, and only limits can be determined without additional constraints on the model. Based on results discussed in subsequent sections, we propose below a minimal mechanism that is fully consistent with all of the experimental results. In this mechanism the observed kinetic and thermodynamic differences between the first and the second chemical steps originate from the isomerization step preceding cleavage of the first strand. The microscopic rate constants for cleavage and religation of the first and second strand are the same in this mechanism (k_clvg,1 = k_clvg,2 and k_-clvg,1 = k_-clvg,2). The DNA cleavage time courses are well fit by this mechanism (Fig. 4D, lines). With these additional constraints, each rate constant in Scheme 2A is defined by a unique value, not only a limit, and those rate constants are given in parentheses in Table 2.

TABLE 2.

Best fit rate and equilibrium constants to the DNA cleavage data Datasets obtained in different nucleotide states from Figs. 4 and 7 were fit separately to supplemental Scheme 2A.

Rate or equilibrium constant	Nucleotide-free state	AMPPNP-bound state
Kclvg,1, obs = Kclvg,1/(1/K′iso + 1)	0.13	0.88
Kclvg,2	9.9	9.7
k′isoa	>0.1 s–1 (1.2 s–1)	>1 s–1 (1.2 s–1)
k′–isoa	>0.1 s–1 (91 s–1)	>0.3 s–1 (12 s–1)
kclvg,1a	>0.1 s–1 (5.7 s–1)	>0.3 s–1 (6.4 s–1)
k–clvg,1a	>0.3 s–1 (0.58 s–1)	>0.3 s–1 (0.66 s–1)
kclvg,2a	6.6 s–1 (5.7 s–1)	6.5 s–1 (6.4 s–1)
k–clvg,2a	0.61 s–1 (0.58 s–1)	0.67 s–1 (0.66 s–1)

^aValues in parentheses were obtained for a model with the additional constraints, k_clvg,1 = k_clvg,2 and k_–clvg,1 = k_–clvg,2

The kinetic and thermodynamic data allow us to draw conclusions about the cooperativity of the two sequential cleavage reactions. Although E_SS and E^′_SS cannot be individually monitored, the sum of the concentrations of these species is obtainable. With the sum of the concentrations of these noncovalent species available, we can calculate an observed equilibrium constant for cleavage of the first strand (K_{clvg,1, obs}; Equation 4).

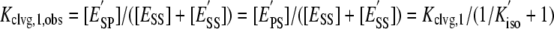(Eq. 4)

Inspection of Table 2 shows that K_{clvg,1, obs} is more than 70-fold smaller than the equilibrium constant for formation of the second cut (K_clvg,2). In other words, the enzyme species that has cleaved one strand is a thermodynamically unstable intermediate that resolves by religating the broken strand or by cleaving also the opposite strand. Cleavage of the two strands is therefore thermodynamically cooperative. Also, the first cut appears with an observed rate constant (k_obs = 0.3 s^-1; supplemental Fig. S8) that is significantly smaller than the rate constant for cleavage of the second strand (k_clvg,2 = 6.6 s^-1; Table 2). Hence, cleavage is fast once one strand is broken, an observation that we refer to as observed kinetic cooperativity.

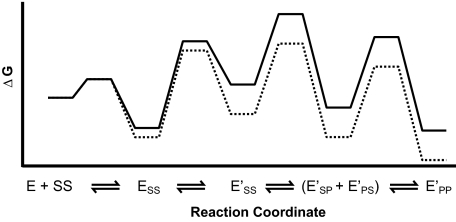
To further test the kinetic and thermodynamic framework derived above, we probed if it can accurately predict the kinetics of the reverse reaction, religation of the DNA strands. Cleavage of the first and the second strand has the same rate-limiting step, formation of the first strand break (see supplemental material). The same must also be true for the reverse reactions, the religation of the broken strands. The enzyme is thus expected to reach equilibrium for the second cleavage step faster than it can religate the cut in the first strand. Furthermore, the ground state for religation of the double and the single strand breaks is the same in the mechanism we derived, as the species E^′_PP is thermodynamically more stable than the species with a cut in a single strand (Fig. 8). For these reasons, the kinetic framework predicts that single and double strand breaks in the DNA are religated with the same observed rate constants.

FIGURE 8.

Free energy profile for the DNA cleavage reaction catalyzed by the nucleotide-free (solid line) and the AMPPNP-bound enzyme (dotted line). Rate constants were taken from supplemental Fig. S6. To better visualize the free energy changes of the different species, all free energy barriers were proportionally shortened by multiplying each rate constant by 10⁹. The standard state is 1 μm enzyme.

We tested this prediction by measuring DNA religation time courses. The enzyme was first allowed to cleave the radiolabeled DNA duplex. Then the reaction was chased with excess unlabeled DNA, and the time dependence of strand religation was followed (supplemental Fig. S5A). As predicted, the observed rate constants for the disappearance of the single and the double strand breaks in the DNA are indistinguishable from one another (k_{obs, single break} = 0.056 s^-1, k_{obs, double break} = 0.048 s^-1). Moreover, the observed rate constants for religating the single and double strand break match within 50% the rate constants predicted based on the minimal kinetic framework we determined above (k_{pred, single break} = k_{pred, double break} = 0.07 s^-1; analysis not shown and supplemental Fig. S5A).

A Thermodynamic and Kinetic Framework for the DNA Cleavage Reaction of the AMPPNP-bound Enzyme

Binding of AMPPNP Induces an Enzyme Conformation Characterized by Hindered DNA Binding and Release—In the next sections, we describe studies of DNA binding, release, and cleavage in the presence of the nonhydrolyzable ATP analog AMPPNP to examine its effect on the DNA cleavage reaction. We start with a characterization of DNA binding and release in Mg²⁺ and Ca²⁺ using enzyme that was prebound to AMPPNP (Figs. 5 and 6). As above, the results obtained in the presence of Mg²⁺ and Ca²⁺ are analogous except that kinetic phases originating from DNA cleavage and religation are observed in the time traces with Ca²⁺ present, conditions that allow cleavage to take place, but not with Mg²⁺, which does not give substantial accumulation of cleaved DNA (8, 29, 31). The results in this section provide strong evidence that two enzyme species exist in the presence of AMPPNP, just as in its absence. We show that these species are characterized by markedly distinct DNA binding and release kinetics and that they can interconvert, indicating that they are not covalently different forms of the enzyme.

FIGURE 5.

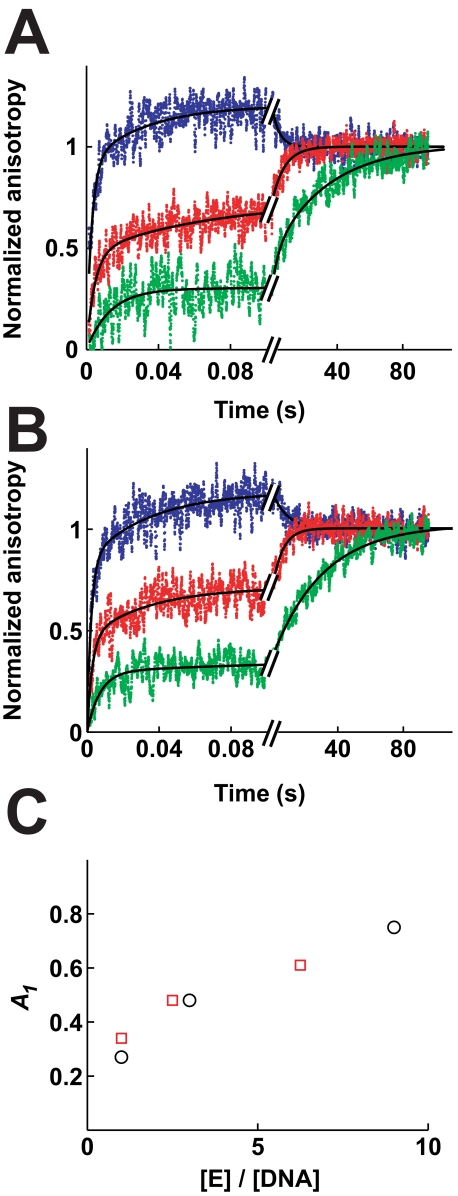
Binding of DNA to AMPPNP-bound enzyme. The association of enzyme and DNA was measured in Mg²⁺ (A) and Ca²⁺ (B) as in Fig. 2. Data from 9–23 separate injections were averaged for each experiment. A, 50 nm fluorophore-labeled DNA was rapidly mixed with 50 nm (green), 150 nm (red)/or 450 nm enzyme (blue, final concentrations). Lines, triple exponential fits with k₁ = 100 s^-1, k₂ = 5 s^-1, k₃ = 0.04 s^-1 (green); k₁ = 210 s^-1, k₂ = 14 s^-1, k₃ = 0.13 s^-1 (red); k₁ = 400 s^-1, k₂ = 15 s^-1, k₃ = 0.23 s^-1 (blue). B, 80 nm ROX-labeled DNA was rapidly mixed with 80 nm (green), 200 nm (red), or 500 nm enzyme (blue). Lines, triple exponential fits with k₁ = 200 s^-1, k₂ = 9 s^-1, k₃ = 0.03 s^-1 (green); k₁ = 320 s^-1, k₂ = 27 s^-1, k₃ = 0.15 s^-1 (red); k₁ = 370 s^-1, k₂ = 16 s^-1, k₃ = 0.15 s^-1 (blue). C, relative amplitude of the initial phase (A₁) increases with increasing enzyme to DNA ratios. Values for A₁ were taken from fits in A (circles) and B (squares).

FIGURE 6.

Dissociation of DNA from AMPPNP-bound enzyme. Dissociation in Mg²⁺ (A) and Ca²⁺ (B) is measured as in Fig. 3. Data from 7 to 11 separate injections were averaged for each experiment. A, enzyme and fluorophore-labeled DNA were allowed to react for 70 ms (green) or >1 min (red) before the reaction mixture was chased with excess unlabeled DNA. Enzyme concentrations before the chase were 400 nm (green) and 350 nm (red). Fluorophore-labeled DNA concentrations were 100 nm (green) and 240 nm (red). Solid lines, double exponential fits (Equation 2). Best fit values are as follows: k₁ = 19 s^-1, A₁ = 0.18, k₂ = 1.0 s^-1, A₂ = 0.82; (red) and k₁ = 31 s^-1, A₁ = 0.58; k₂ = 2.2 s^-1, A₂ = 0.42 (green). B, enzyme (350 nm) and ROX-labeled DNA (280 nm) were mixed and equilibrated before the mixture was chased as above. The data are fit to a double exponential expression (k₁ = 27 s^-1; A₁ = 0.15; k₂ = 0.023 s^-1; A₂ = 0.85). Dashed line, single exponential fits for comparison.

Two different reaction schemes for the Mg²⁺ and Ca²⁺ data were considered. Scheme 1 depicts all steps, including the chemical steps as they take place in Ca²⁺. The supplemental Scheme S2 is a simplified version of Scheme 1 that lacks the chemical steps but is otherwise identical. This latter scheme was used to interpret the binding and release data in the presence of Mg²⁺, as these conditions do not allow significant DNA cleavage.

Fig. 5 depicts DNA association kinetics with the AMPPNP-bound enzyme. When stoichiometric concentrations of enzyme and DNA are mixed together, only a fraction of the DNA associates in the initial binding phase. Most of the DNA binds orders of magnitude more slowly, with an observed rate constant of 0.04 s^-1 in Mg²⁺ (Fig. 5A) and 0.03 s^-1 in Ca²⁺ (Fig. 5B). When the enzyme concentration is increased while keeping the DNA concentration the same, the relative amplitude of the initial association phase increases (Fig. 5C). These results strongly suggest the existence of two enzyme species E and E′ that bind DNA with significantly different rate constants (k_on and k′_on; Schemes 1 and S2). The larger fraction of DNA that is bound rapidly by the enzyme at higher enzyme to DNA ratios in Fig. 5C is expected in this model as the amount of the enzyme species that can bind DNA fast is increased. Moreover, the model quantitatively accounts for the data (supplemental Fig. S3 and Table 1).

Competing models that do not require the coexistence of two enzyme species are ruled out, as described in the supplemental material. We considered mechanisms that postulate a homogeneous enzyme population but in which either the DNA is heterogeneous or the DNA can bind to two different binding sites (supplemental Scheme S6, A and B). Importantly, a model in which the two enzyme species are not able to interconvert also cannot account for the data (supplemental material). The two enzyme species are therefore conformationally and not covalently different.

A modest decrease of the anisotropy in the association kinetic traces characterized by a rate constant of 0.23 and 0.15 s^-1 in Mg²⁺ and Ca²⁺, respectively, occurs in the DNA association curves with enzyme concentrations exceeding six times the DNA concentration. This decrease is most likely also present at lower enzyme/DNA ratios but cannot be detected under those conditions because it is masked by a phase with a similar rate constant but stronger positive amplitude. Models that assign each enzyme-DNA complex the same fluorescence anisotropy cannot account for a decrease in the anisotropy. Most likely, the complex between fluorophore-labeled DNA and enzyme slowly isomerizes to a conformation with a reduced anisotropy. Whether this conformation is only populated with fluorophore-labeled DNA or is also accessible with unlabeled DNA is not known. Because of this uncertainty and because the conclusions herein are not dependent on the nature of this phase we do not consider it further.

Because enzyme free in solution can adopt two conformations, enzyme bound to DNA can in principle also assume two conformations. To seek kinetic evidence for two enzyme-DNA species, we measured dissociation of DNA from the AMPPNP-bound enzyme. Indeed, the DNA dissociation kinetic traces in the presence of Mg²⁺ and AMPPNP are biphasic indicating the presence of two enzyme-DNA complexes (Fig. 6A). Moreover, the fast dissociating enzyme-DNA complex can be kinetically enriched by shortening the time the enzyme is allowed to associate with DNA before the chase is added (Fig. 6A). DNA religation as the source of one of the two phases can be discounted because only very small amounts of cleaved DNA accumulate with Mg²⁺ and AMPPNP present (<3%; data not shown and see Ref. 29). Instead, the dissociation kinetic data strongly suggest the existence of two enzyme-DNA species that are able to interconvert. The data are in quantitative agreement with such a model (supplemental Fig. S3).

Whereas the DNA dissociation data are consistent with a model that postulates two enzyme-DNA species, other models can in principle also lead to biphasic dissociation kinetics. We considered three possible competing models; each can be ruled out, as described in the supplemental material, based on the observed DNA association and dissociation kinetics. The first model predicts that the DNA, not the enzyme, is heterogeneous (supplemental Scheme S6A). The second model postulates that the two DNA-binding sites on the same enzyme species exist with one site releasing DNA faster than the other (supplemental Scheme S6B). The third model assumes that two noninterconverting enzyme species exist, one releasing DNA more slowly than the other (supplemental Scheme S5B).

DNA also dissociates in multiple phases when Mg²⁺ is replaced by Ca²⁺ (Fig. 6B). The kinetic trace is dominated by a single phase with an amplitude of 85%. The rate constant of this phase (0.023 s^-1) is indistinguishable from the observed rate constant for DNA religation under equivalent conditions (0.018 s^-1; supplemental Fig. S4). This phase therefore likely represents DNA religation. Because the kinetic trace is dominated by a single phase and because the signal of the data is limited, we cannot accurately disentangle rate constants for the other phases. The DNA dissociation kinetic data in the presence of Ca²⁺ and AMPPNP therefore cannot provide direct evidence for a conformational isomerization that occurs after DNA binding, as they do in Mg²⁺. Nevertheless, DNA cleavage data collected with Ca²⁺ present indicate that such a conformational change also exists (see below).

The Two Enzyme Conformations, E and E′, Cleave DNA with Different Observed Rate Constants—The multiphasic DNA association kinetics presented above provided strong evidence for two enzyme conformations, E and E′. DNA binding to E is fast (k_on = 10⁹ m^-1 s^-1; Table 1). Conversely, DNA binding to the other enzyme conformation, E′, is severely hindered (k′_on < 10⁶ m^-1 s^-1). If the association between E′ and DNA and the interconversion between the E and E′ are slow relative to DNA cleavage, the observed cleavage kinetics of both enzyme species would differ. In this case cleavage by the fast binding enzyme (E) can be isolated when enough of it is in solution to quickly bind all available DNA molecules. Conversely, under conditions where only a fraction of the DNA molecules are bound fast because the fast binding enzyme species is outnumbered by DNA molecules, the cleavage by the slow binding enzyme species (E′) can be determined. To better characterize the two enzyme conformations and to identify conditions under which the cleavage kinetics is not limited by a slow interconversion or association reaction, we obtained DNA cleavage time courses with constant, saturating concentrations of enzyme and varying substoichiometric DNA concentrations in the presence of AMPPNP (supplemental Fig. S1).

With enzyme concentrations in large excess over the DNA concentration, conditions that allow all DNA to bind at the diffusion limited rate, DNA cleavage followed an observed rate constant of 0.23–0.25 s^-1 (supplemental Fig. S1). The rate constant decreased and leveled off at 0.035 s^-1 when the DNA concentration approached the enzyme concentration, conditions in which the cleavage kinetics of the slow binding enzyme species is probed.

The results confirm the presence of two enzyme conformations. We show in the supplemental material that the enzyme species are able to interconvert as predicted by a model in which cleavage by E′ is slowed by a slow association with DNA and conversion to E. To prevent the slow step in the cleavage reaction of E′ from masking details of the cleavage kinetics, we chose enzyme concentrations in large excess of the DNA concentrations for the analysis of the cleavage reaction catalyzed by nucleotide-free enzyme above and the AMPPNP-bound enzyme below.

AMPPNP Binding Is Coupled to Steps Associated with Cleavage of the First but Not the Second DNA Strand—We next extracted kinetic information about the cleavage reaction in AMPPNP. To this end we obtained DNA cleavage progress curves in the presence of AMPPNP with the DNA dumbbell duplex as the cleavage substrate (Fig. 7). This and the following section describe and interpret specific features of these DNA cleavage time courses.

FIGURE 7.

DNA cleavage time courses of dumbbell DNA in the presence of saturating concentrations of AMPPNP. 300 nm (diamonds and triangles) or 900 nm enzyme (squares and circles) was preincubated with AMPPNP and then mixed rapidly with 1 nm DNA dumbbell (final concentrations). The formation of single (circles and diamonds) and double strand breaks (squares and triangles) was measured as described in Fig. 4. The right panel depicts the formation of the single strand break within the first 300 ms and reveals that formation of the single strand break follows a kinetic lag. Varying the enzyme concentrations between 300 and 900 nm has no noticeable effect on the kinetic lag. Solid and broken lines represent a global fit of the time courses to Scheme 2A. A kinetic lag is not obtained in fits of the data to a simpler model lacking a conformational step prior to cleavage of the first DNA strand (dotted line; supplemental Scheme S3).

Most generally, AMPPNP binding accelerates the observed cleavage kinetics and, as noted previously (8, 26, 27, 29), leads to an increase of the equilibrium levels of DNA cleavage (compare Fig. 4D with Fig. 7; see also supplemental Fig. S6). The equilibrium levels of both single and double strand breaks are affected by AMPPNP binding; single strand breaks increase from ∼9 to 14% and double strand breaks from 44 to 67%. Remarkably, the ratio of single to double strand breaks in the absence and presence of AMPPNP is very similar (4.9 and 4.8, respectively). This ratio is directly related to the equilibrium describing cleavage of the second strand (K_clvg,2; Scheme 2A). The data therefore strongly suggest that AMPPNP binding does not affect K_clvg,2. Previously proposed models in which AMPPNP acts subsequent to DNA cleavage, e.g. by allowing the gap formed by the double strand break to widen (36, 37), are therefore not supported by our data.

A fit of the data to the mechanism shown in Scheme 2A provides estimates for the rate constants underlying the second cleavage equilibrium (Fig. 7, solid and dashed lines; Table 2). Those rate constants are also unaffected, within error, by AMP-PNP, providing strong additional support for a mechanism in which AMPPNP has no influence on steps subsequent to cleavage of the first strand. The effect of AMPPNP on the cleavage kinetics must therefore be mediated through one or more steps up to and including cleavage of the first DNA strand.

An Isomerization of the Enzyme-DNA Complex Precedes the First Chemical Step—The cleavage time courses in Fig. 7 unveiled additional features of the DNA cleavage reaction. The formation of the double strand break follows a lag in the presence of AMPPNP (inset), as in its absence (Fig. 4D). As explained above, this lag is expected because the second strand can only be cleaved after the first. However, formation of the single strand break also exhibited a time lag in the presence of AMPPNP (Fig. 7, right panel). This lag was unaffected when the enzyme to DNA ratio was increased from 300:1 to 900:1 (right panel).

Such a lag could have its origin in a step that precedes DNA binding (k_iso in Scheme 1), in a partially rate-limiting binding step (k_on), or in a step between DNA binding and cleavage of the first strand (k′_iso). Simple models that do not include any of these steps cannot account for the presence of the lag (dashed line, supplemental Scheme S3). We rule out the first two models in the supplemental material on the basis that these models predict the lag to vary when the enzyme concentration was varied. Conversely, the third model, in which there is an additional step after binding but before cleavage, can quantitatively account for the DNA cleavage time courses (Fig. 7, solid and dashed lines). Furthermore, the biphasic DNA dissociation kinetics in Mg²⁺ provided independent evidence for such a step (Fig. 6A). Thus, we included a step between DNA binding and the first chemical step in the minimal model to account for the DNA cleavage data.

A comparison of Tables 1 and 2 shows that the rate constants for this additional step (k′_iso and k′_-iso) determined by the DNA cleavage assay are different from the corresponding rate constants determined by the fluorescence anisotropy assay. In contrast to the anisotropy assay, the cleavage assay can monitor not only thermodynamically favorable but also unfavorable reaction steps (supplemental Results). As discussed in the supplemental Results, the difference in the rate constants probably stems from an additional, thermodynamically unfavorable reaction step that follows the favorable step detected by the anisotropy assay. The conformational change after DNA binding and cleavage accordingly would consist of (at least) two substeps, one being thermodynamically favorable and one unfavorable. Because the existence of a second conformational step is not certain and because these substeps do not affect the overall physical and mechanistic conclusions drawn herein, we do not subdivide K′_iso into these two proposed steps.

An Overall Kinetic and Thermodynamic Model for the DNA Cleavage Reaction and Its Regulation by Nucleotide Binding

In this section we propose a minimal mechanism that unifies the thermodynamic and kinetic data presented above. We demonstrate that the observed DNA strand cleavage cooperativity and the effect of AMPPNP on the DNA cleavage reaction require and thus confirm the existence of a conformational change of the enzyme-DNA complex prior to cleavage of the first DNA strand. Moreover, we show that no additional conformational steps need to be assumed to fully account for the data.

As shown above, cleavage of the second strand is fast after the first cut has been introduced (i.e. positive observed kinetic cooperativity). Additionally, the observed cleavage of the first strand is thermodynamically less favorable than cleavage of the second (K_{clvg,1, obs} < K_clvg,2; thermodynamic cooperativity). Cooperativity can be explained by two scenarios.

In the first scenario, the chemical environments for the two DNA strands bound to the enzyme are inherently different, such that one strand is cleaved with a different rate constant than the other. However, in this scenario the strand that can be cleaved at a faster rate is cleaved rapidly followed by slow cleavage of the second strand. The model thus predicts the opposite effect of what is observed, i.e. negative observed kinetic cooperativity.

If the chemical environments for the two strands are not different, then one or more nonchemical steps in the cleavage framework would have to mediate the cooperativity (scenario 2). The location of these steps can be narrowed. A putative conformational step between the two chemical steps could only decrease and therefore not explain the observed thermodynamic cooperativity (see supplemental Results for a mathematical derivation). Moreover, although a thermodynamically favorable step after cleavage of the second strand could explain the thermodynamic cooperativity, such a step fails to account for the kinetic cooperativity (supplemental Results). However, a step prior to cleavage of the first strand (K′_iso in Scheme 2A) can account for the observed kinetic and thermodynamic cooperativity.

In the simplest model the K′_iso step is not only necessary but also sufficient to explain the observed cooperativity. If it were sufficient, K′_iso would fully mediate the cooperativity, and the rate constants for the two chemical steps would be the same (k_clvg,1 = k_clvg,2 and k_-clvg,1 = k_-clvg,2). This model gives a good fit to the data both in the absence of AMPPNP (Fig. 4D, lines) and in its presence (Fig. 7, solid and dashed lines).

We tested whether the kinetics of the reverse reaction, religation of the two strands, is accurately predicted by this model. As the nucleotide-free enzyme (see above), the AMPPNP-bound enzyme religated the single and double strand break with observed rate constants that match within 50% the rate constants predicted by the model (k_{obs, single break} = 0.024 s^-1, k_{obs, double break} = 0.028 s^-1; k_{pred, single break} = k_{pred, double break} = 0.02 s^-1; supplemental Fig. S5B).

Although K′_iso is necessary and sufficient to explain the cooperativity effect, we cannot rule out that additional steps located elsewhere in the cleavage framework also contribute. However, evidence for such steps does not exist. We have interpreted the data with the simplest model that can fully account for all of the data.

The unifying model must also explain the modulation of DNA cleavage by AMPPNP and not just the observed cleavage cooperativity. As shown above, AMPPNP binding accelerates the observed kinetics for formation of single and double strand breaks and augments the cleavage levels. To account for the faster appearance of the single strand break in the presence of AMPPNP, AMPPNP must minimally affect the first chemical step (K_clvg,1) or a step preceding it. An effect of AMPPNP on binding of DNA is not observed (k_on; Table 1) and could in any case not account for the faster appearance of the single strand break as saturating concentrations of enzyme were employed. In principle, AMPPNP binding could directly couple to the chemical step (K_clvg,1) or mediate its effect via a conformational change prior to cleavage (K′_iso). The first model requires a direct contact between both active sites which so far has not been observed (Fig. 1). On the other hand, conformational changes upon AMPPNP binding are well documented. Moreover, our DNA dissociation data provided evidence for an AMPPNP-induced conformational change after DNA binding that can take place under conditions in which cleaved DNA does not accumulate (in Mg²⁺; Fig. 6A), suggesting that an AMPPNP-driven conformational change can take place in the absence of and thus prior to DNA cleavage. A conformational step prior to DNA cleavage (K′_iso) therefore most likely takes part in mediating the effects of AMPPNP on the cleavage reaction. The simplest hypothesis is that AMPPNP binding does not alter the reaction scheme subsequent to K′_iso and that no additional conformational steps contribute to the AMPPNP effect.

To test if the isomerization step (K′_iso) could entirely mediate the cooperativity and the AMPPNP effects we globally fit the cleavage time courses obtained with nucleotide-free and AMP-PNP-bound enzyme to this unifying mechanism. AMPPNP was only allowed to couple to k′_-iso in the global fit because k′_-iso was the only rate constant that was significantly modulated by AMPPNP binding in the individual fits (Table 2). The simple unifying mechanism has only five independent parameters (see legend of supplemental Fig. S6). The global fitting algorithm identified values for these five parameters that result in an excellent fit of all available DNA cleavage data, including the kinetic lags observed for formation of single and double cut DNA (supplemental Fig. S6). A free energy profile according to the best fit values for this unifying mechanism is depicted in Fig. 8.

We emphasize that this minimal reaction mechanism has a single rate constant for the first and second DNA cleavage steps in the presence or absence of nucleotide. The ability to globally fit the data with such a strong modeling constraint and the reasonability of a model with a common environment for cleavage at both subunits after an activating conformational change are appealing. Nevertheless, as is always the case, more complex models cannot be ruled out that might include additional effects of AMPPNP or additional steps. Although our data show that the enzyme-DNA complex must change conformations to efficiently cleave DNA, the enzyme species prior to this conformational change (E_SS, Scheme 2) may also allow limited DNA cleavage.

A Structural Model for the Regulation of DNA Cleavage by AMPPNP Binding That Corresponds to the Kinetic and Thermodynamic Framework Established Herein

The kinetic and thermodynamic data presented above strongly imply the existence of a conformational rearrangement of the enzyme prior to DNA binding and of the enzyme-DNA complex following DNA binding. In this section we propose a simple structural explanation for these conformational changes that unifies prior structural data with these new functional data.

The DNA association, dissociation, and cleavage data indicate that the conformational steps (K_iso and K′_iso) are sensitive to the presence of AMPPNP. Thus, conformational changes known to be induced by AMPPNP binding are strong candidates for the isomerization steps that we have identified.

Crystallographic analysis of topoisomerase fragments containing the ATPase region bound to a variety of nucleotides and nucleotide analogs identified two conformational changes that occur upon ATP binding (10, 15, 19, 20, 38). With nucleotides bound, the two ATP binding domains in the homodimeric enzyme can self-associate (“dimerize”), allowing the enzyme to form a clamp that can entrap DNA (Fig. 1, ATP binding domains are in red). The second conformational change promoted by nucleotides is a rotation (“docking”) of the ATP binding module relative to the domain that connects the ATP binding module to the DNA cleavage domain (15, 20, 21, 38) (see also supplemental Scheme S4). This domain is thought to transmit signals from the ATP hydrolysis reaction to the DNA cleavage region of the enzyme and hence was dubbed the “transducer domain” (yellow in Fig. 1). However, the three-dimensional structure of the transducer does not change upon docking, suggesting that the DNA cleavage domains do not sense this conformational change (15, 19–21, 38). For these reasons, docking by itself without concomitant dimerization is presumably not sensed by the DNA cleavage domains (see supplemental material for a detailed discussion). The closure of the ATPase domains induced by nucleotide binding thus stands out as the simplest and most likely conformational change that takes place during the isomerization steps we have identified. Additionally, both enzyme halves undergo a symmetrical rearrangement during closure of the ATPase domains, consistent with the rate constants for the first and second chemical steps being identical (k_clvg,1 = k_clvg,2 and k_-clvg,1 = k_-clvg,2, see above). Based on the above, we propose that E possesses an open and E′ a closed ATPase gate (Scheme 2B).

This assignment predicts that at equilibrium a fraction of the ATPase gates are closed even in the absence of nucleotides, consistent with earlier electron microscopy results (39). Moreover, it assumes that the ATPase domains can close when Ca²⁺ is the sole divalent ion present in the buffer, consistent with the previous observations that Ca²⁺ can support the full reaction cycle of yeast topoisomerase, albeit at a reduced rate (40), and that divalent ions are not required to crystallize the ATPase domains of DNA gyrase in a dimeric form (18). Furthermore, the enzyme possesses a DNA-stimulated ATPase activity in Ca²⁺ as well as in Mg²⁺.4 As there is considerable evidence that the ATPase domains must close before hydrolysis (12–14, 18), this observation supports that dimerization can take place in Ca²⁺. To further test our prediction, assays will have to be developed that are capable of measuring the fraction of open and closed ATPase gates at equilibrium under assay conditions.

DNA topoisomerase can cleave DNA even in the absence of the ATPase domains (41), suggesting, if the model presented does hold, that the cleavage domains themselves can undergo the conformational changes necessary for cleavage and that the conformational changes of the ATPase domains couple to and thus regulate these transitions.

Whether docking of the ATP binding module against the transducer within the already dimerized ATPase domains is sensed by the DNA cleavage domains remains an interesting possibility. Although nucleoside triphosphate binding promotes both docking and dimerization (10, 19, 20, 38), hydrolysis of the nucleotides or subsequent ADP or inorganic phosphate release might uncouple docking from dimerization. In addition, it has been suggested that mixed nucleotide states occur during the ATPase reaction (9, 24, 25). Mixed nucleotide states could allow the two protomers to assume different conformations, adding to the possibilities of controlling DNA cleavage and T-DNA transport by the ATPase domains. The development of biophysical and biochemical techniques to measure and manipulate the dimerization and docking equilibria of the ATPase domains will provide the means necessary to directly test our model and to further dissect the regulatory roles of the ATPase domains.

We have recently discovered a conformational rearrangement step of the enzyme-DNA complex that is involved in selecting the cognate cleavage site (34). This conformational change takes place prior to DNA cleavage and is thermodynamically unfavorable, the same properties of the isomerization step that we independently identified herein (Fig. 8). We therefore propose that both steps are part of the same global conformational rearrangement; the ATPase domains swing together allowing the DNA cleavage domains to examine, select, and cleave the DNA strands.

Model for the Strand Passage Reaction Catalyzed by DNA Topoisomerase II

Our results can be seamlessly integrated into current mechanistic models of the topoisomerase II-catalyzed DNA transport. As suggested above, DNA binds to the enzyme species with open ATPase domains (Fig. 1, step 1). Binding of two ATP molecules leads to dimerization of the ATP binding modules, closing the ATPase gate (10–13, 19). The ATPase domains can thereby capture a T-DNA segment (Fig. 1, step 2) (11). We proposed above that closure of the ATPase domains activates G-DNA cleavage (Fig. 1, step 3). Hydrolysis of the first ATP takes place, which in turn stimulates transport of T-DNA through the gate in the G-DNA (9). The mechanism of coupling between ATP hydrolysis and T-DNA transport is not known, but it possibly involves undocking of the transducer from the ATP binding module (Fig. 1, dotted line) in response to ATP hydrolysis or phosphate release (steps 4 and 5) (15). The ATPase clamp stays closed even after hydrolysis of one ATP (42, 43) but can reopen when the second ATP is hydrolyzed, and the hydrolysis products are released to allow another round of catalysis (Fig. 1, step 6) (14, 44).

CONCLUSIONS AND IMPLICATIONS

A profound understanding of the mechanism of a molecular machine such as DNA topoisomerase II requires knowledge of the individual reaction steps and the energy transduction mechanism. Herein we have extended knowledge about the identity, order, and rates of individual reaction steps carried out by topoisomerase II from the elegant inspection of the ATPase cycles (9, 24, 25, 45) to its DNA cleavage and ligation reactions. Future pre-steady state investigations can now be carried out to learn how these cycles are interdigitated in the topoisomerase catalytic cycle. As DNA topoisomerase II and its bacterial homologs are targets for various clinically important antibiotics and chemotherapeutics (36, 46–49), such in-depth mechanistic understanding of these machines may facilitate the development of future clinical applications.

A Unifying Mechanism for the Coupling between Nucleotide Binding and DNA Cleavage

We have analyzed the control of the DNA cleavage activity of DNA topoisomerases II by the ATPase reaction. To this end, we established a minimal framework for the DNA cleavage reaction by measuring rate and equilibrium constants for individual steps catalyzed by nucleotide-free enzyme, and we monitored the perturbation of the framework caused by binding of the ATP analog AMPPNP. Our working model may guide the design of future experiments for direct experimental validation of the proposed mechanism and for a more detailed dissection of the intra-molecular communication.

Our data reveal a conformational change of the enzyme that can take place prior to and immediately after binding DNA. Based on its nucleotide sensitivity and previous information about the effect of nucleotides on the structure of the enzyme, we propose that the ATPase gate closes during this conformational rearrangement (Scheme 2, A and B). As summarized below, the gate must close before DNA cleavage can take place efficiently and must reopen to release DNA.

The structural assignment of the two enzyme conformations can explain the greater than 1000-fold differences in the DNA association rate constants of the two conformations (Table 1). Because DNA must enter through the gates formed by the ATPase domains, a closed ATPase gate (E′ species; Scheme 1) presumably hinders DNA access, accounting for the remarkably slow DNA binding rate constant of this conformer (k′_on < 10⁶ m^-1 s^-1; Table 1).

The assignment of the two enzyme conformations to the open and closed gate conformation also provides a simple structural explanation for the control that the ATPase domains exert on the DNA cleavage reaction. Because the DNA binding to the closed gate conformation is severely hindered, DNA binds to an appreciably extent only to the species with an open ATPase gate. However, this enzyme species is not competent to cleave DNA in our model, and the enzyme must first close the ATPase gate before cleavage can take place (Scheme 2, A and B). The model thus implies that closure of the ATPase domains precedes DNA cleavage and that the ATPase cycle of the enzyme can communicate with the DNA cleavage reaction by way of closing and opening the ATPase domains. Once this gate is closed, the model predicts identical kinetics and thermodynamics for the two DNA cleavage steps. The proposed mechanism thus implicates the ATPase domains as regulators of DNA cleavage with gate closure providing an on/off switch for cleavage of both DNA strands.

One might expect that the information about closure of the ATPase gate would be propagated to the cleavage domains by a number of smaller conformational changes. Indeed, our data provide evidence that the rearrangement takes place in at least two substeps, one being thermodynamically favorable and one unfavorable (see above and supplemental Results). Our model represents these substeps in terms of an overall conformational change in the isomerization step of Scheme 2 and Fig. 8.

Energy Transduction in DNA Topoisomerase II

Previous data in conjunction with our results provide insights into the use of the energy from ATP binding and hydrolysis during the DNA transport reaction of topoisomerase II. The binding energy of ATP is employed to induce dimerization of ATPase domains (10–13, 19). This conformational change is important for the structural transition used to capture T-segment DNA, based on prior work (Fig. 1) (11), and chemically to permit DNA cleavage, based on work herein coupled with previous structural results. Energy from the hydrolysis of ATP is utilized to reopen the ATPase clamps, a conformational change that is necessary to release the G-DNA (see above), to rebind another G-DNA segment (see above), and presumably to provide access to the T-DNA-binding site (11). Moreover, as successive turnover of the two bound ATP molecules accelerates DNA transport, the capacity to hydrolyze ATP serves an additional important functional role (9, 25), the biochemical basis of which remains to be elucidated. Structural data have suggested that undocking of the ATP binding and the transducer domains within the ATPase region plays a role in facilitating DNA transport (15). The docking equilibrium thus appears to be part of the series of conformational changes that transduce energy.

The DNA Cleavage Framework as a Foundation for an In-depth Mechanistic Analysis of Type II Topoisomerases

The DNA cleavage framework that we have developed for DNA topoisomerase II provides a foundation for further unraveling energy transduction in this complex and essential molecular machine. By preparing enzyme in additional nucleotide states, such studies can address the pressing question how topoisomerase II communicates events that succeed binding of nucleotides to other domains of the enzyme. Moreover, the mode of action of drugs that target the DNA cleavage activity of topoisomerase II (36, 46, 48) can now be readily tested. Also, the cleavage site selection process can be explored with unprecedented detail when the cleavage reaction of DNA duplexes with varying sequences are compared (34). Finally, the DNA dumbbell cleavage assay should be easily adaptable to the mechanistic dissection of other DNA-cleaving enzymes.