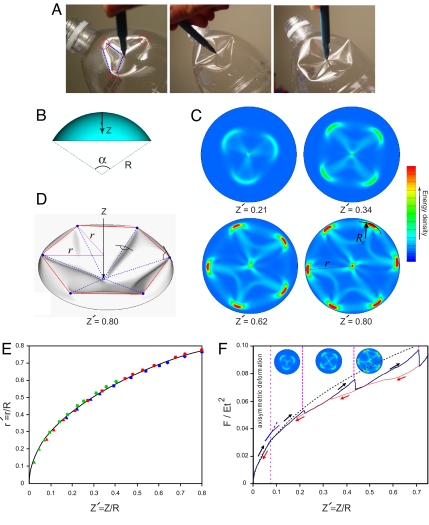
Fig. 1.

Indentation of a spherical cap. (A) Localization of deformation in a plastic bottle indented by a sharp pen. The deformation is localized approximately along a polyhedron with a triangular base (Left). As the indentation increases, one of the vertices bifurcates, leading to a polyhedral pattern with a square base (Center). Further indentation leads to further symmetry breaking (Right). (B) Schematic diagram of a clamped spherical cap with natural curvature R, indented at its center. (C) Elastic energy density in the elastic shell (t/R = 0.005) for various normalized indentations Z′ (see also Movie S1). The localization of deformation at the vertices is characterized by the localized region of radius R_c (see Fig. S1). (D) Typical deformed configuration of the elastic shell (t/R = 0.005 for a normalized indentation Z′ = Z/R = 0.8). The vertices lie approximately on a circle of r(Z). (E) The scaled radius r′ = r/R, versus the normalized center indentation, Z′. The solid line is given by 5, which for small indentations simplifies to $\mathrm{r\prime }\sim \sqrt{\mathrm{Z\prime }}$. The results from numerical simulations for different t/R (green: t/R = 0.001; red: t/R = 0.005; blue: t/R = 0.01), where filled triangles, squares, pentagons, and hexagons correspond to deformed configurations with 3, 4, 5, and 6 vertices, respectively. (F) Force–indentation response of an elastic shell with t/R = 0.005. Localization of deformation, which leads to formation of a pattern with three vertices, occurs at Z′ ∼ 0.076. The slopes of the response are shown at this indentation, which indicates ∼30% reduction in the apparent stiffness of the elastic shell as the asymmetric buckling pattern emerges, which is consistent with the analytical predictions (17, 18) as well as the approximate solution based on estimating the energy in the rim of the dimple. The dashed line is an approximate solution derived for axisymmetric deformations (14), and it compares qualitatively with the numerical simulations; however, as expected, it overestimates the forces relative to those for the faceted shell. All of the simulations were carried out for a cap with an opening angle α = 120°.