Analysis of Between-Trial and Within-Trial Neural Spiking Dynamics

Abstract

Recording single-neuron activity from a specific brain region across multiple trials in response to the same stimulus or execution of the same behavioral task is a common neurophysiology protocol. The raster plots of the spike trains often show strong between-trial and within-trial dynamics, yet the standard analysis of these data with the peristimulus time histogram (PSTH) and ANOVA do not consider between-trial dynamics. By itself, the PSTH does not provide a framework for statistical inference. We present a state-space generalized linear model (SS-GLM) to formulate a point process representation of between-trial and within-trial neural spiking dynamics. Our model has the PSTH as a special case. We provide a framework for model estimation, model selection, goodness-of-fit analysis, and inference. In an analysis of hippocampal neural activity recorded from a monkey performing a location-scene association task, we demonstrate how the SS-GLM may be used to answer frequently posed neurophysiological questions including, What is the nature of the between-trial and within-trial task-specific modulation of the neural spiking activity? How can we characterize learning-related neural dynamics? What are the timescales and characteristics of the neuron’s biophysical properties? Our results demonstrate that the SS-GLM is a more informative tool than the PSTH and ANOVA for analysis of multiple trial neural responses and that it provides a quantitative characterization of the between-trial and within-trial neural dynamics readily visible in raster plots, as well as the less apparent fast (1–10 ms), intermediate (11–20 ms), and longer (>20 ms) timescale features of the neuron’s biophysical properties.

INTRODUCTION

Understanding how neurons respond to putative stimuli is a fundamental question in neuroscience. Because neurons are stochastic, recording spiking activity from relevant brain regions during multiple presentations or trials of the same putative stimulus is a commonly used experimental paradigm for characterizing neural responses. Such neural recordings frequently have strong between-trial and within-trial dynamics (Fig. 1). The between-trial dynamics may represent random variations in the neuron’s response to the same stimulus or changes in how the neuron responds to the stimulus. The former may represent noise (Brody 1999; Dayan and Abbott 2001; Lim et al. 2006; Narayan et al. 2006; Ventura et al. 2005), whereas the latter may represent the evolution of a neuron’s receptive field properties (Brown et al. 2001; Gandolfo et al. 2000; Kaas et al. 1983; Mehta et al. 1997; Merzenich et al. 1984) or behavior-related changes such as learning and memory formation (Jog et al. 1999; Wirth et al. 2003; Wise and Murray 1999). The within-trial dynamics may reflect stimulus-specific or task-specific features of the neuron’s responses (Lim et al. 2006; Narayan et al. 2006; Wirth et al. 2003), short timescale biophysical properties, such as absolute and relative refractory periods and bursting, or longer timescale biophysical properties such as oscillatory modulations and other network and local regional characteristics (Dayan and Abbott 2001).

FIG. 1.

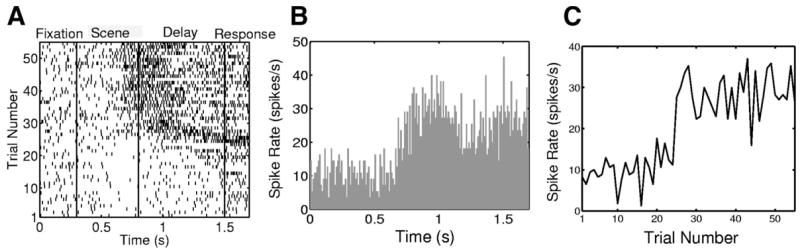
Fifty-five trials of spiking activity recorded from a hippocampal neuron of a macaque monkey in response to the same scene of a multiple location-scene association task presented as the raster plot (A), peristimulus time histogram (PSTH) (B), and trial-by-trial empirical spike rate function computed as the number of spikes across all trials divided by the trial length and by number of trials (C). Each trial is 1,700 ms in duration.

Two standard methods for analyzing neuron spiking dynamics are raster plots and the peristimulus time histogram (PSTH). Raster plots (Fig. 1A) are informative, two-dimensional graphs of spike times plotted as a function of trial number and time into the trial. However, they offer no means of quantitative analysis. The PSTH (Fig. 1B) is computed by totaling the spike counts within bins across trials and dividing by the trial length and number of trials (Abeles 1982; Gerstein 1960; Gerstein and Kiang 1960; Kass et al. 2003; Perkel et al. 1967). Although easy to compute, the PSTH assumes that the spiking activity between trials does not change, does not account for the effects of spike history on current spiking activity, and, by itself, does not provide a framework for statistical inference.

To go beyond use of raster plots, several authors have proposed analyses based on parametric or semiparametric statistical models to analyze between- and within-trial dynamics in neural activity (Brody 1999; Ventura et al. 2005). In these analyses, the components of the between- and within-trial dynamics are estimated sequentially rather than simultaneously, and the effects of history dependence within trial are not considered. Point process likelihood– based generalized linear models (GLMs) (Fahrmeir and Tutz 2001; McCullagh and Nelder 1989) have been used to analyze history dependence in neural spiking activity (Brillinger 1988; Brown et al. 2002, 2003; Kass and Ventura 2001; Paninski et al. 2004; Truccolo et al. 2005). GLM methods are available in nearly every statistical package and have the optimality properties and statistical inference framework common to all likelihood-based techniques. State-space modeling is a highly flexible signal processing paradigm (Durbin and Koopman 2001; Fahrmeir and Tutz 2001; Kitagawa and Gersch 1996; Mendel 1995) that has been applied in studies of neural dynamics including neural receptive field plasticity (Brown et al. 2001; Frank et al. 2002, 2004), neural coding analyses, neural spike train decoding (Barbieri et al. 2004; Brockwell et al. 2004; Brown et al. 1998; Deneve et al. 2007; Eden et al. 2004; Ergun et al. 2007; Paninski et al. 2004; Smith and Brown 2003; Wu et al. 2006), the design of control algorithms for brain–machine interfaces and neural prostheses (Shoham et al. 2005; Srinivasan et al. 2006, 2007a,b; Wu et al. 2006; Yu et al. 2007), and analyses of learning (Smith et al. 2004, 2005, 2007; Wirth et al. 2003). Although combined GLM and state-space methods have been developed in the statistics literature (Dey et al. 2000; Fahrmeir and Tutz 2001), these combined methods have not been used to analyze between-trial and within-trial dynamics of individual neurons.

We develop a state-space generalized linear model (SS-GLM) to formulate a point process representation of between-and within-trial neural spiking dynamics that has the PSTH as a special case. We estimate the model parameters by maximum likelihood using an approximate Expectation Maximization (EM) algorithm, assess model goodness-of-fit using Kolmogorov–Smirnov (K-S) tests based on the time-rescaling theorem, and guide the choice of model order with Akaike’s information criterion. We illustrate our approach using simulated hippocampal spiking activity and actual neural spiking activity of six hippocampal neurons recorded in a macaque monkey executing a learning experiment.

METHOD

We describe our SS-GLM framework and the experimental protocol from which the data analyzed in this study were collected.

A state-space generalized linear model of neural spiking activity

We assume that the spiking activity of a single neuron is a dynamic process that can be analyzed with the state-space framework used in engineering, statistics, and computer science (Durbin and Koopman 2001; Fahrmeir and Tutz 2001; Kitagawa and Gersch 1996; Mendel 1995). The state-space model consists of two equations: a state equation and an observation equation. The state equation defines an unobservable state process that will represent between-trial neural dynamics. Such state models with unobservable processes are often referred to as hidden Markov or latent process models (Durbin and Koopman 2001; Fahrmeir and Tutz 2001; Smith and Brown 2003). The observation equation defines how the observed spiking activity relates to the unobservable state process. The data we observe in the neurophysiological experiments are the series of spike trains. In our analyses the observation model will be a point process that depends on both between- and within-trial dynamics.

Point process observation model of neural spiking activity

We assume that the spike train that is the observation process of our state-space model can be represented as a point process (Brown 2005; Brown et al. 2003; Daley and Vere-Jones 2003; Kass et al. 2005). A point process is a time series of random binary (0, 1) events that occur in continuous time. For neural spike train, the 1’s are the individual spike times and the 0’s are the times of no spike occurrences. Given a trial interval (0, T], let N(t) be the number of spikes counted in interval (0, t] for t ∈ (0, T] in some trial. A point process model of a neural spike train can be completely characterized by its conditional intensity function, λ(t|H_t), defined as

$$\lambda (t\mid H_t)=\underset{\mathrm{\Delta }\to 0}{lim}\frac{Pr[N(t+\mathrm{\Delta })-N(t)=1\mid H_t]}{\mathrm{\Delta }}$$ (1)

where H_t denotes the history of spikes up to time t (Brown 2005; Brown et al. 2003; Daley and Vere-Jones 2003). It follows from Eq. 1 that given the history up to time t, the probability of a single spike in a small interval (t, t + Δ] is approximately λ (t|H_t)Δ. The conditional intensity function generalizes the definition of the rate function of a Poisson process to a rate function that is history dependent. Because the conditional intensity function characterizes a point process, defining a model for the conditional intensity function defines a model for the spike train.

To facilitate presentation of our model, we present the specific form of the conditional intensity function in discrete time. Assume that a repeated trial experiment is conducted with K trials of the same stimulus or task and neural activity is simultaneously recorded with the application of the stimulus or the execution of the task. We index the trials k = 1, …, K. We define the observation interval as (0, T], where T is the length of each trial. To obtain the discrete time representation of the conditional intensity function, we choose L large and divide the time interval T into subintervals of width Δ = TL⁻¹. We choose L large so that each subinterval contains at most one spike. We index the subintervals ℓ = 1, …, L and define n_k,ℓ to be the indicator, which is 1 if there is a spike in subinterval ((ℓ − 1)Δ, ℓΔ] on trial k and is 0 otherwise. We let n_k = {n_k,1, …, n_k,L} be the set of spikes recorded on trial k and N_1:k = {n₁, …, n_k} be the set of spikes recorded from trial 1 to trial k. We let H_k,ℓ denote the history of spikes in trial k, up to time ℓΔ.

We assume that the conditional intensity function for the spike trains recorded in our experiment at time ℓΔ of trial k has the form

$${\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })={\lambda }^S(\ell \mathrm{\Delta }\mid {\theta }_k){\lambda }^H(\ell \mathrm{\Delta }\mid \gamma ,H_{k,\ell })$$ (2)

where the component λ^S(ℓΔ|θ_k) describes the effect of the stimulus on the neural response and the component λ^H(ℓΔ|γ, H_k,ℓ) defines the effect of spike history on the neural response. The units of , λ_k(ℓΔ|θ_k, γ, H_k,ℓ) are spikes per second. By convention (Kass and Ventura 2001) we also take λ^S(ℓΔ|θ_k) in our analysis to have units of spikes per second and let λ^H(ℓΔ|γ, H_k,ℓ) be dimensionless. The idea to express the conditional intensity function as a product of a stimulus component and a temporal or spike-history component was first suggested by Kass and Ventura (2001). An important appeal of this approach is that if the spike-history component does not contribute to the model fit (i.e., if its value is close to 1 for all times), then Eq. 2 becomes an inhomogeneous Poisson process within each trial. In this way, Kass and Ventura pointed out that this formulation of the conditional intensity function makes it possible to measure the degree to which complex spiking models differed from more widely used Poisson models. Furthermore, the spiking model should explain two effects established as important in previous studies: the stimulus and spike-history effects (Dayan and Abbott 2001). Although there are many ways to model these two effects, Eq. 2 is equivalent to expressing the log of the conditional intensity function as the sum of these two effects (see Eq. 5). Therefore we can view this formulation as approximating the first two terms in a Wiener kernel expansion of the log of a general function of the stimulus and the spike history (Rieke et al. 1997). We have successfully used this formulation of the conditional intensity function in previous reports (Frank et al. 2002, 2004; Kass et al. 2005; Truccolo et al. 2005). If this formulation of the conditional intensity function fails to provide a good description of the data, then this lack of fit will be apparent in the goodness-of-fit analysis described in the following text. The parameters γ and θ_k are subsequently defined.

To model the effect of the stimulus or task on the neural spiking activity we assume that the first component of the conditional intensity function of Eq. 2 has the form

$$log{\lambda }^S(\ell \mathrm{\Delta }\mid {\theta }_k)=\sum _{r=1}^R{\theta }_{k,r}{g}_r(\ell \mathrm{\Delta })$$ (3)

where the g_r(ℓΔ) are a set of R functions that model the within-trial stimulus or task-specific effect on spiking activity parameterized by θ_k = {θ_k,1, …, θ_k,r, …, θ_k,R} for each trial k = 1, …, K. That is, Eq. 3 defines for each trial how the stimulus or task modulates the spiking activity. There is a different θ_k for each trial. We use a state-space model to define the relation between the θ_k values on different trials. This dependence defines the between-trial dynamics. There is flexibility in the choice of the g_r(ℓΔ) functions. Possible choices include polynomials, splines, and unit pulse functions. We use the unit pulse functions to represent the g_r(ℓΔ) values so that, as subsequently described, PSTH is a special case of our state-space model (Fig. 2).

FIG. 2.

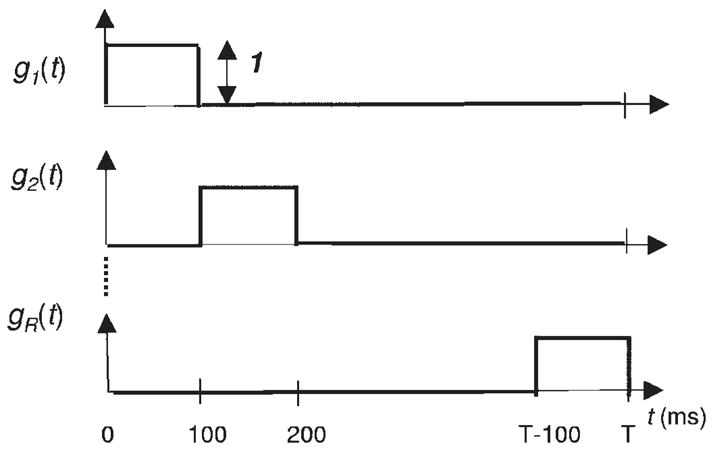
R orthogonal unit pulse basis functions (Eq. 9) defined on the interval (0, T].

To model the effect of spike history on current neural spiking activity, we assume that the second component on the right side of Eq. 2 can be defined as

$$log{\lambda }^H(\ell \mathrm{\Delta }\mid \gamma ,H_{k,\ell })=\sum _{j=1}^J{\gamma }_j{n}_{k,\ell -j}$$ (4)

for k = 1, …, K, where γ = (γ₁, …, γ_j, …, γ_J) is the vector of parameters that describes the dependence of the current spiking activity on recent spike history. In this model, we take the history to be H_k,ℓ = {n_{k,ℓ − J}, …, n_{k,ℓ − 1}}, which is the spiking activity during the preceding J time intervals prior to time ℓΔ. We chose the linear autoregressive expansion on the right side of Eq. 4 to relate the spike history to current spiking activity because it had been used successfully in many other spike train analyses (Brillinger 1988; Kass and Ventura 2001; Kass et al. 2005; Truccolo et al. 2005). The coefficients in the model in Eq. 4 capture spike-history effects at a resolution that is at most Δ. In the model in Eq. 4 we assume that the dependence on spike history defined by the parameter γ does not change across trials. However, the effects of the spike history will be different at different times because the history of spiking activity preceding different times differs.

By combining Eqs. 2, 3, and 4, we see that the conditional intensity function, which defines the observation equation of our state space model of neural activity, may be written as

$${\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })=exp\left\{\sum _{r=1}^R{\theta }_{k,r}{g}_r(\ell \mathrm{\Delta })\right\}exp\left\{\sum _{j=1}^J{\gamma }_j{n}_{k,\ell -j}\right\}$$ (5)

for k = 1, …, K and ℓ = 1, …, L. Equation 5 defines a GLM formulation of the conditional intensity function (Brillinger 1988; Kass and Ventura 2001; McCullagh and Nelder 1989; Truccolo et al. 2005). We perform the expansions in Eqs. 3 and 4 in terms of the logs of the stimulus and the spike-history components instead of in terms of the stimulus and spike-history components so that, as Eq. 5 shows, the analysis will always generate a conditional intensity or rate function that is positive.

State-space model of between-trial neural dynamics

To complete the definition of our state-space model and to model the relation of spiking activity between trials we define the state equation. We assume stochastic dependence between the θ_k = {θ_k,1, …, θ_k,r, …, θ_k,R} defined by the random walk model

$${\theta }_k={\theta }_{k-1}+{\epsilon }_k$$ (6)

for k = 1, …, K, where ε_k is an R-dimensional Gaussian random vector with mean 0 and unknown covariance matrix Σ. We also assume that the initial vector θ₀ is unknown. The random walk model provides a simple way to let the coefficients of the stimulus functions be different on different trials subject to a plausible constraint that prevents the model estimation problem from becoming intractable. It is reasonable to assume that the coefficients on the different trails are different to model between-trial dynamics. However, this assumption creates a challenging estimation problem if there is not a further constraint because it means that there is a large number of free parameters to estimate in each analysis. The constraint imposed by the random walk model is the plausible assumption that stimulus coefficients on trial k are close to the coefficients on trial k − 1. Equation 6 states this constraint in stochastic terms. That is, if no information is available, then given the coefficients on trial k − 1, the average or expected value for the coefficients on trial k is the value of the coefficient on trial k − 1. The variance about this mean is defined by Σ. Stated otherwise, given the coefficients on trial k − 1, and no other information, a good guess for values of the coefficients on trial k are the coefficients on trial k − 1. When spike train data are observed, the relation between θ_k and θ_k−1 is given by the Filter and Fixed-Interval algorithms in APPENDIX A. Equation 6 is a stochastic continuity constraint in that as the variance of ε_k values goes to zero, the probability that θ_k differs from θ_k−1 goes to zero. The smaller (larger) the components of Σ, the smaller (larger) the average difference between θ_k and θ_k−1 and the smoother (larger) the between-trial differences in the stimulus component.

Equations 5 and 6 define our state-space generalized linear model (SS-GLM). This model can be used to analyze between-trial and within-trial neural spiking dynamics provided we can estimate the unknown parameter ψ = (γ, θ₀, Σ). Because the values of θ_k are unobservable and ψ is an unknown parameter, we use the EM algorithm to compute their estimates by maximum likelihood (Dempster et al. 1977). The EM algorithm is a well-known procedure for performing maximum-likelihood estimation when there is an unobservable process or missing observations. In our model, the unobservable or hidden processes are the θ_k coefficients that define the between-trial dynamics. The EM algorithm has been used previously to estimate state-space models from point process observations with linear Gaussian state processes (Smith and Brown 2003). Our EM algorithm is based on the same ideas and its derivation is given in APPENDIX A. We denote the maximum-likelihood estimate of the model parameters ψ as ψ̂ = (γ̂, θ̂₀ Σ̂).

To understand what is accomplished in the EM model fitting, we note that the log of the joint probability density of the spike train data and the state process or the complete data log likelihood is (APPENDIX A, Eq. A1)

$$\begin{array}{l}logp(N,\theta \mid \psi )=\sum _{k=1}^K\sum _{\ell =1}^L[n_{k,\ell }log[{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\mathrm{\Delta }]\\ -{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })]\mathrm{\Delta }]+Klog({(2\pi )}^{-R/2}\mid \mathrm{\sum }{\mid }^{-1/2})\\ -2^{-1}\sum _{k=1}^K({\theta }_k-{\theta }_{k-1}{)}^{\prime }{\mathrm{\sum }}^{-1}({\theta }_k-{\theta }_{k-1})\end{array}$$ (7)

Equation 7 is a penalized log-likelihood function and shows, as mentioned earlier, that the random walk model (Eq. 6) for the stimulus coefficients imposes a multivariate stochastic smoothness or regularization constraint on the between-trial component of the conditional intensity or spike rate function (Fahrmeir and Tutz 2001; Kitagawa and Gersch 1996). The factor Σ⁻¹ is the smoothing or regularization matrix. In general, the larger the elements of Σ, the rougher the estimates of the between-trial component of the spike rate function, whereas the smaller the elements of Σ, the smoother the estimates of this component. Thus the maximum-likelihood estimate of Σ governs the smoothness of the spike rate function by determining the degree of smoothing that is most consistent with the data.

The PSTH and GLM are special cases of the SS-GLM

If we assume that the effect of the stimulus is the same between trials, then θ_k = {θ_k,1, …, θ_k,r, …, θ_k,R} = θ is the same for all trials. If we further assume that there is no dependence on spike history, then the GLM model becomes an inhomogeneous Poisson process with conditional intensity function

$${\lambda }_k(\ell \mathrm{\Delta }\mid \theta )=exp\left\{\sum _{r=1}^R{\theta }_r{g}_r(\ell \mathrm{\Delta })\right\}$$ (8)

for k = 1, …, K and ℓ = 1, …, L. Thus the conditional intensity function is the same for all trials k = 1, …, K. Next, we choose the basis functions g_r to be unit pulse functions with equal length

$$g_r(\ell \mathrm{\Delta })=\{\begin{array}{ll}1\hfill & \text{if }\ell =(r-1)L{R}^{-1}+1,\dots ,rL{R}^{-1}\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}$$ (9)

for ℓ = 1, …, L (Fig. 2). For the bin in which g_r(ℓΔ) = 1, the spiking activity obeys a homogeneous Poisson with mean rate exp(θ_r). It is easy to show that because the basis functions in Eq. 9 are orthogonal, the values exp(θ_r) (r = 1, …, R) can be estimated independently of each other. Furthermore, it can be shown that the maximum-likelihood estimate of exp(θ_r) is the number of spikes that occur in the bin in which g_r(ℓΔ) = 1, summed across all trials, divided by the number of trials and the bin width. This is equal to the height of the corresponding bar in a PSTH. Since this is true for all pulse functions, it follows that the PSTH is the maximum-likelihood estimate of the conditional intensity function defined by Eqs. 8 and 9. That is, we choose the unit pulse functions as the basis functions for the right side of Eq. 3 so that the PSTH is a special case of our SS-GLM model. Therefore we term the model Eq. 8, with the g_r values being equal-sized unit pulse functions (Eq. 9), the PSTH model.

The state-space model in Eqs. 5 and 6 is an extension of the GLM model in Truccolo et al. (2005). In that report, the stimulus effect is the same across trials. That is, the conditional intensity function has the form

$${\lambda }_k(\ell \mathrm{\Delta }\mid \gamma ,\theta ,H_{k,\ell })=exp\left\{\sum _{r=1}^R{\theta }_r{g}_r(\ell \mathrm{\Delta })\right\}exp\left\{\sum _{j=1}^J{\gamma }_j{n}_{k,\ell -j}\right\}$$ (10)

Thus the conditional intensity at trial k and time ℓΔ is a function of spike history in trial k and the time since the onset of the stimulus. This conditional intensity differs between trials because, in any given trial, it depends on the spike history in that trial. The spike history for different trials or, more generally, for different spike events is almost always different. This model can therefore capture implicitly between-trial neural dynamics. We refer to this model as a GLM model. Equations 2–4 make the GLM model with a log-link function (Eq. 10) a special case of our SS-GLM model when the coefficients of the stimulus term are the same for all trials. Truccolo et al. (2005) showed that this formulation of the GLM provided a simple way to perform maximum-likelihood analyses of neural spike trains by using a point process likelihood discretized at a resolution of Δ, readily available GLM fitting procedures such as glmfit in Matlab (The MathWorks, Natick, MA) and point process–based goodness-of-fit procedures based on the time-rescaling theorem as subsequently described.

Model goodness-of-fit

Before making an inference from a statistical model, it is crucial to assess the extent to which the model describes the data. Measuring quantitatively the agreement between a proposed model and a neural spike train or point process time series is a more challenging problem than measuring agreement between a model and continuous data. Standard distance measures applied in analyses of continuous data, such as average sum of squared errors, are not designed for point process data. One alternative solution to this problem is to apply the time-rescaling theorem (Brown et al. 2002; Ogata 1988; Truccolo et al. 2005) to transform point process measurements such as a neural spike train into a continuous measure appropriate for a goodness-of-fit assessment.

Once a conditional intensity function model has been fit to a neural spike train, we can compute rescaled times from the estimated conditional intensity function as

$$z_{k,m}=1-exp\left[{\int }_{u_{k,m-1}}^{u_{k,m}}{\lambda }_k(u\mid {\theta }_{k\mid K},\widehat{\gamma },H_{k,u})\text{d}u\right]$$ (11)

where u_k,m is the time of spike m in trial k for m = 1, …, M_k is the number of spikes in trial k for k = 1, …, K, and γ̂is the vector of maximum-likelihood estimates of the parameters γ. The vectors θ_k|K = (θ_k,1, …, θ_k,R) are the estimates of the unobserved states θ_k based on all K trials and ψ̂ on the maximum-likelihood estimates of the parameter ψ. We obtain θ_k|K from the E-step of the last EM iteration (APPENDIX A). The z_k,m values will be independent, uniformly distributed random variables on the interval [0, 1) if the conditional intensity function model is a good approximation to the true conditional intensity of the point process. Because the transformation in Eq. 11 is one to one, measuring the agreement between the z_k,m and a uniform distribution directly evaluates how well the original model agrees with the spike train data.

To evaluate whether the z_k,m values are uniformly distributed, we order the z_k,m from smallest to largest, denote the ordered values as z_k*, and plot the quantiles of the cumulative distribution function of the uniform density on [0, 1), defined as b_k* = (k* − 0.5)/K* against the z_k* for k* = 1, …, K*, where $K\ast ={\sum }_{k=1}^K(M_k-1)$ is the total number of interspike intervals to which the model was fit. We term these Kolmogorov–Smirnov (K-S) plots. If the model is consistent with the data, then the points should lie on a 45° line. Approximate large-sample 95% confidence intervals for the degree of agreement between a model and the data may be constructed using the distribution of the K-S statistic as b_k* ± 1.36K*^−1/2 (Brown et al. 2002).

Evaluating whether the z_k,m values are independent is in general difficult. Here we can take advantage of the structure of our problem and assess independence by further transforming the rescaled times to

$$z_{k,m}^G={\mathrm{\Phi }}^{-1}(z_{k,m})$$ (12)

where Φ(·) is the cumulative distribution function of a Gaussian random variable with zero mean and variance 1. If the rescaled times z_k,m are independent with a uniform distribution on the interval [0, 1), then the rescaled times $z_{k,m}^G$ are independent Gaussian random variables with mean 0 and variance 1 (and vice versa). Independence of a set of Gaussian random variables can be evaluated by analyzing the correlation structure because being uncorrelated is equivalent to being independent for Gaussian random variables. Thus if the $z_{k,m}^G$ are uncorrelated, then the $z_{k,m}^G$ are independent and thus the z_k,m are independent. We assess the independence of the rescaled times by plotting the autocorrelation function (ACF) of the $z_{k,m}^G$ (Eq. 12) with its associated approximate confidence intervals calculated as ±z_1−(α/2) K*^−1/2, where z_1−(α/2) is the 1 − (α/2) quantile of the Gaussian distribution with mean 0 and variance 1 (Box et al. 1994). If the ACF of the Gaussian rescaled times is indistinguishable from zero up to lag r, then we can conclude that the rescaled times are independent up to a lag r consecutive interspike intervals.

Model selection criteria

We fit several models to the neural spike train data and use Akaike’s Information Criterion (AIC) (Burnham and Anderson 1998; Truccolo et al. 2005) to identify the best approximating model from among a set of possible candidates. We evaluate the AIC as

$$\text{AIC}(p)=-2logP(N\mid \psi )+2p$$ (13)

where p is the dimension of ψ and log P(N|ψ) is the log likelihood of the observed data computed at the final iteration of the EM algorithm from Eqs. A2, A6, and A7 in APPENDIX A. Minimizing the AIC across a set of candidate models identifies a model from among the candidates that has approximately the smallest expected Kullback–Leibler distance to the “true” model (Burnham and Anderson 1998). Hence, in theory, the optimal model by this criterion is the one with the smallest AIC. In practice a small difference in AIC between two models may be due to random sample fluctuations. Therefore if the AIC difference between two models is <10, we choose the model with the smaller number of parameters. If the AIC difference between two models is >10, we conclude that the model with lower AIC explains substantially more structure in the data (Burnham and Anderson 1998).

The model we consider most appropriate to use to analyze the data is the one that: 1) is the best approximating model in terms of AIC and 2) gives the best summary of the data in terms of K-S and ACF plots.

Answering specific neurophysiological questions

Once the SS-GLM model has been estimated and its goodness-of-fit has been established, the principal objective is to use functions of the model and the model parameters to make inferences about the neural system being studied based on the recorded experimental data. An important property of maximum-likelihood estimation is invariance. That is, if ψ̂ is the maximum-likelihood estimate of a parameter ψ in a given model and h(ψ) is a function of ψ, then the maximum-likelihood estimate of h(ψ) is h(ψ̂) (Pawitan 2001). In particular, all of the optimality properties of maximum-likelihood estimation that are true for ψ̂ are also true for h(ψ̂) (Pawitan 2001). This seemingly obvious property is not true of all estimation procedures. We use this invariance principle explicitly in all of our analyses by simply computing h(ψ̂) as the obvious and optimal estimate of h(ψ).

The five principal, neurophysiologically relevant functions, h(ψ), we compute using this important property of maximum-likelihood estimation are: 1) the stimulus effect on the spiking activity; 2) the effect of spike history (intrinsic and network dynamics) on current spiking activity; 3) the spike rate per trial; 4) between-trial comparisons of the spike rate function; and 5) within-trial comparisons of the spike rate function. We show how these functions can be used to answer specific neurophysiological questions.

ESTIMATE OF THE STIMULUS EFFECT ON THE SPIKING ACTIVITY

From Eq. 3 it follows that the maximum-likelihood estimate of the stimulus effect, λ^S(ℓΔ|θ_k), at time ℓΔ and trial k, is

$${\lambda }^S(\ell \mathrm{\Delta }\mid {\theta }_{k\mid K})=exp\left\{\sum _{r=1}^R{\theta }_{k,r\mid K}{g}_r(\ell \mathrm{\Delta })\right\}$$ (14)

where θ_k|K = (θ_k,1, …, θ_k,R) is the estimate of the hidden state θ_k based on all K trials and on the maximum-likelihood estimates of the parameter ψ. We obtain θ_k|K from the E-step of the last EM iteration (APPENDIX A). The construction of simultaneous confidence intervals for the stimulus component is described in APPENDICES B and D.

ESTIMATE OF THE SPIKE-HISTORY FUNCTION

We denote exp{γ_j}, j = 1, …, J as the spike-history function, which describes the effects on spiking propensity of the absolute and relative refractory period as well as other biophysical properties such as rebound hyperpolarization and network dynamics. This function estimates the extent to which current spiking activity can be predicted from recent spiking history. Its maximum-likelihood estimate is

$$exp\{{\widehat{\gamma }}_j\}$$ (15)

for j = 1, …, J. Because each γ̂_j is the maximum-likelihood estimate of γ_j its approximate distribution is Gaussian (Pawitan 2001). Therefore we can use the fact that exp{γ̂_j} is approximately distributed as a lognormal random variable to compute the confidence intervals for exp{γ_j} (Smith and Brown 2003). The algorithm to compute the standard errors for the model’s spike-history component is given in APPENDIX C.

ESTIMATE OF THE SPIKE RATE FUNCTION

We define the expected number of spikes on trial k in the interval [t₁, t₂] as ${\mathrm{\Lambda }}_k(t_1,t_2)={\int }_{t_1}^{t_2}{\lambda }_k(u\mid {\theta }_k,\gamma ,H_{k,u})\text{d}u$. Furthermore, we define the spike rate function on interval [t₁, t₂] as

$${(t_2-t_1)}^{-1}{\mathrm{\Lambda }}_k(t_1,t_2)={(t_2-t_1)}^{-1}{\int }_{t_1}^{t_2}{\lambda }_k(u\mid {\theta }_k,\gamma ,H_{k,u})\text{d}u$$ (16)

The maximum-likelihood estimate of the spike rate function on trial k in the interval [t₁, t₂] is

$$\begin{array}{l}{(t_2-t_1)}^{-1}{\widehat{\mathrm{\Lambda }}}_k(t_1,t_2)={(t_2-t_1)}^{-1}{\int }_{t_1}^{t_2}{\lambda }_k(u\mid {\theta }_{k\mid K},\widehat{\gamma },H_{k\mid u})\text{d}u\\ \approx {(t_2-t_1)}^{-1}\sum _{l=l_1}^{t_2}{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_{k\mid K},\widehat{\gamma },H_{k\mid u})\mathrm{\Delta }\end{array}$$ (17)

where ℓ₁Δ = t₁ and ℓ ₂Δ = t₂. We compute confidence intervals for Λ_k(t₁, t₂) using the Monte Carlo method in APPENDIX E.

BETWEEN-TRIAL COMPARISONS OF THE SPIKE RATE FUNCTION

An important objective of these analyses is to compare spike rate functions between two trials. These comparisons are central to identifying a learning effect in behavioral learning experiments. We can do this by comparing the spike rates in the two trials in the same time interval. That is, for a given interval [t₁, t₂] and trials m and k we can compute using the maximum-likelihood estimates in Eq. 17

$$Pr[{(t_2-t_1)}^{-1}{\widehat{\mathrm{\Lambda }}}_m(t_1,t_2)>{(t_2-t_1)}^{-1}{\widehat{\mathrm{\Lambda }}}_k(t_1,t_2)]$$ (18)

for any k = 1, …, K − 1 and m > k. We compute this probability using the Monte Carlo methods described in APPENDIX F.

WITHIN-TRIAL COMPARISONS OF THE SPIKE RATE FUNCTION

A second important objective of these analyses is to compare the spike rate function between two disjoint periods within a trial. For example, it is important to compare spiking activity during a baseline period with spiking activity during another period in the trial such as the scene period or the delay period (Fig. 1). Differences in neural activity between a baseline and a specified period are used as one criterion to classify the neurophysiological properties of neurons (Wirth et al. 2003; Wise and Murray 1999). We compare the two spike rates on trial k given the two intervals [t₁, t₂] and [t₃, t₄] defined from Eq. 16 as

$${(t_4-t_3)}^{-1}{\mathrm{\Lambda }}_k(t_3,t_4)-{(t_2-t_1)}^{-1}{\mathrm{\Lambda }}_k(t_1,t_2)$$ (19)

and the maximum-likelihood estimate of the difference between these two spike rates is

$${(t_4-t_3)}^{-1}{\widehat{\mathrm{\Lambda }}}_k(t_3,t_4)-{(t_2-t_1)}^{-1}{\widehat{\mathrm{\Lambda }}}_k(t_1,t_2)$$ (20)

If the entire confidence interval for the difference between the two spike rate functions is positive (negative), then it is reasonable to infer that the spike rate function in period [t₃, t₄] is larger (smaller) than the spike rate in period [ t₁, t₂]. If the confidence interval for the difference in the two rates contains zero, then we conclude that the two spike rates do not differ. We compute confidence intervals for the difference (t₄ − t₃)^{− 1} Λ_k (t₃, t₄) − (t₂ − t₁)^{− 1} Λ_k(t₁, t₂) using the Monte Carlo methods in APPENDIX E.

Experimental protocol: location-scene association learning task

To illustrate our framework in the analysis of actual experimental data, we analyze responses of six hippocampal neurons recorded from macaque monkeys performing a location-scene association task. A detailed description of the experiment is in Wirth et al. (2003). The objective of that study was to characterize the response of the neurons to individual scenes and relate it to learning behavior. Here, we analyze in detail the responses of a single hippocampal neuron (see RESULTS) and we summarize the analyses of five other neurons.

The spikes of the neuron that we analyze in detail (RESULTS) were recorded during the presentation of the same scene across 55 trials. Each trial lasted 1,700 ms (Fig. 1A) and the spikes were recorded with a resolution of 1 ms. For this neuron, each trial time was divided into four epochs (Fig. 1A). These were: the fixation period from 0 to 300 ms; the scene presentation period from 300 to 800 ms; the delay period from 800 to 1,500 ms; and the response period from 1,500 to 1,700 ms. Across these 55 trials, this neuron fired 1,911 spikes in response to this scene.

RESULTS

Analysis of simulated multiple trial neural spiking activity

SIMULATING NEURAL SPIKING ACTIVITY

We first illustrate our SS-GLM framework in the analysis of simulated neural spike train data designed to reflect the structure of activity seen in learning experiments (Wirth et al. 2003). To simulate the data we constructed a point process model of the neural spiking activity whose conditional intensity function is a product of a stimulus and a spike history component (Eq. 2).

To construct the stimulus component of the model we chose cardinal splines as the basis functions g_r (Eq. 3), with R = 11 being the number of spline basis functions and with a control point vector being [t₁, …, t₁₁] = [0, 0, 0.25, 0.5, 0.75, 1, 1.25, 1.5, 1.75, 2, 2] (Frank et al. 2002; Hearn and Baker 1996). The stimulus component is then defined as (Fig. 3A)

FIG. 3.

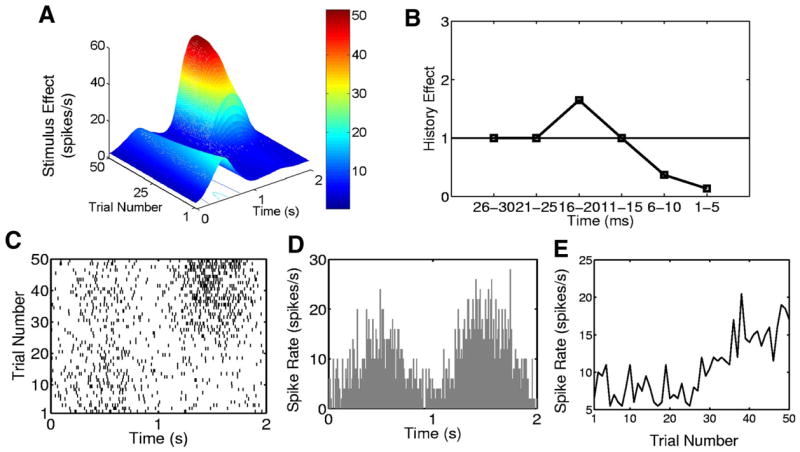
Simulated neural spiking activity from a 50-trial experiment. A: stimulus component of the conditional intensity function (Eqs. 21–23). B: history component (Eqs. 24 and 25) of the conditional intensity function. C: raster plot. D: PSTH. E: trial-by-trial empirical spike rate function. Each trial is 2,000 ms in duration.

$$\begin{array}{l}log{\lambda }^S(t\mid {\theta }_k)=[u{(t)}^{3}u{(t)}^{2}u(t)\text{ 1}]\\ \times \left[\begin{array}{cccc}-0.5& 1.5& -1.5& 0.5\\ 1& -2.5& 2& -0.5\\ -0.5& 0& 0.5& 0\\ 0& 1& 0& 0\end{array}\right]\times \left[\begin{array}{c}{\theta }_{k,r-1}\\ {\theta }_{k,r}\\ {\theta }_{k,r+1}\\ {\theta }_{k,r+2}\end{array}\right]\end{array}$$ (21)

for t ∈ (t_j, t_{j + 1}] and u(t) = (t − t_j)/(t_{j + 1} − t_j). The magnitudes of the spline functions at the control points, which are the stimulus parameters θ_k = [θ_k,1, …, θ_k,R] in our model, satisfy the deterministic state equation

$${\theta }_k=F_k{\theta }_{k-1}$$ (22)

where θ ₀ = [1, 1.7, 2.2, 3.1, 1.75, 1.75, 1.88, 1.88, 1.75, 1.75, 1] and where F_k is an 11-dimensional diagonal matrix whose diagonal elements evolve across the trials as

$$\begin{array}{l}\mathit{Trials}1to10:F_1=\mathit{diag}[\begin{array}{ccccccccccc}1& 1& 0.995& 0.995& 1& 1& 1& 1& 1& 1& 1\end{array}]\\ \mathit{Trials}11to15:F_2=\mathit{diag}[\begin{array}{ccccccccccc}1& 1& 0.995& 0.995& 1& 1.001& 1.001& 1.001& 1.001& 1& 1\end{array}]\\ \mathit{Trials}16to20:F_3=\mathit{diag}[\begin{array}{ccccccccccc}1& 1& 0.995& 0.995& 1& 1.001& 1.04& 1.04& 1.001& 1& 1\end{array}]\\ \mathit{Trials}21to30:F_4=\mathit{diag}[\begin{array}{ccccccccccc}1& 1& 0.995& 0.995& 1& 1.04& 1.04& 1.04& 1.04& 1& 1\end{array}]\\ \mathit{Trials}31to40:F_5=\mathit{diag}[\begin{array}{ccccccccccc}1& 1& 0.995& 0.995& 1& 1.01& 1.01& 1.01& 1.01& 1& 1\end{array}]\\ \mathit{Trials}41to47:F_6=\mathit{diag}[\begin{array}{ccccccccccc}1& 1& 0.995& 0.995& 1& 1.002& 1.002& 1.002& 1.002& 1& 1\end{array}]\\ \mathit{Trials}48to50:F_7=\mathit{diag}[\begin{array}{ccccccccccc}1& 1& 0.995& 0.995& 1& 1.001& 1.001& 1.001& 1.001& 1& 1\end{array}]\end{array}$$ (23)

The system in Eqs. 21–23 yields a stimulus component with two peaks that evolve between and within trials (Fig. 3A). The smaller peak between 0 and 1,000 ms decreases across the trials, whereas the larger peak, between 1,000 and 2,000 ms, rapidly increases after trial 25. For trials 1 to 25 the stimulus effect increases from 0 to 500 ms, decreases from 500 to 1,000 ms, and remains constant from 1,000 to 2,000 ms. From trials 26 to 50 the stimulus shows a lower magnitude increase and decrease between 0 to 1,000 ms and then shows a sharp increase and decrease from 1,000 to 2,000 ms.

We assume Δ = 1 ms and we define the history component of the model as (Fig. 3B)

$$log{\lambda }^H(\ell \mathrm{\Delta }\mid \gamma ,H_{k,\ell })=\sum _{j=1}^{20}{\gamma }_j{n}_{k,\ell -j}$$ (24)

where

$$\begin{array}{l}{\gamma }_1={\gamma }_2={\gamma }_3={\gamma }_4={\gamma }_5=-2\\ {\gamma }_6={\gamma }_7={\gamma }_8={\gamma }_9={\gamma }_{10}=-1\\ {\gamma }_{11}={\gamma }_{12}={\gamma }_{13}={\gamma }_{14}={\gamma }_{15}=0\\ {\gamma }_{16}={\gamma }_{17}={\gamma }_{18}={\gamma }_{19}={\gamma }_{20}=2\end{array}$$ (25)

We chose the first five parameters of spike-history component (Eq. 25) to be highly negative, to model the absolute and the early part of the relative refractory period of the simulated neuron (Fig. 3B). This is the value of exp(−2) in the 1- to 5-ms bins. Thus if the neuron fires once (twice) between 1 to 5 ms prior to time t, then the probability of a spike at time t decreases because it is multiplied by exp(−1 × 2) = 0.14 [exp(−2 × 2) = 0.02]. We chose the second five coefficients of the spike-history component for the 6- to 10-ms bins (Fig. 3B) to be −1 to model the later part of the neuron’s relative refractory period. If the neuron spiked once between 6 and 10 ms prior to time t, then the spiking probability is downweighted by multiplying the other components of the conditional intensity function by exp(−1) = 0.37. We chose the third set of five coefficients (11-to 15-ms bins) to be 0 so that a spike occurring in this time interval has no effect on the propensity of the neuron to spike at time t because exp(0) = 1. Finally, if the neuron spiked once between 16 and 20 ms prior to time t, then the probability of spiking at time t is increased by a factor of exp(γ ₄) = exp(0.5) = 1.65. Spiking activity ≥ 20 ms prior to the current time is assumed to have no effect on the spiking probability at the current time.

The conditional intensity function is therefore the product of the stimulus component defined in Eqs. 21–23 (Fig. 3A) and the history component defined in Eq. 24 and 25 (Fig. 3B). Following Kass and Ventura (2001), we constructed the stimulus component (Fig. 3A) with units of spikes per second and the spike-history component (Fig. 3B) as a dimensionless time-dependent scaling function. If the value of the spike history component is above (below, equals) one, then multiplying the stimulus component by the history component increases (decreases, does not affect) the firing rate.

We simulated neural spiking activity consisting of K = 50 trials each 2 s in length (Fig. 3C) by using the conditional intensity function defined in Eqs. 21–25 in a thinning algorithm (Brown et al. 2003, 2005). The simulated data (Fig. 3C), in which the PSTH is binned at 10 ms (Fig. 3D) and the spike rate is plotted as a function of trial (Fig. 3E), show patterns consistent with the between- and within-trial structure of the stimulus (Fig. 3A). The spike history component of the model cannot be discerned from these plots.

CANDIDATE MODELS, MODEL FITTING, AND MODEL SELECTION

To analyze the simulated data, we considered two models with a stimulus-only component: a PSTH (Eqs. 8 and 9) and a state-space PSTH [Eqs. 6, 8, and 9; λ^H(ℓΔ|γ, H_k,ℓ) = 1 for k = 1, …, K, ℓ = 1, …, L]. We also considered two types of models with a spike-history component: a GLM (Eqs. 9 and 10) and a state-space GLM (Eqs. 5, 6, and 9). We construct the spike-history components of the GLM models (Eq. 4) by considering spike dependence going back 300 ms prior to the current spike time using coarse time binning and fine time binning. The coarse time bins were 1–5, 6 –10, 11–15, 16 –20, 21–30, 31–50, 51–100, 101–150, 151–200, 201–250, and 251–300 ms. The fine time bins consisted of sixty 5-ms bins.

The model used to simulate the data differs from the SS-GLM model in two ways. First, we used a deterministic state equation (Eqs. 22 and 23) to ensure the presence of systematic change in the stimulus component and thus in the neural spiking activity both between and within trials. Such an evolution would occur by chance only with the random walk model in Eq. 6. Second, we used cardinal splines rather than unit pulse functions (Eq. 9, Fig. 2) to construct in the stimulus component (Fig. 3A) to guarantee smooth changes in the stimulus effect. By using a model to simulate the data that differs from the models used in the analysis we study the more realistic problem of analyzing data for which the “true model” is unknown.

We fit the GLM and PSTH models by maximum-likelihood estimation using GLMfit in Matlab. We fit the state-space models using the EM algorithms in APPENDIX A. To identify the best approximating model we used AIC and K-S goodness-of-fit tests based on the time-rescaling theorem and ACF of the transformed interspike intervals. An analysis of AIC as a function of the number of model parameters (Fig. 4) shows that in order of improving descriptive power (i.e., lowest AIC), the models are the PSTH, the SS-PSTH, the GLM with a 200-ms spike history with coarse binning, and SS-GLM with a 20-ms spike history and coarse binning (Table 1). Therefore to have a candidate from each type of model we consider, we choose these four models and analyze their fits in greater detail.

FIG. 4.

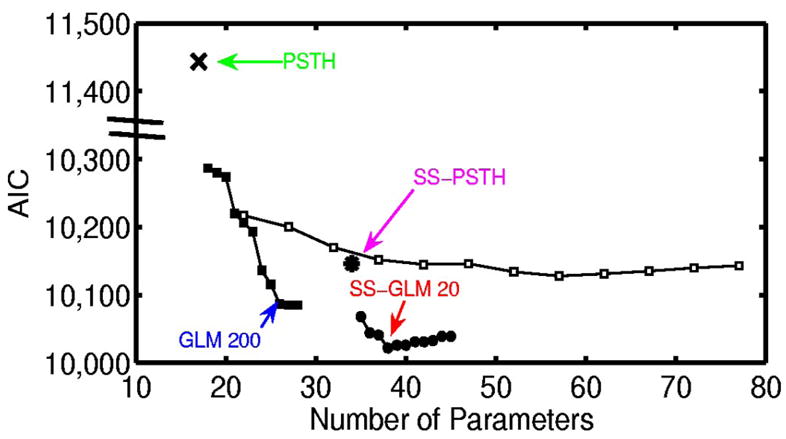
Akaike’s information criterion (AIC) (Eq. 13) for the analysis of the simulated neural spiking activity (Fig. 3) plotted as a function of the number of parameters for the candidate models: PSTH (×), generalized linear model (GLM) with coarse binning (black squares), state-space (SS)-PSTH (asterisk), GLM with fine binning (open squares), and SS-GLM with coarse binning (black circles). The model with the smallest AIC value provides the best approximating model in terms of minimum expected Kullbach–Leibler distance between the candidate model and the true model. The number of parameters is p, the dimension of ψ = (γ, θ₀, Σ) in Eq. 13. We construct the spike-history components of the GLM models (Eq. 4) by considering spike dependence going back 300 ms using coarse time binning and fine time binning. The coarse time bins were 1–5, 6 –10, 11–15, 16 –20, 21–30, 31–50, 51–100, 101–150, 151–200, 201–250, and 251–300 ms. The fine time bins consisted of sixty 5-ms bins. The best approximating model among the nonstate-space GLM models used coarse history dependence ≤ 200 ms defined as bins: 1–5, 6 –10, 11–15, 16 –20, 21–50, 51–100, 101–150, and 151–200 ms (GLM 200, blue). The best approximating model among all the models considered was the SS-GLM model with a 20-ms coarse history dependence defined as bins: 1–5, 6 –10, 11–15, and 16 –20 (SS-GLM 20, red). The model fits of the PSTH (green), GLM 200 (blue), SS-PSTH (pink), and SS-GLM 20 (red) are summarized in Table 1.

TABLE 1.

Summary of the four candidate models used in the analysis of simulated neural spiking activity (Fig. 3)

Model	Stimulus Component	Spike-History Component Bins, ms	Model Equation Formulas	Number of Parameters	AIC (Eq. 13)
PSTH	Same for all trials	None	Eqs. 8 and 9	17	11,444
GLM 200	Same for all trials	1–5, 6–10, 11–15, 16–20, 21–30, 31–50, 51–100, 101–150, 151–200	Eqs. 9 and 10	26	10,087
SS-PSTH	Changing across trials	None	Eqs. 6, 8, and 9	34	10,146
SS-GLM 20	Changing across trials	1–5, 6–10, 11–15, 16–20	Eqs. 5, 6, and 9	38	10,022

The SS-GLM 20 model gives the best data description in terms of minimum AIC.

The histogram of the rescaled interspike intervals (Fig. 5, A–D) and the K-S plots (Fig. 5I) assess the extent to which the distribution of the rescaled interspike intervals are uniform whereas the ACF (Fig. 5, E–H) assesses the extent to which the transformed times are approximately independent. If the rescaled times are uniformly distributed, the histograms in Figs. 5, A–D will be uniform and the K-S plot will be close to the 45 ° line. If the transformed times are independent, the ACF will be close to zero and within the 95% confidence intervals.

FIG. 5.

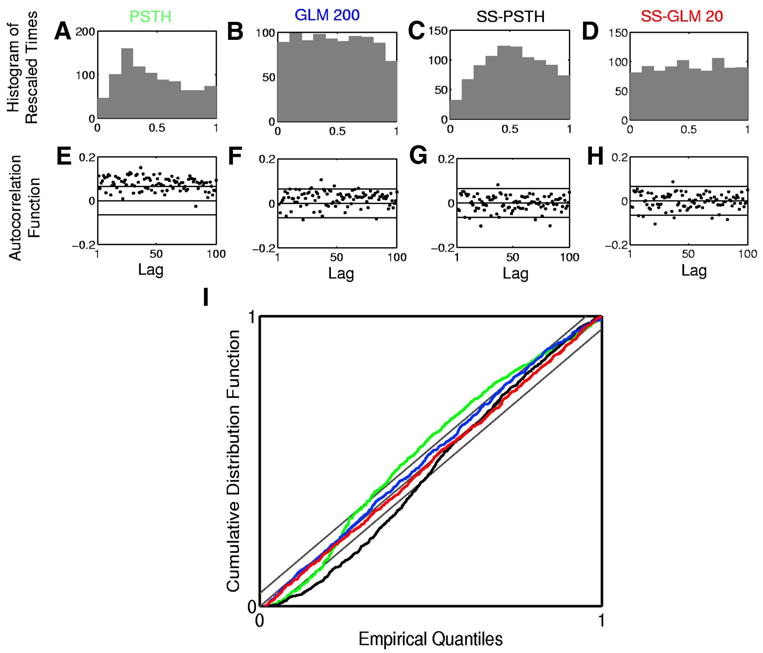
Goodness-of-fit analysis of the four models in Table 1 fit to the simulated neural spiking activity (Fig. 3). Row 1 shows the histogram of rescaled interspike intervals z_k,m (Eq. 11) derived from the (A) PSTH, (B) GLM 200, (C) SS-PSTH, and (D) SS-GLM 20 fits. Row 2 shows 100 lags of the autocorrelation function (ACF) for the Gaussian transformation of the rescaled interspike intervals $z_{k,m}^G$ (Eq. 12) derived from the (E) PSTH, (F) GLM 200, (G) SS-PSTH, and (H) SS-GLM 20 fits. I: Kolmogorov–Smirnov (K-S) plots for the PSTH (green curve), GLM 100 (blue curve), SS-PSTH (black curve), and SS-GLM 20 (red curve). The gray 45 ° line defines an exact model fit and the parallel gray lines define 95% confidence bounds.

Of the four models we consider, the PSTH describes the data least well in terms of the K-S and ACF analyses. The SS-PSTH model gives a good fit in terms of ACF but fits less well in terms of the K-S plot. The GLM 200 and the SS-GLM 20 agree closely with the data in terms of both the ACF and K-S plots. That is, for both the GLM 200 and the SS-GLM 20 the rescaled times are consistent with a uniform probability density and the ACF suggests that the transformed times are independent up to lags of 100 consecutive interspike intervals. The AIC, K-S, and ACF analyses suggest that the SS-GLM 20 provides the most parsimonious and accurate summary of the data. Therefore it is the preferred model to use to answer specific neurophysiological questions. The SS-GLM 20 model (Table 1) offers strong evidence that the within-trial dynamics described by the spike history of 20 ms and the between-trial dynamics described by the state-space are important components of the spiking activity.

TASK-MODULATION OF THE NEURAL SPIKING ACTIVITY

We next demonstrate how the SS-GLM 20 model can be used to answer specific neurophysiology questions. Because we know the true underlying structure in the data in this simulated example, we also compare the conclusions we draw from SS-GLM 20 with those we draw from the other three candidate models. First, we examine how the stimulus or the task modulates the spiking activity (Eq. 3). The SS-GLM 20 model gives an estimate of the stimulus component (Fig. 6D) as a function of trial and time within the trial. It demonstrates that the task-specific activity changes both between and within trials. The SS-GLM 20 (Fig. 6D) captures the three-dimensional structure in the true stimulus surface (Fig. 3A). This estimate is not smooth because the estimated stimulus component was constructed with the unit pulse functions (Fig. 2) instead of with the spline functions used to simulate the data. The fit of the SS-PSTH (Fig. 6C) is not as good as the SS-GLM 20. In addition, the SS-PSTH estimate of the three-dimensional structure in the stimulus (i.e., spike rate as a function of the stimulus as its between- and within-trial components) does not closely agree with the true stimulus component (Fig. 3A). By definition, the PSTH (Fig. 6A) and GLM 200 (Fig. 6B) models cannot provide estimates of the between-trial stimulus components.

FIG. 6.

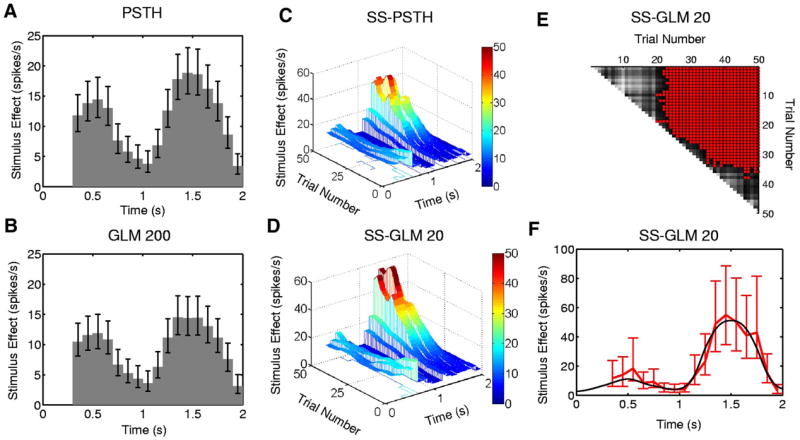
Stimulus component estimated from the simulated neural spiking activity (Fig. 3) for the (A) PSTH, (B) GLM 200 and approximate local 95% confidence intervals computed using the quantiles of the lognormal distribution. The estimated stimulus component from (C) the SS-PSTH and (D) the SS-GLM 20 model showing both the between- and within-trial dynamics. The entry in row k and column m of the matrix (E) gives a between trial comparisons of the spike rate functions from the SS-GLM 20 computed as the probability that the spike rate on trial m (x-axis) is greater than the spike rate on trial k (y-axis) (Eq. 18). Gray scale displays the comparisons (E) with light (dark) shades corresponding to low (high) probability. For contrast, red areas denote the trial comparisons for which the probability is greater than 0.95. F: the true stimulus component at trial 50 (black curve) and the estimated stimulus component of the SS-GLM 20 model (red curve) and 95% confidence intervals (bars).

To obtain another view of the between trial comparisons in spiking rates, we follow Smith et al. (2005) and compute the following probability matrix (Eq. 18) using the SS-GLM 20 model: The entry in row k and column m is the probability that the spike rate on trial m (x-axis in Fig. 6E) is greater than the spike rate on trial k (y-axis in Fig. 6E). The gray scale displays the comparison (Fig. 6E) with the light (dark) shades corresponding to a low (high) probability. For contrast, the red areas (Fig. 6E) show the trial pairs for which this probability is ≤ 0.95. This is not a significance test, but rather use of the approximate joint distribution of the maximum-likelihood estimates of the coefficients of the stimulus effect (APPENDICES B and F) to compute empirical Bayes’ estimates of these probabilities (Smith et al. 2005). As a consequence, there is no multiple hypothesis testing problem with these comparisons.

The first 23 rows show that from approximately trial 24 to trial 50, there is at least a 0.95 probability that spiking activity on these trials is greater than the spiking activity at trials 1 to 23. Rows between 23 and 35 show that spiking activity is steadily increasing between trials, although this rate is getting smaller. Finally at about trial 35 this increase in spiking activity between trials stops. The spiking activity between trial 36 and trial 50 does not differ because all the corresponding probabilities are >0.05 and <0.95, which is illustrated by the gray areas. Furthermore, the spiking activity between trial 1 and trial 20 does not differ. These differences are also suggested by the raster plot (Fig. 3A).

To provide an example of a more detailed analysis of the within-trial dynamics, we show for the true stimulus component at trial 50 (Fig. 6F, black curve), 95% simultaneous confidence intervals (Fig. 6F, red vertical lines with bars). The state-space model analysis gives an estimate of the joint distribution of the stimulus components of the model. Thus we can construct confidence intervals for any function of the stimulus that is of interest (METHODS, APPENDICES D, E, and F). The confidence intervals cover the true stimulus component for this trial. The PSTH (Fig. 6A) and the GLM 200 (Fig. 6B) provide an average rather than a trial-specific estimate of the stimulus effect. As a consequence, their confidence intervals fail to cover the true stimulus component at trial 50. We conclude that this neuron has a stimulus-specific response that has both strong between- and within-trial components. Thus Fig. 6E and F provide quantitative analyses of the structure seen in the raster plot (Fig. 3A) and confirm that there is a very high probability of both between- and within-trail task-modulated changes in this neuron’s spiking activity.

BETWEEN-TRIAL DYNAMICS AND LEARNING-RELATED EFFECTS

Characterizing between-trial dynamics in neural activity is important in behavioral experiments because a frequent objective of these studies is to relate the between-trial changes in neural activity to between-trial changes in behavioral variables such as a learning curve or reaction time measurements (Eichenbaum et al. 1986; Siegel and Castellan 1988; Smith et al. 2004, 2005, 2007; Wirth et al. 2003). The strong between-trial dynamics of this neuron were already evident in the estimated stimulus surface (Fig. 6D). To examine another representation of these between-trial dynamics that is closer to the between-trial spike rate estimate computed in learning experiments, we estimate the spike rate within 0.3 and 2 s (Eq. 17) for our four models: the PSTH, the SS-PSTH, the GLM 200, and the SS-GLM 20 (Fig. 7). The PSTH estimate of the between-trial spike rate dynamics (Fig. 7A) and its 95% confidence intervals are flat and do not capture the between-trial changes in rate. The GLM 200 model overestimates the between-trial changes in rate between trial 1 and trial 28 and underestimates it from trial 31 to trial 50 (Fig. 7B). The SS-PSTH and SS-GLM 20 models capture well the dynamics of the between-trial spiking dynamics because their 95% confidence intervals (APPENDIX E) cover the true change in spike rate between trials (Fig. 7, C and D).

FIG. 7.

Estimated spike rate (Eq. 17) by trial (black curve) and the 95% confidence intervals (black dashed curves) for the simulated neural spiking activity (Fig. 3) for the (A) PSTH, (B) GLM 200, (C) SS-PSTH, (D) SS-GLM 20 fits. The true spike rate per trial is given by the gray curve.

ANALYSIS OF INTRINSIC AND NETWORK DYNAMICS

We examine the spike-history component in detail by plotting the estimate obtained from the GLM 200 model (Fig. 8, A and B) and the SS-GLM 20 model (Fig. 8C). The estimate (Fig. 8C, solid line) is in good agreement with the true spike history effect because the 95% confidence intervals for this model cover the true history component (Fig. 8C, white squares). In contrast, the 95% confidence intervals for the spike-history function computed from the GLM 200 model do not cover the true spike-history function (Fig. 8A). The GLM 200 model overestimates the true history component at all time bins. The PSTH and the SS-PSTH models do not provide an estimate of the spike-history dependence.

FIG. 8.

Spike-history component (Eq. 15) for the simulated neural spiking activity (Fig. 3) estimated from the GLM 200 (A) and the SS-GLM 20 (C) models along with 95% confidence intervals (bars) and the true values of spike-history component (open squares). B: the first 5 coefficients (20 ms) of the spike-history component of the GLM 200 model plotted for better comparison with the SS-GLM 20 coefficients. The spike-history component of the SS-GLM 200 model was estimated with time bins of 1–5, 6 –10, 11–15, 16 –20, 21–50, 51–100, 101–150, and 151–200 ms. The spike-history component of the SS-GLM 20 model was estimated with time bins of 1–5, 6 –10, 11–15 and 16 –20 ms.

From this analysis we conclude that the spiking activity of this neuron is strongly modulated by a spike-history component for which the short-term components 1 to 10 ms most likely represent the intrinsic dynamics of the neuron such as the absolute and relative refractory period, whereas the components from 15 to 20 ms could represent late intrinsic dynamics and perhaps the effects of network dynamics (Truccolo et al. 2005).

In conclusion, the state-space GLM analysis provides a highly informative summary of the between- and within-trial dynamics of this neuron, which can be interpreted as possible learning-related dynamics (stimulus- or task-specific modulation), and intrinsic and network dynamics (spike-history component).

Analysis of actual multiple trial neural spiking activity

To illustrate our state-space GLM framework to characterize actual multiple trial neural spiking activity, we analyze the spike trains of the hippocampal neuron (Fig. 1) recorded from the monkey executing the location-scene association task (see METHODS). We demonstrate how to select the most appropriate model from among a set of candidate models to describe the data and show how that model may be used to characterize the properties of the neuron’s spiking activity and to answer specific neurophysiological questions.

CANDIDATE MODELS, MODEL FITTING, AND MODEL SELECTION

We considered two models with a stimulus-only component: a PSTH (Eqs. 8 and 9) and a state-space PSTH [Eqs. 6, 8, and 9; λ^H(ℓΔ|γ, H_k,ℓ) = 1 for k = 1, …, K, ℓ = 1, …, L]. We also considered two types of models with a spike-history component: a GLM (Eqs. 9 and 10) and a state-space GLM (Eqs. 5, 6, and 9). We construct the spike-history components of the GLM models (Eq. 4) by considering spike dependence going back 200 ms using coarse time binning and fine time binning. The coarse time bins were 1–2, 3–5, 6 –10, 11–20, 21–30, 31–50, 51–100, 101–150, and 151–200 ms. For the fine time binning the first two bins are 1–2 and 3–5 ms, whereas from 5 to 200 ms, we divide time into 39 bins, each 5 ms in width.

We fit the GLM and PSTH models by maximum likelihood using GLMfit in Matlab and the state-space models using the EM algorithms in APPENDIX A. Model selection and goodness-of-fit were carried out using AIC and K-S goodness-of-fit tests based on the time-rescaling theorem and ACF of the Gaussian transformed interspike intervals. An analysis of AIC as a function of the number of model parameters (Fig. 9) shows that in order of improving descriptive power (i.e., lowest AIC), the models are the PSTH, the SS-PSTH, the GLM with a 100-ms spiking history, and the SS-GLM with a 100-ms spiking history (Table 2). Therefore to have a candidate from each type of model we consider, we choose these four models and analyze their goodness-of-fit in greater detail.

FIG. 9.

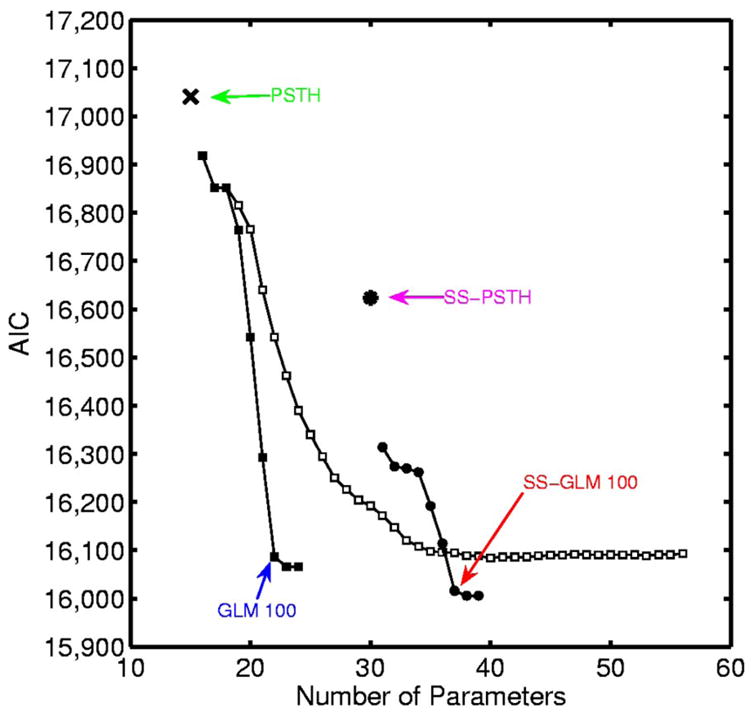
AIC for the analysis of the hippocampal neural spiking activity (Fig. 1) plotted as a function of the number of parameters for the candidate models: PSTH (×), GLM with coarse binning (black squares), SS-PSTH (asterisk), GLM with fine binning (open squares), and SS-GLM with coarse binning (black circles). The model with the smallest AIC value provides the best approximating model. The number of parameters is p, the dimension of ψ = (γ, θ₀, Σ) in Eq. 13. We construct the spike-history components of the GLM models (Eq. 4) by considering spike dependence going back 200 ms using coarse time binning and fine time binning. The coarse time bins are 1–2, 3–5, 6 –10, 11–20, 21–30, 31–50, 51–100, 101–150, and 151–200 ms. For the fine time binning the first 2 bins are 1–2 and 3–5 ms, whereas from 5 to 200 ms, we divide time into 39 bins each 5 ms in width. The best approximating model among the nonstate-space GLM models used coarse history dependence ≤ 100 ms defined as bins: 1–2, 3–5, 6 –10, 11–20, 21–30, 31–50, and 51–100 ms (GLM 100, blue). The best approximating model among all the models considered was the SS-GLM model also with a 100-ms coarse history dependence (SS-GLM 100, red). The model fits of the PSTH (green), GLM 100 (blue), SS-PSTH (pink), and SS-GLM 100 (red) are summarized in Table 2.

TABLE 2.

Summary of the four candidate models used in the analysis of hippocampal neural spiking activity

Model	Stimulus Component	Spike-History Component Bins, ms	Model Equation Formulas	Number of Parameters	AIC (Eq. 13)
PSTH	Same for all trials	None	Eqs. 8 and 9	15	17,041
GLM 100	Same for all trials	1–2, 3–5, 6–10, 11–20, 21–30, 31–50, 51–100	Eqs. 9 and 10	22	16,086
SS-PSTH	Changing across trials	None	Eqs. 6, 8, and 9	30	16,624
SS-GLM 100	Changing across trials	1–2, 3–5, 6–10, 11–20, 21–30, 31–50, 51–100	Eqs. 5, 6, and 9	37	16,016

The SS-GLM 100 model gives the best data description among the GLM (SS-GLM) models in terms of AIC.

Of the four models we consider, the PSTH describes the data least well in terms of the plots of the transformed times, ACF and K-S analyses (Fig. 10, A, E, and I, green curve). The SS-PSTH model gives a good fit in terms of ACF (Fig. 10G) but fits less well in terms of the transformed times and K-S plot (Fig. 10, C and I, black curve). The transformed times of the GLM 100 appear to be slightly more uniform (Fig. 10B) than those of the SS-GLM 100 (Fig. 10D). All of the ACF components of the SS-GLM 100 (Fig. 10H) appear to be independent up to a lag of 100 consecutive interspike intervals, whereas several of the ACF components of the GLM 100 (Fig. 10F) are outside the 95% confidence bounds, suggesting that these latter transformed times are not independent. The K-S plots of the GLM 100 (Fig. 10I, blue curve) and the SS-GLM 100 (Fig. 10I, red curve) are almost indistinguishable, as suggested by their respective plots of the transformed times (Fig. 10, B and D).

FIG. 10.

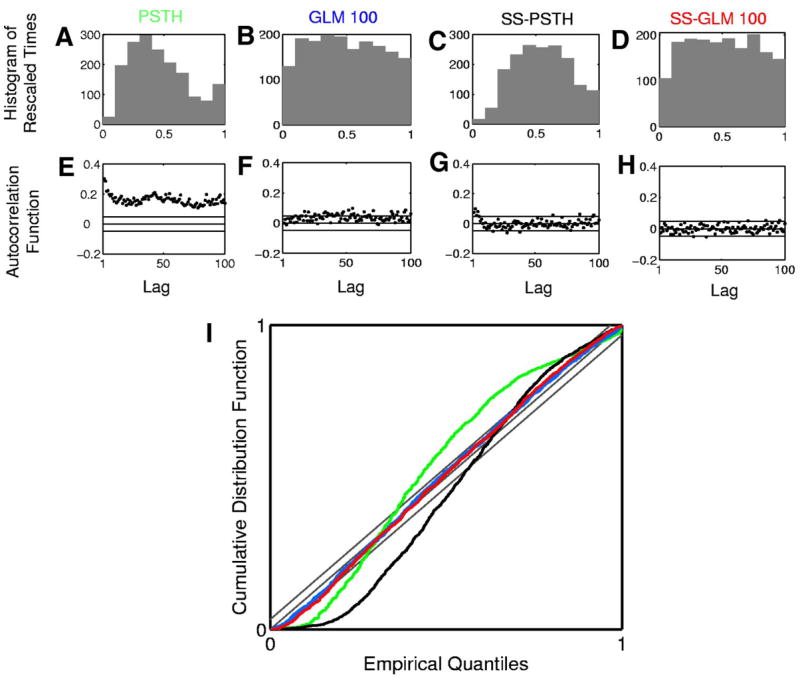
Goodness-of-fit analysis for the four models in Table 2 fit to the hippocampal neural spiking activity. Row 1 shows the histogram of rescaled interspike intervals z_k,m (Eq. 11) derived from the (A) PSTH, (B) GLM 100, (C) SS-PSTH, and (D) SS-GLM 100 fits. Row 2 shows 100 lags of the ACF for the Gaussian transformation of the rescaled interspike intervals $z_{k,m}^G$ (Eq. 12) derived from the (E) PSTH, (F) GLM 100, (G) SS-PSTH, and (H) SS-GLM 100 fits. I: K-S plots for the PSTH (green curve), GLM 100 (blue curve), SS-PSTH (black curve), and SS-GLM 100 (red curve). The gray 45 ° line defines an exact model fit and the parallel gray lines define 95% confidence bounds.

The AIC, K-S, and ACF analyses suggest that the SS-GLM 100 provides the most parsimonious and accurate summary of the data of the four models. Therefore it is the preferred model to use to answer specific neurophysiological questions. The SS-GLM 100 model (Table 2) offers strong evidence that the within-trial dynamics described by the spike history of 100 ms and the between-trial dynamics described by the state-space model are important components of the spiking activity. We next demonstrate how the SS-GLM 100 model can be used to answer specific neurophysiological questions and we compare the conclusions drawn from it with those drawn from the other three candidate models.

IS THERE TASK-SPECIFIC MODULATION OF THE NEURAL SPIKING ACTIVITY?

We first examine how the stimulus, which in this case is a location-scene association task, modulates the spiking activity (Eq. 3). The SS-GLM 100 model gives an estimate of the stimulus component (Fig. 11D) as a function of trial and time within the trial. As suggested by the raster plot of the spiking activity (Fig. 1A), the three-dimensional surface (Fig. 11D) shows that there are strong task-specific changes both between and within trials. This estimate is not smooth because the estimated stimulus component was constructed with the unit pulse functions (Eq. 9). The fit of the SS-PSTH is not as good as that of the SS-GLM 100. Furthermore, the SS-PSTH estimate of the stimulus (Fig. 11C) is about 1.4-fold higher than the stimulus component estimated from the SS-GLM 100 model (Fig. 11D). By definition, the PSTH (Fig. 11A) and GLM 100 (Fig. 11B) models cannot provide estimates of the between-trial stimulus components. The SS-GLM 100 model demonstrates that the location-scene association task strongly modulates the spiking activity of this neuron.

FIG. 11.

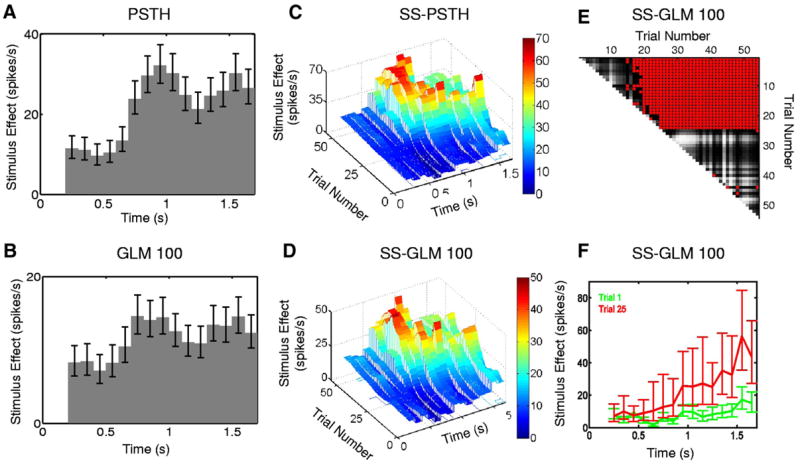
Stimulus component estimated from the hippocampal neural spiking activity (Fig. 1) using the (A) PSTH, (B) GLM 100, and approximate local 95% confidence intervals computed using the quantiles of the lognormal distribution. The estimated stimulus component from the (C) SS-PSTH and (D) SS-GLM 100 models showing both the between- and within-trial dynamics. The entry in row k and column m of the matrix (E) gives a between trial comparisons of the spike rate functions from the SS-GLM 100 computed as the probability that the spike rate on trial m (x-axis) is greater than the spike rate on trial k (y-axis) (Eq. 18). Gray scale displays the comparisons (E) with light (dark) shades corresponding to low (high) probability. For contrast, red (blue) areas denote the trial comparisons for which the probability is >0.95 (<0.05). F: the estimated stimulus component and 95% confidence intervals for trial 1 (green curve) and the estimated stimulus component and the 95% confidence intervals for trial 25 (red curve) from SS-GLM 100 model.

However, to make this statement firmly, it is important to conduct a formal statistical analysis of these changes. Our SS-GLM analysis estimates the joint probability distribution of the model’s stimulus components. Therefore we can construct confidence intervals or make probability statements about any given aspect of the stimulus using the Monte Carlo algorithms in APPENDICES D, E, and F. Using the SS-GLM 100 model, we compute, as we did for the simulated data example (Fig. 6E), the empirical Bayes’ probability matrix (Eq. 18) (Smith et al. 2005) in which the entry in row k and column m is the probability that the spike rate on trial m (x-axis in Fig. 11E) is greater than the spike rate on trial k (y-axis in Fig. 11E). The gray scale displays the comparison (Fig. 11E) with the light (dark) shades corresponding to a low (high) probability. For contrast, the red areas (Fig. 11E) show the trials for which this probability is ≥0.95.

The first five rows show that from trial 17 to trial 55 there is at least a 0.95 probability that spiking activity on these latter trials is greater than the spiking activity on trials 1 to 5 (Fig. 11E, red areas). Row 6 shows that from trial 19 to trial 55 there is at least a 0.95 probability that spiking activity on these trials is greater than the spiking activity on trial 6, whereas rows 7 to 19 show that from trial 20 to trial 55, there is a >0.95 probability that spiking activity on these trials is greater than the spiking activity on trials 19 or less. Finally, row 24 shows that spiking activity from trial 25 to trial 55 is greater than spiking activity on trials 1 to 24. In contrast, the spiking activity between trial 1 and trial 14 and between 25 and 55 do not differ because the corresponding probabilities are almost all (except of 6) >0.05 and <0.95 (Fig. 11E, dark gray areas).

Therefore we conclude that there is a very high probability of a difference in spike rate between trials beginning as early as trial 17 compared with the first six trials and definitively by trial 25 and all subsequent trials compared with all trials prior to trial 25. This latter difference is clearly evident in Fig. 1A. Thus Fig. 11, D and E provides quantitative analyses of the structure seen in the raster plot (Fig. 1A) and confirms that there is a very high probability that this neuron has strong between-trial, task-related modulation of its spiking activity.

The three-dimensional structure of the response surface (Fig. 11D) shows that our analysis provides for each trial a within-trial estimate of the task modulation of the neural spiking activity. To illustrate, we show the estimated stimulus component and its simultaneous 95% confidence intervals at trials 1 (Fig. 11F, green curve) and 25 (Fig. 11F, red curve). Because the 95% confidence intervals for the two curves do not overlap between 1.1 to 1.7 s, we conclude that the task-specific activity at trial 25 is greater than that at trial 1 within this time interval. Figure 11F shows that we can compute for any trial the within-trial estimate of the task-modulated dynamics and that we can compare these dynamics to those in any other trial. These trial-specific within-trial estimates of the task-modulated dynamics are more informative than the PSTH (Fig. 1B), which provides only an average estimate of the within-trial, task-modulated dynamics.

HOW CAN WE CHARACTERIZE BEHAVIOR-RELATED (BETWEEN-TRIAL) NEURAL DYNAMICS?

Characterizing between-trial dynamics in neural activity is important in behavioral experiments because a frequent objective of these studies is to relate the between trial changes in neural activity to between trial changes in behavioral variables such as learning curves or reaction time measurements (Eichenbaum et al. 1986; Siegel and Castellan 1988; Smith et al. 2004, 2005, 2007; Wirth et al. 2003). In this case, these between-trial dynamics may represent behavior-related changes.

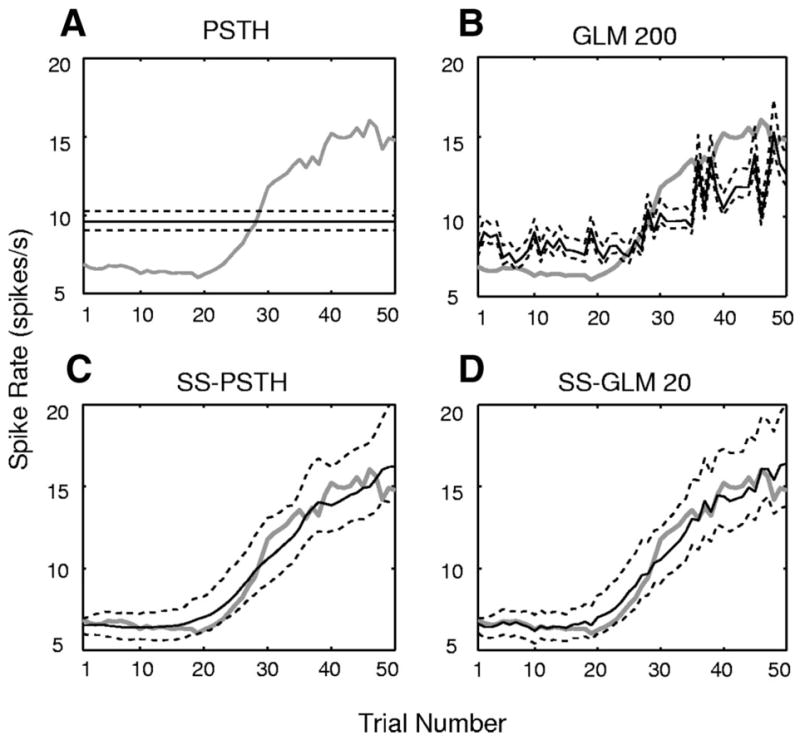
The strong between-trial dynamics of this neuron were already evident in the raster plot (Fig. 1A), the empirical spike rate function (Fig. 1C), the estimated response surface (Fig. 11D), the probability matrix (Fig. 11E), and the within-trial estimates of the task-specific activity (Fig. 11F). To provide another display of these between-trial dynamics that is closer to the empirical spike rate estimate (Fig. 1C), computed typically in multiple trial experiments as the number of spikes per trial divided by the trial length, we estimate the spike rate per trial within 0.2 and 1.7 s (Eq. 17), respectively, for the GLM 100 model (Fig. 12A) and the SS-GLM 100 model (Fig. 12B). The spike rate estimated from the GLM 100 model (Fig. 12B, solid black curve) exceeds the empirical spike rate (Fig. 12A, solid gray curve) between trial 1 and trial 24, whereas it underestimates the spike rate between trial 26 and trial 55. Moreover, because the GLM 100 model does not consider explicitly between-trial dynamics, its 95% confidence intervals (Fig. 12A, dashed black curve) estimate only a small amount of uncertainty in its spike rate. The SS-GLM 100 model estimate (Fig. 12B, solid black curves) and its wider 95% confidence intervals (Fig. 12A, dashed black curve) capture well the between-trial spiking dynamics. The empirical spike rate estimate (Fig. 12B, gray curves) is closer to the SS-GLM 100 estimate. Because we established in the goodness-of-fit analyses that the SS-GLM 100 model provides the best description of the data, its spike rate estimate is more credible and informative than either the GLM 100 or the empirical spike rate estimates (Figs. 1C and 12, gray curves). Therefore the SS-GLM model can be used to characterize the between-trial changes in this neuron’s spiking activity.

FIG. 12.

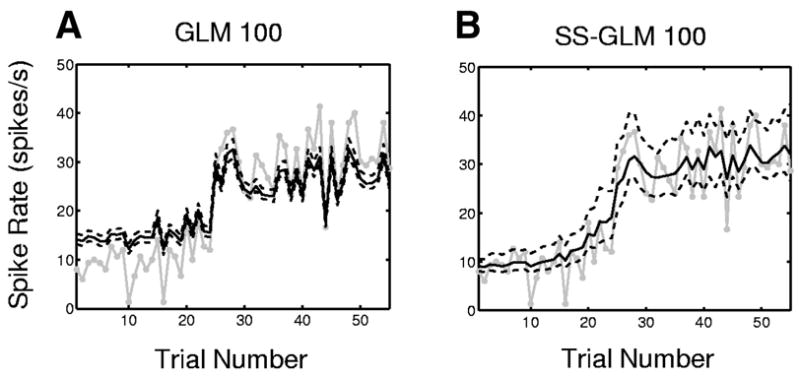
Spike rate by trial (black curve) and the 95% confidence intervals (black dashed curves) for the hippocampal neural spiking activity (Fig. 1) estimated from the (A) GLM 100 model, (B) SS-GLM 100 model (Eq. 17). The empirical spike rate estimate computed as the number of spikes per trial divided by the trial length is given by the gray curve.

IS THERE A DIFFERENCE IN TASK-SPECIFIC ACTIVITY BETWEEN THE BASELINE AND THE DELAY PERIODS?

An important question to answer at the start of the analysis of a neurophysiological experiment consisting of multiple trials is whether activity in a specified period of the task is different from activity in the baseline period. This analysis is performed at the start to determine whether a neuron has any evidence of task-specific activity. If the null hypothesis of no task-specific activity is rejected (not rejected) the neuron is included in (excluded from) further analysis. A standard convention is to use an ANOVA to answer this question (Wirth et al. 2003; Wise and Murray 1999). This approach is usually less than optimal because, except in the case of extremely high spike rates, neural spiking activity is rarely well described by the Gaussian assumptions that are required to correctly apply ANOVA. Although we have already shown with the analyses in Figs. 11 and 12 that this neuron has strong task-specific modulation of it is spiking activity, we demonstrate that the appropriate analog of this ANOVA can be carried out very easily using our SS-GLM framework.

The question we ask is, “Is there a difference in task-specific activity between the delay period (Fig. 1, 800 –1,500 ms) and the fixation period (Fig. 1, 0 –300 ms)?” We consider the fixation period as a baseline period and the delay period as a period of possible task-specific activity. We used one-way ANOVA on the spike rates estimated from the PSTH and found significant task-specific activity with P < 0.05. The ANOVA does not give details about the differences in response across the task without a further post hoc testing analysis. Using the SS-GLM 100 we estimated the difference in the spike rates for each trial using Eq. 20 with t₁ = 200, t₂ = 300, t₃ = 800, t₄ = 1,500 ms. The estimate of this difference by trial (black curve) with 95% confidence intervals (black dashed curves) is shown in Fig. 13. The estimate of this difference is positive from trial 15 to trial 55 and the lower bound of the 95% interval for the difference is positive from trial 20 to trial 55. Therefore our analysis confirms the ANOVA finding of task-specific activity and shows that the difference between the activity in the delay and fixation periods is significant beginning at trial 20. The empirical estimate of the observed rate difference (Fig. 13, gray curve) computed on each trial as the number of spikes in the delay period divided by the length of the delay period minus the number of spikes in the baseline period divided by the length of the baseline period suggests a similar conclusion, but is noisier and does not provide confidence intervals.

FIG. 13.

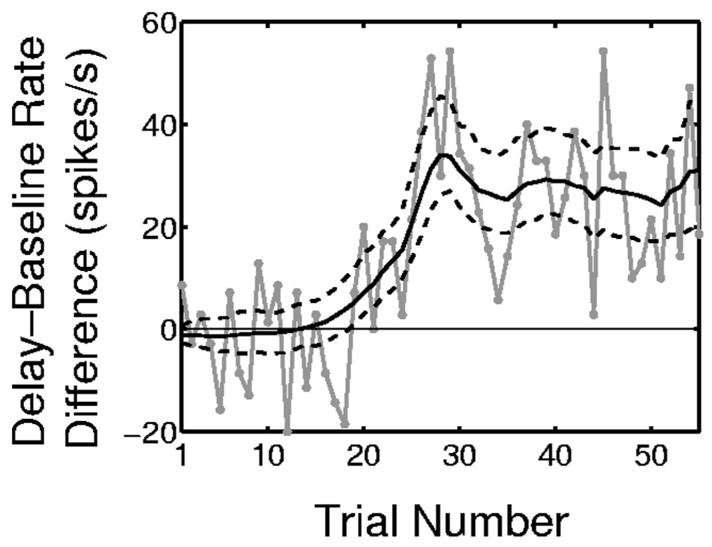
Within-trial comparisons of the difference in the spike rates of the delay periods (800 to 1,500 ms) and the baseline period (0 to 300 ms) derived from the SS-GLM 100 analysis of the hippocampal spiking activity (Fig. 1). The solid black curve is the estimated spike rate difference (Eq. 20), the dashed black curves are the 95% confidence intervals, and the gray curve is the empirical estimate of the observed rate difference computed on each trial as the number of spikes in the delay period divided by the length of the delay period minus the number of spikes in the baseline period divided by the length of the baseline period.

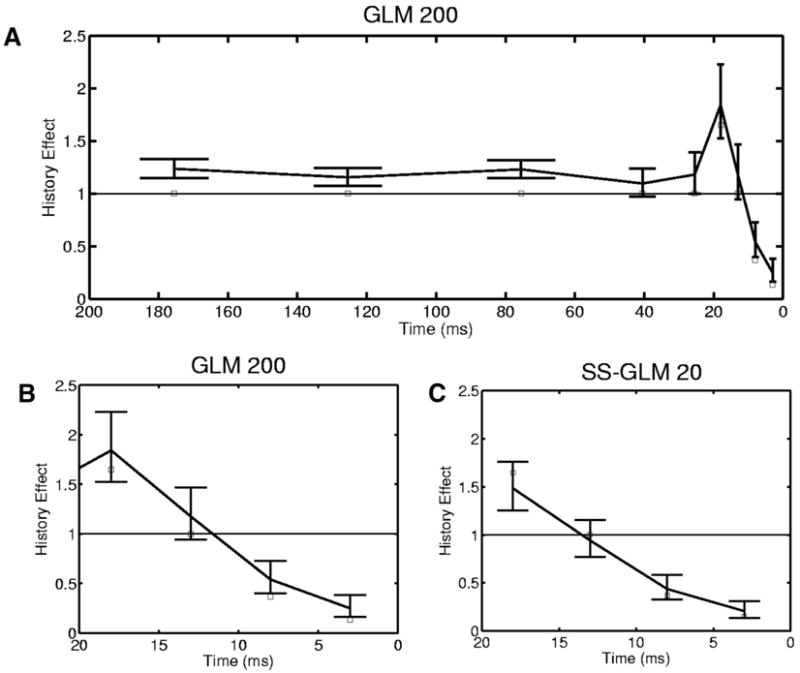
WHAT ARE THE TIMESCALES AND CHARACTERISTICS OF THE NEURON’S INTRINSIC AND NETWORK DYNAMICS?

We examine the spike-history component in detail by plotting the estimate obtained from the GLM 100 (Fig. 14A) and the SS-GLM 100 models (Fig. 14B). The spike-history components of the two models suggest that the neuron has strong absolute refractory (1–5 ms) and relative refractory (6 –10 ms) periods. The spiking propensity of this neuron is not modulated by spiking activity 11 to 20 ms prior to the current time. It also shows a strong positive modulation by spiking activity from 21 to 100 ms prior to the current time that may be due to late intrinsic dynamics and perhaps the effect of network dynamics (Truccolo et al. 2005). The positive modulation of the GLM 100 model is slightly greater than that of the SS-GLM 100 model. These two models demonstrate that this neuron’s spiking activity is strongly modulated by intrinsic and possibly network dynamics. These spike-history modulations of the neural spiking activity cannot be discerned from the standard raster, PSTH, and spike rate plots (Fig. 1).

FIG. 14.

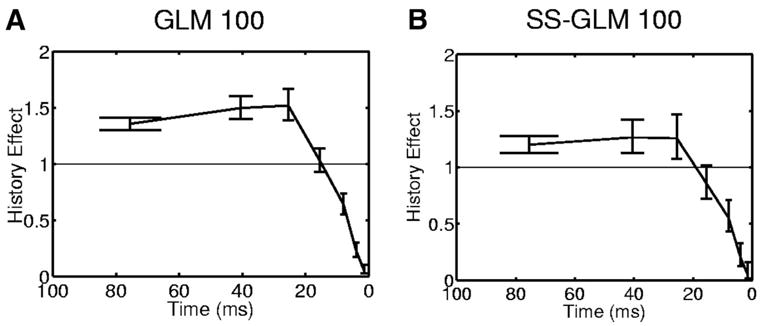
Spike-history component (Eq. 15) for the hippocampal neural spiking activity (Fig. 1) estimated from the GLM 100 (A) and the SS-GLM 100 (B) models along with 95% confidence intervals (bars). The spike-history components of the 2 models were estimated with time bins of 1–2, 3–5, 6 –10, 11–20, 21–30, 31–50, and 51–100 ms.

In conclusion, we see that the SS-GLM analysis provides a highly informative summary of this neuron’s spiking activity that estimates using one model the between-trial and within-trial spiking dynamics that were estimated separately from the SS-PSTH and the GLM 100, respectively. The between-trial dynamics and part of the within-trial dynamics may be interpreted as strong behavioral or learning effects (stimulus- or task-specific modulation), whereas the other component of the within-trial dynamics represents strong intrinsic and possibly network dynamics (spike-history component) of the neuron.

ELECTROPHYSIOLOGICAL PROFILES OF FIVE OTHER HIPPOCAMPAL NEURONS

We use the SS-GLM model to analyze the spiking activity of five other hippocampal neurons recorded from monkeys executing the location-scene association task. The neural responses varied dramatically from very sparse spiking activity (Fig. 15C, column 1) to very intense spiking (Fig. 15E, column 1). The differences in the raster plots are reflected in the differences in the estimated stimulus components for each neuron (Fig. 15, column 2). For each neuron the SS-GLM analysis shows significant spike-history modulation (Fig. 15, column 3). These analyses illustrate that despite the fact that these are the same type of neurons recorded during the same task, the nature of their intrinsic and possibly network dynamics show wide differences. In particular, the timescales and characteristics of the extent to which each of the five neurons depends on its spike history differ appreciably. Neurons B and C show significant decreases in their between-trial or learning components in their experiments, whereas none of the other three neurons shows significant between-trial changes in their activity (Fig. 15, column 4).

FIG. 15.

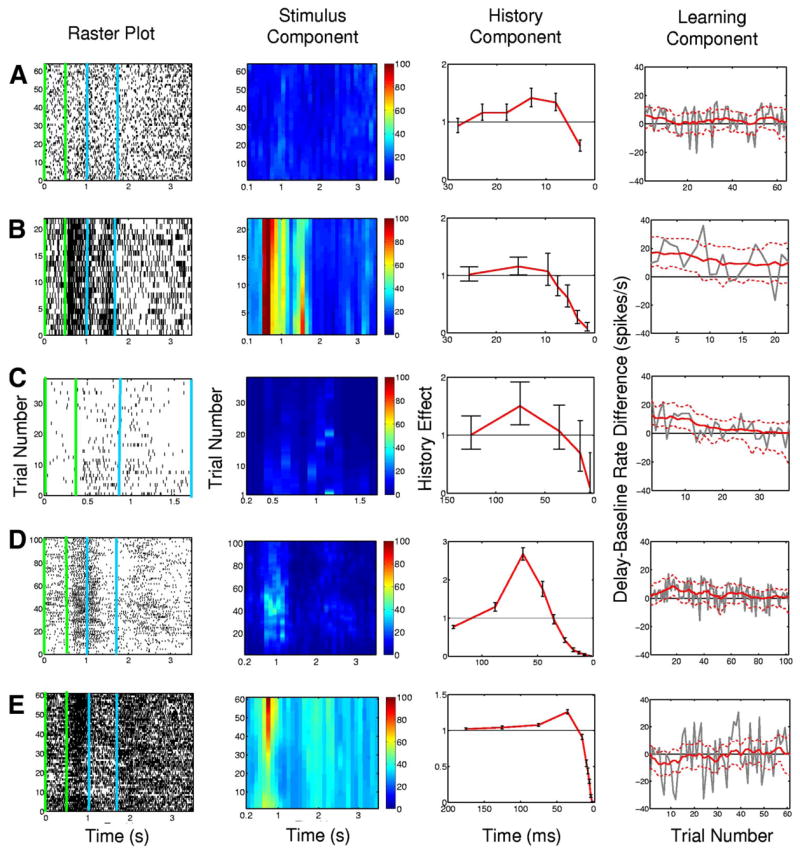
Summary analysis of SS-GLM model fits to spiking activity from five additional hippocampal neurons (rows A–E) recorded from monkeys executing the location-scene association task. The analysis includes the raster plots (column 1), the between-trial and within-trial estimates of the stimulus component (column 2), the spike-history component with 95% confidence intervals (red curve with bars) (column 3) and the learning component (column 4). The green vertical lines and the blue vertical lines in raster plots in column 1 demarcate the baseline period and delay period, respectively. The color scale in column 2 is in spikes/s. The learning component (task-specific activity) was estimated as the within-trial difference between the spike rate between the baseline and delay periods (Eq. 20) as a function of trial number (column 4, red curve). The dashed red lines (column 4) are the 95% confidence intervals and the gray curve is the empirical estimate of the difference in spike rates.

Further details of these analyses may be found at our website (https://neurostat.mgh.harvard.edu/SSGLM).

DISCUSSION

Logic of the state-space generalized-linear model

In developing our state-space generalized-linear model, we believe, as suggested by Dayan and Abbott (2001), that analyses of neural responses should simultaneously characterize the neuron’s stimulus response and its biophysical properties. Spike-triggered average (Schwartz et al. 2006), reverse correlation (Dayan and Abbott 2001), Wiener kernel (Rieke et al. 1997), PSTH (Gerstein 1960), and GLM methods (Brillinger 1988; Brown et al. 2002, 2003, 2004; Harris et al. 2003; Kass and Ventura 2001; Kass et al. 2005; Paninski et al. 2004; Truccolo et al. 2005) have been used to relate neural responses to applied stimuli. Because, in addition, the GLM has been used to relate spiking activity simultaneously to a stimulus, biophysical properties (spike history), and other covariates (Truccolo et al. 2005), we chose it from among these several methods to be the basis for constructing our analysis methods for multiple-trial neurophysiology experiments.

A GLM alone could be successful in predicting single-neuron activity in multiple trial experiments if there were no between-trial changes in either the task-specific or the spike-history effects (Kass et al. 2005; Truccolo et al. 2005). However, in many behavioral experiments, a key objective is to determine whether there is an evolution of the task-specific response between trials because such dynamics provide evidence for important behavioral changes such as learning. Thus to account for between-trial dynamics in the task-specific activity, we developed a state-space extension of the GLM (Eqs. 5 and 6). The state-space formulation captures the evolution of the task-specific activity by allowing the coefficients of the model’s stimulus component (Eqs. 3 and 6) to differ between trials. In this way, the stimulus effect at each trial can be different. We guard against overfitting by imposing the continuity constraint that the coefficients at trial k should be stochastically close to the coefficients at trial k − 1 (Eq. 6). The stimulus component, described at each trial by the linear combinations of unit pulse functions (Eq. 9 and Fig. 2), is not constant, and thus has a within-trial component as well. The other component of the within-trial dynamics is captured by the model’s spike-history component (Eq. 4). It is designed to capture the biophysical properties of the neuron such as the effects on the neuron’s spiking propensity of its absolute and relative refractory periods and possible network dynamics.

The random walk model (Eqs. 3 and 6) provides a simple way to let the coefficients of the stimulus functions be different on different trials subject to a plausible constraint that prevents the parameter estimation problem from becoming intractable. For example, in the actual data example we consider, without the random walk constraint, the number of parameters to be estimated for the stimulus component with the number of basis functions being R = 11 in an experiment with 55 trials would be 11 coefficients/trial × 55 trials = 605 coefficients. Because the coefficients of the between-trial components of the stimulus represented by the random walk model are an unobservable process, we estimated them, along with the model parameters using an EM algorithm (Smith and Brown 2003; Smith et al. 2004, 2005, 2007). We demonstrated how AIC, K-S plots, and ACF analyses can be used to identify the best form of the SS-GLM to approximate the deterministic state-space point process model used to simulate the data. The SS-GLM captured the important features of the stimulus and spike-history components. Our results further showed how the between-trial and within-trial neural spiking dynamics can be identified with the stimulus components of these models and how the spike-history component can be identified with the biophysical properties of the neuron.

Model selection and goodness-of-fit for the actual data analysis

In the analysis of the neural spiking activity from the monkey performing the location-scene association task, the SS-PSTH clearly improved on the PSTH by including a between-trial component. In fact, the SS-PSTH gave a quantitative formulation (Fig. 11C) of the structure seen in the raster plots (Fig. 1A). That is, it provides an estimate of the task-specific effect as a function of trial and time within the trial. The GLM 100 with a PSTH stimulus component gave an appreciably more accurate description of the data that, despite not having an explicit component for between-trial dynamics, improved appreciably on the SS-PSTH in terms of the AIC model selection analysis (Fig. 9) and the K-S plot and ACF goodness-of-fit analyses (Fig. 10). The ability of the GLM 100 to describe the data successfully underscores the importance of the spike history (the neuron’s biophysical properties) in providing an accurate prediction of the neuron’s spiking activity. As a consequence, it was not a surprise that by including a stimulus component that had between-trial and within-trial dynamics and a spike-history component, the SS-GLM improved on both the SS-PSTH and the GLM in terms of the model selection (Fig. 9) and goodness-of-fit (Fig. 10) criteria.

The AIC showed that the SS-GLM 100 provided a better approximating model than the GLM 100 (Fig. 9 and Table 2). However, the fit of the GLM 100 in terms of K-S plots (Fig. 10I, blue curve) appeared to be as good as the fit of SS-GLM 100, even though the GLM 100 modeled the stimulus as a PSTH instead with a between-trial component. The GLM 100 gave a good fit because, although the same coefficients were used to estimate the spike-history component on each trial, a different set of initial spikes was used to start the estimation on each trial (Eq. 4). This is analogous to starting a differential equation from different sets of initial conditions. This feature of the GLM 100 allowed it to estimate implicitly different effects between trials in the absence of an explicit between-trial model component.

Despite this apparently good fit of the GLM 100, several other properties of the GLM 100, in addition to AIC and the ACF, demonstrate why it is not the best approximating model. First, because it had no between-trial model component, the GLM 100 does not provide an explicit estimate of a between-trial or behavior-related effect. Second, simulation of the SS-GLM 100 generated data like those seen in the experiment, whereas simulation of the GLM 100 did not (results not shown). Third, the results from the SS-GLM 100 analysis are robust in the sense that a model estimated on just the odd trials predicted very well the spiking activity on the even trials and vice versa in terms of K-S plots and ACF analyses (results, not shown). Also, the estimates of the stimulus and spike-history model components are nearly identical to those estimated from the full data set. This was not true for the GLM 100. Finally, it was not possible with either the SS-GLM 100 or the GLM 100 to predict the spiking activity at trials 28 to 55 from that in trials 1 to 27 or vice versa, confirming the importance of between-trial dynamics across the entire experiment. These results demonstrate the importance of using multiple measures of goodness-of-fit and of checking the descriptive and predictive properties of models that have apparently good fits to assess the validity of the approximations.

Answering neurophysiological questions

Standard questions asked in analyses of multiple-trial neurophysiological experiments include: Does a neuron have task-specific activity? What is the nature of the stimulus or task-specific activity between trial and within trial? In learning experiments, is there evidence of learning-related neural dynamics? These three questions are all related yet, in current analyses, the first is answered with ANOVA; the second with raster plots, ANOVA, and the PSTH; and the third by plotting spike rates across trials. The most compelling feature of our SS-GLM analysis is its ability to give detailed, quantitative answers to all of these neurophysiology questions from the estimated stimulus component of our model. This is because our model captures the rich between-trial and within-trial structure readily apparent in the raster plots. Our inference framework allows us to ask specific questions about this structure and other features of the data in a way that is more appropriate than the Gaussian-based framework associated with ANOVA or the Poisson-based analyses commonly used with the PSTH. The SS-GLM analysis obviates the problem of multiple hypothesis tests or the use of techniques to correct for multiple hypothesis tests by estimating the joint distribution of the stimulus components. By so doing, we actually conduct an empirical Bayes’ analysis of the neuron’s response to the stimulus rather than conducting formal hypothesis tests (Carlin and Louis 2001). Our results (Figs. 11–15) demonstrate that our approach leads to far more informative analyses than current methods.

As reported in previous GLM analyses (Truccolo et al. 2005), the spike-history component of our model readily identifies short-, intermediate-, and long-timescale biophysical properties of the neuron (Fig. 14). These important properties are not considered in the current analyses of multiple-trial experiments. Moreover, they cannot be deduced from any of the standard plots or analyses of these data (Fig. 1). We showed that these biophysical properties can be quite different even for neurons recorded in the same experiment (Fig. 15). Studies of the differences in these biophysical properties of the neurons may provide a new dimension along which to characterize the properties of the neural response. The model selection (Fig. 9) and the goodness-of-fit (Fig. 10) analyses for the GLM 100 also showed that these biophysical properties can be of equal or greater importance than the stimulus component in predicting the spiking activity of a neuron. Therefore their simultaneous estimation along with the stimulus- or task-specific component of the model is crucial for correctly identifying the appropriate magnitude of the neuron’s stimulus response. Finally, the strength of the spike-history component in the data from all six of the neurons analyzed here demonstrates that the spiking activity of these neurons is highly non-Poisson because, in a Poisson model, spiking activity is independent of history. Furthermore, the spike-history component of our model makes explicit that the spike rate determines spiking activity and that previous spiking activity affects the current spike rate. Therefore future instantiations of the SS-GLM may offer new insights into the rate versus temporal code debate in neuroscience (Shadlen and Newsome 1994; Victor 1999).

Extensions and future work

To establish what new neurophysiological insights can be gained from our new methods, a detailed study of all of the neurons recorded in the location-scene association task (Wirth et al. 2003) will be the topic of a future report. In addition, we are investigating two extensions of the current work: extensions of the model and extensions of the estimation procedures. First, we chose unit pulse functions (Fig. 2) to model the stimulus so that the PSTH would be a special case of our SS-GLM. We can replace these functions with any other functions deemed appropriate to model the structure in the stimulus. Second, in addition to behavioral experiments, many other types of neuroscience experiments record the responses of single neurons to repeated applications of the same stimulus. For example, these include light for retinal neurons, odors for olfactory neurons, and sounds for auditory neurons. We can extend the stimulus component of the model to include analyses of stimuli in these experiments. Wiener kernel methods are often used to model the stimulus–response relation for these stimuli (Rieke et al. 1997). Third, the stimulus component of the model can also be easily modified to include other covariates that are simultaneously recorded with the application of a stimulus such as spiking activity of other neurons (Truccolo et al. 2005) and local field potentials. Fourth, our current state-space model uses the most rudimentary form possible to describe the between-trial dynamics: a random walk model. Thus a fifth important extension of the current model would be to develop more complex state-space representations guided both by more detailed hypotheses about the between-trial neural dynamics and by use of the model selection and goodness-of-fit techniques to evaluate formally the significance of the new formulations. Similarly, if deemed appropriate, the between-trial dynamics can be extended in a straightforward manner to include the spike-history component of the model. This could allow characterization of another aspect of the neuron’s plasticity on perhaps a faster timescale (Frank et al. 2004). Finally, an alternative form of the state-space model could also be a way to incorporate other types of dynamics such as cortical up– down states (Haslinger et al. 2006; Ji and Wilson 2007).

The use of the EM algorithm to perform the model fitting by maximum likelihood can be extended to Bayesian estimation by formulating prior distributions for the model parameters. Successful extensions of the EM algorithm methods for fitting state-space models to behavioral data to Bayesian approaches using the Bayesian Analysis Using Gibbs Sampling (BUGS) program have been recently reported (Smith et al. 2007). A key advantage of this extension is that each change of the model does not require writing a new EM fitting algorithm as is presently the case with any changes in the SS-GLM. Finally, the view of the model fitting as an L² regularization problem (Eq. 7) suggests that for other neural systems other types of regularization, such as L¹ regularization (Hastie et al. 2003), may be more appropriate and could be used as alternatives. These extensions will be the topics of future reports.

The Matlab software used to implement the methods presented here is available at our website (https://neurostat.mgh. harvard.edu/SSGLM/MatlabCode).

APPENDIX A

Derivation of the EM algorithm

We use an EM algorithm to find the maximum-likelihood estimates of ψ = (γ, θ₀, Σ). This requires us to maximize the expectation of the complete data log-likelihood (Dempster et al. 1977). The complete data likelihood is the joint probability density of N and θ, which for our model is

$$\begin{array}{l}p(\theta ,N\mid \psi )=p(N\mid \theta ,\psi )\times p(\theta \mid \psi )\\ =exp\left\{\sum _{k=1}^K\sum _{\ell =1}^L{n}_{k\ell }log[{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\mathrm{\Delta }]-{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\mathrm{\Delta }\right\}\\ \times {[{(2\pi )}^{-R/2}\mid \mathrm{\sum }{\mid }^{-1/2}]}^K\\ \times exp\left\{-2^{-1}\sum _{k=1}^K({\theta }_k-{\theta }_{k-1}{)}^{\prime }{\mathrm{\sum }}^{-1}({\theta }_k-{\theta }_{k-1})\right\}\end{array}$$ (A1)

where the first term on the right-hand side of the Eq. A1 is the joint probability mass function of a point process characterized by a conditional density function λ_k(ℓΔ|θ_k, γ, H_k,ℓ) (Eq. 5). The second term is the joint probability density of the unobservable state process defined by the Gaussian random walk model in Eq. 6. An EM algorithm is an iterative procedure for computing maximum-likelihood estimates (Dempster et al. 1977). Each iteration consists of two steps: an Expectation or E-step and a Maximization or M-step. At iteration i + 1 of the algorithm, we compute in the E-step the expectation of the complete data log-likelihood given N, the spiking activity in all of the trials, the parameter estimates, ${\psi }^{(\text{i})}=[{\gamma }^{(\text{i})},{\theta }_0^{(i)},{\mathrm{\sum }}^{(i)}]$ from iteration i. The expectation of the complete data log-likelihood is defined as follows

E-Step

$$\begin{array}{l}Q(\psi \mid {\psi }^{(i)})=E[\sum _{k=1}^K\sum _{\ell =1}^L{n}_{k,\ell }log[{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\mathrm{\Delta }]\\ -{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\mathrm{\Delta }\Vert N,{\psi }^{(i)}]-2^{-1}\mathit{KR}log(2\pi )-2^{-1}Klog\mid \mathrm{\sum }\mid \\ -2^{-1}E\left[\sum _{k=1}^K({\theta }_k-{\theta }_{k-1}{)}^{\prime }{\mathrm{\sum }}^{-1}({\theta }_k-{\theta }_{k-1})\Vert N,{\psi }^{(i)}\right]\end{array}$$ (A2)

where E[· || N, ψ⁽ⁱ⁾] denotes the expectation of the indicated quantity taken with respect to the probability density of θ given N and ψ⁽ⁱ⁾. On expanding the terms in Eq. A2, we see that computing the expected value of the complete data log-likelihood requires us to evaluate the expected value of the unobserved process θ_k|_K ≡ E[θ_k || N, ψ⁽ⁱ⁾], the covariances W_k,k+1|K ≡ Cov[θ_k, θ_k+1||N, ψ⁽ⁱ⁾], $E[{\theta }_k^2\parallel N,{\psi }^{(\text{i})}]$, and the expected value of the exponential function of the unobserved process, E[exp(θ_k) || N, ψⁱ⁾]. The notation k|k′ denotes the expectation of the unobserved process at trial k given N_1:k′, the spiking activity in trial 1 to trial k′. To compute these quantities we combine three algorithms: a filter algorithm to compute θ_k|K ≡ E[θ_k || N_1:k, ψ⁽ⁱ⁾] and W_k|k ≡; a fixed-interval smoothing algorithm to compute θ_k|K and W_k|K; and a state-space covariance algorithm to compute W_{k,k+ 1|K} (Smith and Brown 2003). The algorithms are as follows.

E-Step I: filter algorithm

A recursive linear filter algorithm for computing θ_k|K and W_k|K is given as (Eden et al. 2004)

$${\theta }_{k\mid k-1}={\theta }_{k-1\mid k-1}$$

$$W_{k\mid k-1}=W_{k-1\mid k-1}+\mathrm{\sum }$$

$$\begin{array}{l}{\theta }_{k\mid k}={\theta }_{k\mid k-1}+W_{k\mid k}\sum _{\ell =1}^L{\lambda }_k{(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })}^{-1}\\ \times \frac{\partial {\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })}{\partial \theta }[n_{k,\ell }-{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\mathrm{\Delta }]{\mid }_{\theta ={\theta }_{k\mid k-1}}\end{array}$$

$$\begin{array}{l}{W}_{k\mid k}=-[-W_{k\mid k-1}^{-1}+\sum _{\ell =1}^L\{{\nabla }^{2}log{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\\ \times [n_{k,\ell }-{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\mathrm{\Delta }]\\ -\nabla log{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\nabla {\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_k,\gamma ,H_{k,\ell })\mathrm{\Delta }\}{\mid }_{\theta ={\theta }_{k\mid k-1}}{]}^{-1}\end{array}$$

for k = 1, …, K. We evaluate the quantities in the following order: θ_{k|k − 1}, W_{k|k − 1}, W_k|k, and θ_k|k. Because the initial condition is a constant vector θ₀, we have θ_1|0 = θ₀, W_0|0 = 0. The filter algorithm provides a sequential Gaussian approximation to the posterior density and the one-step prediction density for our state-space model in Eqs. 5 and 6 (Eden et al. 2004; Smith and Brown 2003).

E-Step II: fixed-interval smoothing algorithm

Given the estimates θ_k|k and W_k|k, we use the fixed-interval smoothing algorithm to compute θ_k|K and W_k|K. This algorithm is (Mendel 1995; Smith and Brown 2003)

$${\theta }_{k\mid K}={\theta }_{k\mid k}+A_k({\theta }_{k+1\mid K}-{\theta }_{k+1\mid k})$$

$$A_k=W_{k\mid k}{W}_{k+1\mid k}^{-1}$$

$$W_{k\mid K}=W_{k\mid k}+A_k(W_{k+1\mid K}-W_{k+1/k})A_k^{\prime }$$

for k = K − 1, …, 1 and the initial conditions θ_K|K and W_K|K. We compute $E[{\theta }_k^2\parallel N,{\psi }^{(\text{i})}]=W_{k\mid K}+{\theta }_{k\mid K}^{\prime }{\theta }_{k\mid K}$.

E-Step III: state-space covariance algorithm

The covariance estimate, Cov [θ_k, θ_u|N, ψ⁽ⁱ⁾] can be computed by using the state-space covariance algorithm (deJong and MacKinnon 1988) as

$$W_{k,u\mid K}=\mathit{Cov}[{\theta }_k,{\theta }_u\parallel N,{\psi }^{(i)}]=A_k\mathit{Cov}[{\theta }_{k+1},{\theta }_u\parallel N,{\psi }^{(i)}]$$

for 1 ≤ k ≤ u ≤ K. We have that W_{k,k+ 1|K} is computed by taking u = k + 1. The other covariances for which u ≠ k + 1 are used to compute the complete joint distribution of the unobserved state process in APPENDICES B through F.

Finally, we need to evaluate the term

$$E[{\lambda }^S(\ell \mathrm{\Delta }\mid {\theta }_k)\parallel N,{\psi }^{(i)}]=E\left[exp\left\{\sum _{r=1}^R{\theta }_{k,r}{g}_r(\ell \mathrm{\Delta })\right\}\Vert N,{\psi }^{(i)}\right]$$

This can be accomplished by expanding exp(θ_k,r) in a Taylor series about θ_k|K,r and taking the expected value to obtain the approximation (Smith and Brown 2003)

$$E[exp({\theta }_{k,r})\parallel N,{\psi }^{(i)}]\doteq exp({\theta }_{k\mid K,r})+2^{-1}exp({\theta }_{k\mid K,r})W_{k\mid K,r,r}$$

where θ_k|K,r is the rth element of θ_k|K and W_k|K,r,r is the rth diagonal element of the matrix W_k|K. To evaluate the expectation we use the fact that θ_k is approximately a Gaussian random vector with mean θ_k|K and covariance matrix W_k|K.

M-Step

In the M-step, we maximize the expected value of the complete data log likelihood (Eq. A2) with respect to the parameter vector ψ = (γ, θ₀, Σ). In so doing, we obtain new iterates ${\psi }^{(i+1)}=[{\gamma }^{(i+1)},{\theta }_O^{(i+1)},{\mathrm{\sum }}^{(i+1)}]$. There is no closed form solution for ${\gamma }^{(i+1)}={\gamma }_1^{(i+1)},\dots ,{\gamma }_J^{(i+1)}$; thus we use a Newton–Raphson algorithm (Fahrmeir and Tutz 2001) to find γ^{(i + 1)} as the solution to

$$\begin{array}{l}{\gamma }_{m+1}^{(i)}={\gamma }_m^{(i)}-{[{\nabla }^{2}Q({\gamma }_m^{(i)},{\theta }_0^{(i)},{\mathrm{\sum }}^{(i)}\mid {\psi }^{(i)})]}^{-1}\\ \times \nabla Q[{\gamma }_m^{(i)},{\theta }_0^{(i)},{\mathrm{\sum }}^{(i)}\mid {\psi }^{(i)}]\end{array}$$ (A3)

where ${\gamma }_m^{(i)}$ is the mth iterate of Newton–Raphson algorithm at the ith iteration of the EM algorithm and ∇ (∇²) is the first (second) partial derivative with respect to vector γ. The initial value ${\gamma }_O^{(i)}$ is set equal to γ ⁽ⁱ⁾, the estimate from the previous EM iteration. When the absolute value of the difference of the consecutive iterates, $\mid {\gamma }_{m+1}^{(i)}-{\gamma }_m^{(i)}\mid$ changes <10⁻² in all J elements, we stop the Newton–Raphson iterations and take ${\gamma }^{(\text{i}+1)}={\gamma }_{m+1}^{(i)}$. The other parameter updated in the M-step is $\mathrm{\sum }=\mathit{diag}\{{\sigma }_1^2,\dots ,{\sigma }_R^2\}$. The closed form solution that maximizes the expected value of the complete data log-likelihood with respect to Σ is

$${\mathrm{\sum }}^{(i+1)}=\frac{1}{K}\sum _{k=1}^{K}E[({\theta }_k-{\theta }_{k-1})({\theta }_k-{\theta }_{k-1}{)}^{\prime }\parallel N,{\psi }^{(i)}]$$ (A4)

for r = 1, …, R and k = 1, …, K. Choosing as the basis functions for the model in Eq. 5 the unit pulse functions (Eq. 9) makes all of the off-diagonal elements of Σ^{(i+ 1)} zero. The last parameter updated in M-step is the initial value of the unobserved state process, θ₀ = (θ_0,1, …, θ_0,R). Its closed form solution is

$${\theta }_0^{i+1}=E[{\theta }_1\parallel N,{\gamma }^{(i)},{\theta }_0^{(i)},{\mathrm{\sum }}^{(i)}]$$ (A5)

For the AIC comparisons (see METHODS) we need to evaluate the observed data log-likelihood, log P(N|ψ̂). To do so we note that because P[N|ψ^{(i+ 1)}] = P[θ, N|ψ^{(i+ 1)}]/P[θ |N, θ^{(i + 1)}], it follows that log P(N|ψ) = log P(θ, N|ψ) − log P(θ|N, ψ) and that (Hastie et al. 2001)

$$\begin{array}{l}logp[N\parallel {\psi }^{(i+1)}]=E[logP(\theta ,N\parallel {\psi }^{(i+1)})\mid N,{\psi }^{(i)}]\\ -E[logP(\theta \parallel N,{\psi }^{(i+1)})\parallel N,{\psi }^{(i)}]\\ =Q[{\psi }^{(i+1)}\mid {\psi }^{(i)}]-R[{\psi }^{(i+1)}\mid {\psi }^{(i)}]\end{array}$$ (A6)

Because the random variable θ|N, ψ⁽ⁱ⁾ is approximately Gaussian with mean θ⁽ⁱ⁾ = E[θ|N, ψ⁽ⁱ⁾] and covariance W⁽ⁱ⁾ = Cov [θ|N, ψ⁽ⁱ⁾] computed in the E-step of ith EM iteration, it follows that

$$\begin{array}{l}R[{\psi }^{(i+1)}\mid {\psi }^{(i)}]\\ =-2^{-1}\mathit{KR}log(2\pi )-2^{-1}log\parallel W^{(i)}\mid \\ =-2^{-1}tr[W^{(i)}{(W^{(i+1)})}^{-1}]-2^{-1}[{\theta }^{(i+1)}-{\theta }^{(i)}{]}^{\prime }{[W^{(i)}]}^{-1}[{\theta }^{(i+1)}-{\theta }^{(i)}]\end{array}$$

At the last EM iteration ψ^{(i + 1)} is the maximum-likelihood estimate of ψ and we have that R[ψ^{(i + 1)}|ψ⁽ⁱ⁾] is approximately

$$R[{\psi }^{(i+1)}\mid {\psi }^{(i)}]\approx -2^{-1}\mathit{KR}log(2\pi )-2^{-1}log\mid W^{(i)}\mid -2^{-1}\mathit{KR}$$ (A7)

The details on how to accelerate this EM algorithm are given on our website (https://neurostat.mgh.harvard.edu/SSGLM/MatlabCode).

APPENDIX B

Approximation of the joint distribution of the unobserved state process

We approximate the probability density p(θ₁, …, θ_K|N, ψ̂) by the Gaussian probability density with mean (θ_1|K, …, θ_K|K) and covariance

$$W=\left[\begin{array}{cccc}{W}_{1\mid K}& W_{1,2\mid K}& \cdots & W_{1,K\mid K}\\ W_{2,1\mid K}& W_{2\mid K}& \cdots & W_{2,K\mid K}\\ \cdots & \cdots & \cdots & \cdots \\ W_{K,1\mid K}& W_{K,2\mid K}& \cdots & W_{K\mid K}\end{array}\right]$$ (B1)

where the θ_1|K, …, θ_K|K are R × 1 vectors and W_k|_K and W_{k,k′ = 1,…,K} are R × R matrices defined in the last iteration of EM algorithm. To draw a random sample from a multivariate Gaussian distribution with mean θ_1|K, …, θ_K|K and a nondiagonal covariance matrix W we use the Cholesky decomposition of the covariance matrix W (Gentle 1998). If the basis functions in Eq. 5 are unit pulse functions (Eq. 9), then the random vectors (θ_1,r, …, θ_K,r), r = 1, …, R, are independent, whereas the components of each vector (θ_1,r, …, θ_K,r) are not independent. Therefore to draw a random sample from p(θ₁, …, θ_K|N, ψ̂) we draw R independent random samples.

APPENDIX C

Standard errors for the EM estimates of the parameters

The asymptotic covariance matrix for the maximum likelihood ψ̂ = (γ̂, θ₀^ Σ^) is the inverse of the expected information matrix. Thus we can approximate Var (ψ̂) as I⁻¹(ψ̂|N). From McLachlan and Krishnan (1997) it follows that

$$\begin{array}{l}I(\widehat{\psi };N)=I_c(\widehat{\psi };N)-I_m(\widehat{\psi };N)=E_{\widehat{\psi }}\left[-\frac{{\partial }^{2}logp(\theta ,N\mid \psi )}{\partial \psi \mid {\psi }^{\prime }}\mid N\right]\\ -E_{\widehat{\psi }}\left[\left(\frac{\partial logp(\theta ,N\mid \psi )}{\partial \psi }\right){\left(\frac{\partial logp(\theta ,N\mid \psi )}{\partial \psi }\right)}^{\prime }\mid N\right]\end{array}$$ (C1)

where p(θ, N|ψ) is the complete data likelihood (Eq. A1). The first term on the right side of Eq. C1 contains terms of the form E[θ_kθ_{k − 1}|N, ψ̂], which can be easily evaluated from the EM algorithm calculations already performed. We evaluate the second term using a Monte Carlo algorithm as follows:

1. For r = 1, …, R draw a random sample of size M_c from a Gaussian distribution with mean vector (θ_1,r|K, …, θ_K,r|K) and covariance matrix W (APPENDIX B). Denote the draws as $({\theta }_{1,r}^c,\dots ,{\theta }_{K,r}^c)$, for c = 1, …, M_c. Further, let

   $${\theta }^c-\left[\begin{array}{ccc}{\theta }_{1,1}^c& \cdots & {\theta }_{1,R}^c\\ ⋮& & ⋮\\ {\theta }_{K,1}^c& \cdots & {\theta }_{K,R}^c\end{array}\right]$$

2. For every c compute

   $$S_c=\frac{\partial logp({\theta }^c,N\mid \widehat{\psi })}{\partial \psi }$$

3. Take $M_c^{-1}{\sum }_{c=1}^{M_c}{S}_c{S}_c^{\prime }$ as an estimate of I_m(ψ̂|N).

In our analyses we use M_c = 100.

APPENDIX D

Constructing confidence intervals for the stimulus component

A Monte Carlo algorithm for computing K × L simultaneous confidence intervals for the stimulus effect, λ^S(ℓΔ|θ_k), and at time ℓΔ trial k (Eq. 3), is as follows:

1. For r = 1, …, R draw a random sample of size M_c from a Gaussian distribution with mean vector (θ_1,r|K, …, θ_K,r|K) and covariance matrix W (APPENDIX B). Denote the draws as $({\theta }_{1,r}^c,\dots ,{\theta }_{K,r}^c)$, for c = 1, …, M_c.

2. For every sample c, trial k, and time bin ℓ, compute ${\lambda }^c=exp\{{\sum }_{r=1}^R{\theta }_{k,r}^c{g}_r(\ell \mathrm{\Delta })\}$, where c = 1, …, M_c; k = 1, …, K; and ℓ = 1, …, L.

3. For every k and ℓ order the values λ^c from the smallest to the largest and denote the ordered values as λ^c.

4. The 100(1 − α)% confidence interval for λ^S(ℓΔ|θ_k) is [λ^(c′), λ^(c″)], for k = 1, …, K, where λ^(c′) and λ^(c″) are defined such that α/2 = c′/M_c and 1 − (α/2) = c″/M_c for α ∈ (0, 1).

Choosing α = 0.05 yields 95% confidence intervals. In our analyses we take M_c = 3,000.

APPENDIX E

Constructing confidence intervals for functions of the spike rate

We compute simultaneous confidence intervals for the true spike rate function Eq. 16 and the true difference in spike rate functions defined in Eq. 19. We refer to the two functions as h(ψ; θ_k). The K confidence intervals for h(ψ; θ_k) can be obtained by the following Monte Carlo algorithm:

1. For r = 1, …, R draw a random sample of size M_c from a Gaussian distribution with mean vector (θ_1,r|K, …, θ_K,r|K) and covariance matrix W (APPENDIX B). Denote the draws as $({\theta }_{1,r}^c,\dots ,{\theta }_{K,r}^c)$, for c = 1, …, M_c.

2. For every sample c and trial k compute $h^c=h(\widehat{\psi };{\theta }_{k,1}^c,\dots ,{\theta }_{k,R}^c)$, where c = 1, …, M_c, k = 1, …, K.

3. For every k order the values h^c from the smallest to the largest and denote the ordered values as h^(c).

4. The 100(1 − α)% confidence band for h(ψ; θ_k), is [h^(c′), h^(c″)] for k = 1, …, K, where h^(c′) and h^(c″) are such that α/2 = c ′/M_c and 1 − (α/2) = c ″/M_c for α ∈ (0, 1).

Choosing α = 0.05 yields 95% confidence intervals. In our analyses we take M_c = 300.

APPENDIX F

Between-trial comparisons for the spike rate

We show how to evaluate Pr [(t₂ −t₁)⁻¹ Λ̂_m(t₁, t₂) > (t₂− t₁)⁻¹ Λ̂_k(t₁, t₂)] in Eq. 18, for any k = 1, …, K − 1, m > k. As in Smith et al. (2005), we estimate the K × K matrix of these probabilities using Monte Carlo methods. The algorithm is as follows.

1. For r = 1, …, R draw a random sample of size M_c from a Gaussian distribution with mean vector (θ_1,r|K, …, θ_K,r|K) and covariance matrix W (APPENDIX B). Denote the draws as $({\theta }_{1,r}^c,\dots ,{\theta }_{K,r}^c)$, for c = 1, …, M_c.

2. For every sample c and trial k compute $h_k^c={(t_2-t_1)}^{-1}{\sum }_{\ell ={\ell }_1}^{{\ell }_2}{\lambda }_k(\ell \mathrm{\Delta }\mid {\theta }_{k,[\ell /R]}^c,\dots ,{\theta }_{K,[\ell /R]}^c,\widehat{\gamma },H_{k\mid \text{u}})\mathrm{\Delta }$, where c = 1, …, M_c, k = 1, …, K.

3. For every pair of trials m, k, m > k, m = 1, …, K, k = 1, …, K let S_Mc be the number of cases for which $h_m^c>h_k^c$.

4. For each m, k pair such that m > k, we estimate Pr [(t₂ − t₁) ⁻¹ Λ̂_m(t₁, t₂) > (t₂ − t₁)⁻¹ Λ̂_k(t₁, t₂)] as $M_c^{-1}{S}_{M_c}$.

In our analyses we use M_c = 300.