FIG. 9.

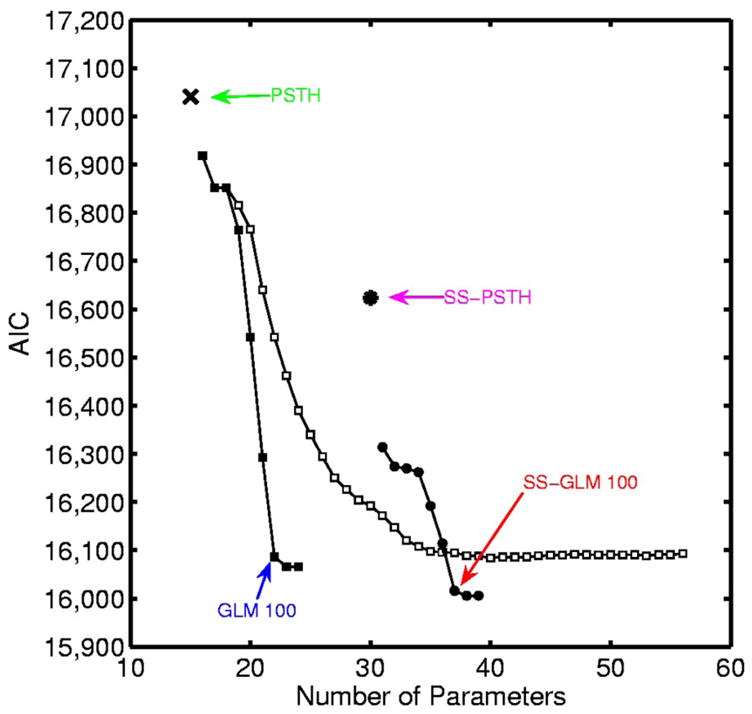
AIC for the analysis of the hippocampal neural spiking activity (Fig. 1) plotted as a function of the number of parameters for the candidate models: PSTH (×), GLM with coarse binning (black squares), SS-PSTH (asterisk), GLM with fine binning (open squares), and SS-GLM with coarse binning (black circles). The model with the smallest AIC value provides the best approximating model. The number of parameters is p, the dimension of ψ = (γ, θ₀, Σ) in Eq. 13. We construct the spike-history components of the GLM models (Eq. 4) by considering spike dependence going back 200 ms using coarse time binning and fine time binning. The coarse time bins are 1–2, 3–5, 6 –10, 11–20, 21–30, 31–50, 51–100, 101–150, and 151–200 ms. For the fine time binning the first 2 bins are 1–2 and 3–5 ms, whereas from 5 to 200 ms, we divide time into 39 bins each 5 ms in width. The best approximating model among the nonstate-space GLM models used coarse history dependence ≤ 100 ms defined as bins: 1–2, 3–5, 6 –10, 11–20, 21–30, 31–50, and 51–100 ms (GLM 100, blue). The best approximating model among all the models considered was the SS-GLM model also with a 100-ms coarse history dependence (SS-GLM 100, red). The model fits of the PSTH (green), GLM 100 (blue), SS-PSTH (pink), and SS-GLM 100 (red) are summarized in Table 2.