Abstract
In fMRI data analysis it has been shown that for a wide range of situations the hemodynamic response function (HRF) can be reasonably characterized as the impulse response function of a linear and time invariant system. An accurate and robust extraction of the HRF is essential to infer quantitative information about the relative timing of the neuronal events in different brain regions. When no assumptions are made about the HRF shape, it is most commonly estimated using time windowed averaging or a least squares estimated general linear model based on either Fourier or delta basis functions. Recently, regularization methods have been employed to increase the estimation efficiency of the HRF; typically these methods produce more accurate HRF estimates than the least squares approach (Goutte, et al. 2000). Here, we use simulations to clarify the relative merit of temporal regularization based methods compared to the least squares methods with respect to the accuracy of estimating certain characteristics of the HRF such as time to peak (TTP), height (HR) and width (W) of the response. We implemented a Bayesian approach proposed by Marrelec et al. (2001, 2003) and its deterministic counterpart based on a combination of Tikhonov regularization (Tikhonov and Arsenin 1977) and generalized cross-validation (GCV) (Wahba,1990) for selecting the regularization parameter. The performance of both methods is compared with least square estimates as a function of temporal resolution, color and strength of the noise, and the type of stimulus sequences used. In almost all situations, under the considered assumptions (e.g. linearity, time invariance and smooth HRF), the regularization-based techniques more accurately characterize the HRF compared to the least-squares method. Our results clarify the effects of temporal resolution, noise color, and experimental design on the accuracy of HRF estimation.
Keywords: Event-related fMRI, HRF estimation, Tikhonov regularization, GCV
Introduction
Event-related functional magnetic resonance imaging (ER-fMRI) data analysis is typically based on the assumption that the Blood Oxygen Level Dependent (BOLD) signal (Ogawa, et al. 1990) is the output of a linear and time invariant system (Boynton, et al. 1996; Friston, et al. 1994). While nonlinearities in the BOLD response have been documented (Boynton, et al. 1996; Buxton, et al. 1998; Dale and Buckner 1997) the assumption of linearity has been shown to be a good approximation in a wide range of situations (Friston, et al. 1998; Glover 1999). Here we have assumed that the fMRI time series is the convolution of the HRF with a given stimulation pattern. Despite recent and impressive progress (Logothetis and Pfeuffer 2004) the relationship between the fMRI signal and neuronal activity is not well understood, an accurately estimated HRF at each voxel can provide potentially useful quantitative information about the relative timing and the response amplitude of neuronal events under various experimental manipulations. Due to regional variability in the blood flow response, care must be used if one is interested in comparing BOLD time courses across brain regions (Lindquist and Wager 2007; Menon, et al. 1998; Miezin, et al. 2000). Although, it has been shown that time course differences between primary visual cortex and supplementary motor area are predictive of response time in a visual-motor task (Menon, et al. 1998).
Estimation methods differ in the assumptions they make about the underlying shape of the HRF. In this work, we will focus our attention on methods that do not assume a fixed shape of the HRF in order to account for its variability across brain regions and subjects (Aguirre, et al. 1998; Handwerker, et al. 2004). The HRF can be estimated by modeling the fMRI time series using the general linear model (Friston, et al. 1995) and a set of delta functions, which is an approach commonly known as the finite impulse response (FIR) method (Dale 1999; Lange, et al. 1999). In this case the design matrix contains as many columns as HRF values being estimated. The first column is a vector of ones and zeros that represents the event onset times (in an ER-experiment) locked to the acquisition times and the rest of the columns are its temporally shifted versions. This approach has been applied by several researchers to estimate the HRF in different applications (Lu, et al. 2006; Lu, et al. 2007; Miezin, et al. 2000; Ollinger, et al. 2001a; Ollinger, et al. 2001b; Serences 2004).
There is considerable evidence suggesting that the HRF is smooth (Buxton, et al. 2004) and several researchers have used this property as a physiologically meaningful constraint in their HRF estimation schemes. Goutte et al. (2000) proposed the use of the smooth FIR (or temporal regularization) by combining the temporal smoothness constraint on the HRF with boundary conditions. They used a Bayesian approach based on Gaussian priors on the HRF with a covariance structure that they showed to be equivalent to constraining a high order discrete derivative operator. A similar conceptual line was followed by Marrelec et al. (2001, 2003), but in this case the second derivative discrete operator was used to impose smoothness on the estimated HRF. In a more sophisticated development, the method was extended to deal with multiple event designs, variability across sessions, and HRF temporal resolution shorter than the actual temporal resolution of the collected data (Ciuciu, et al. 2003). In addition, two approaches based on Tikhonov regularization (Tikhonov and Arsenin 1977) and generalized cross validation (GCV) (Wahba 1990) have been introduced for HRF estimation. The Tikhonov-GCV (Tik-GCV) method has a long history in the inverse problems literature, but has been rarely applied to fMRI data. Zhang et al. (2007) proposed a two level algorithm to estimate not only the HRF but the drift using smoothness constraints. To estimate the regularization parameter at each level they used GCV and Mallow's Cp criteria. Vakorin et al. (2007) have used Tikhonov regularization based on B-spline basis and a GCV for selection of the regularization parameter. Their approach was customized for block-designs.
In this paper we simulate event-related fMRI designs to study the impact of temporal regularization based methods on the estimation of HRF features such as time to peak (TTP), height of the response (HR) and the width of the response (W) when compared to the more common least squares or maximum likelihood estimation. We implemented the Bayesian method proposed by Marrelec et al (2001,2003) and its deterministic counterpart based on Tikhonov regularization combined with generalized cross-validation for the selection of the regularization parameter. Although our Tik-GCV algorithm is related to previous work (Vakorin, et al. 2007; Zhang, et al. 2007), our approach focuses on using delta basis functions to estimate the HRF during ER-designs and it consists of only one step. Our approach is more similar to the Bayesian approach of Marrelec et al. (2001, 2003) but it differs on the critical issue of how the regularization parameter is selected. In our simulations, we use different probabilistic distributions of the inter-trial-intervals (ITI) (Hagberg, et al. 2001), different temporal resolutions, and vary the color and power of the noise. The performance of each technique is then illustrated using real data.
Materials and Methods
Linear Model
If we assume that the fMRI response is linear and time invariant then the BOLD signal y at a given voxel can be represented as
| (1) |
where y is a N × 1 vector representing the fMRI signal from a voxel, N is the number of time samples, X = [X1X2…X Ne], where Xi is the stimulus convolution matrix (with dimension N × Ns) corresponding to the event i, h is a NsNe × 1 vector containing the vertical concatenation of the individual HRFs and Ne is the number of events. The stimulus convolution matrix Xi is generated based on the stimulus sequence. The dimension Ns of the vector hi (i-th event HRF) is determined by the assumed duration of the HRF and its discretization time resolution. Finally, n is additive noise with covariance matrixV.
In this work we model the drift usually observed in the fMRI times series using orthogonal polynomials, the number of events was set to Ne = 1 and the noise was considered to be i.i.d Gaussian (V = I). In order to account for the autocorrelation present in the fMRI time series, the temporal covariance structure should be estimated based on the acquired data (Friston, et al. 2002; Worsley, et al. 2002) and used to pre-whiten the fMRI time series before applying the model. So, our linear model will be defined as
| (2) |
where P is a N × M matrix containing a basis of M orthonormal polynomial functions that takes a potential drift into account. The highest order of the polynomials is M − 1 and l is the M × 1 vector of the drift coefficients. We took M = 3 in our implementation to model 1st and 2nd order drift commonly observed in fMRI times series.
In principle, the HRF response function can be resolved at a finer temporal resolution than the one given by the TR (Dale 1999). We follow a strategy similar to the one proposed by Ciuciu et al. (2003) where the BOLD data and the trial sequence are put on a finer grid and the true onsets of the trials are approximated to the closest neighbors in this finer grid. This approach allows one to model the fMRI time series when the onsets of the stimuli are not synchronized with the acquisition times without oversampling the data.
HRF estimation methods
Least Squares
The least square solution of (2) is obtained by solving
| (3) |
and it is given by
where
where J = (I − PPT). The last equality results from orthonormality of P in our case. The resulting X⊥ amounts to removing the drift from the stimulus convolution matrix (Liu, et al. 2001).
Bayesian method
The Bayesian approach with temporal priors proposed by Marrelec et al. (2003; 2001) makes two assumptions on the unknown HRF. First, it begins and ends at zero, which is accomplished by setting the first and last sample values of the HRF to 0 (Goutte, et al. 2000). Second, the HRF is smooth, which is achieved by setting a Gaussian prior for the norm of the second derivative of the HRF. For full technical details see the references included above. Here we briefly present the key expressions that we used in our computations. In order to estimate the HRF posterior pdf(p(h | y)) Marrelec et al used the approximation
| (4) |
and they proved to be Student-t distributed. In (4) h, y, λ and are the HRF, the fMRI data, the hyper-parameter and its estimate respectively. As the HRF estimate they proposed the expected value of given by
| (5) |
where Q = LTL, L is a (Ns − 2)×(Ns − 2) matrix representing the discrete second derivative operator. The application of the boundary conditions implies removing the first and last column of matrices X and X⊥ being their new dimension N × (Ns − 2). This will be true for the three methods compared in this work. For the sake of simplicity we keep the same notation. The regularization parameter λ establishes a tradeoff between fidelity to the data and the smoothness constraint. A greater value of the regularization parameter will produce smoother HRF estimators in Eq.(5). In the particular case λ = 0 the method reduces to the LS method. The posterior pdf of the hyper-parameter λ was deduced to be
| (6) |
where F = N − Ns. The MAP estimate ( = arg max p(λ|y)) based on (6) was proposed as the choice of the regularization parameter. We use the MATLAB optimization toolbox to find providing as initial value λ0 = 1.
Tikhonov regularization
The Tikhonov solution of (2) is obtained by solving the following optimization problem:
| (7), |
instead of the problem defined by Eq.(3). The second term imposes smoothness on the estimated HRF while the first expresses its fidelity to the data. The regularization parameter has a similar interpretation as for the Bayesian method. We used as L the discrete second derivative and assumed h1=hNs=0 (Marrelec, et al. 2003). The HRF estimator we derived from Eq.(7) is (see Appendix A)
| (8) |
Note that Eq.(8) and Eq.(5) are the same but we select the regularization parameter using GCV (see appendix C), which is a very popular technique in the inverse problems and ridge regression literature (Golub, et al. 1979; Wahba 1990). In our implementation we used a MATLAB package for regularization available publicly at http://www2.imm.dtu.dk/∼pch/Regutools/regutools.html) (Hansen 1994). For more details about our implementation see the appendixes.
HRF parameters estimation
After estimating the HRF using the methods described above we used the result to compute the TTP, HR and W to compare the different methods for HRF estimation. For an analysis of the physiological meaning of these parameters and potential problems in their interpretation such as confusability we refer the reader to Lindquist and Wager (2007). We computed the HR and TTP as:
where dt is the time resolution of the HRF estimation. For computing W we followed a three step procedure similar to the one proposed by Lindquist and Wager (2007). The first step is to find the earliest time point tu such that tu > TTP and h(tu) < 0.5HR, i.e., the first point after the peak that lies below half maximum. Second, find the latest time point tl such that tl < TTP and h(tt) < 0.5HR, i.e., the last point before the peak that lies below half maximum. As both tu and tl take values below 0.5HR, the distance d1 = tu - tl overestimates the width. Similarly, both tu-1 and tl+1 take values above 0.5HR, so the distance d2 = tu-1 - tl+1 underestimates the width. We then estimated W using the average between these two distances(d1,d2) to perform the comparisons between the HRF estimation techniques.
Measures of performance
The comparative results presented below are based on the relative errors for TTP, HR, W and root mean square error (RMS):
| (9) |
| (10) |
| (11) |
| (12) |
The measures of the relative error were computed for the most efficient design (Dale 1999) generated using a random walk of 1000 iterations. They were expressed in percentages and were averaged across 200 realizations of the noise. In order to make the e(RMS) comparison fair we set h1=hNs=0 for the LS method by removing the first and last columns of the matrix X. The efficiency when optimizing the designs was computed according to Dale (1999) and taking into account the drift (Liu 2001)
| (13) |
we set σ = 1 and V = I in all simulations.
Simulated Data
Generation of event sequences
Single event sequences were generated from three commonly used probabilistic distributions: geometric, uniform and exponential. We always constrained the minimum ITI (ITImin) to be one second. A geometric distribution of the ITI was produced by inserting the null events in the sequence with the same probability (p = 0.5) as the real event (Burock, et al. 1998). The exponential and uniform distributed intervals were based on the corresponding MATLAB functions. In the case of the uniform distribution, for a desired mean ITI (ITImean), we generated interval values between [ITImean −8,ITImean +8], which were truncated for short ITImean values due to the constraint on ITImin. For the exponential distribution in order to guarantee simultaneously the required ITImean and a constraint on ITImin, we choose the parameter of the distribution as ITImean -ITImin and then added ITImin to the generated random values. We also generated sequences with fixed ITI.
HRF test function
In our simulations we used the difference between two gamma densities functions (Friston, et al. 1998; Glover 1999; Worsley, et al. 2002)
where a1 = 6, a2 = 12, b1 = b2 = 0.9, c = 0.35, HR = 0.3. In this case the time to peak was 5.4 s, the amplitude was HR and the W was 5.2 s.
The fMRI signal was simulated by putting together the sequence of events at a finer temporal grid. The events onsets were approximated to the nearest point in the grid and then convolved with the test function h(t). The resulting signal was undersampled to TR and Gaussian white noise with a given SNR ( ) or with a fixed standard deviation was added to the data together with a quadratic drift. The durations of the experiment and the HRF were set to 310 s and 20 s respectively.
Simulations
As explained above the measures of performance were computed for designs that have been optimized according to efficiency and using a random walk. This allowed for a fairer comparison of the least squares method to the regularized techniques since optimizing the design will improve the performance of the former. All simulations were repeated for the three different types of random designs that we implemented (geometric, exponential and uniform), but the results will be presented only for the exponential sequences (with the exception of simulation 3) since the results were similar for the other two types of sequences.
Simulation 1
As described above it is possible in principle to estimate the HRF shape from the model described in Eq. (2) with a temporal resolution finer than the TR of the given fMRI time series. We designed this simulation to assess the effect of increasing the temporal resolution of the HRF estimation across TRs and SNRs (between -2 and 8 db). The ITI were generated with ITImean = 5 s, ITImin = 1 s and TR =1 and 2 s respectively. No quadratic drift was added in these simulations to allow a more clear assessment of the influence of the temporal grid resolution.
Simulation 2
In fMRI data analysis it is generally accepted that there is a need to account for the noise autocorrelation (colored noise) present in the data to increase the estimation efficiency (Worsley, et al. 2002). However, Marrelec et al. (2003) reported their regularized solution to be robust to the structure of the noise and Birn et al. (2002) concluded using a FIR model with simulated white noise and real fMRI resting data that the HRF estimation accuracy is unaffected by colored noise. To test these assertions, we designed the following simulations. One event random designs with TR = 1 s, temporal resolution equal to the TR, and different ITImean (3, 5, 10 and 20 s) were generated. We computed our performance measures for three different types of noise: white (WN), autoregressive order 1 (AR(1)), and autoregressive order 4 (AR(4)). For the AR(1) noise the coefficient was set at 0.3 and for the AR(4) noise coefficients were set at
which are the same values as in Marrelec et al. (2003). The signal to noise ratio was varied between -2 and 8 db.
Simulation 3
In these simulations we compared the performance of the three methods across different experimental designs (exponential, geometric, uniform and fixed-ITI) and ITImean values. The parameters were set to: TR = 2 s, the ITImin = 1 s and the temporal resolution was TR/2. Gaussian white noise with standard deviation 0.2 was added. In these simulations we computed the measures of performance across the 5% most efficient designs in order to more clearly assess the influence of the random design on the HRF estimation.
Simulation 4
These simulations were designed to compare the performance of the two regularization techniques in terms of the regularization parameter selection and variability of the estimates. For different ITImean values (3, 7, 10 and 15 s), we kept track of the generated regularization parameters by both methods for two hundred realizations of the noise. The mean TTP, HR and W values together with their 2.5% lower and upper tails were computed and displayed. Three different levels of white noise (5, 3 and 0 db) were explored. Other parameters in this simulation were TR = 2 s and temporal resolution TR/4.
Real Data
Stimulus Presentation
A healthy volunteer (author RC) provided written consent for MRI scanning. The subject was instructed to maintain fixation on a gray cross in the center of a projection screen and to concentrate on the visual stimulus, a black and white checkerboard (250ms duration) that encompassed ∼3° of visual space displayed using MR-compatible goggles (Resonance Technology, www.mrivideo.com). The subject was instructed to respond as quickly and as accurately as possible to a single flash of the checkerboard using the right index finger on a keypad. The single event-related paradigm was a geometric design optimized in terms of efficiency among 10000 generated at random. It consisted of 78 events totaling 330.8 seconds. The ITImin was 1.7 seconds, and there were null events built into the paradigm (p = 0.5) (Burock, et al. 1998).
Image Acquisition
The experiment was conducted on a 1.5-T GE Echo-speed Horizon LX imaging unit with a birdcage head coil (GE Medical Systems, Milwaukee, WI). Functional imaging was performed in the axial plane using multi-section gradient echo-planar imaging with a field of view of 24cm (frequency) × 15 cm (phase) and an acquisition matrix of 64 × 40 (28 sections, 5-mm thickness, no skip, 2100/40 [TR/TE]). A high resolution structural image was obtained using a 3D spoiled gradient-echo sequence with matrix, 256×256; field of view, 24cm; section thickness, 3mm with no gap between sections; number of sections, 128; and in-plane resolution, 0.94 mm.
Image Processing
Images were motion corrected within SPM99, normalized to Montreal Neurological Institute space using image header information (Maldjian, et al. 1997) combined with the SPM99 normalization, and resampled to 4×4×5 mm using sinc interpolation. Statistical parametric maps were generated using SPM99 from the Wellcome Department of Cognitive Neurology, London, England, and implemented in Matlab (The Mathworks Inc., Sherborn, MA) with an IDL (Research Systems Inc., Boulder, CO) interface. The data sets were smoothed using an 8×8×10 mm full-width-half-maximum Gaussian kernel. The data was high-pass filtered, detrended and globally normalized using the corresponding options in the SPM estimation module. Regional activity was detected using SPM by fitting a regression model based on the stimulus time series convolved with the canonical HRF and the first derivative. Significantly activated regions were identified using the random field theory functions for family wise error rate control present in SPM (cluster size test p < 0.05 corrected). The significantly activated region of the visual cortex containing 371 voxels was selected to carry out the HRF estimation. The SPM pre-processed data (without high pass filtering and global normalization) was fed to a set of MATLAB programs with our implementation of the different HRF estimation techniques. The detrending of the time series was carried out as part of the estimation process as shown in Eq. (2) by including the polynomial term.
Results and Discussion
Effect of the HRF temporal resolution (Simulation 1)
Figure 1 depicts the results up to a time resolution of TR/4. The LS method quickly becomes unstable when a finer temporal grid is used and the quality of the extracted HRF shape is poor, as can be seen from the e(RMS) values at all SNRs. The unstable behavior is even worse for designs where acquisition times and stimulus onsets are synchronized. Both regularization based methods often provide improvements in accuracy as reflected by e(TTP), e(W) and e(RMS) over the LS when using finer temporal grids. Their performance is similar, although the Bayesian method is slightly better in terms of accuracy when estimating the TTP and W and slightly worse when estimating HR. The e(RMS) is a global measure that fails to reflect gains in accuracy when estimating the HRF characteristics (TTP, HR and W). For example, in Figure 1 second row (Tik-GCV) the panel on the right shows very little change in e(RMS) when going from one resolution to the next while at the same time greater changes in accuracy for the TTP and W estimates are seen. This reflects the fact that the main lobe of the HRF is better reconstructed (local improvement) when using finer temporal resolution. Tikhonov-like solutions show oscillations due to suppression of higher frequencies that can be usually observed, in the HRF estimation case, after the main lobe of the HRF. These oscillations affect the e(RMS) measure even though the main lobe (and also TTP, HR and W) is more accurately recovered.
Figure 1.
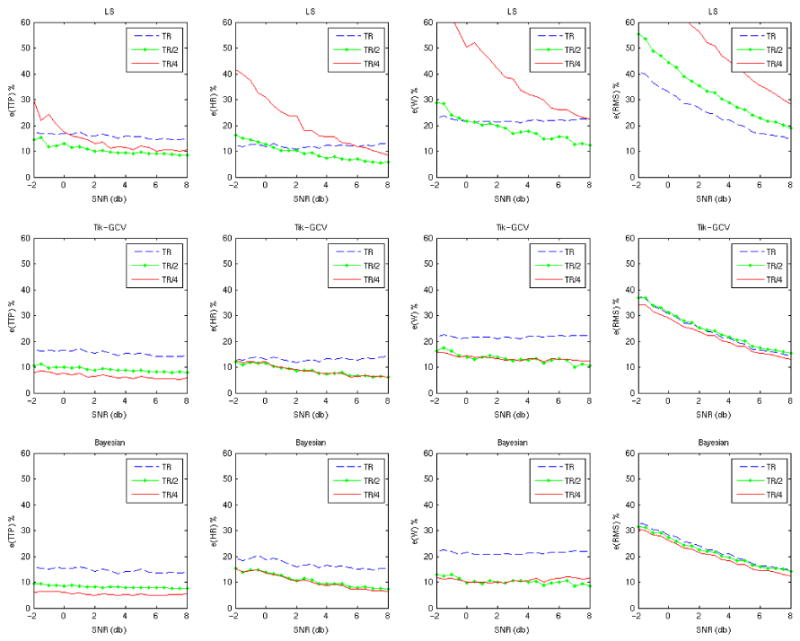
Measures of estimation error for the different parameters (columns) are presented for each method (rows) across temporal resolutions (colored lines). (TR = 2 s, ITImean = 5 s and ITImin = 1 s)
The same simulation was performed with TR = 1 s (not shown). When comparing the results we conclude that in general the longer the TR, the greater the obtained gains in terms of accuracy from the finer time grids when using the regularized methods. The TTP and W benefit the most in terms of accuracy as a function of decreasing temporal grid size.
Effect of the noise autocorrelation (Simulation 2)
The results of these simulations are shown in Figures 2 and 3. In Figure 2 where the ITImean was 3 s, all three methods are relatively robust to the noise autocorrelation according to all measures and for a wide range of SNRs. However, Figure 3 demonstrates that with increasing ITImean (10 s) there is a clear departure of the estimates made by adding AR(4) noise, compared to those made by adding white noise alone. For higher values (15 and 20 s) the departure of AR(1) and AR(4) is even greater (not shown). Very similar results were obtained for all 3 types of random designs (not shown).
Figure 2.
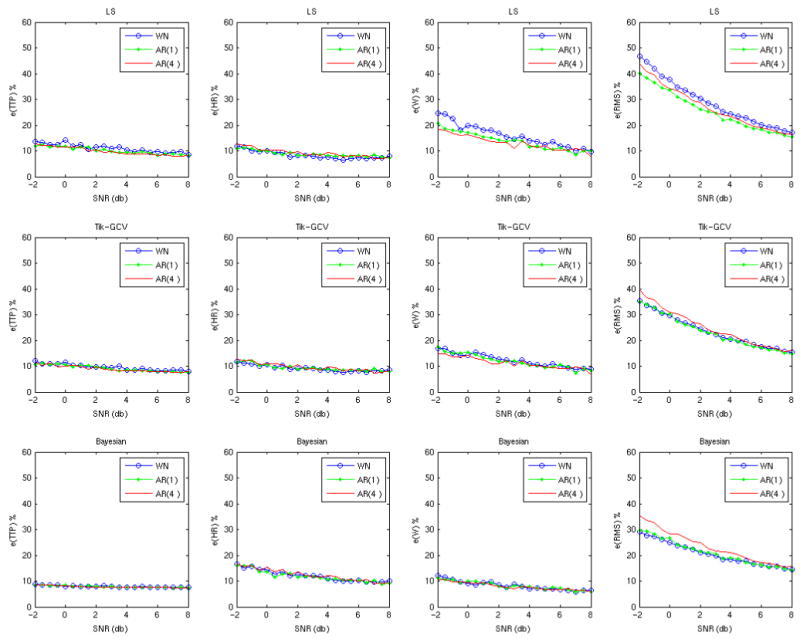
The estimation error of the three methods (rows) when noise with different structure (colored lines) is added to the data with a short ITI. The ITIs were generated using an exponential distribution with ITImean = 3 s, ITImin = 1 s, TR = 1 s and the grid size equal to TR. In this case with a relatively short ITI the estimates are quite robust to the degree of noise autocorrelation.
Figure 3.
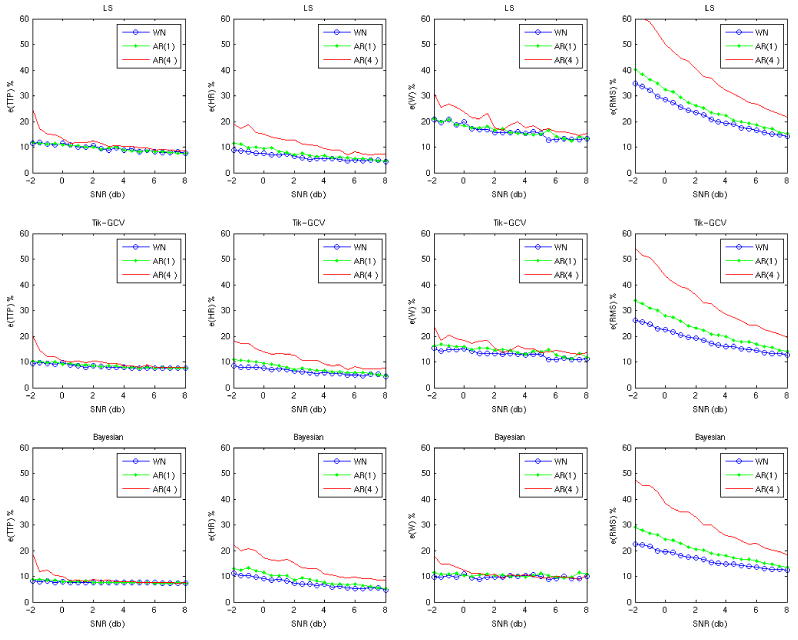
The performance of the three methods (rows) when noise with different structure (colored lines) is added to the data with a long ITI. The ITIs were generated using an exponential distribution with ITImean = 10 seconds, ITImin = 1 s, TR = 1 s and the grid size equal to TR. The long ITImean increases the impact of the noise autocorrelation on the HRF estimates.
Our simulations show that, in general, none of the three methods are robust to the addition of colored noise. A relative robustness is observed only for low values of the ITImean. When the ITImean of the random design is shorter (3 s) its total power is not only greater but also more evenly distributed across frequencies. This implies that increasing the ITImean increases the overlap of the signal with the colored noise (low frequencies) in the frequency domain, making it more likely that the estimation results will be adversely affected by the addition of colored noise.
In the results reported by Marrelec et al. (2003) concerning the robustness of their regularized estimator, the conclusions were based on one randomly generated design most likely with a short ITImean. On the other hand, Birn et al. (2002) based their conclusions about HRF estimability on 200 time series that were taken from a resting state (null) fMRI data set and the degree of autocorrelation was not clear. Woolrich et al.(2001) have reported, based on 6 null fMRI data sets, that for around 50 % of the voxels, the time series show no autocorrelation especially in white matter. This may explain Birn's results but this has to be corroborated.
Effect of the experimental design (Simulation 3)
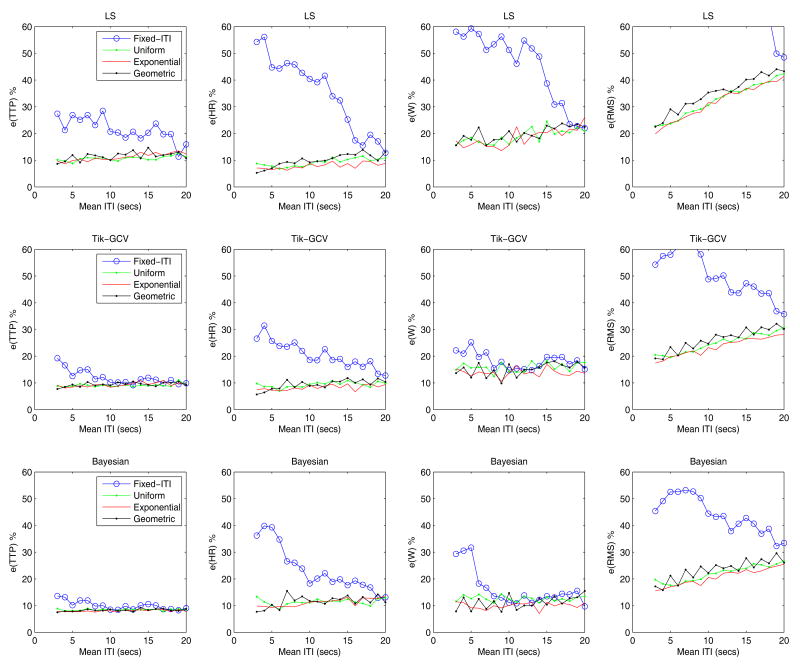
Figure 4 shows that in general, the LS method (first row) does poorly in terms of all measures when a fixed ITI design is used. In addition, it does not perform well in terms of e(RMS) and W for some ITImean values (4, 8, 12…) when the geometric design is employed. In this case, the event onsets are fully synchronized with the acquisition times and the use of a finer temporal grid only worsens the conditioning of the design matrix. With the exception of this particular case, the performance of the LS method is very similar for the three types of random designs we implemented across the whole range of ITImean values.
Figure 4.
The performance of the three methods (rows) is computed across ITImean values and different experimental designs (colored lines). TR = 2 s, temporal grid size TR/2 and Gaussian white noise with std = 0.2 was added.
The two regularization methods often produced better HRF estimates for all experimental designs. Again a very similar performance is observed across the whole range of ITImean values for the three probabilistic distribution of the ITI. Despite the improvements in accuracy produced by the fixed ITI design after regularization, it remains the worst by a large margin.
Comparison of regularization based methods (Simulation 4)
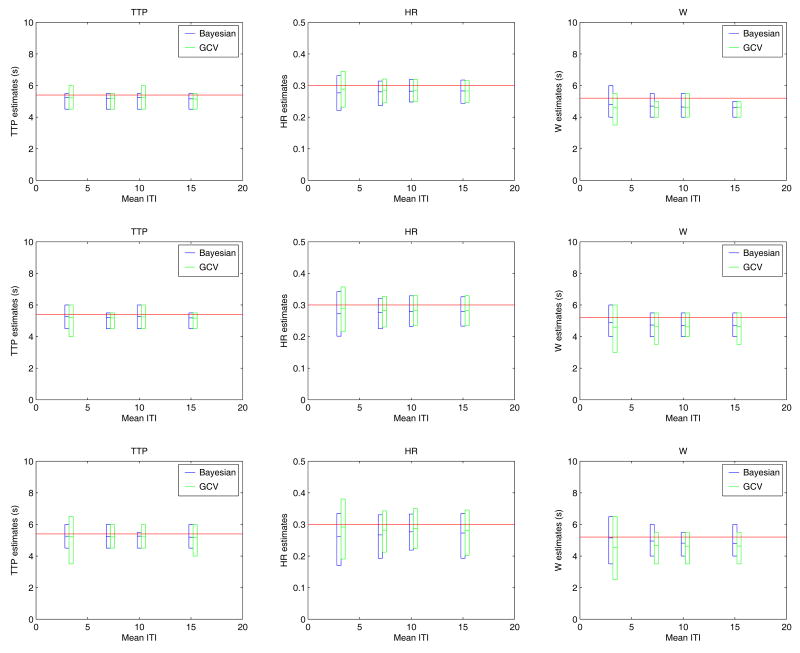
Figure 5 shows the results of comparing the two regularization methods in terms of accuracy and variability of the TTP, HR and W estimates. Each row corresponds to noise levels of 5, 3 and 0 db respectively while each column illustrates the results for a different parameter. The bars represent the mean values and the 2.5% low and upper tails of the estimates.
Figure 5.
The comparative performance of both regularization techniques in terms of accuracy and variability is illustrated for TR = 2 s, grid size TR/4 and 4 different ITImean (3, 7, 10 and 15 s) and exponential sequences. The bars represent the mean value and the 2.5 % lower and upper tails of the estimates. The horizontal lines stand for the real parameters values. The upper, middle and bottom rows correspond to noise levels of 5, 3 and 0 db respectively.
The Bayesian approach often shows less variability than GCV and similar bias when estimating TTP and W. However, when estimating HR the variability is similar but the estimates are slightly more biased than those produced by GCV. These results are fully compatible with the results depicted in Figure 1 for TR/4 and are representative of all simulation scenarios that we have explored.
As expected, the variability of both methods increases with the noise level. In addition, we also observed an increase in the variability of the estimates as ITImean decreased for the same noise level, which could be explained by the greater approximation error incurred when locking events onset times to the employed temporal grid. The greater the number of events, the greater the accumulated approximation error will be.
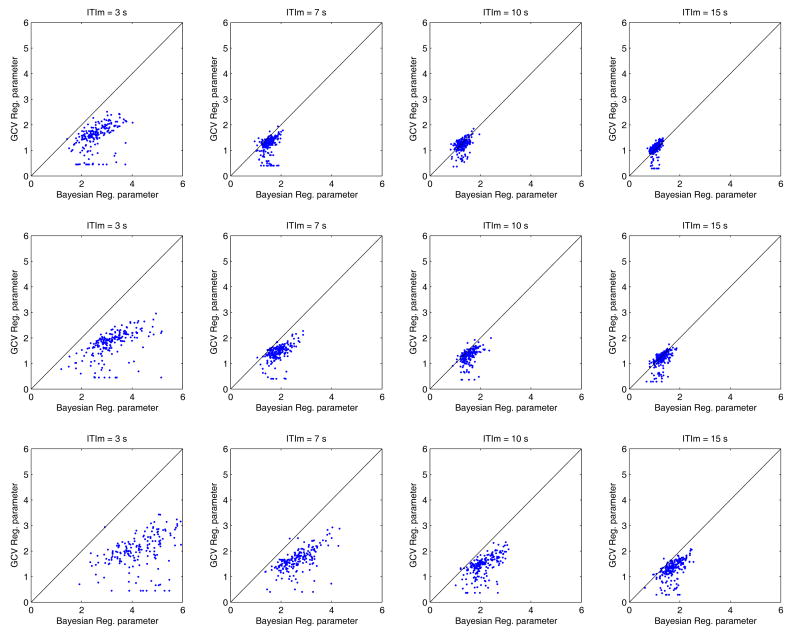
Figure 6 depicts two dimensional plots of the regularization parameters generated by both methods (Bayesian x-axis and GCV y-axis) when performing the simulations reported in Figure 5. Again each row corresponds to a different noise level but now each column represents a different ITImean. The Bayesian approach tends to produce greater regularization parameters with smoother estimators than those produced by Tik-GCV. This is more apparent with a lower SNR and a short ITImean (Figure 6 left bottom corner subplot). As a result, the HR is under-estimated using the Bayesian method, but the TTP and W are more accurately estimated.
Figure 6.
A 2D plot of the regularization parameters generated by both methods (Bayesian x-axis and GCV y-axis) corresponding to the simulation illustrated in Figure 5. The upper, middle and bottom rows correspond to noise levels of 5, 3 and 0 db respectively and each column to a different ITImean. In each plot the line x=y has been included.
Real data results
The real data were collected as described above to illustrate the relative performance of the three methods in a simple experimental setting. First, using SPM99, a region of the visual cortex containing 371 voxels was found to be significantly activated (p < 0.05 cluster test corrected for multiple comparisons) by the single flash event (Figure 7 upper row). The results of applying the least squares, Tik-GCV and the Bayesian estimation methods using a temporal grid size TR/4 are shown in Figure 7. The bottom row shows the voxel-wise estimated HRFs with the average HRF computed across all voxels in the region shown as black thick lines. The LS method becomes highly unstable for the TR/4 temporal grid while the regularized techniques manage to produce meaningful and similar results.
Figure 7.
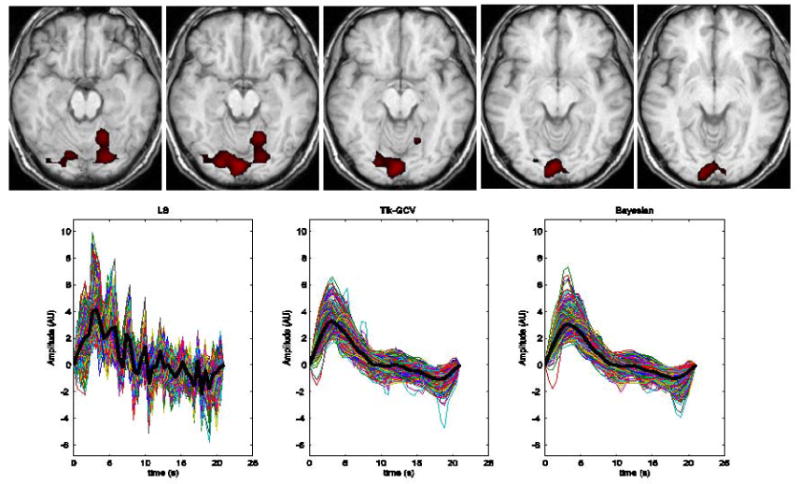
In the upper row, slices of a significantly activated area (p < 0.05 cluster corrected) of the visual cortex are shown. Estimates of the HRF were based on all voxels within this region of significant activation as determined using SPM99. The voxel wise HRF estimate produced by the 3 methods are displayed in the bottom row with the corresponding average HRF across the activated area shown as black thick lines. The LS method becomes very unstable while the regularization based methods are able to produce meaningful results. The estimated values for (TTP, HR, W) produced by LS, Tik-GCV and the Bayesian methods are (3.15 s, 4.16, 2.1 s), (3.15 s, 3.27, 4.72 s) and (3.15 s, 3.07, 4.73 s) respectively.
Conclusions
In this work we have studied improvements in HRF estimation produced by the use of temporal regularization with respect to the more traditional and widely used least squares approach. The comparison was made in terms of the accuracy achieved when HRF features such as the time to peak, response amplitude and width were computed from the estimated HRFs. The results show that regularization based methods often outperform the least squares approach, especially when SNR is low and oversampling is employed. A topic of particular concern was the impact of the HRF temporal resolution on the accuracy of TTP, HR and W estimates. Our simulations show that the use of discretization resolutions finer than the TR produces greater improvements for longer TRs (2 s), a situation very common in fMRI studies allowing most of the brain to be imaged. Decreasing the grid size to less than TR/4 produces small gains in terms of accuracy although TTP and W estimates still showed some improvements when Tik-GCV is used. We have also shown that by refining the time resolution of the estimation, valuable information about the HRF time course can be extracted without resorting to nonlinear optimization and assumption of a fixed HRF shape as has been done before (Miezin, et al. 2000).
Another issue of interest was the robustness of all three estimation methods to the color of the noise. Previous reports suggest that HRF estimation techniques that do not assume a fixed shape of the HRF are quite robust to the presence of auto-correlated noise. However, our analysis suggests that the three methods we studied were relatively robust to the color of the noise only with short ITImean values. At longer ITImean, the signal's total power is lesser and with more content in the lower frequencies, which makes the estimates more likely to be affected by the fMRI noise autocorrelation. We conclude that the noise autocorrelation structure should definitely be taken into account to reduce the variability of the estimates when using these techniques. To our knowledge, these observations highlight for the first time the influence of autocorrelations on the estimated shape of the HRF; the bulk of the literature focuses on the influence of autocorrelation on statistical detection and inference (Bullmore, et al. 2001; Smith, et al. 2007; Worsley, et al. 2002).
We also evaluated the influence of the stimulus sequence on the estimates produced by each of the three estimation methods. We found that the performance of each the three methods individually are similar for uniform, exponential and geometric designs (with the exception of LS when combined with synchronized geometric sequences). Regularization produces more accurate HRF estimates across the whole range of ITImean. For synchronized geometric sequences the regularization produces a significant improvement in estimation when using a temporal grid finer than the TR. Despite the improvement in performance due to regularization, the fixed-ITI design produces a less accurate HRF estimates overall.
Though the goal of this work was not to pursue a detailed comparison of Bayesian and GCV regularization techniques, we noted some differences in our simulations. The Bayesian approach tends to produce smoother HRF estimates than GCV. The results are similar in general up to a temporal resolution of TR/4, but the former is consistently more accurate and shows less variability for determining the time to peak and the width of the HRF while the latter is slightly more accurate for estimating the amplitude of the response. At finer than TR/4 temporal grids, Tik-GCV behavior was more robust. A possible shortcoming in this comparison is that the designs were optimized using an efficiency metric which is frequentist in nature (expected error over many experiments) while the use of a Bayesian measure could in theory improve the performance of the Marrelec et al. (2001,2003) method at finer temporal resolutions. We do not explore this issue here; however, despite this possible shortcoming in this comparison we find that the Bayesian method does quite well. In terms of computational cost all simulations and tests with real data made so far show that Tik-GCV is much faster than the Bayesian approach. For a more conclusive evaluation of the relative performance of these two techniques, additional research is needed.
Finally, it is important to remark that all of our conclusions are based on the assumption of linearity and time invariance of the fMRI BOLD signal. While significant non-linearities are sometimes observed in real data, the assumption of linearity is reasonable in many experimental situations. The conclusions made about the impact of the color of the noise on HRF estimation (simulation 2) were based on the assumption of autoregressive models of the noise that, although a common model used in fMRI data analysis, is not the only option.
Acknowledgments
This work was supported by the Human Brain Project and NIBIB through grant number EB004673, and by NS042568, and EB003880. The authors would like to thank Kathy Pearson for her programming support during this project. We also thank the anonymous reviewers for their helpful comments that significantly strengthened this work.
Appendix A
The Tikhonov functional defined by Eq.(7) can be rewritten as
| (14) |
Where O is a Ns × sdM matrix composed of zeros, Xext = [X P] and Lext = [L O].
The solution of the last equation is
| (15) |
Now we replace in Eq. (15) Xext = [X P] and Lext = [L O]. This result is
In the last equality the fact that P is orthogonal (PTP = I) was used. Now Eq.(15) becomes
| (16) |
To invert the block matrix in Eq.(16) we used properties for inversion of block matrices (Behrens and Scharf 1994) (see also http://ccrma.stanford.edu/∼jos/lattice/Block_matrix_decompositions.html)
We obtain
| (17) |
Then we have
| (18) |
This is the Tik-GCV HRF estimator given in Eq.(8) and it is the same as the one proposed by Marrelec et al. (2001, 2003) that we have obtained using a completely different rationale.
In a similar way it can be shown that
| (19) |
We compute the regularization parameter by noting that Eq.(18) is also the solution of the Tikhonov functional
| (20) |
Eq.(20) is transformed to the standard form (see Appendix B) and the regularization parameter is computed using GCV (see Appendix C).
Appendix B
When it comes to dealing with Eq. 20 algorithmically, it is more efficient if it is written in the so called standard form (Hanke and Hansen 1993). This refers to the case where L = I. If L is invertible, an obvious transformation to standard form is given by Lh = h* which leads to the new problem formulation
| (21) |
where X * = X⊥L−1. After solving (21) the solution of the problem given by Eq.(20) is obtained as h = L−1h*. The regularization parameter is computed using the GCV. One important computational advantage is that the evaluation of the GCV function greatly simplifies when the problem is in the standard form.
Appendix C
Generalized cross-validation
We follow the description of the rationale behind GCV provided by (Hanke and Hansen 1993) although the notation is the one used in our paper for consistency, and we assume L = I. The GCV was developed as an improvement over the ordinary cross-validation (OCV), which is based on the philosophy that if an arbitrary element of the data y is left out, then the corresponding solution should predict this observation well.
Let λ be fixed for the moment and assume that we try to estimate one component yi of the data vector y from the remaining N − 1 components in the following way:
We first apply Tikhonov regularization with the chosen λ to the modify system X′h* = y′ which is obtained from X*h* = y by deleting the i-th equation. Let hλ,i denote the resulting approximation.
Then, hλ,i is used to estimate yi as X*hλ,i.
It can be expected that a good choice of λ is one for which the error of the above estimation, averaged with reasonable weights over all possible values of i ∈ {1,…, N}, becomes small. This is the basis for GCV, where the optimal λ is chosen to be the minimizer of the function
| (21) |
where A(λ) = X* (X*TX* + λ2I)−1 X*T. The expression given by Eq.(21) can be simplified by the use of the singular value decomposition or bidiagonalization (Elden 1984). The former (SVD) is the method used by the Hansen regularization toolbox. For more technical details and a rigorous discussion about GCV see (Wahba,1990).
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Aguirre GK, Zarahn E, D'Esposito M. The Variability of Human, BOLD Hemodynamic Responses. Neuroimage. 1998;8(4):360–369. doi: 10.1006/nimg.1998.0369. [DOI] [PubMed] [Google Scholar]
- Behrens RT, Scharf LL. Signal Processing Applications of Oblique Projection Operators. IEEE Trans on signal processing. 1994;42(6):14, 13–1424. [Google Scholar]
- Birn RM, Cox RW, Bandettini PA. Detection versus estimation in event-related fMRI: choosing the optimal stimulus timing. Neuroimage. 2002;15(1):252–64. doi: 10.1006/nimg.2001.0964. [DOI] [PubMed] [Google Scholar]
- Boynton GM, Engel SA, Glover GH, Heeger DJ. Linear systems analysis of functional magnetic resonance imaging in human V1. J Neurosci. 1996;16(13):4207–21. doi: 10.1523/JNEUROSCI.16-13-04207.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E, Long C, Suckling J, Fadili J, Calvert G, Zelaya F, Carpenter TA, Brammer M. Colored noise and computational inference in neurophysiological (fMRI) time series analysis: resampling methods in time and wavelet domains. Hum Brain Mapp. 2001;12(2):61–78. doi: 10.1002/1097-0193(200102)12:2<61::AID-HBM1004>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burock MA, Buckner RL, Woldorff MG, Rosen BR, Dale AM. Randomized event-related experimental designs allow for extremely rapid presentation rates using functional MRI. Neuroreport. 1998;9(16):3735–9. doi: 10.1097/00001756-199811160-00030. [DOI] [PubMed] [Google Scholar]
- Buxton RB, Uludag K, Dubowitz DJ, Liu TT. Modeling the hemodynamic response to brain activation. Neuroimage. 2004;23 1:S220–33. doi: 10.1016/j.neuroimage.2004.07.013. [DOI] [PubMed] [Google Scholar]
- Buxton RB, Wong EC, Frank LR. Dynamics of blood flow and oxygenation changes during brain activation: the balloon model. Magn Reson Med. 1998;39(6):855–64. doi: 10.1002/mrm.1910390602. [DOI] [PubMed] [Google Scholar]
- Ciuciu P, Poline JB, Marrelec G, Idier J, Pallier C, Benali H. Unsupervised robust nonparametric estimation of the hemodynamic response function for any fMRI experiment. IEEE Trans Med Imaging. 2003;22(10):1235–51. doi: 10.1109/TMI.2003.817759. [DOI] [PubMed] [Google Scholar]
- Dale A. Optimal Experimental Design for Event-Related fMRI. Human Brain Mapping. 1999;8:109–114. doi: 10.1002/(SICI)1097-0193(1999)8:2/3<109::AID-HBM7>3.0.CO;2-W. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale A, Buckner RL. Selected averaging of rapidly presented individual trials using fMRI. Human Brain Mapping. 1997;5:329–340. doi: 10.1002/(SICI)1097-0193(1997)5:5<329::AID-HBM1>3.0.CO;2-5. [DOI] [PubMed] [Google Scholar]
- Elden L. A note on the computation of the generalized cross-validation function for ill-conditioned least squares problems. BIT. 1984;24:467–472. [Google Scholar]
- Friston KJ, Holmes AP, Worsley KJ, Poline JB, Frith C, Frackowiak RSJ. Statistical Paramteric Maps in functional imaging: A General Linear Approach. Human Brain Mapping. 1995;2:189–202. [Google Scholar]
- Friston KJ, Jezzard P, Turner R. Analysis of functional MRI time series. Human Brain Mapping. 1994;1:153–171. [Google Scholar]
- Friston KJ, Josephs O, Rees G, Turner R. Nonlinear event-related responses in fMRI. Magn Reson Med. 1998;39(1):41–52. doi: 10.1002/mrm.1910390109. [DOI] [PubMed] [Google Scholar]
- Friston KJ, Penny W, Phillips C, Kiebel S, Hinton G, Ashburner J. Classical and Bayesian inference in neuroimaging: theory. Neuroimage. 2002;16(2):465–83. doi: 10.1006/nimg.2002.1090. [DOI] [PubMed] [Google Scholar]
- Glover GH. Deconvolution of Impulse Response in Event-Related BOLD fMRI. Neuroimage. 1999;9:416–429. doi: 10.1006/nimg.1998.0419. [DOI] [PubMed] [Google Scholar]
- Golub GH, Heath M, Wahba G. Generalized Cross-Validation as a Method for Choosing a Good Ridge Parameter. Technometrics. 1979;21(2):215–223. [Google Scholar]
- Goutte C, Nielsen FA, Hansen LK. Modeling the Haemodynamic Response in fMRI Using Smooth FIR Filters. IEEE Transactions on Medical Imaging. 2000;19(12):1188–1201. doi: 10.1109/42.897811. [DOI] [PubMed] [Google Scholar]
- Hagberg GE, Zito G, Patria F, Sanes JN. Improved detection of event-related functional MRI signals using probability functions. Neuroimage. 2001;14(5):1193–205. doi: 10.1006/nimg.2001.0880. [DOI] [PubMed] [Google Scholar]
- Handwerker DA, Ollinger JM, D'Esposito M. Variation of BOLD hemodynamic responses across subjects and brain regions and their effects on statistical analyses. Neuroimage. 2004;21(4):1639–51. doi: 10.1016/j.neuroimage.2003.11.029. [DOI] [PubMed] [Google Scholar]
- Hanke M, Hansen C. Regularization methods for large scale problems. Surveys on Mathematics for Industry. 1993;3:253–315. [Google Scholar]
- Hansen PC. Regularization Tools: A Matlab package for analysis and solution of discrete ill-posed problems. Numerical Algorithms. 1994;6:1–35. [Google Scholar]
- Lange N, Strother SC, Anderson JR, Nielsen FA, Holmes AP, Kolenda T, Savoy R, Hansen LK. Plurality and resemblance in fMRI data analysis. Neuroimage. 1999;10(3 Pt 1):282–303. doi: 10.1006/nimg.1999.0472. [DOI] [PubMed] [Google Scholar]
- Lindquist MA, Wager TD. Validity and power in hemodynamic response modeling: A comparison study and a new approach. Human Brain Mapping. 2007;28(8):764–784. doi: 10.1002/hbm.20310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu TT, Frank LR, Wong EC, Buxton RB. Detection Power, Estimation Efficiency and Predictability in Event-Related fMRI. Neuroimage. 2001;13:759–773. doi: 10.1006/nimg.2000.0728. [DOI] [PubMed] [Google Scholar]
- Logothetis NK, Pfeuffer J. On the nature of the BOLD fMRI contrast mechanism. Magn Reson Med. 2004;22:1517–1531. doi: 10.1016/j.mri.2004.10.018. [DOI] [PubMed] [Google Scholar]
- Lu Y, Bagshaw AP, Grova C, Kobayashi E, Dubeau F, Gotman J. Using voxel-specific hemodynamic response function in EEG-fMRI data analysis. Neuroimage. 2006;32:238–247. doi: 10.1016/j.neuroimage.2005.11.040. [DOI] [PubMed] [Google Scholar]
- Lu Y, Grova C, Kobayashi E, Dubeau F, Gotman J. Using voxel-specific hemodynamic response function in EEG-fMRI data analysis: An estimation and detection model. Neuroimage. 2007;34(1):195–203. doi: 10.1016/j.neuroimage.2006.08.023. [DOI] [PubMed] [Google Scholar]
- Maldjian JA, Schulder M, Liu WC, Mun IK, Hirschorn D, Murthy R, Carmel P, Kalnin A. Intraoperative functional MRI using a real-time neurosurgical navigation system. J Comput Assist Tomogr. 1997;21(6):910–2. doi: 10.1097/00004728-199711000-00013. [DOI] [PubMed] [Google Scholar]
- Marrelec G, Benali H, Ciuciu P, Pelegrini-Issac M, Poline JB. Robust Estimation of the Hemodynamic Response Function in Event-Related BOLD fMRI Using Basic Physiological Information. Human Brain Mapping. 2003;19:1–17. doi: 10.1002/hbm.10100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marrelec G, Benali H, Ciuciu P, Poline JB. In: Bayesian estimation of the hemodynamic of the hemodynamic response function in functional MRI. R F, editor. Melville: 2001. pp. 229–247. [Google Scholar]
- Menon RS, Luknowsky DC, Gati JS. Mental chronometry using latency-resolved functional MRI. Proc Natl Acad Sci U S A. 1998;95(18):10902–7. doi: 10.1073/pnas.95.18.10902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miezin FM, Maccotta L, Ollinger JM, Petersen SE, Buckner RL. Characterizing the hemodynamic response: effects of presentation rate, sampling procedure, and the possibility of ordering brain activity based on relative timing. Neuroimage. 2000;11(6 Pt 1):735–59. doi: 10.1006/nimg.2000.0568. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proc Natl Acad Sci U S A. 1990;87(24):9868–72. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ollinger JM, Corbetta M, Shulman GL. Separating processes within a trial in event-related functional MRI. Neuroimage. 2001a;13(1):218–29. doi: 10.1006/nimg.2000.0711. [DOI] [PubMed] [Google Scholar]
- Ollinger JM, Shulman GL, Corbetta M. Separating processes within a trial in event-related functional MRI. Neuroimage. 2001b;13(1):210–7. doi: 10.1006/nimg.2000.0710. [DOI] [PubMed] [Google Scholar]
- Serences JT. A comparison of methods for characterizing the event related BOLD timeseries in rapid fMRI. Neuroimage. 2004;21:1690–1700. doi: 10.1016/j.neuroimage.2003.12.021. [DOI] [PubMed] [Google Scholar]
- Smith AT, Singh KD, Balsters JH. A comment on the severity of the effects of non-white noise in fMRI time-series. Neuroimage. 2007;36(2):282–8. doi: 10.1016/j.neuroimage.2006.09.044. [DOI] [PubMed] [Google Scholar]
- Tikhonov AN, Arsenin VY. Solution of ill-posed problems. Washington DC: W.H. Winston; 1977. [Google Scholar]
- Vakorin VA, Borowsky R, Sarty GE. Characterizing the functional MRI response using Tikhonov regularization. Stat Med. 2007;26(21):3830–44. doi: 10.1002/sim.2981. [DOI] [PubMed] [Google Scholar]
- Wahba G. Spline Models for Observational Data. Philadelphia: SIAM; 1990. [Google Scholar]
- Woolrich MW, Ripley BD, Brady M, Smith SM. Temporal autocorrelation in univariate linear modeling of FMRI data. Neuroimage. 2001;14(6):1370–86. doi: 10.1006/nimg.2001.0931. [DOI] [PubMed] [Google Scholar]
- Worsley KJ, Liao CH, Aston J, Petre V, Duncan GH, Morales F, Evans A. A General Statistical Analysis for fMRI Data. Neuroimage. 2002;15:1–15. doi: 10.1006/nimg.2001.0933. [DOI] [PubMed] [Google Scholar]
- Zhang CM, Jiang Y, Yu T. A comparative study of one-level and two-level semiparametric estimation of hemodynamic response function for fMRI data. Stat Med. 2007;26(21):3845–61. doi: 10.1002/sim.2936. [DOI] [PubMed] [Google Scholar]