Direct observation of fast protein conformational switching

Abstract

Folded proteins can exist in multiple conformational substates. Each substate reflects a local minimum on the free-energy landscape with a distinct structure. By using ultrafast 2D-IR vibrational echo chemical-exchange spectroscopy, conformational switching between two well defined substates of a myoglobin mutant is observed on the ≈50-ps time scale. The conformational dynamics are directly measured through the growth of cross peaks in the 2D-IR spectra of CO bound to the heme active site. The conformational switching involves motion of the distal histidine/E helix that changes the location of the imidazole side group of the histidine. The exchange between substates changes the frequency of the CO, which is detected by the time dependence of the 2D-IR vibrational echo spectrum. These results demonstrate that interconversion between protein conformational substates can occur on very fast time scales. The implications for larger structural changes that occur on much longer time scales are discussed.

A folded protein with a particular structure occupies a minimum on its free-energy landscape (1–3). However, the minimum is frequently a local minimum. Other minima of similar energy can also exist. When a protein occupies any one of these minima, it has a distinct structure. The different structures are substates of the folded protein. Transitions from one minimum to another correspond to dynamical changes in the structure of the protein that take the protein from one substate to another. Under thermal equilibrium conditions, there will be continual conformational switching among substates. In addition to interconversion between substates, proteins undergo continuous structural fluctuations within a particular substate minimum. Such fluctuations within a substate minimum give rise to processes such as small ligand “diffusion” through a protein to an active site (4).

The ability of proteins to undergo conformational switching is central to protein function. When an enzyme binds a substrate, the protein conformation will change (5). On the path of protein folding, a protein will sample many conformations as it progresses toward the native folded structure (6). Proteins can undergo large global conformational changes, which occur on long time scales, milliseconds to seconds. However, these large, slow conformational changes, such as those that occur after substrate binding to an enzyme, involve a vast number of more local elementary conformational steps.

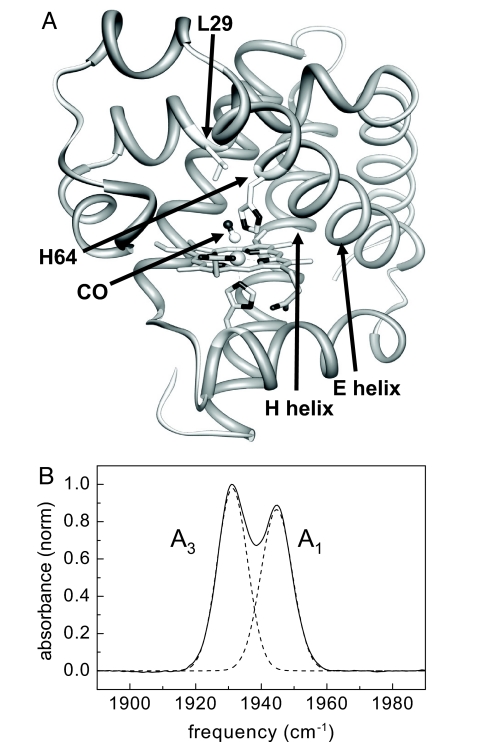
The experimental determination for the time scale of elementary conformational steps is a long-standing problem that has now been addressed successfully by using ultrafast 2D-IR vibrational echo chemical-exchange spectroscopy. The problem of substate switching has been studied extensively for the protein myoglobin (Mb) with the ligand CO bound at the active site (MbCO) (7–9). The Fourier transform IR (FT-IR) spectrum of the heme-ligated CO stretching mode of Mb has three absorption bands, denoted A₀ (1,965 cm⁻¹), A₁ (1,945 cm⁻¹), and A₃ (1,932 cm⁻¹) (10). MbCO interconverts among these three conformational substates under thermal equilibrium. The distal histidine, His-64, has a prominent role in determining the conformational substates of Mb (Fig. 1A). Changes in the configuration of the distal histidine cause its imidazole side group to move relative to the CO (10, 11). When the conformation of the distal histidine results in the imidazole being rotated out of the heme pocket, the interaction of the distal histidine with the ligated CO becomes weak. This out-of-the-pocket configuration gives rise to the A₀ band (9, 12). The distal histidine conformation that places the imidazole in the heme pocket gives rise to two substates, A₁ and A₃, which involve strong interactions of the imidazole side group with the CO ligand. The lower frequency of A₃ compared with A₁ reflects a closer proximity of the imidazole to the CO in A₃ (11, 13, 14). Each A substate exhibits a distinct ligand binding rate (2, 7). Therefore, the three peaks in the FT-IR spectrum of MbCO reflect functionally distinct conformational substates.

Fig. 1.

Structure of CO-bound myoglobin. (A) Crystal structure of MbCO taken from the Protein Data Bank (ID code 1MWC). The distal histidine, His-64; the CO; the location of Leu-29; and the E helix are indicated. (B) FT-IR spectrum of the CO stretch of heme-ligated CO for the myoglobin mutant L29I (solid curve). The spectrum was fitted by two Gaussians (dashed curves), which represent the absorption bands of the A₁ and A₃ substates.

By using flash photolysis measurements, the kinetic rate constant for the A₀ − A₁/A₃ conformational switching, in which the distal histidine swings its imidazole side group out of and into the heme pocket, is estimated to be in the range of ≈1–10 μs (8, 13). These indirect measurements based on ligand binding rate constants have also been applied to the A₁ and A₃ interconversion by using low-temperature flash photolysis studies. The results were extrapolated to ambient temperature and yield <1 ns for switching between A₁ and A₃ (13). Molecular dynamics (MD) simulations have placed the A₁–A₃ switching time on the order of 100–200 ps (14).

It has been difficult to directly measure fast elementary substate interconversion times, including the A₁-A₃ switching. Here, we report a direct measurement of the A₁–A₃ substate switching time under thermal equilibrium conditions by using 2D-IR vibrational echo chemical-exchange spectroscopy. This method has recently proven useful for studying fast dynamical processes in liquids (15–17). The 2D-IR vibrational echo chemical-exchange experiment is akin to a 2D NMR chemical-exchange experiment, except that it can operate on a picosecond time scale, and it directly probes the structural degrees of freedom through the time evolution of the 2D vibrational spectrum. The A₁ and A₃ peaks in the FT-IR spectrum appear as bands on the diagonal of the 2D-IR vibrational echo spectrum. As time increases, cross peaks grow in because of the interconversion between the A₁ and A₃ substates (chemical exchange). Analysis of the time-dependent growth of the chemical-exchange peaks yields the A₁ going to A₃ interconversion time of 47 ps.

Results and Discussion

The FT-IR spectrum of wild-type MbCO shows three discrete CO stretching bands, the A₀, A₁, and A₃ bands (7, 10, 18). The A₁ substate of wild-type MbCO is predominately populated and dominates the absorption spectrum. Because the A₃ absorption peak of wild-type MbCO is relatively small compared with the A₁ peak, we performed the experiments on an Mb mutant, L29I, in which a leucine is replaced with an isoleucine (10). This small change causes the A₁ and A₃ bands in the FT-IR spectrum to be approximately the same size (Fig. 1B). Like wild-type MbCO, the amount of A₀ conformation is small in the L29I mutant (≈5%). Changes at position 29 cause a slight modification of the configuration of the distal histidine because the amino acid residue at position 29 interacts with the imidazole side chain of the distal histidine (Fig. 1A) (10). In the background-subtracted FT-IR spectrum shown in Fig. 1B, the two L29I CO absorption bands are at 1,932 cm⁻¹ and 1,945 cm⁻¹. These bands correspond to the A₃ and A₁ substates, respectively (10). The peak positions for the CO absorption bands of L29I are essentially identical to those of wild-type Mb within the reported significant figures (10).

Experimental details for performing 2D-IR vibrational echoes and chemical-exchange experiments have been presented previously (15, 17, 19, 20). Qualitatively, the experimental method works in the following manner. Three ultrashort IR pulses tuned to the frequency of the A₁ and A₃ vibrational modes are crossed in the sample. The IR excitation pulses, 110 fs and 150 cm⁻¹ FWHM, are produced with a Ti:sapphire regenerative amplifier-pumped optical parametric oscillator. Because the pulses are very short, they have a broad bandwidth that makes it possible to simultaneously excite the vibrational modes of both the A₁ and A₃ substates. The first laser pulse “labels” the initial structures of the species by defining their initial frequency, ω_τ. The second pulse ends the first time period τ and starts clocking the reaction time period T_w during which the labeled species undergo substate switching (chemical exchange) and vibrational relaxation to the ground state. The third pulse ends the population dynamics period of length T_w and begins a third period of length ≤τ, which ends with the emission of the vibrational echo pulse of frequency ω_m. The vibrational echo signal reads out information about the final structures of all labeled species by their frequency ω_m.

There are two types of time periods in the experiment. The times between pulses 1 and 2 and between pulse 3 and the vibrational echo pulse are called coherence periods. During these periods, the vibrations are in coherent superpositions of two vibrational states. Fast vibrational oscillator frequency fluctuations induced by fast structural fluctuations of the protein cause dynamic dephasing, which is one contribution to the line shapes in the conventional 1D absorption spectrum. During the period T_w between pulses 2 and 3, called the population period, a vibration is in a vibrational eigenstate. Slower structural fluctuations of the protein cause the CO frequency to evolve in time. This time evolution of the frequency, termed spectral diffusion, contributes to the 2D line shapes. Other processes during the population period, particularly chemical exchange, also produce changes in the 2D spectrum. Chemical exchange occurs when two species in equilibrium interconvert without changing the overall number of either species. Interconversion back and forth between the A₁ and A₃ substates is a type of chemical exchange. In other contexts, it has been demonstrated that chemical exchange causes new cross peaks to grow in as T_w is increased (15–17, 21–23). The growth of the cross peaks with increasing time is directly related to the chemical-exchange rate (15–17, 21–23). Here, the growth of the cross peaks in the 2D vibrational echo spectrum of L29I with increasing T_w is used to extract the A₁–A₃ substate interconversion rate.

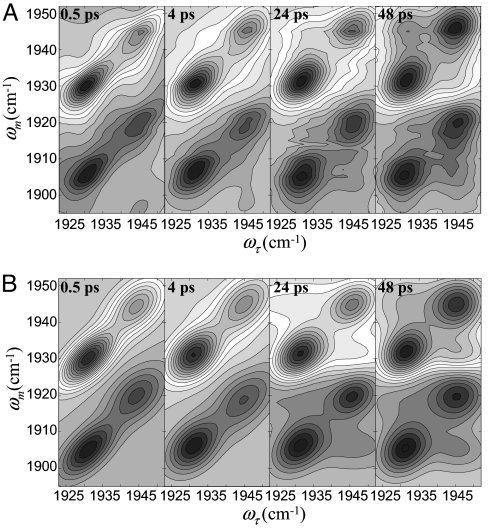
Fig. 2A shows 2D-IR spectra of CO bound to L29I at several T_w values. The bands in the upper half of the spectrum are positive-going and correspond to the 0–1 vibrational transitions. The bands in the lower half of the spectrum are negative-going, which arise from vibrational echo emission at the frequency of the 1–2 vibrational transition. The negative-going bands are shifted along the ω_m axis by the anharmonicity of CO stretching mode (24, 25). The data have been normalized to the largest peak at each T_w. Consider the spectrum for T_w = 0.5 ps. The two bands on the diagonal correspond to the two peaks in the absorption spectrum shown in Fig. 1B. These two bands are centered at (ω_τ, ω_m) = (1,932 cm⁻¹, 1,932 cm⁻¹) and (1,945 cm⁻¹, 1,945 cm⁻¹) corresponding to the A₃ and A₁ substates, respectively. The off-diagonal band centered at (ω_τ, ω_m) = (1,932 cm⁻¹, 1,908 cm⁻¹) and (1,945 cm⁻¹, 1,922 cm⁻¹) are from vibrational echo emission at the 1–2 vibrational transitions of the A₃ and A₁ substates, respectively. At T_w = 0.5 ps, there are no cross peaks in the 0–1 and 1–2 regions because 0.5 ps is short relative to the conformational switching time.

Fig. 2.

2D-IR spectra of CO bound to L29I. (A) 2D-IR spectra of L29I-CO at various times, T_w. Each contour corresponds to a 10% signal change. The bands in the upper half of the spectrum (positive-going) correspond to the 0–1 vibrational transition. The bands in the lower half of the spectrum (negative-going) arise from vibrational echo emission at the 1–2 transition frequency. (B) Calculated 2D-IR spectra of L29I-CO at various times, T_w, using the known input parameters and the substate switching time constant obtained from fitting the data.

In contrast, by T_w = 48 ps (Fig. 2A) enough time has elapsed for conformational switching to occur to a significant extent. The conformational switching is manifested by the growth of cross peaks (17), which are most apparent in the upper left portion of the 0–1 bands and the lower right portion of the 1–2 bands. These cross peaks correspond to the A₃ switching to A₁ and A₁ switching to A₃, respectively. Because the system is in equilibrium, the rate of A₁ converting into A₃ is equal to the rate of A₃ converting into A₁. If the anharmonicity is sufficiently large, so that the positive-going 0–1 bands do not overlap with the negative-going 1–2 bands, then the cross peaks appear symmetrically about the 0–1 diagonal peaks and the corresponding 1–2 peaks (17). Here, the overlap of the positive- and negative-going bands reduces the amplitudes of the other two cross peaks, that is, the 0–1 A₁ to A₃ cross peak at (ω_τ, ω_m) = (1,945 cm⁻¹, 1,932 cm⁻¹) and the 1–2 A₃ to A₁ cross peak at (ω_τ, ω_m) = (1,932 cm⁻¹, 1,920 cm⁻¹).

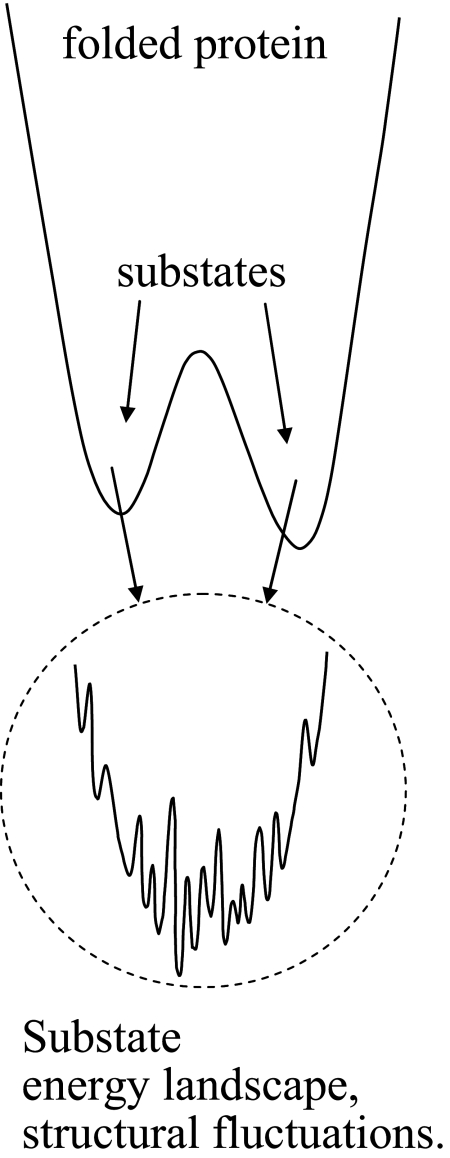
In addition to the growth of the cross peaks in Fig. 2A, the shapes of the bands change with increasing T_w. At short T_w, the 2D line shapes show significant inhomogeneous broadening. Inhomogeneous broadening is evidenced by elongation along the diagonal. As time proceeds, protein structural fluctuations within a given substate structure cause the transition frequency to vary (spectral diffusion) (26–31). The landscape minimum associated with each substate is relatively shallow and has many local minima separated by small barriers (see Fig. 4). Transitions among these minima produce structural fluctuations on various time scales. At sufficiently long time, all structures associated with a substate are sampled and spectral diffusion is complete. All frequencies associated with the absorption band have been accessed. The 2D line shape goes from elongated to symmetrical. Fig. 2A shows that, by 48 ps, spectral diffusion is essentially complete. Here, we focus our analysis exclusively on the conformational switching; the protein structural dynamics that give rise to spectral diffusion of the A substates of MbCO have been reported previously (14, 29, 31).

Fig. 4.

Schematic illustration of a portion of the energy landscape of a protein, showing two substates and the finer energy landscape that exist in each of the minima. Transitions among the minima in one substate are responsible for structural fluctuations about the substate minimum. Transitions from one substate to another represent distinct structural configurational changes of the protein.

To quantitatively extract the time constant for the conformational switching from the 2D-IR spectra, the integrated peak volumes are fit to obtain the population of each species. The kinetic model described previously is used (15, 17, 20). It is possible to calculate the time evolution of the 2D spectrum including spectral diffusion and chemical exchange by using response function theory (20, 22, 23). However, in a detailed theoretical and experimental study, it was demonstrated that the exchange rate can be extracted by using the simpler method that is used here (20). Because spectral diffusion does not change the peak volumes, only their shapes, at each T_w the peak volumes were determined by fitting all of the peaks to 2D Gaussian functions (17, 20). The resulting fits provide the volume of each peak at each T_w. The conformational exchange causes the original peaks to decrease in volume and the cross peaks to increase in volume. In addition, the vibrational lifetime of the CO stretch, T₁, causes all of the peaks to decrease in volume. In previous applications of the 2D-IR vibrational echo chemical-exchange method to small molecules in liquids, it was also necessary to account for the orientational relaxation of the species (15, 17, 20). Here, the protein is so large that the slow orientational relaxation can be neglected.

Eq. 1 shows the kinetic scheme.

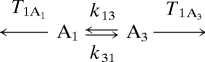By using IR pump–probe experiments, the vibrational lifetimes, T_1A1 and T_1A3, were measured. The lifetimes are 25 and 19 ps, respectively. Because the system is in thermal equilibrium, the rate of A₁ going to A₃, k₁₃[A₁], has to equal the rate of A₃ going to A₁, k₃₁[A₃]. The ratio of substates determined from FT-IR and IR pump–probe experiment is [A₁]/[A₃] = 0.9. The substate switching time constant from A₁ to A₃ is τ₁₃ = 1/k₁₃. Therefore, in fitting the data, there is only one adjustable parameter, the substate switching time, τ₁₃. There are eight peaks, four in the 0–1 region and four in the 1–2 region. The details of the fitting procedure have been presented previously (17, 20). The time-dependent volumes of all eight peaks are fit by using the single adjustable parameter, τ₁₃.

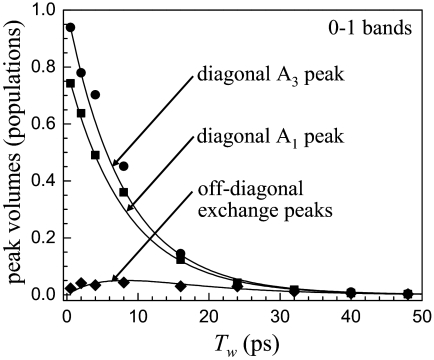
Fig. 2B shows calculated 2D spectra by using the known input parameters and the results of fitting τ₁₃. Both the measured and the generated spectra are normalized by making the largest peak equal to unity at each time. The calculated 2D spectra are in good agreement with the time-dependent 2D spectra for 0–1 and 1–2 transition regions. The experimental diagonal and off-diagonal peak volumes for the 0–1 region of the spectra are plotted in Fig. 3. The solid lines through the data points are obtained from the fitting procedure with τ₁₃ as the single adjustable parameter. The data from the 1–2 transition region can be reproduced with the identical parameters used for the 0–1 region. The fact that both the 0–1 and 1–2 regions can be fit with the same value of τ₁₃ demonstrates that the thermal equilibrium of the system is not perturbed by vibrational excitation of the CO stretch (17). The results of the fitting yield τ₁₃ = 47 ± 8 ps. Within experimental error, τ₁₃ = τ₃₁.

Fig. 3.

Peak volume data obtained from the fitting of the 2D-IR spectra of L29I-CO for the 0–1 transition region. The diagonal A₁ and A₃ bands as well as the off-diagonal peaks that grow in because of substate switching are fit with a single adjustable, the substate switching time, τ₁₃ = 1/k₁₃. The solid curves are the results of the fits, which yield τ₁₃ = 47 ps.

Although Mb is one of the most intensively studied proteins and a great deal of attention has been focused on the nature and dynamics of the substates (1–3, 7–9), previously it has not been possible to measure the conformational switching between the A₁ and A₃ substates. The growth of the cross peaks in the 2D-IR vibrational echo spectra provides a direct observation of the conformational exchange. The interconversion time of 47 ps is faster than, but consistent with, the rough estimates that were made previously (13, 14). Because the 3D structure of L29I mutant Mb has not been reported, the impact of the amino acid substitution on the protein structure and dynamics is not clear. However, the peak frequencies of the CO absorption bands of L29I are virtually identical to the peak frequencies of wild-type Mb. The frequencies of the CO peaks in the IR spectrum are very sensitive to the protein structure. The fact that L29I-CO and MbCO have the same peak frequencies demonstrates that the perturbation of the structure of the heme pocket is small.

By using a combination of vibrational echo experiments and MD simulations, aspects of the structural change associated with the conformational switching between the A₁ and A₃ substates were established (14). The structural difference between the substates that is most directly involved in the difference in frequency of the A₁ and A₃ absorption peaks involves the imidazole side group of the distal histidine (N_ε protonated) rotating about the C_βC_γ (methylene carbon-imidazole ring carbon) bond. Movement of the distal histidine, which brings the N_εH into closer proximity to the CO, gives rise to the A₃ substate (11, 14). The A₁ substate has the distal histidine in a configuration that places the N_εH further from the CO (14). In the absence of interactions between the imidazole and any other moiety, it would be possible for the imidazole side group of a histidine amino acid to rotate about the C_βC_γ bond without causing translation or reorientation of the remainder of the molecule. In the crowded environment of the heme pocket, this is not likely to be the case. Switching between the A₁ and A₃ substates changes the interaction of the His-64 imidazole side group with the heme-CO and other moieties (see Fig. 1A). The change in the interactions should cause the His-64 to slightly reorient and translate. The structures of the heme pocket for the A₁ and A₃ substates taken form the MD simulation are shown in figure 5 of ref. 14. In these figures, which are single snap shots of the A₁ and A₃ structures, it is evident that with the rotation of the imidazole ring by ≈40° around the C_βC_γ bond there is also a change in the alignment of the C_αC_β bond relative to the heme. These considerations suggest that there is a change in the geometry of the E helix (see Fig. 1A) in going between the A₁ and A₃ substates.

That significant structural change occurs in the A₁–A₃ interconversion is supported by x-ray experiments. The high-resolution crystal structure of MbCO that contains two conformations has enabled modeling of the structure of A₁ and A₃ substates (11, 32). Although the distal histidine has a critical role in determining the substates of Mb, structural comparison between the A₁ and A₃ substates shows that the A₃ substate contains an additional cavity, Xe3, and another transient cavity found in simulations (32). Xe is used as a probe to identify the locations of cavities in proteins (33, 34). In Mb crystals, four Xe atoms (Xe1, Xe2, Xe3, and Xe4) occupy cavities, which may be involved in gas ligand migration (32, 33). The Xe3 site, which is near the surface and far from the iron atom, involves Trp-7 and is located between helices E and H (33). The existence of Xe3 in the A₃ substate but not in the A₁ substate demonstrates that the difference in the substates is significantly more than the rotation of the imidazole side group of the distal histidine.

The fast time constant for interconversion, 47 ps, is in line with the structural difference between the A₁ and A₃ substates. Incoherent quasielastic neutron scattering experiments on native bovine α-lactalbumin observed collective motions on the tens of picosecond to 100-ps time scale (35). The correlation length for such fluctuations was reported to be 18 Å (35). The switching time observed here falls into this time range, which is consistent with a reconfiguration of the E helix in the interconversion between the A₁ and A₃ substates.

Concluding Remarks

NMR techniques probe protein motions in the microsecond, millisecond, and longer time scales (36). Conformational switching processes studied by NMR involve large structural changes that occur, for example, in enzyme catalytic processes (37). Such structural changes require the reconfiguration of many amino acids, helices, and various protein structures. To place in a broader context the time-dependent measurements of substate switching presented here, a single elementary structural change, it is useful to discuss the kinetics of large-scale structural changes in terms of the ideas of linear response. Linear response theory describes how thermal fluctuations and elementary steps bring a system into a new configuration.

The concept of linear response comes from the fluctuation dissipation theorem (38). It states that a system in thermodynamic equilibrium has a response to a small perturbation with a time dependence determined by the equilibrium fluctuations of the system. The time-dependent fluorescence Stokes shift experiment is a well studied example of relaxation to a new equilibrium structure after a perturbation (39). In the experiment, a solute molecule with a small or zero permanent dipole moment in the ground electronic state is excited to the first excited state that has a large dipole moment. The local solvent structure will evolve to produce a net alignment of the solvent dipoles relative to the newly created large solute dipole. The orientational alignment of the solvent dipoles occurs in the same manner as thermal equilibrium orientational relaxation. (Translational relaxation will also occur.) Before the generation of the solute dipole, the solvent molecules are executing angular random walks (orientational diffusion). The sudden presence of the solute dipole slightly biases the random walks toward alignment. The alignment of a single solvent dipole can be viewed as an elementary step in the restructuring of the solvent. The solvation of the solute dipole requires the combined response of many solvent molecules.

Fig. 4 displays a schematic of a portion of the energy landscape of a protein having two substates. Each substate minimum is actually a broad rough landscape with many local minima separated by barriers of varying heights. Transitions between these minimum are responsible for protein structural fluctuations about a specific structure associated with a particular substate minimum (1–3). These fluctuations can vary in time scales from subpicosecond to tens and hundreds of picoseconds to much longer (1–3). The fluctuations range from the fastest motions involving just a few atoms to low-frequency acoustic-type modes of the entire protein. The distinction between structural fluctuations that come from making transitions among the minima on the landscape of a particular substate and transitions between substates is in some sense operational. A substate has a structural aspect that is qualitatively distinct. Fluctuations make interconversions among substates possible by sampling the energy landscape in a particular substate and bringing the protein to the transition state between substates.

When a protein experiences a perturbation such as substrate binding or a temperature jump that induces folding or unfolding, in accord with linear response, it will respond to the perturbation by fluctuation-driven elementary steps (substate changes) that can occur in the absence of the perturbation. However, the sampling of the substates will be biased by the perturbation, and the protein will relax to a new structure. The protein is always executing a multidimensional walk among substates. The walk will be skewed by the perturbation. The skewing can result from the shifting of substate minima and barriers. The relaxation to the new structure can be slow because it requires many elementary steps. A slow response to a perturbation results from structural fluctuation sampling that produces elementary steps, which in turn combine to produce major restructuring.

Here, by using ultrafast 2D-IR vibrational echo chemical-exchange spectroscopy, we have measured the time dependence of a single elementary step, the A₁–A₃ substate switching. The time constant for the substate switching is 47 ps. The concept of conformational substates in proteins was introduced in 1974 (3). In 1987, MD simulations of Mb for 300 ps confirmed the existence of multiple conformational states (40). The rapid advance of computer technology makes simulations of protein dynamics for much longer time scales readily doable. The A₁–A₃ substate switching time reported here will be an important target for future MD simulations because the barrier crossing will need to be simulated accurately. Simulations will determine whether the dynamics of real systems undergoing an elementary structural change can be reproduced, and they will provide details of the structural changes that accompany the A₁–A₃ interconversion.

Materials and Methods

Expression and purification of the mutant sperm whale Mb L29I were performed as described in ref. 41. The CO forms of mutant Mb was prepared according to published protocols (14). For both the linear FT-IR and vibrational echo measurements, ≈20 μl of the sample solution was placed in a sample cell with CaF₂ windows and a 50-μm Teflon spacer. The 2D-IR vibrational echo experiments were described briefly above, and full details have been published previously (17, 19, 29, 42).