The Relationship between Single-Channel and Whole-Cell Conductance in the T-type Ca²⁺ Channel Ca_V3.1

Abstract

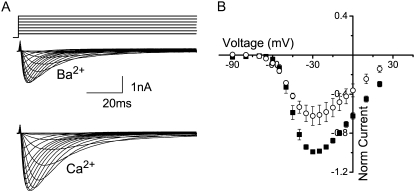
In T-type Ca²⁺ channels, macroscopic I_Ba is usually smaller than I_Ca, but at high Ca²⁺ and Ba²⁺, single-channel conductance (γ) is equal. We investigated γ as a function of divalent concentration and compared it to macroscopic currents using Ca_V3.1 channels studied under similar experimental conditions (TEA_o and K_i). Single-channel current-voltage relationships were nonlinear in a way similar to macroscopic open-channel I/Vs, so divalent γ was underestimated at depolarized voltages. To estimate divalent γ, concentration dependence, i_Div, was measured at voltages <−50 mV. Data were well described by Langmuir isotherms with γ_max(Ca²⁺) of 9.5 ± 0.4 pS and γ_max(Ba²⁺) of 10.3 ± 0.5 pS. Apparent K_M was lower for Ca²⁺ (2.3 ± 0.7 mM) than for Ba²⁺ (7.9 ± 1.3 mM). A subconductance state with an amplitude 70% that of the main state was observed, the relative occupancy of which increased with increasing Ca²⁺. As predicted by γ, macroscopic G_maxCa was larger than G_maxBa at 5 mM (G_maxCa²⁺/Ba:²⁺1.43 ± 0.14) and similar at 60 mM (G_maxCa²⁺/Ba:²⁺1.10 ± 0.02). However, over the range of activation, I_Ca was larger than I_Ba under both conditions. This was a consequence of the fact that V_rev was more negative for I_Ba than for I_Ca, so that the driving force determining I_Ba was smaller than that determining I_Ca over the range of potentials in standard current-voltage relationships.

INTRODUCTION

T-type Ca²⁺ channels are characterized by their low threshold of activation, tiny single-channel conductance, and slow deactivation (1–3). The three cloned isoforms, Ca_V3.1–3.3, display a broad tissue distribution, where they play both an electrogenic role, by contributing to depolarization, and a regulatory role, by providing a pathway for Ca²⁺ influx. Ca²⁺ entry into cells can have profound effects on cellular function, because intracellular Ca²⁺ levels control the activation of Ca²⁺-dependent proteins and channels. T-type Ca²⁺ channels, in particular, are thought to produce a steady influx of Ca²⁺ near the resting membrane potential, allowing them to contribute to the generation of low-threshold Ca²⁺ spikes, pacemaking, rebound burst firing, and low-amplitude Ca²⁺ oscillations (for review, see (3)). Ca²⁺ flux through these channels also produces local changes in Ca²⁺ that affect the activity of nearby Ca²⁺-dependent proteins; for example, they have been shown to be functionally coupled to Ca²⁺-activated K channels (4). Studies of mice deficient in Ca_V3.1 have implicated these channels in absence seizures, sinoatrial node pacemaker activity, atrioventricular conduction, and sleep disorders (5–7).

Elucidating the details of ion conduction in Ca²⁺-dependent channels will help in understanding how they contribute to the various physiological functions in which they are thought to be involved, and in understanding structural determinants that vary between high- and low-voltage-activated channels. Although single-channel measurements provide a direct measure of ion conduction, in T-channels, conductance measurements have varied from 6 to 11 pS in high Ba²⁺. Furthermore, whole-cell and single-channel recordings have provided conflicting reports about the relative size of currents in the presence of Ba²⁺ versus Ca²⁺. For the most part, single-channel recordings in T-channels have reported similar values of conductance for Ca²⁺ and Ba²⁺ (1,8–11), whereas macroscopic recordings have reported Ca²⁺ currents either larger than or of similar size to Ba²⁺ currents (e.g., (12–15)). Two of the possible explanations for these discrepancies are 1), the measurements have been made using different divalent concentrations; typically, single-channel recordings have been made using very high divalent concentrations (>60 mM), whereas whole-cell recordings have been made at much lower divalent concentrations (typically <20 mM). 2. Single-channel recordings for T-channels have been performed primarily in tissues in which multiple T-channel isoforms are present, whereas whole-cell recordings have been performed both in native cells and in heterologous expression systems with individual isoforms. Three groups have suggested that the individual isoforms display differences in the relative magnitude of the whole-cell currents in the presence of Ba²⁺ and Ca²⁺ (13,16,17).

Here, we have explored the relationship of the concentration dependence of single-channel conductance to macroscopic currents. We performed these studies using an individual isoform of the T-channel, Ca_V3.1, to exclude any potential isoform differences. In addition, we measured the ion dependence of single-channel conductance and macroscopic currents in Ca²⁺ and Ba²⁺ under similar experimental conditions to eliminate, as much as possible, differences that might arise from interactions with other extracellular or intracellular cations. Both single-channel current-voltage relationships (I/Vs) and macroscopic open-channel I/Vs, were highly nonlinear, and the conductance measured from −20 mV to −60 mV was ∼2-fold smaller than that measured from −60 mV to −120 mV. The concentration dependence of conductance measured over a negative voltage range, where divalent flux predominates and the current-voltage relationship is more highly linear, were well described by Langmuir isotherms, with γ_max(Ca²⁺) of 9.5 ± 0.4 pS and γ_max(Ba²⁺) of 10.3 ± 0.5 pS. Apparent K_M was lower for Ca²⁺ (2.3 ± 0.7 mM) than for Ba²⁺ (7.9 ± 1.3 mM). A subconductance state whose amplitude was 70% that of the main state was observed, and its relative occupancy increased with increasing Ca²⁺. As predicted by the K_M difference between Ca²⁺ and Ba²⁺, macroscopic G_maxCa was larger than G_maxBa at 5 mM (G_maxCa²⁺/Ba²⁺ = 1.43 ± 0.14) and similar at 60 mM (G_maxCa²⁺/Ba²⁺ = 1.10 ± 0.02). However, over the range of activation, I_Ca was larger than I_Ba under both conditions. This was a consequence of the fact that for I_Ba, V_rev was more negative than for I_Ca, so that the driving force determining I_Ba was smaller than that for I_Ca over the range of potentials in standard current-voltage relationships.

MATERIALS AND METHODS

Heterologous expression

Central to being able to study the relationship between whole-cell and single-channel amplitudes is the availability of cells expressing variable numbers of channels so that voltage control can be achieved over a wide range of permeant cation concentrations. Three stable cell lines expressing Ca_V3.1 were created to provide such a range of channel expression levels. Ca_V3.1 exists in a number of splice variants (18). Here, we used the 217 isoform, which is one of the two most prevalent isoforms of Ca_V3.1 in the human adult brain. It differs from the other highly abundant 89 isoform by only 23 amino acids in the 2-3 linker (18). The cDNA Ca_V3.1 217 was kindly provided by M. C. Emerick and W. S. Agnew (The Johns Hopkins University School of Medicine, Baltimore, MD). It was subcloned into 1), pcDNA3.1/Zeocin and stably expressed in HEK-293 cells; 2), pDNA5/FRT and stably expressed in HEK293/FLP cells; and 3), pcDNA5/FRT/TO and stably expressed in Flp-In T-REx-293 cells (Invitrogen, Carlsbad, CA). Stable cell lines were created using either 200 μg/ml Zeocin for HEK-293 cells or 100 μg/ml HygroGold for HEK293/FLP cells and T-REx-293 cells. Cells were maintained in 100-mm Corning culture dishes in Dulbecco's modified Eagle's medium (Invitrogen) supplemented with 10% fetal bovine serum, 1% penicillin-streptomycin, and either 100 μg/ml Zeocin (for HEK-293 cells) or 50 mg/ml HygroGold (for HEK293/FLP), or 1% L-glutamine, 15 μg/ml blasticidin, and 50 μg/ml HygroGold (for T-REx-293 cells). Ca_V3.1 expression in T-REx-293 cells was induced with 0.005–0.2 μg/ml tetracycline, depending on the desired channel density, 18 h before use in electrophysiology experiments. Differences in channel density across cell lines were associated with predictable differences in the probability of observing single-channel, multichannel, or macropatch currents.

Solutions and chemicals

For single-channel experiments, the bath solution contained (in mM) 150 KCl and 10 HEPES, titrated to pH 7.4 with KOH to depolarize cells to 0 mV for on-cell patch recording. In some cases, 1 mM CaCl₂ was added to the bath solution, which tended to improve seal resistances. The pipette solution contained (in mM) 5, 10, 20, 40, or 60 CaCl₂ or BaCl₂; 150, 145, 130, 100, 50, or 0 TEACl; and 10 HEPES, titrated to pH 7.4 with TEAOH.

For whole-cell experiments, the bath solutions were the same as for single-channel pipette solutions. The pipette solution for the 5-mM divalent experiments contained (in mM) 140 KCl, 1 CaCl₂, 11 EGTA, 5 MgATP, and 10 HEPES, titrated to pH 7.4 with KOH. For the 60-mM divalent experiments, the pipette solutions contained (in mM) 140 KCl, 1 CaCl₂, 11 EGTA, and 10 HEPES, titrated to pH 7.4 with KOH; MgATP was not included because it formed insoluble complexes when in contact with Ba²⁺.

Electrophysiology and analysis

All recordings were made using an Axopatch 200B feedback amplifier (Molecular Devices, Sunnyvale, CA) with a Digidata 1321A digitizer and pClamp 8.1 data acquisition software (Molecular Devices). Recordings were made at room temperature (20–26°C) using whole-cell or cell-attached voltage clamp of trypsinized cells (0.25% Trypsin-EDTA, Invitrogen or Sigma-Aldrich, St. Louis, MO) 3–5 days after plating.

Whole cell recordings

Whole-cell recordings used pipettes pulled from thin-walled borosilicate glass capillaries (World Precision Instruments, Sarasota, FL) using a Flaming/Brown micropipette puller P97 (Sutter Instruments, Novato, CA). Resistances were 0.7–1.3 MΩ when filled with pipette solution. Holding potential was −110 mV and cells were depolarized once every 5 s to ensure full recovery from inactivation. Standard current-voltage protocols stepped to increasingly positive potentials between −90 and 40 mV for 100–200 ms. Currents were digitized at 10 or 20 kHz and filtered at 5 kHz by an 8-pole low-pass Bessel filter. For open-channel current-voltage protocols, currents were digitized at 200 kHz and filtered at 100 kHz by an 8-pole low-pass Bessel filter. Cells were depolarized for 1 ms to 60 mV for 5-mM divalent experiments and to 115 mV for 60-mM divalent experiments, then stepped to a range of potentials (−120 mV to +120 mV). Cells were depolarized once every 5 s and the current was measured as the peak current after the depolarization. A more positive depolarization voltage was selected for the high divalent condition because of the positive shift in activation under the high divalent condition. Similar results were obtained using 1.2- or 1.5-ms depolarization durations and cells were excluded from analysis if the time to peak of the current at −120 mV was >300 μs. Ionic current data were capacity-corrected using 8–16 subthreshold responses (voltage steps of −10 or −40 mV) and leak-corrected, based on linear leak resistance calculated at potentials negative to −80 mV or by linear interpolation between the current at the holding potential and 0 mV. The data were analyzed using locally written programs in MATLAB (The Math Works, Natick, MA) and Origin software (OriginLab, Northampton, MA).

Single-channel recordings

Patch pipettes were constructed from 1.2-mm quartz glass capillary tubes (Sutter Instruments) using a P-2000 laser puller (Sutter Instruments). A few early patch recordings used pipettes pulled from thin-walled borosilicate glass capillaries. Borosilicate patch pipettes were fire-polished with a Narishige (Tokyo, Japan) microforge and coated with SigmaCote (Sigma-Aldrich). Pipettes had resistances of 5–18 MΩ for single-channel recording. Single-channel data were filtered at 2 kHz using an 8-pole low pass Bessel filter and sampled at 20 kHz or 4 kHz.

Patches were held at −100 mV and single-channel currents were recorded during either 100-ms step depolarizations between −70 and 0 mV or 80-ms steps to potentials between −50 and −120 mV immediately after a 3-ms depolarization to 0 mV. In high divalent concentrations, the voltage of the brief depolarization was increased to +20 or +30 mV to increase the probability that channels would open. For each voltage protocol, pulses were applied every 3 s to maximize channel availability.

Even though HEK293 cells are relatively electrically quiet, patches occasionally contained endogenous channels. Several different methods were used to ensure that patches contained activity consistent with Ca_V3.1 and not endogenous channels. Contamination by endogenous channels was reduced by the use of extracellular TEA, and patches containing activity at the holding potential were excluded. Furthermore, endogenous currents were identified by examining the characteristics of currents from parent cells not expressing Ca_V3.1. Patches containing activity similar to that of parent cells were excluded from recording and analysis. Endogenous channels observed in parent cells, when present, were active over a large range of potentials and were not preferentially activated in response to voltage steps. They varied in magnitude and event duration, but some commonly observed events were several milliseconds to tens of milliseconds in duration and were typically >2 pA in size at −100 mV, i.e., longer in duration and larger in size than T-channel currents. As a last step before accepting the patches for recording, they were depolarized for a small number of sweeps over a range of potentials to visually identify the presence of T-channel activity. The criteria applied to identify T-channel-containing patches were 1), currents were inward; 2), currents could be detected around −70 mV or more positive for high divalent concentrations; 3), as the potential was increased from threshold, the events occurred closer to the onset of the voltage step and with greater frequency; and 4), the currents were <2 pA. In addition to excluding patches at the time of recording, patches that contained activity inconsistent with T-channel activity were excluded during offline analysis.

Currents displayed are always capacity- and leak-corrected and include 15 ms at the holding potential preceding the voltage step. Currents were capacity-corrected by subtracting the average of current records containing no channel activity (nulls). The average null current records were linearly scaled to the appropriate voltage if necessary. Current records were leak-corrected by subtracting the average current in the last millisecond at each potential. In addition, the baseline was adjusted manually on a sweep-by-sweep basis if necessary. Only patches with seal resistance >50 GΩ were used for analysis.

The data were analyzed using locally written programs in MATLAB and Origin software. Current amplitudes were measured by constructing all-points histograms from selected segments of active sweeps. Events were identified by eye, with a bias against simultaneous openings. The segments of data surrounding each event were manually selected; data were concatenated and used to generate amplitude histograms. All-points histograms were constructed from the concatenated data using a bin width of 30–100 fA, depending on the bit resolution of the recording, which was usually 16 fA, and the histograms were fit with the sum of two Gaussians. This method excluded excess closed-state data and enhanced the relative size of the open-state peak in the amplitude histogram and thereby the accuracy of the fits, although with this method the size of the closed- and open-state peaks bears no relationship to mean closed and open lifetimes, respectively. In some cases, current amplitudes were measured using software based on a hidden Markov model (QuB, SUNY at Buffalo, Buffalo, NY) to assess the contribution of a subconductance state. In these cases, the concatenated selected segments were idealized using the SKM algorithm (19,20). For both methods, conductance was determined by linear regression to the currents from multiple patches at each concentration and expressed as the standard error of the estimate.

The SKM algorithm method of idealization is a much more sensitive technique than all-points histograms for measuring both single-channel current amplitudes and relative occupancies of each conductance state. To assess the limitations of idealizing the data using this algorithm, simulations were performed using varying signal/noise ratios. The amplitudes of the simulated data were estimated accurately with signal/noise ratios as low as 2 and with only small attenuation with signal/noise ratios as low as 1. However, at signal/noise ratios of 2 and lower, there was an increase in the number of missed events and overestimation of the average lifetime of the events. One advantage of this method of idealization is that it is not very model-dependent; it is only dependent on the number of conductance states in the model and is not sensitive to the connectivity of these states.

RESULTS

T-channels have been reported to have the same single-channel conductance in high concentrations of Ba²⁺ and Ca²⁺ (1,8–11), although several groups have measured macroscopic Ca²⁺ currents to be larger than Ba²⁺ currents in experiments performed with heterologously expressed Ca_V3.1 (16,21,22), and others have observed Ca²⁺ and Ba²⁺ currents of the same magnitude (12,23). In our hands, when currents measured in 5 mM Ba²⁺ were compared with those in 5 mM Ca²⁺, the macroscopic currents in the presence of Ba²⁺ were ∼40% smaller than those in the presence of 5 mM Ca²⁺ (Fig. 1). For these experiments, we measured the Ca²⁺ and Ba²⁺ currents in the same cell and varied the order in which the conditions were studied. The extracellular solutions contained the impermeant cation, TEA⁺, and K⁺ was the intracellular monovalent in each case to match the recording conditions that we subsequently used for the single-channel recording. Although there are several possible explanations for the differences in whole-cell current magnitudes, here we addressed to what extent these differences could be a consequence of a difference in the concentration dependence for single-channel conductance under the two divalent conditions.

FIGURE 1.

(A) Family of representative whole-cell currents from the same cell in the presence of 5 mM Ba²⁺ (middle) and 5 mM Ca²⁺ (lower) in response to 5-mV voltage steps from a holding potential of −110 mV over the range −90–+40 mV. Cells were depolarized once every 5 s to ensure full recovery from inactivation. (B) Average ± SE of the current-voltage relationship in the presence of 5 mM Ba²⁺ (circles) and Ca²⁺ (squares) for five cells studied in the same way. Currents were normalized to the peak Ca²⁺ current in each cell.

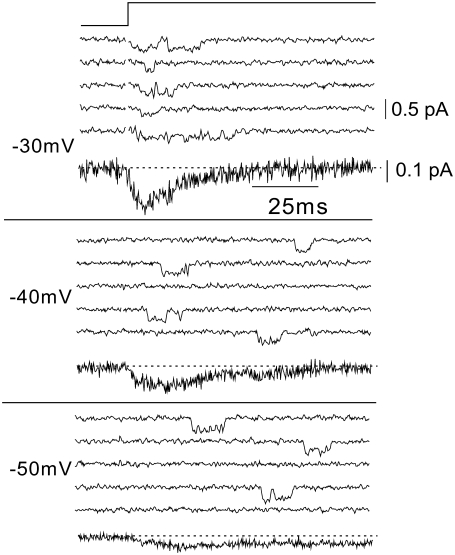
In cell-attached recordings with 20 mM Ca²⁺, events were detectable across a range of potentials. Fig. 2 shows sample currents at −30, −40, and −50 mV. T-channel events were detected at a lower frequency and with longer latency at −50 mV compared to −30 mV. The number of active sweeps also increased with increasing depolarization. We used criteria described in the Methods to confirm that these events were in fact T-type currents, and ensemble traces shown in Fig. 2 are characteristic of T-channel currents. The signal/noise ratio decreased at more positive potentials, but even with a 2-kHz bandwidth the ratios were typically ∼2.5 at −30 mV and ∼5 at −50 mV with the 200B amplifier and quartz pipettes.

FIGURE 2.

Representative single T-type Ca²⁺ channel currents and ensemble averages. Capacity- and leak-corrected single-channel currents and the corresponding ensemble currents from a single cell-attached patch elicited with step depolarizations to the indicated potentials (left) in the presence of 20 mM Ca²⁺. Currents shown include 15 ms at the holding potential (−100 mV) and 100 ms at the depolarized potential. Currents were sampled at 20 kHz, filtered at 2 kHz, and then downsampled to 4 kHz offline. For graphical purposes, traces were additionally filtered by adjacently averaging by 3. The seal resistance of the patch was >100 GΩ.

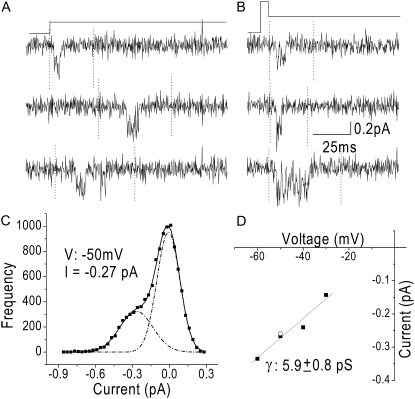
To maximize the voltage range over which channel amplitude could be measured and to enhance the signal/noise ratio, we also measured events in steps to hyperpolarized potentials after opening channels with a brief depolarization (tails). Fig. 3 compares single-channel current measurements made using step depolarizations and tail currents. Single-channel currents elicited with a step depolarization to −50 mV were similar to those elicited with tail-current protocols, which consisted of brief depolarizations to 0 mV followed by a hyperpolarization, as illustrated in this case, to −50 mV (Fig. 3, A and B). Current amplitude was measured from all-point amplitude histograms constructed from selected segments of active traces (∼100–200); a representative amplitude histogram for the data in Fig. 3 A is shown in Fig. 3 C. Single-channel conductance was taken as the slope of the single-channel current-voltage relationship (Fig. 3 D). The two points at −50 mV are current amplitudes measured with a step depolarization and a tail-current protocol, demonstrating that both methods gave similar values for single-channel current amplitudes.

FIGURE 3.

Measured current amplitudes are the same when currents are elicited using depolarizations or tail-current protocols. (A) Capacity- and leak-corrected single-channel currents from a cell-attached patch elicited with a 50-mV step depolarization (−100 mV to −50 mV) with 20 mM Ca²⁺ as the permeant ion. Data were sampled at 20 kHz, filtered at 2 kHz, and downsampled to 4 kHz offline. (B) Capacity- and leak-corrected single-channel currents from the same patch as in A elicited with the tail-current protocol shown above. Patches were depolarized to 0 mV for 3 ms and subsequently hyperpolarized for 80 ms, in this case to −50 mV. Single-channel current amplitudes were determined from all-points histograms from selected segments of active traces. Selected segments were marked (dotted lines) from ∼100 sweeps per potential, concatenated, and used to generate the amplitude histogram. The data were binned into 30-fA bins and fit with a sum of two Gaussians. The signal/noise ratio was ∼3 at −30 mV and increased to ∼7 at −50 mV. (C) Amplitude histogram for currents elicited with 50-mV step depolarizations. The dotted black lines are the Gaussian fit of the closed and open states, and the solid line is the sum of the Gaussians. The open-channel current at −50 mV was measured to be −0.27 pA. The area under the curve bears no relationship to open and closed durations, because the data used to generate the amplitude histogram excluded much of the closed-state data. (D) The current-voltage relationship for the patch shown in A and B. The solid line is a linear fit to the data with a slope conductance of 5.9 ± 0.8 pS. The two points at −50 mV were calculated using the protocols from A and B.

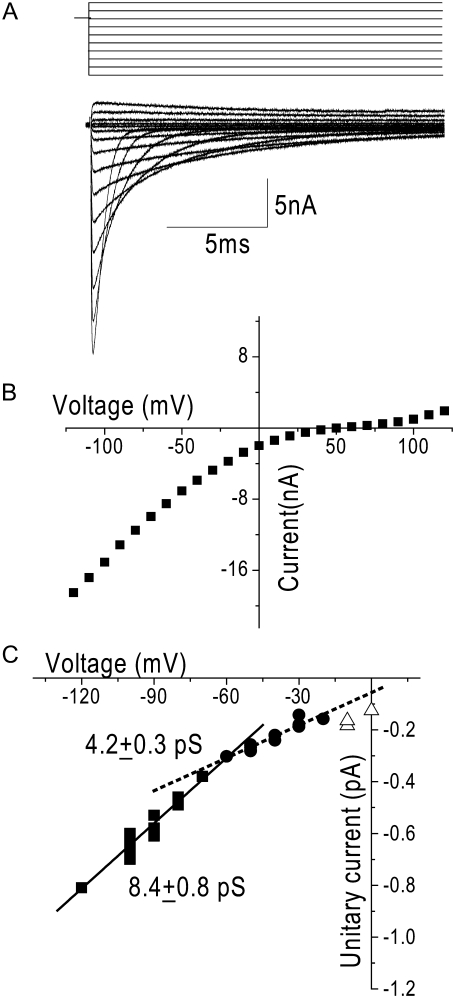
Under the same ionic conditions as the single-channel recordings, at positive potentials, T-channels pass outward monovalent currents that produce nonlinear open-channel current-voltage relationships with the outward monovalent currents being carried K⁺ in this case (Fig. 4 B). Nonlinearity was also apparent in the single-channel current-voltage relationship measured under the same ionic conditions across a wide voltage range (0 to −120 mV) (Fig. 4 C). This nonlinearity of the current-voltage relationship made the measurement of slope conductance highly sensitive to the voltage range over which it was measured. A linear fit to the data between −20 mV and −60 mV (Fig. 4 B, dotted line) yielded a conductance that was half that measured over the more negative voltage range (from −60 to −120 mV, Fig. 4 B, solid line) (γ_{−20 to −60} = 4.2 ± 0.3 pS versus γ_{−60 to −120} = 8.4 ± 0.8 pS). To more accurately estimate divalent conductance, therefore, all measurements were made over a voltage range far from the reversal potential; i.e., negative to −50 mV, a voltage range over which the single-channel current-voltage relationship was maximally linear (in which divalent flux predominates) and where the signal/noise ratio is relatively large.

FIGURE 4.

Nonlinearity of the whole-cell and single-channel current-voltage relationships at positive potentials. (A) Family of capacity- and leak-corrected representative currents recorded during steps between −150 mV and 130 mV immediately after a 1-ms depolarization to 0 mV from a holding potential of −100 mV. Sweeps are shown for every 20 mV. (B) Representative whole-cell open-channel I/V relationship for the cell in A. For whole-cell experiments, the bath solution was the same as the 20-mM-Ca²⁺ single-channel pipette solution, and the pipette solution contained (in mM) 140 KCl, 1 CaCl₂, 10 EGTA, 5 MgCl₂, and 10 HEPES, titrated to pH 7.4 with KOH. Data were filtered at 100 kHz by an 8-pole lowpass Bessel filter and digitized at 200 kHz. Although the currents are rather large, the time to peak of the tail currents was within the same range as that of currents of much smaller amplitude (0.15 ms) indicating that voltage control was maintained (data not shown). (C) Single-channel current-voltage relationship. Currents shown are from eight different patches in 20 mM Ca²⁺. Tail protocols were used to elicit currents from −70 to −120 mV and 100-ms step depolarizations were used from 0 to −70 mV, where each symbol represents an individual determination from a single patch. Single-channel conductance was highly sensitive to the voltage range over which it is measured. The dotted line is a linear fit to the data between −20 mV and −60 mV (γ = 4.2 ± 0.3 pS) (solid squares). The solid line is a linear fit of the data between −60 mV and −120 mV (γ = 8.4 ± 0.8 pS) (solid circles).

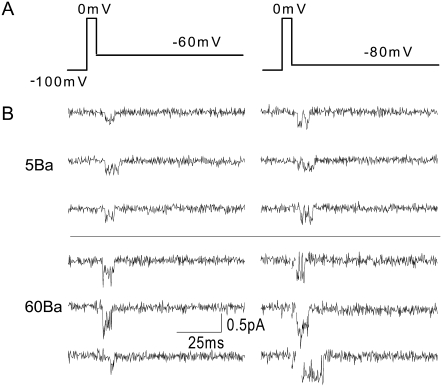
T-channels are also permeable to Ba²⁺ ions and have been shown to conduct Ca²⁺ and Ba²⁺ equally well at high divalent concentrations (1,8–11). Fig. 5 B shows sample Ba²⁺ currents at 5 and 60 mM, which were recorded using the tail-current protocol shown in Fig. 5 A. As expected, currents were larger in higher divalent concentrations and at more negative potentials.

FIGURE 5.

Representative single-channel Ba²⁺ currents. (A) Voltage protocol used to elicit single-channel currents in B and C. Patches were held at −100 mV, depolarized to 0 mV for 3 ms, and then hyperpolarized to the test potential. Recordings were made during the final 15 ms of the 3-s interpulse interval, during the 3-ms depolarization to 0 mV, and for 80 ms at the test potential. (B) Capacity- and leak-corrected single-channel currents elicited with the tail protocol shown in A from a holding potential of −100 mV in 5 mM Ba²⁺ (upper) and 60 mM Ba²⁺ (lower). Top currents were sampled at 4 kHz and filtered at 2 kHz. Bottom currents were sampled at 20 kHz and filtered at 2 kHz and then downsampled to 4 kHz offline. The seal resistance was >100 GΩ in each patch.

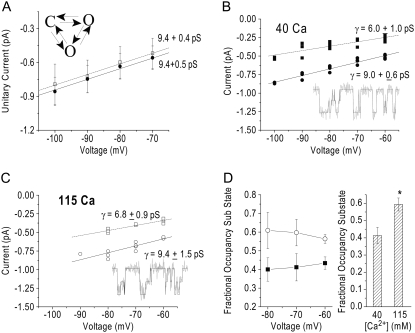
As we measured the concentration dependence of single-channel conductance, we found that with 115 mM Ca²⁺ patches were much less stable, and when measuring the current amplitude, we observed that histograms were not well fit by the sum of two Gaussians. Rather, there appeared to be an additional conductance state present that was affecting our estimate of conductance. Several single-channel studies in T-channels have reported the presence of subconductance events in these channels (1,9,10,24–26). To identify the subconductance state, we needed to find a more sensitive analysis technique to analyze the data. We chose a hidden Markov method (QuB), idealizing the data using the SKM algorithm. This method can be used to accurately estimate single-channel current amplitudes with signal/noise ratios as low as 2. Before using QuB to analyze the 115 mM Ca²⁺ data, we compared the measurements of current amplitudes using QuB to those measured using amplitude histograms at a concentration of Ca²⁺ (40 mM) where all-points amplitude histograms adequately estimated current amplitudes when event selection was biased against obvious subconductance behavior. For QuB analysis, entire traces were selected to ensure inclusion of subconductance activity that might not be appreciated by eye. Fig. 6 A shows current amplitudes measured for patches using histogram analysis (open circles) and QuB (solid circles). The main-state conductance measured using each method was not significantly different (9.0 ± 0.6 for QuB and 9.5 ± 0.4 for histogram analysis).

FIGURE 6.

(A) Single-channel currents as a function of potential measured using an amplitude histogram (open circles, n = 4) or QuB (solid squares, n = 5), as described in text, using the diagram of the model shown. (B) Current-voltage relationship for both the main conductance state (solid circles) and subconductance state (solid squares) obtained using QuB in the presence of 40 mM Ca²⁺ (n = 5). The solid line is a linear fit of the main-state data with a slope conductance of 9.0 ± 0.6 pS. The dotted line is a linear fit of the subconductance-state data with a slope conductance of 6.0 ± 1.0 pS. (Inset) Idealized currents in the presence of 40 mM Ca²⁺. Currents were sampled at 20 kHz, filtered at 2 kHz, and downsampled offline to 4 kHz. (C) The current-voltage relationship for both the main conductance state (open circles) and subconductance state (open squares) obtained using QuB in the presence of 115 mM Ca²⁺ (n = 4). The solid line is a linear fit of the main-state data with a slope conductance of 9.4 ± 1.5 pS. The dotted line is a linear fit of the subconductance-state data with a slope conductance of 6.8 ± 0.9pS. (Inset) Idealized currents in the presence of 115 mM Ca²⁺. Currents were sampled at 20 kHz, filtered at 2 kHz, and downsampled offline to 4 kHz. (D, left) The relative fractional occupancy of the subconductance states for 40 mM Ca²⁺ (solid squares) and 115 mM Ca²⁺ (open circles). Fractional occupancy was calculated as (occupancy of the subconductance state)/(occupancy of the subconductance state + occupancy of the main conductance state). (D, right) The grouped relative fractional occupancy of the subconductance state for 40 mM Ca²⁺ (n = 5) and 115 mM Ca²⁺ (n = 4). The data from each cell over a voltage range of −60 mV to −80 mV were averaged and the values from each cell were averaged and displayed as mean ± SE. *—Statistical significance as measured by a Student t-test (p = 0.03).

To determine whether currents contained significant subconductance activity, we analyzed events in the presence of 115 mM Ca²⁺ and in 40 mM Ca²⁺ using a three-state model containing two open states in QuB (Fig. 6 A). The model shown is not representative of a detailed kinetic model for T-channels. One of the advantages of using the SKM algorithm in QuB to idealize that data is that it is not very model-dependent; it is only dependent on the number of conductance states in the model and is not sensitive to the connectivity of these states. In both 40 mM and 115 mM Ca²⁺, we were able to reliably detect a main state and a subconductance state (Fig. 6, B and C), and the conductance of these states in 40 mM and 115 mM Ca²⁺ were similar. The relative occupancy in the subconductance state did not vary as a function of the potentials studied (Fig. 6 D, left). However, the relative occupancy of the subconductance state was higher in the presence of 115 mM Ca²⁺ than in 40 mM Ca²⁺ (Fig. 6 D, right).

Although our method for measuring single-channel currents precluded our ability to perform a thorough kinetic analysis of these states, the average lifetime measurements obtained using the SKM idealization indicated that the ratio of the average lifetime of the subconductance state to the average lifetime of the main state was higher in 115 mM Ca²⁺ than in 40 mM Ca²⁺ (1.01 ± 0.13 for 115 mM and 0.66 ± 0.09 for 40 mM). The lifetime estimates of the main state ranged from 0.6 to 1.8 ms in 115 mM and from 0.6 to 1.4 ms in 40 mM. In general, additional filtering and resampling of the data only very slightly reduced the amplitude of both states but significantly increased the lifetimes, as is expected for overfiltering of fast gating events. Filtering at 1 kHz only slightly affected the relative ratio of the lifetime subconductance state to the lifetime of the main state under both conditions (0.94 ± 0.14 in 115 mM and 0.54 ± 0.07 in 40 mM), indicating that we were not simply measuring open-channel noise as subconductance states. Furthermore, the open-channel noise was similar for both the main state and the subconductance state and was only slightly more than the closed-channel noise (typical differences were 0.01–0.04 pA). Although the average lifetime measurements cannot be interpreted as accurate estimates of lifetimes, since they were taken from tail-current measurements where the channels were usually already open at the beginning of the selected event, they do suggest that increased Ca²⁺ concentrations increased the relative lifetime of the subconductance state.

We also attempted to examine the relative occupancy of the subconductance state in the presence of high concentrations of Ba²⁺, but we were unable to reliably measure a subconductance level under these conditions. It seems likely that a subconductance state is visited when Ba²⁺ permeates, because these states could be seen by eye, but either the lifetime of the state is too short to be reliably measured or the subconductance state is visited more rarely under these conditions. The conductance measured in 115 mM Ba²⁺ using an all-points amplitude histogram was similar to that measured for the main state in 115 mM Ca²⁺ by SKM (Fig. 7).

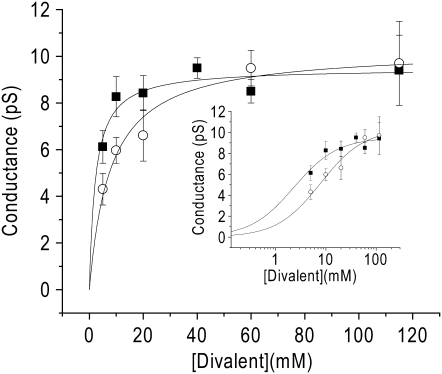
FIGURE 7.

Divalent ion concentration dependence of single-channel conductance. Slope conductance over a range of Ca²⁺ concentrations (squares, n = 19) and Ba²⁺ concentrations (circles, n = 26) (5–115 mM). All of the conductance measurements were made using all-points histograms except 115 mM Ca²⁺. Conductance was determined by the linear regression to the currents from multiple patches at each concentration. Data are displayed as the estimate ± SE. For each concentration, there were at least three patches with current amplitudes at three potentials, except in two cases: for 5 mM Ba²⁺, there was only one patch with three potentials and in 5 mM Ca²⁺ there were only two patches with three potentials. The data are fit with a Langmuir isotherm function. For Ca²⁺, γ_max = 9.5 ± 0.4 pS and K_M = 2.3 ± 0.7 mM. For Ba²⁺, γ_max = 10.3 ± 0.5 pS; K_M = 7.9 ± 1.3 mM. (Inset) The concentration dependence is displayed on a semilogarithmic scale.

When the main-state conductance was measured over a number of different divalent concentrations, the concentration dependence of unitary conductance for Ca²⁺ (squares) and Ba²⁺ (circles) were well fit with Langmuir isotherms (Fig. 7). Maximal conductance was not different for Ca²⁺ and Ba²⁺: γ_max was 9.5 ± 0.4 pS for Ca²⁺ and 10.3 ± 0.5 pS for Ba²⁺. The concentration for half-maximal conductance, however, was lower for Ca²⁺ (K_M = 2.3 ± 0.7 mM) than for Ba²⁺ (K_M = 7.9 ± 1.3 mM) (p < 0.01).

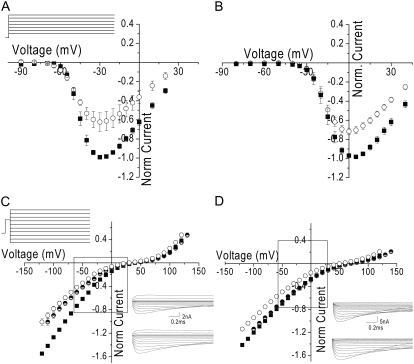
The ion dependence of single-channel conductance makes predictions about the relative size of the macroscopic current magnitudes as a function of Ca²⁺ and Ba²⁺ concentration. If we assume that this is a simple system, in which I_Ca = iNP_O, then we can predict that 1), at low divalent concentrations (<20 mM), the Ca²⁺ currents should be larger than the Ba²⁺ currents; and 2), at higher concentrations, the Ca²⁺ and Ba²⁺ currents should be equal. To test these predictions, we measured current-voltage relationships in the presence of 5 mM and 60 mM Ca²⁺ and Ba²⁺. For these experiments, we measured I_Ca and I_Ba in the same cell and varied the order in which the conditions were studied. As predicted from the 30% smaller Ba²⁺ conductance compared to Ca²⁺ conductance in 5 mM divalent in single channels, the macroscopic Ba²⁺ currents were smaller than the Ca²⁺ currents in 5 mM divalent (Fig. 8 A). However, in contrast to what was predicted by the single-channel conductance, the Ca²⁺ currents remained larger than the Ba²⁺ currents in 60 mM divalent (Fig. 8 B).

FIGURE 8.

(A) Whole-cell current-voltage relationship in the presence of 5 mM divalent (same as Fig. 1 B) and I/V voltage protocol (inset). (B) The whole-cell current-voltage relationship in the presence of 60 mM Ca²⁺ (solid squares) and Ba²⁺ (open circles). The data are displayed as mean ± SE normalized to the peak current in Ca²⁺. In the cases where the error bars are not visible, it is because they are smaller than the size of the symbol. For whole-cell experiments, the bath solution was the same as the single-channel pipette solution containing 60 mM Ca²⁺ and 60 mM Ba²⁺, respectively. (C) Average whole-cell open-channel I/V relationship in 5 mM Ca²⁺ (solid squares) and 5 mM Ba²⁺ (open circles) and voltage protocol (inset). The data are displayed as mean ± SE normalized to the current in Ca²⁺ at −80 mV. In the cases where the error bars are not visible, it is because they are smaller than the size of the symbol. The half-solid circles are the Ba²⁺ data shifted 10 mV positive (as described in text). Data were filtered at 100 kHz by an 8-pole low-pass Bessel filter and digitized at 200 kHz. Currents were recorded at hyperpolarized potentials after depolarization to +60 mV for 1 ms. (Inset) Capacity- and leak-corrected representative currents in 5 mM Ba²⁺ (upper) and Ca²⁺ (lower). Traces were filtered offline to 20 kHz and the first 0.05 ms are not shown. (D) Average whole-cell open-channel I/V relationship in 60 mM Ca²⁺ (solid squares) and 60 mM Ba²⁺ (open circles). The data are displayed as the mean ± SE normalized to the Ca²⁺ at −80 mV. In the cases where the error bars are not visible, it is because they are smaller than the size of the symbol. The half-solid circles are the Ba²⁺ data shifted by 20 mV (as described in text). Currents were recorded at hyperpolarized potentials after a brief depolarization to +115 mV for 1 ms. Data were filtered at 100 kHz by an 8-pole low-pass Bessel filter and digitized at 200 kHz. (Inset) Capacity- and leak-corrected representative currents in 60 mM Ba²⁺ (upper) and Ca²⁺ (lower). Traces were filtered offline to 20 kHz and the first 0.06 ms are not shown.

To investigate the cause of this apparent discrepancy between the whole-cell and single-channel data, we measured open-channel current-voltage relationships in each condition. Macroscopic conductance was determined over the voltage range between −120 mV and −60 mV, the same range over which we determined single-channel conductance. For the 5 mM divalent condition, the relative ratio of Ca²⁺ conductance to Ba²⁺ conductance was 1.43 ± 0.14, which is the same as the Ca²⁺/Ba²⁺ single-channel conductance relative ratio, 1.42 ± 0.28. For the 60 mM condition, macroscopic conductance in Ca²⁺ was similar to that in Ba²⁺, with a relative ratio of 1.10 ± 0.02. This was only slightly larger than predicted by the ratio of single-channel conductances, 0.9 ± 0.1.

Nonetheless, over the range of potential channels activated, I_Ca was larger than I_Ba under both divalent concentration conditions (Fig. 8, C and D). One of the assumptions in applying I = iNP_O is that both ions experienced the same driving force, i.e., reversal potential was the same. If reversal potentials for the two ions were different, it would contribute to differences in the relative size of the macroscopic currents. Visual inspection of the current-voltage relationships indeed indicated that there was a difference in apparent reversal potential for Ba²⁺ compared to Ca²⁺. The actual reversal potential is very difficult to evaluate in the current-voltage relationship because of the large flat region where inward divalent currents transition to outward monovalent currents. Therefore, to evaluate the extent to which this would affect the current-voltage relationship, we aligned open-channel I/Vs by shifting the Ba²⁺ data along the x axis to match current at the most positive potential. Because at the most positive voltages the outward monovalent currents were expected to be of the same magnitude in each condition (the intracellular monovalent cation was the same in each divalent condition), this “corrected” for the reversal potential difference. For the 5 mM divalent data this maneuver did not affect the relationship of I_Ca to I_Ba at negative potentials, but for the 60 mM data the currents aligned over the entire voltage range studied (Fig. 8, C and D, half-solid circles). This indicated that Ca²⁺ is much better at discouraging outward flux of K⁺ than is Ba²⁺, i.e., mixed divalent/monovalent flux is greater in the presence of Ba²⁺ than in the presence of Ca²⁺ and makes an important contribution to the differences in shape of the peak current-voltage relationship, especially at higher divalent concentrations. As a consequence of the voltage range over which they are determined, standard current-voltage measurements can give a misleading impression that there is a difference in conductance, when instead current magnitude is affected in an important way by the curvature in the relationship and the difference in apparent reversal potential under the two conditions (Fig. 8, C and D, boxes).

DISCUSSION

Early single-channel experiments in native cell types distinguished L-type Ca²⁺ channels from T-type Ca²⁺ channels by their differences in conductance in the presence of high concentrations of Ba²⁺; L-type Ca²⁺ channels displayed a higher conductance (∼3–5-fold) in high Ba²⁺ (∼110 mM) than T-type channels. For L-type channels, at least two studies have measured the single-channel conductance as a function of divalent concentration, and each found that maximal conductance for Ba²⁺ was ∼3-fold larger than that of Ca²⁺ (27,28). Although no previous studies have compared single-channel conductance as a function of both Ba²⁺ and Ca²⁺ concentrations for T-channels, the conductance for Ba²⁺ and Ca²⁺ has been measured in single high divalent concentrations (>90 mM) in native cells. All studies are consistent with the finding that the conductance is similar in Ca²⁺ and Ba²⁺, although values vary by 50%, ranging from 6 to 9 pS (1,8–11).

Single-channel measurements of recombinant channels expressed in heterologous systems are fewer, and no studies have directly compared the conductance in Ba²⁺ and Ca²⁺. The single-channel conductance for Ca_V3.1 expressed in Xenopus oocytes or HEK cells was reported as 7.5 pS in 115 mM Ba²⁺ measured over a voltage range of −10 to −50 mV (25) and 7.3 pS in 110 mM Ba²⁺ over a voltage range of −120 to 0 mV (21). In our hands, over a concentration range of 5–115 mM, γ_max was predicted from the fit to the conductance concentration data to plateau at 9.5 ± 0.4 pS for Ca²⁺ and 10.3 ± 0.5 pS for Ba²⁺, which was close to the conductance measured in 115 mM divalent, 9.4 ± 1.5 for Ca²⁺ and 9.7 ± 1.8 for Ba²⁺. The maximal conductance under our experimental conditions is higher than the previously reported conductance for heterologously expressed Ca_V3.1 in high Ba²⁺ concentrations but similar to some of the reports of conductance in native tissues. Discrepancies might reflect a difference in the voltage range over which conductance was measured in various studies, since the current-voltage relationship flattens at positive potentials. Here, we measured over a voltage range where there should be little if any contribution to conductance by outward monovalent flux.

Concentration dependence of single-channel conductance has been more extensively studied in native tissues. In chick and rat DRG cells, Carbone and Lux (1987b) measured the Ca²⁺ concentration dependence of single-channel conductance between 5 and 60 mM. They reported a γ_max of 5.7 pS with an apparent K_M of 10.3 mM. In this study, we measured a larger maximal conductance (9.5 pS) and a lower K_M (2.3 ± 0.7 mM). Although our data appear to differ from those of Carbone and Lux, this may be explained by several experimental differences between the two studies. The first and most likely explanation is the difference in the voltage range over which conductance was measured. Carbone and Lux measured conductance primarily over a voltage range of −60 to 0 mV, whereas our measurements were made over a more negative voltage range (−60 to −120 mV). If one compares γ at 20 mM Ca²⁺ determined over a voltage range similar to that of Carbone and Lux, our estimate of 4.2 pS (Fig. 4 C) is close to their reported value of 3.6 pS. In addition, Carbone and Lux studied native chick DRG cells using outside-out patches with intracellular Cs⁺. Here, we studied cloned Ca_V3.1 channels using cell-attached patches with intracellular K⁺. Cs⁺ is less permeant than K⁺ and would increase the rectification of the current-voltage relationship. Conductance measurements in native cells may also be complicated by the expression of multiple T-channel isoforms. Both Ca_V3.2 and Ca_V3.3 mRNA have been detected in rat DRG cells (29). Reported conductance values for Ca_V3.3, however, are higher than those for Ca_V3.1 (11 pS) (24) and the conductance reported for Ca_V3.2 is also variable, 5.3 pS (26) and 9.0 pS (30). Last, whereas the K_M measurement in single-channel studies by Carbone and Lux is higher than in our study, Carbone and Lux measured the K_M for macroscopic currents to be 5 mM, similar to our measurement of 2.3 mM (31).

An additional complication of measuring divalent conductance in T-channels is the presence of subconductance states. Several groups have anecdotally reported that T-channels open to subconductance states, both in native tissue (1,9,10) and in heterologous expression systems (24–26). Two studies in native cells and one study using heterologously expressed Ca_V3.3 have measured the amplitude of the subconductance state to be ∼50–60% of the main-state amplitude (1,9,24). The presence of subconductance states could potentially affect the measurement of current amplitude. Inclusion of subconductance states would be expected to broaden amplitude histograms and, depending on the signal/noise ratio, could cause the amplitude of the main state to be underestimated. Here, we report the presence of a subconductance state at ∼70% of the amplitude of the main conductance state in both 40 and 115 mM Ca²⁺. At 40 mM Ca²⁺, its presence did not interfere with amplitude measurements from histograms, but at 115 mM Ca²⁺, it did. This amplitude is slightly greater than that previously reported, although this may reflect the conditions under which it was measured (e.g., some of the studies measured the amplitude using a 1-kHz filter, which would be expected to somewhat attenuate the amplitude of a short-lived state), or it could be due to potential isoform differences. In addition, we observed an increase in the relative occupancy of the subconductance state in the presence of 115 mM Ca²⁺ compared to 40 mM Ca²⁺. Although subconductance states are biophysically very interesting, based on the subconductance state occupancy and amplitude measurements in 40 and 115 mM Ca²⁺, they would be predicted to produce only a 7% decrease in macroscopic conductance from 40 mM Ca²⁺ to 115 mM Ca²⁺. This is a rather small difference that would be difficult to measure under high divalent conditions, where voltage control is difficult to maintain and recordings are not sufficiently stable for >3–5 min. We were unable to reliably measure the amplitude of a subconductance state in Ba²⁺, although visual inspection suggested that one is present. It is either visited more rarely or the kinetics of the subconductance state are too fast to be reliably measured using a 2-kHz filter. These data suggest that there might be an ion dependence of the subconductance state occupancy and could prove to be helpful for determining the origin of these states. Tail-current protocols preclude a thorough analysis of the subconductance state kinetics, but the estimate of average lifetimes obtained using QuB indicated that the lifetime of the subconductance state is shorter than that of the main state, for which mean open time has been measured to be as short as 0.2–2 ms (1,2,9–11,14,32).

The data in this study agree with findings in the literature that the maximal conductance for Ca²⁺ and Ba²⁺ is similar (γ_max(Ca²⁺) = 9.5 ± 0.4 pS and γ_max(Ba²⁺) = 10.3 ± 0.5 pS). The apparent K_M, however, was 2.5-fold smaller in the presence of Ca²⁺ (2.3 ± 0.7 mM) than in the presence of Ba²⁺ (7.9 ± 1.3 mM), which was statistically significant (p < 0.01). The difference in apparent K_M suggests that at divalent concentrations similar to those used in whole-cell experiments, e.g., 2–20 mM, macroscopic Ca²⁺ conductance should be greater than Ba²⁺ conductance. In fact, if we observe the same voltage range over which the single-channel conductance was measured we find that at 5 mM divalent concentration, the macroscopic conductance for Ca²⁺ is larger than that for Ba²⁺. Furthermore, at 60-mM divalent concentrations, both the single-channel and whole-cell macroscopic conductances were similar for Ba²⁺ and Ca²⁺. Despite this, I_Ca > I_Ba at 60 mM. This reflects the difference in the ability of these two divalents to discourage outward permeation of K⁺, i.e., a difference in reversal potential, which makes the driving force for Ca²⁺ greater than that for Ba²⁺ in the range of potentials over which currents are typically measured. Ours is not the first report of this difference in selectivity; at least one group has previously noted differences in apparent reversal potential for Ca²⁺ and Ba²⁺ (12), although here we draw attention to its contribution to the I/V relationship relative to the contribution of single-channel conductance.

Other aspects of experimental conditions have also been reported to differentially affect Ca²⁺ and Ba²⁺ permeation, but were not explored here. In a study by Serrano et al. (12), it was reported that for Ca_V3.1 Ca²⁺ currents were larger than Ba²⁺ currents only in the presence of extracellular Mg²⁺, and these authors suggested that extracellular Mg²⁺ more strongly blocked Ba²⁺ currents than Ca²⁺ currents (12). Although they report no difference in Ca²⁺ and Ba²⁺ currents, they did see a similar difference in apparent reversal potential for the two conditions, with Ba²⁺ reversing 7 mV more negative than Ca²⁺. In addition to being blocked by extracellular Mg²⁺, T-channels are known to be blocked by protons in a voltage dependent manner. However, it is unclear whether the affinity of proton block is different for Ca²⁺ and Ba²⁺ currents. Our own preliminary experiments suggested that at pH 7.4 the contribution of proton block, if any, is small. However, one study demonstrated that for Ca_V3.1, the extent of proton block is reduced in the presence of increasing Ca²⁺ (33), suggesting that protons can produce open pore block in these channels and that the permeant ion affects the ability of protons to produce block. These or other properties might contribute to the similar, but not identical, Ca²⁺/Ba²⁺ conductance ratios we observed at 60 mM, 0.9 ± 0.1 predicted by γ and 1.1 ± 0.02 measured in open-channel I/V relationships.

Another factor that could affect the size of the macroscopic currents is the probability of opening under the two divalent conditions. We assumed in our analysis that probability of opening was similar under the conditions we compared. A difference in probability of opening in the presence of Ca²⁺ compared to Ba²⁺ was suggested by Shuba et al. (11), although the relative ratio of the macroscopic currents under the conditions of their study was 0.94, whereas this ratio for single-channel recordings was 0.67 (11). In a more recent study using whole-cell recordings, Shcheglovitov et al. (13) also suggested a difference in the probability of opening for Ca²⁺ compared to Ba²⁺. In our experiments, there was a very small difference in our conductance ratio measurements in the 60-mM divalent condition: the Ca²⁺/Ba²⁺ conductance ratio was 0.9 ± 0.1 for single-channel measurements compared to 1.1 ± 0.02 for whole-cell. It is conceivable that differences in probability of opening contributed to that remaining mismatch. In addition to differences in the probability of opening, differences in subconductance state behavior could affect the relative size of the macroscopic currents. Here, we found that the relative occupancy of the subconductance state was greater in 115 mM Ca²⁺ than in 40 mM Ca²⁺, although this is only predicted to decrease the macroscopic current ∼7%. We were unable to reliably measure subconductance activity in the presence of Ba²⁺ and therefore could not predict whether differences in subconductance state behavior between Ca²⁺ and Ba²⁺ could affect the relative size of the macroscopic conductance. A more extensive analysis of subconductance states is necessary to examine this possibility.

Although in this study we examined the Ca²⁺ and Ba²⁺ currents with an impermeant monovalent cation, TEA⁺, as the replacement cation, at least one group has found that the choice of the extracellular monovalent cation changes the apparent reversal potential, suggesting that there may be inward coflux of the monovalent cation with Ca²⁺ (34). These data are somewhat in contrast to those in a recent study in oocytes, which reported no significant shift in the apparent reversal potential when extracellular Na⁺ was replaced with TEA⁺ (13). Coflux of a monovalent cation would also be expected to significantly affect the size of both the macroscopic and single-channel currents. In addition to inward coflux with monovalents, backflux of the intracellular monovalent cation would be expected to affect the curvature of the current-voltage relationship and the potential range over which divalent flux predominates. The choice of intracellular monovalent cation, therefore, could also affect the measurement of single-channel conductance and the voltage range where it becomes nonlinear. Although our experiments did not directly measure the affinity of the divalent cation for the selectivity filter, one would expect that since the reversal potential is more negative in the presence of Ba²⁺, Ba²⁺ is less able to exclude monovalent efflux and therefore it can be predicted that Ba²⁺ block of monovalent permeation would be of lower affinity than Ca²⁺ block. Although the affinity of Ca²⁺ block of monovalent currents has been measured to be ∼1–2 μM both in native tissues and using heterologously expressed Ca_V3.1 (13,14,31), the affinity of Ca²⁺ has not been compared with that of Ba²⁺. In L-type calcium channels, Ca²⁺ block of monovalent currents has been measured to be ∼65- to 35-fold higher in affinity than Ba²⁺ block (35,36).

In summary, we have demonstrated that differences in both the apparent reversal potential and the K_M of single-channel conductance for Ca²⁺ and Ba²⁺ affect the relative size of the macroscopic currents. Measurements using a standard current-voltage relationship are particularly sensitive to differences in reversal potentials for the two divalent conditions. These experiments provide a platform for future studies to elucidate determinants of permeation in these versus other calcium-permeable channels.