Decision-making with multiple alternatives

Abstract

Simple perceptual tasks have laid the groundwork for understanding the neurobiology of decision making. Here, we challenge this foundation to explain how decision-making circuitry adjusts to a more difficult task. We measured behavioral and physiological responses on a 2- and 4-choice direction discrimination decision task. For both tasks, firing rates in the lateral intraparietal area appeared to reflect the accumulation of evidence for or against each choice. Evidence accumulation began at a lower firing rate for the 4-choice task, but reached a common level at the end of the decision process. The larger excursion suggests that subjects required more evidence before making a choice. Further, on both tasks, we observed a time-dependent rise in firing rates that may impose a deadline for deciding. These physiological observations constitute an effective strategy for handling increased task difficulty. The differences appear to explain subjects’ accuracy and reaction times.

Introduction

Organisms face decisions of varying complexity. In simple decisions, perceptual observations allow an animal to choose between action and inaction or between two alternative actions. These are simple instances of complex cognitive processes, which may require additional information from the environment or from memory. The ability to delay a response to consider incoming information is a hallmark of higher brain function.

Decisions between two choices in a perceptual motion task ^1–3 demonstrate mechanisms of decision making. In the task, humans or monkeys report the net direction of motion in a patch of moving random dots. In the reaction time (RT) version², subjects communicate their decision with a saccade when they are ready. This version identifies the period when subjects are accumulating evidence for a decision but have not yet committed to an alternative. How rapidly evidence accumulates depends on the strength of motion. The process ends when the evidence reaches a threshold or bound corresponding to one alternative. These “bounded accumulation of evidence” models encompass multiple mechanisms proposed to explain choice and decision time ^1,4,5

Several observations are consistent with the idea that evidence accumulates to a bound. First, a formal model of bounded accumulation accounts quantitatively for subjects’ speed and accuracy^3,6. Second, neuronal firing rates in the lateral intraparietal area (LIP) are consistent with evidence accumulation ^2,7–9. Specifically, when stimulus motion favors the target in the response field (RF) of an LIP neuron, firing rates build up progressively as monkeys form their decisions; the rate of buildup is proportional to motion strength. Finally, in the RT version, firing rates are similar at decision end when the monkey selects a target in the neuron’s RF, for all motion strengths and RTs. The stereotyped firing rate may reflect a bound that is common to easy and difficult motion strengths.

Because two-alternative choice tasks are simple, they may offer limited insight into decision making in general: organisms regularly face decisions among multiple alternatives. Here, we compare responses on a 4-choice decision-task with the 2-choice task. Our results argue that the bounded accumulation framework can be extended to explain more complex decisions, and they begin to reveal how decision-making circuitry adjusts to increasingly difficult decisions.

Results

Behavior

Two monkeys were trained on a 2-choice (Fig. 1a) and a 4-choice (Fig. 1b) motion discrimination task. We measured the accuracy and speed of their choices. In both tasks, accuracy was nearly perfect at high motion strengths and fell toward chance with lower motion strengths (Fig. 1d). The performance with strong motion reveals that the monkeys understood the relationship between stimulus direction and choice targets. Therefore, the more frequent errors at low motion strengths on the 4-choice task may be attributed to a failure to discriminate the direction of motion rather than confusion about action selection.

Figure 1.

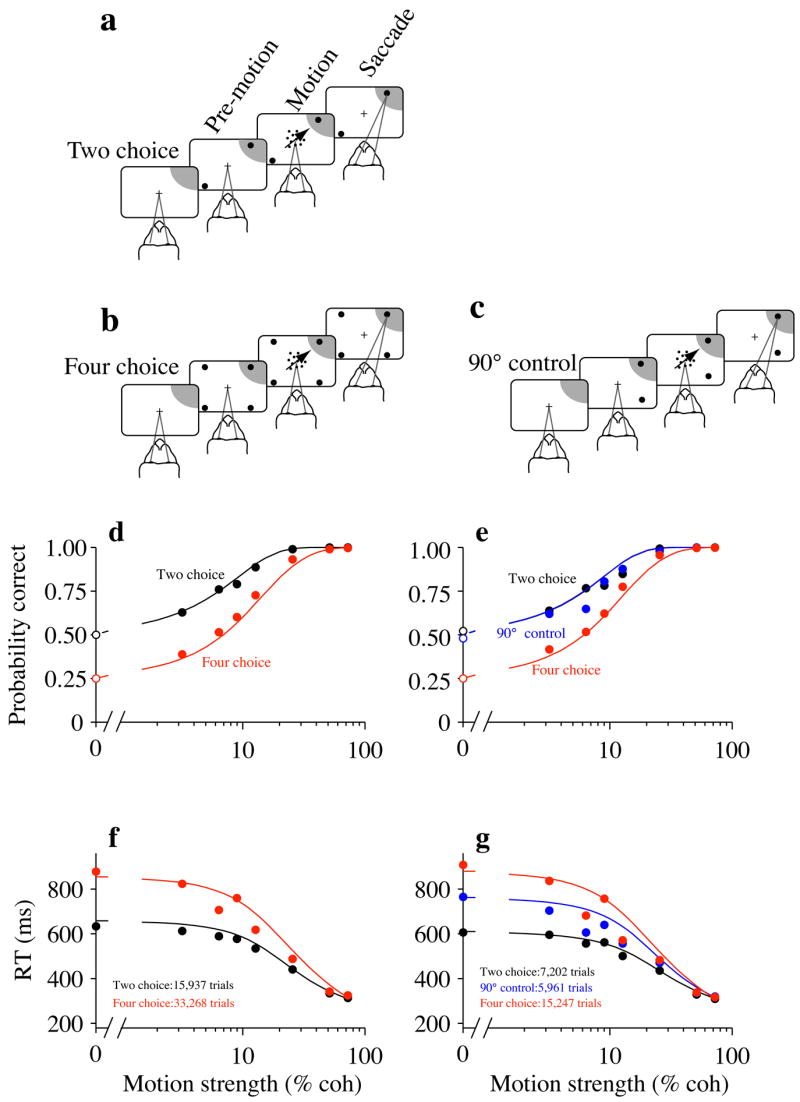
Task and performance, (a–c) Sequence of events on 2- and 4-choice direction discrimination tasks. The monkey fixates a central point until the random dot motion appears and is then permitted to indicate its decision by making a saccadic eye movement to a choice target. The motion is in one of 2 or 4 directions (trials randomly interleaved in a 1:2 ratio). A liquid reward is given for choosing the target along the axis of random dot motion, or it is given with probability ½ or ¼ when the motion strength is zero. Random intervals (truncated exponential distributions) separate fixation, appearance of choice targets and motion onset. The random-dot motion is extinguished when the monkey initiates a saccade to one of the choice targets. This interval, from motion onset to saccade initiation, is the RT. One of the choice targets is in the RF of an LIP neuron recorded during the task (shading). The shading is only meant as a guide: actual RF size varied considerably, (a) 2-choice task. The directions are 180° apart. One direction is toward the target in the neuron’s RF (T_in), (b) 4-choice task. The directions are 90° apart, (c) 90° control task, (d–g) Speed and accuracy of decisions. Smooth curves in all panels are fits to the bounded diffusion model described at the end of Results. The fits were performed separately for panels (d,f) and for panels (e,g). (d) Psychometric functions. The probability of a correct choice is plotted as a function of motion strength. All experiments contribute to these graphs. At 0% motion strength, choices are rewarded randomly (open symbols), (f) Psychometric functions for the 29 experiments that included the 90° control, (e) Chronometric functions. Mean RT for correct trials is plotted as a function of motion strength. Each point reflects correct responses from all experiments. Error bars are s.e.m.; some are smaller than the symbols, (g) Chronometric functions for the 29 experiments that included the 90° control.

Like accuracy, decision speed also depended on motion strength and the number of choices. RTs were longer on the 4-choice task¹⁰. These differences were largest at lower motion strengths but significant at all motion strengths (Fig. 1e, p<0.01).

We measured responses on an additional condition with 2 targets, 90° apart (Fig. 1c). This configuration (“90° control”) uses a subset of the targets and motion directions in the 4-choice task. Accuracy on this task emulated the standard 2-choice task (Fig. 1f), albeit with longer RTs, which fell between those on the standard 2- and 4-choice conditions (Fig. 1g).

Physiological responses on the 4-choice task

The 70 neurons recorded in our experiment had spatially selective persistent activity on delayed and memory-guided eye movement tasks (Supplementary Fig. 1). Multi- and single-unit responses with these characteristics are common in the ventral portion of LIP targeted in these experiments (LIPv ¹¹). In the motion discrimination task, one of the choice targets (T_in), was centered in the neuron’s RF. The other choice targets, (T_out and two orthogonal targets, T₉₀) were evenly spaced around a central fixation point (see Methods). On any one trial, for all but the 0% coherence stimulus, the motion was directed toward one target.

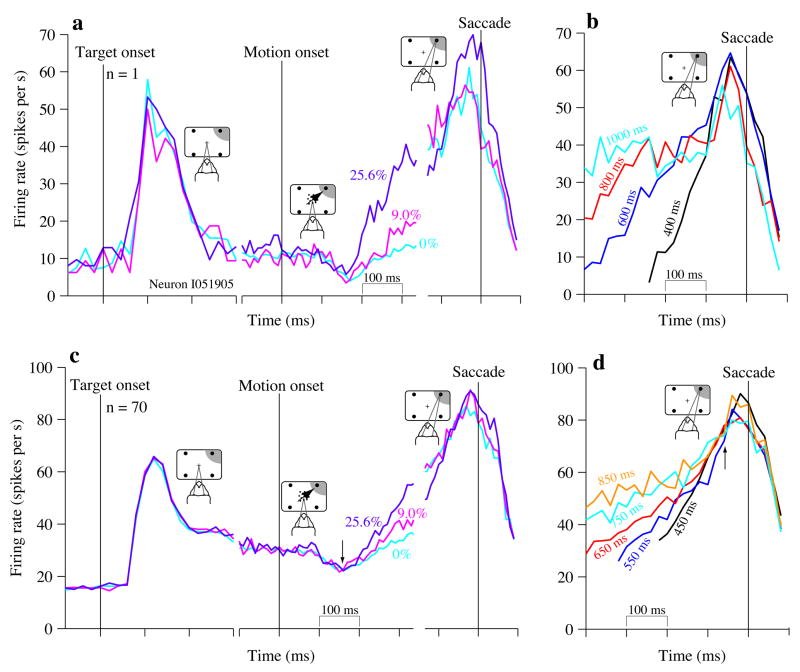
Target appearance caused a large, transient increase in firing rate (Fig. 2a,c, left) followed by the establishment of a baseline firing rate as the monkey awaited the onset of the random dot motion. Shortly after onset, the responses showed a brief dip (Fig. 2a,c, middle panel), followed by a gradual rise in firing rate. The dip, observed in other studies ^2,12–14, seems to mark the beginning of evidence accumulation. After the dip, the rate of increase in firing rate depended on motion strength (Fig. 2a,c middle). Near the saccade, however, this neural correlate of motion strength ^1,2,15 vanished (Fig. 2a,c, right). The stereotyped firing rate at the end of the decision is clearer when responses are grouped by RT (4 choice: Fig. 2b,d; 2 choice: Supplementary Fig. 2a) instead of motion strength. Analysis of variability across different RT groups provides quantitative support for a common firing rate close to the end of the trial (Supplementary Fig. 2b).

Figure 2.

Responses of LIP neurons on the 4-choice task are consistent with bounded accumulation. Firing rates are aligned to key events in the course of a trial, which are marked by vertical lines. For the trials depicted here, motion was either random (0% coherence) or in the T_in direction, (a) Average firing rates from 1 neuron. Left: responses aligned to onset of the choice targets; middle: responses aligned to the onset of stimulus motion; right: responses aligned to saccade initiation. For saccade-aligned responses, only T_in choices are shown. For purposes of display, traces are smoothed with a 30 ms exponential filter, (b) Responses reflect termination of the decision. Responses are grouped by RT at the values indicated (± 25 ms). The averages are aligned to saccade initiation and exclude neural activity within 200 ms of motion onset. Only correct T_in choices are included, and for clarity, every other RT group is not displayed. (c,d) Population average responses (N=70 neurons). Same conventions as in (a) and (b), except that no smoothing was performed; firing rates were computed in 20 ms non-overlapping bins. Arrow in (c) indicates the dip in firing rate seen shortly after motion onset. Arrow in (d) indicates the time when responses appear to coalesce, approximately 60 ms before the saccade.

This pattern of LIP activity in the 4-choice task is similar to the process underlying 2-choice decisions^1,2,16. The pattern is broadly consistent with a bounded accumulation of evidence among competing response mechanisms. Next we compared responses on 2- and 4-choice before the motion, during motion viewing, and just before the saccade to determine whether physiological differences on the two tasks can account for the behavioral differences we observed (Fig. 1).

Comparison of responses before motion

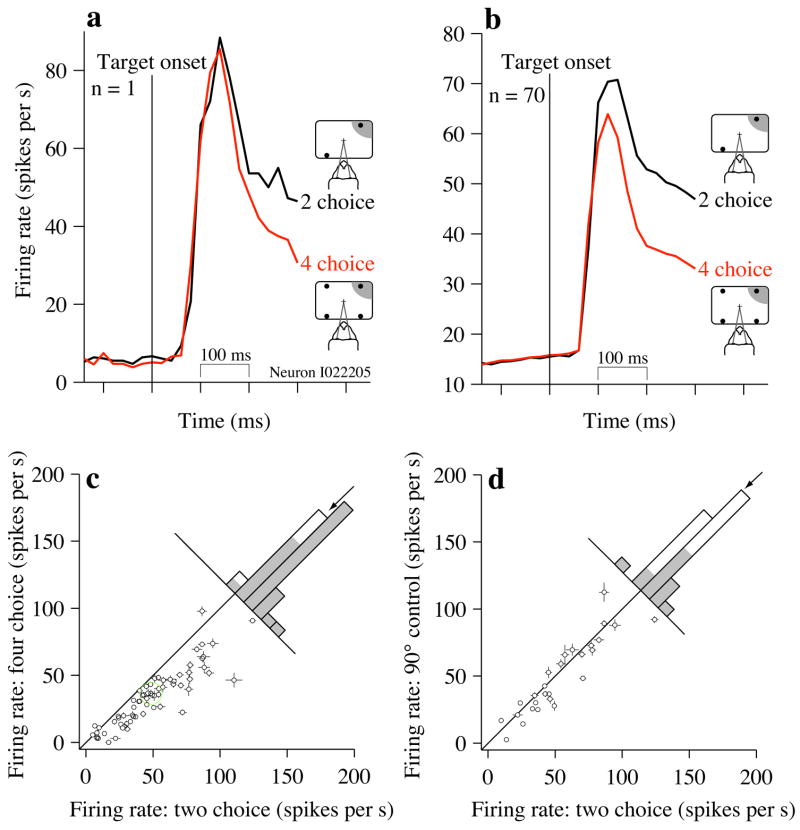
Responses before the stimulus reflect the state of decision-making circuitry before the monkeys begin accumulating evidence. Target appearance was the first cue indicating whether the ensuing discrimination would involve 2 or 4 directions. Between target appearance and motion onset, there was a clear difference in firing rates between 2- and 4-target conditions (Fig. 3). In the example (Fig. 3a), responses were 11.9±4.0 sp/s lower on 4-choice task (p<0.003). The reduced firing rate on the 4-choice task was evident across the population of neurons tested (Fig. 3b,c). It was subtly apparent in the transient target onset response and then was prominent until motion onset (mean difference = 16.1±1.6 sp/s, p<10⁻⁵, Fig. 3c, arrow). This effect was statistically significant in both monkeys (Monkey I: mean difference, 15.5±1.8 sp/s, p<10⁻⁵ Monkey S: 18.8±2.6sp/s, p<10⁻⁴).

Figure 3.

Neural responses in the pre-motion epoch are larger on the 2-choice task, (a) Average firing rate from a single neuron during the pre-motion epoch when 2 or 4 choice-targets were displayed. Vertical black line indicates the onset of the choice targets. Insets are a schematic of the target configurations used in this experiment. One target is in the neuron’s RF (shading). (b) Population average response. Same conventions as in (a) except that traces are average firing rates from 70 neurons. All trials contribute to these averages. Insets illustrate that one target is in the RF of the neuron; the location of this RF varies from neuron to neuron, (c) Comparison of firing rates from individual neurons on the 2- and 4-choice tasks. Responses were measured from 200 to 300 ms after choice target onset. The green circle marks the neuron shown in (a). Points for three neurons with high background firing rates are omitted from the plot to facilitate an appropriate scale for the remaining points (^{{227,174}, {132,99}, {144,127}}) Error bars are s.e.m. and are occasionally obscured by the points. Histogram displays the firing rate differences for all 70 neurons. Shading indicates significance (p<0.05). (d) Comparison of firing rates from individual neurons on the 2-choice and the 90° control tasks. Same conventions as in (c). Two neurons were omitted from the scatter plot ({131,138}, {227,226}).

Firing rate was also reduced in the 90° control task, though much less than in the 4-choice task (Fig. 3d, 3.7±2.1 sp/s lower on the 90° control task than on the 2-choice task, p<0.05). We conclude that the smaller angular separation between targets contributes to the reduction in activity seen in the 4-choice task in this epoch, but the reduction is largely explained by the number of choices.

Responses early in the motion epoch

The reduced firing rate on the 4-choice task persisted after motion onset. Recall that the motion is presented outside the neuron’s RF, and its earliest effect on LIP is a dip in firing rate (Fig. 2a). During this dip, firing rates were 9.17±1.05 sp/s lower for the 4-choice than for the 2-choice task (Supplementary Fig. 3, p<10⁻⁵). Thus this epoch retains much of the difference in firing rate seen before motion onset.

Following the dip, there was a time-dependent rise in the firing rate (“buildup”). The rate of this buildup offers insight into the conversion of sensory information into a decision variable, that is, the form of the evidence that underlies the choice and decision time. Four factors affect buildup: decision outcome, motion strength, number of choices present and the passage of time (Figures 4 and 5).

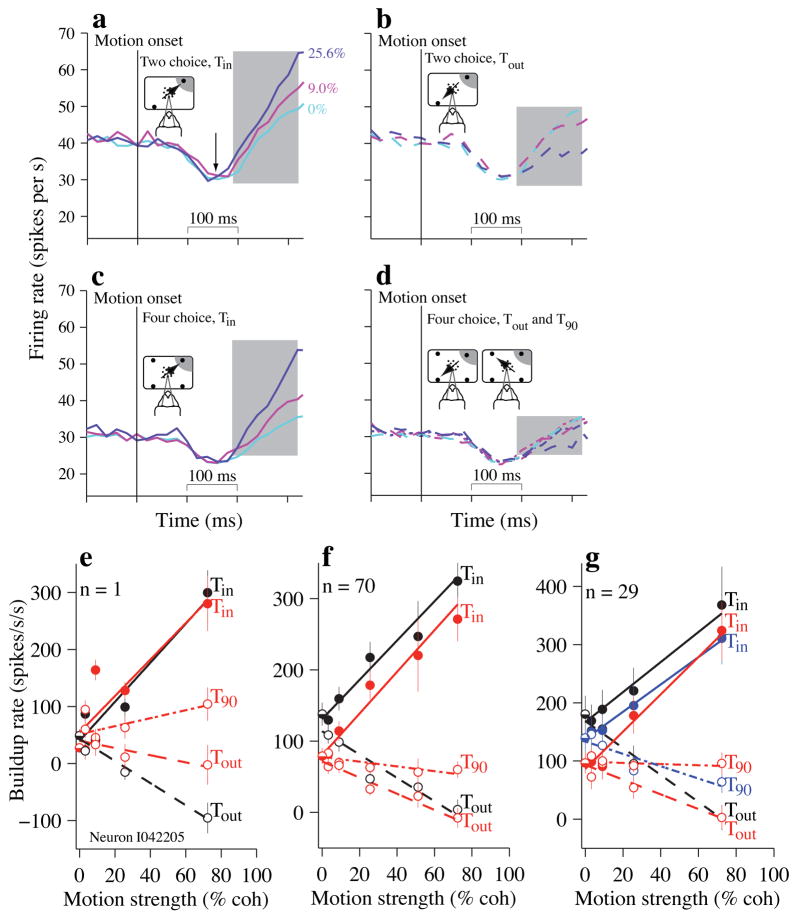
Figure 4.

Neural responses during motion viewing depend on difficulty, (a–d) Population average firing rates (N=70 neurons) are shown for three motion strengths. Panels group together trials based on the direction of motion and the number of choices (cartoon insets). Correct and incorrect trials are included in these averages. The traces for 0% coherent motion are identical in panels (a,b) and in panels (c,d). Only three motion strengths are shown for clarity. Shaded rectangle indicates the epoch used to estimate the buildup rates (190–320 ms after the onset of stimulus motion), (a) 2-choice trials when the motion direction was toward T_in. Arrow indicates the stereotyped firing rate “dip” that occurs after motion onset, (b) 2-choice trials when the motion direction was toward T_out. (c) 4-choice trials when the motion direction was toward T_in. (d) 4-choice trials when the motion direction was toward T_out (dashed line) or toward an orthogonally positioned (T₉₀) target (dot-dash line). The five traces on this panel are largely superimposed. The single cyan trace is for 0% coherent motion averaged across all choices (T_in, T_out and T₉₀; same as cyan trace in c) (e–g) Effect of motion strength on buildup rates, (e) Single neuron example. Buildup rates were estimated for each motion strength; these buildup rates (±s.e.) are plotted as a function of motion strength. The slope of the fitted line estimates the effect of a unit change in motion strength on the buildup rate. Black, 2-choice; Red, 4-choice. 5 motion strengths were tested for this neuron (methods) (f) Same conventions as in (e) except that buildup rates were calculated in individual neurons and then averaged across the population (N=70 neurons) before fitting the line. Error bars are s.e. of buildup rates across neurons, (g) Population analysis for the 29 neurons tested with the 90° control condition in addition to 2- and 4-choice trials. Blue lines correspond to the 90° control condition; error bars are s.e. of buildup rates across neurons. Points corresponding to 51.2% motion strength are not included on this plot because this motion strength was tested in only 3 neurons.

Figure 5.

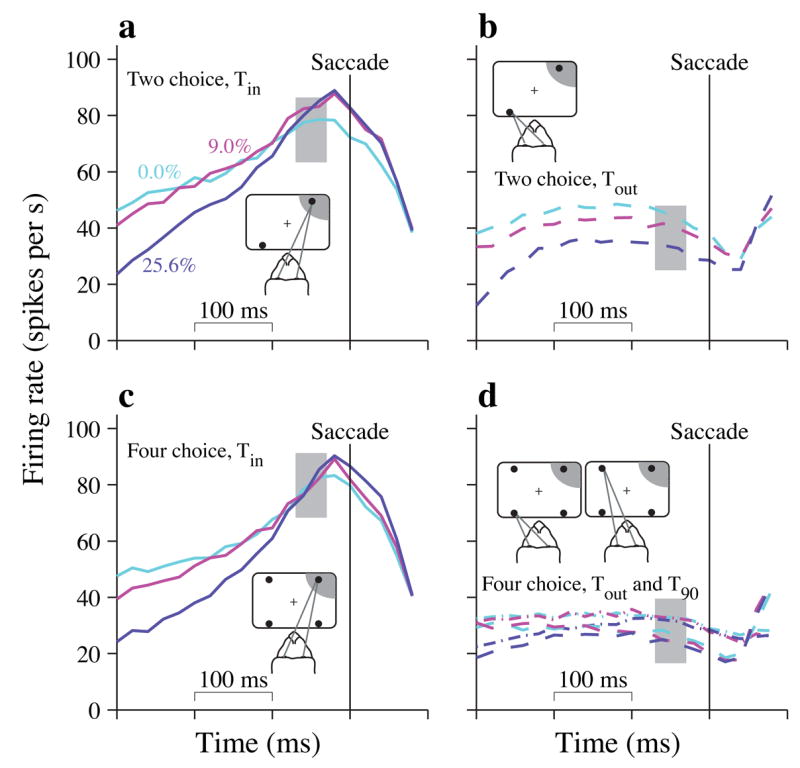
Neural responses just preceding the eye movement responses. Population average firing rates (N=70 neurons) are shown aligned to the initiation of saccades (vertical line). Panels group together trials based on the direction of the saccade with respect to the RF of the neuron (cartoon insets). Only 3 motion strengths are shown for clarity, (a) T_in choices in the 2-choice task, (b) T_out choices in the 2-choice task, (c) T_in choices in the 4-choice task, (d) T_out (dashed) and T₉₀ (dot-dash) choices in the 4-choice task.

The effect of choice is most conspicuous late in the decision process (Fig. 5a–d). Our sample was screened for spatially selective responses on delayed eye-movement task, so all neurons are expected to indicate the decision outcome. What interests us is the change in firing rate accompanying decision formation. Early on, decision outcome has only a weak effect on the neural responses. We therefore analyzed groups of trials with the same motion strength and direction, regardless of the monkey’s eventual choice (our conclusions also hold if trials are grouped by motion strength and choice; Supplementary Fig. 4).

To quantify how sensory information is converted into decision evidence, we estimated firing rate buildup at each motion strength (Fig. 4a–d, buildup rate = slope of a line fit to the shaded portion of the response). Buildup rates scale approximately linearly as a function of motion strength for motion toward and away from the neuron’s RF. This relationship was similar on 2- and 4-choice tasks. For motion toward T_in, these slopes differed by only 0.17±0.45 sp.s^−2.%coh⁻¹ (Fig. 4f, p=0.71, parallel solid lines). For motion toward T_out, increasing motion strength suppressed buildup rate slightly more in the 2-choice condition, but the difference was not reliable (difference = 0.50±0.31 sp.s^−2.%coh⁻¹; p=0.11, see Methods, Eq. 3). These trends were also apparent in single neurons (Supplementary Fig. 5a,b). We conclude that LIP registers evidence along the T_in–T_out axis similarly for 2- and 4-choice tasks. Thus, differences in behavior are not explained by differences in the mapping of motion information onto a change in LIP firing rate.

This analysis also suggests that LIP is only weakly affected by motion in directions orthogonal to the T_in–T_out axis on the 4-choice task. Stronger motion reduced the firing rate slightly (Fig. 4f, slope of red dot-dash trace = −0.33±0.09 sp.s^−2.%coh⁻¹, p<10⁻³). Although in any one experiment, either T₉₀ direction might provide weak positive evidence for a T_in choice (e.g., Fig. 4e), the net effect of orthogonal motion is weak negative evidence, on average.

A prominent buildup in firing rate does not depend on motion strength or direction and is not explained by the monkey’s choice, as seen in 0% motion strength trials, which favor all directions equally, on average (Fig. 4a–d, cyan traces). Although the monkeys distributed their choices with nearly equal frequency to all (two or four) choice targets, firing rates increased as a function of time. The rate of this buildup is the y-intercept of each line in Figures 4e and f. It is considerably larger for 2- than for 4-choice (Figure 4f 2-choice intercept 50.7±8.2 sp/s/s greater than 4-choice intercept, p<10⁻⁵, also see Discussion & Supplementary Fig. 6b,c). This time-dependent rise is not explained by random fluctuations in motion energy because the increase was evident when trials ending in T_in and T_out choices were averaged together (as in Fig. 4a–d). We interpret this rise as a reflection of the cost associated with the passage of time, corresponding to the psychological sense of urgency, u(t) ^17,18. The positive buildup rates at all motion strengths and for all directions effectively impose a deadline on the decision process—a deadline that is earlier when there are just 2 choices.

The 90°-control task (N=29) allows us to ascertain whether the differences in LIP responses on the 2- and 4-choice tasks are explained by differences in number of choices per se or the difference in angle between motion directions. Recall that before motion onset, activity on the 90°-control trials was slightly reduced in comparison with the standard 2-choice task. This reduction became more modest through the “dip” during the beginning of motion (2-choice responses were 2.66±2.0 sp/s higher than 90° responses, p=0.10), followed by a buildup in firing rates leading to the decision.

The effect of motion strength on these buildup rates was similar to 2-choice responses for motion toward T_in (Figure 4g; for the population, slopes differed by 0.23±0.32 sp.s^−2.% coh⁻¹, p=0.47). However, for motion toward T₉₀, a 1% increase in motion strength decreased buildup rate. This suggests that motion toward T₉₀ constitutes weak evidence against the T_in choice. It raises the possibility that the near absence of an effect of orthogonal motion on the 4-choice task is an artifact that results from averaging the two orthogonal directions. Alternatively, the T₉₀ direction may be more likely to contribute negatively to T_in choices without a T_out alternative.

As before, some of the buildup in firing rate on the 90°-control task is not attributed to an accumulation of motion evidence, because it is present even on trials with 0% motion strength. The magnitude of this urgency signal, u(t), fell between those measured on the 2- and 4-choice tasks (Table 1; Supplementary Fig. 6c).

Responses late in the motion epoch

On a variety of 2-choice decision tasks, a threshold crossing is associated with termination of the decision ^1,2,19. We see evidence for a threshold on the 4-choice task as well (Fig. 2d). We now ask whether this threshold differs for 2- and 4-choice tasks.

Firing rates just preceding T_in choices were similar for 2- and 4-choice trials (Fig. 5a,c; responses in shaded region were on average only 3.1±1.3 sp/s higher for 4-choice than for 2-choice, p<0.03). Although significant, this difference amounts to only 3.7% of the firing rate in this epoch. Further, unlike the buildup rates at the beginning of the decision, the firing rates at the end of decisions for T_in did not vary as a function of motion strength (p>0.57 for 2 and 4-choice) and were the same for correct and error trials (p>0.78 for 2- and 4-choice). We conclude that the termination of decisions is associated with a fixed firing rate when the monkey chooses the target in the RF.

We are less certain about the characterization of firing rates just preceding T_out and T₉₀ choices. Firing rates tended to be lower on the 4-choice task overall (difference = 9.81±4.08 sp/s, p<0.02). Because firing rates were already lower at the beginning of these trials, the persistence of this difference is only remarkable in contrast with the T_in choices. What remains unclear is whether the firing rates achieve a stereotyped level before the saccade or whether they reflect the motion strength and RT. We observed a weak dependence of firing rate on motion strength, but the effects were not statistically reliable (p>0.07 in all cases). In the context of bounded accumulation, a weak relationship between motion strength and firing rate raises the possibility that the losing decision process (or processes) convey information about the degree of difficulty²⁰.

Firing rate excursion

Firing rates at the beginning and end of the motion-viewing period suggest that LIP neurons undergo a larger change in firing rate during decisions among 4 possible alternatives. When choices were to the target in the neuron’s RF, firing rates for the 2- and 4-choice task ultimately reached a similar value near the time of the saccade (Fig. 2d, Supplementary Fig. 2a). However, the initial response when the motion began was lower for the 4-choice task than the 2-choice task (Fig. 3). We confirmed this by estimating the “firing rate excursion” from each neuron (Fig. 6).

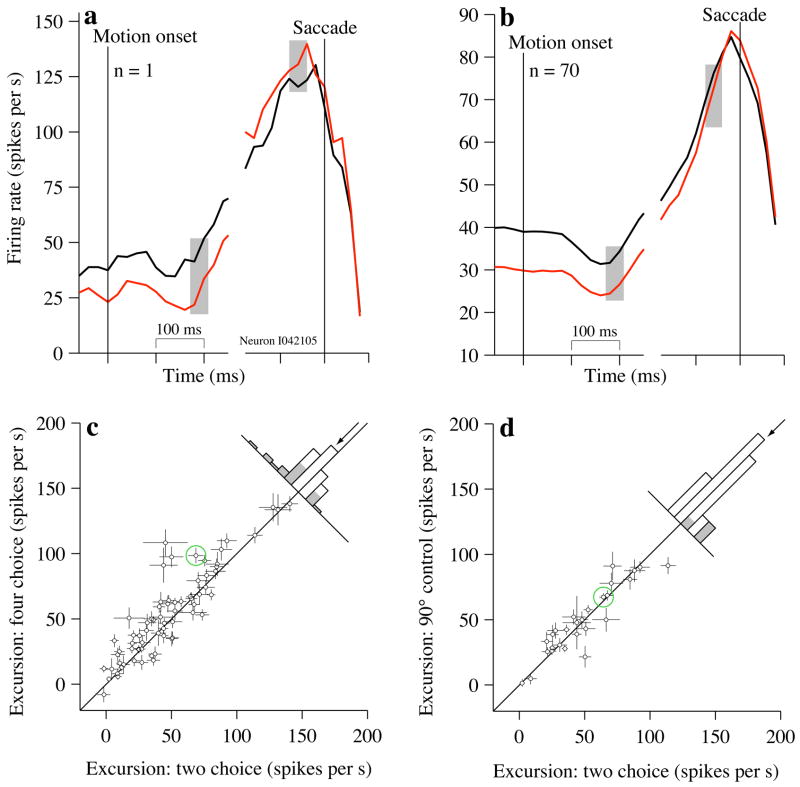
Figure 6.

Firing rate excursion is larger on the 4-choice task, (a) Firing rates on 2- and 4-choice trials at the beginning and end of the motion-viewing period for a single example neuron. Responses are aligned to motion onset (left) and saccade initiation (right). Black and red traces indicate responses on the 2- and 4-choice tasks, respectively. For purposes of display, traces are smoothed with a 30 ms exponential filter. Excursion is the difference between firing rates in the shaded regions. All responses leading to correct T_in choices and with RT>450 ms are used in this analysis. Firing rate excursion was 29.7±8.4 sp/s larger for 4-choice than for 2-choice. (b) Same as (a) except that traces reflect the average firing rate from 70 neurons and no smoothing was performed; firing rates were computed in 20 ms nonoverlapping bins, (c) Comparison of firing rate excursion on 2- and 4-choice tasks. Points are estimates of the firing rate excursion from single neurons. One point {170,159} was omitted from the scatter plot to facilitate scaling of the remaining points. Error bars show s.e. of the excursion (Eq. 2) and are occasionally obscured by the points. Green circle marks the example neuron in (a). Histogram depicts the differences in excursion on 2- minus 4-choice tasks. Arrow indicates the mean. Only correct responses to T_in targets were used for this analysis. Gray shading indicates individual neurons with significant differences (p<0.05). (d) Comparison of firing rate excursion on 2-choice and 90°-control tasks. Same conventions as in (b). The same neuron {170,157} was omitted from the scatter plot.

The difference in firing rates at the beginning and end of motion-viewing combined to make a total difference in firing rate excursion of 6.11±0.21 sp/s larger for 4-choice than for 2-choice (see Methods, Eq. 2). This difference, present in individual neurons (e.g., Fig. 6a), was highly significant across the population (Fig. 6b,c, p<0.0005) and in both monkeys individually (excursion difference: Monkey I: 4.7±0.27 sp/s, p<0.02, Monkey S: 11.9±1.0 sp/s, p<0.005). The magnitude of this difference depends on which interval we use to estimate firing rates at the end of the trial, but the effect is statistically significant for a wide range (Supplementary Fig 2c). These estimates were obtained using only correct trials, but we obtained a similar estimate when we included all the trials made to the T_in target.

The difference in excursion is attributed to the number of choices. The firing rate excursion on the 90° control task was nearly identical to that seen on the standard 2-choice task (Fig. 6d; mean difference 0.13±0.37 sp/s, p=0.53). The change in excursion in the 4-choice task was also confirmed in this subset of neurons (mean difference 4.2±2.3 sp/s larger for 4-choice than for 2-choice, p<0.04). Thus, the angular separation between choice targets alone is, by itself, insufficient to cause an increase in firing rate excursion of the magnitude seen on the 4-choice task.

Relationship between LIP activity and behavior

The preceding analyses expose the similarities and differences in how LIP activity reflects a bounded accumulation of evidence during 2 and 4 choice decisions. We next attempt to relate these observations to behavioral measurements of choice and RT. We have already noted that firing rates build up faster in association with strong motion and fast RT. Moreover this buildup begins at a fixed time after the onset of motion and signals the end of decision (for T_in) by achieving a critical level. Here we provide two additional analyses in support of this mechanism.

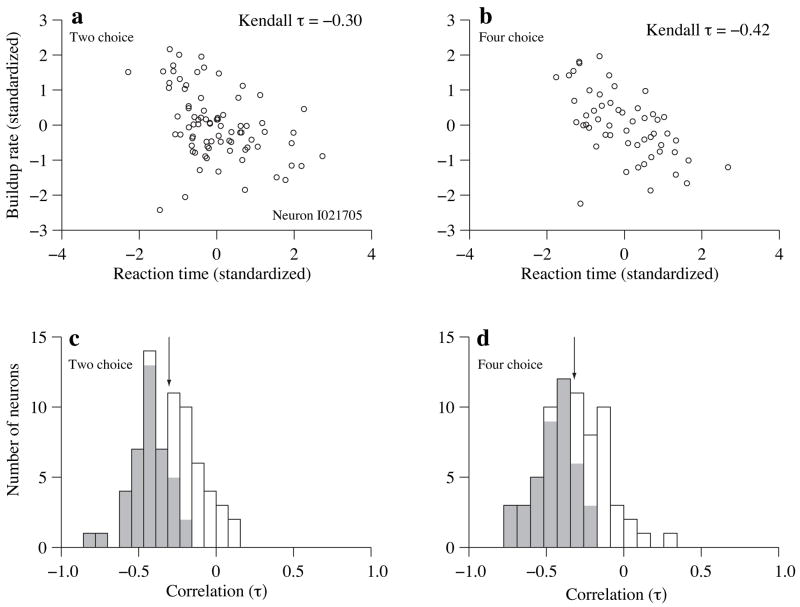
First, we examined the relationship between buildup rate and RT for single trials that terminated with a T_in choice (Fig. 7). For each neuron, the single-trial estimates of buildup rate and the measured RT were detrended to remove the effect of motion strength (see Methods) and combined in a scatter plot (Fig. 7a,b). Trial-to-trial variability in buildup rate was inversely correlated with trial-to-trial variability in RT, despite the noisy estimate of buildup rate and large variation in RT. This observation was typical of the data (Fig. 7c,d; 2-choice: mean correlation coefficient was −0.22±0.02, p<10⁻⁵, N=70 neurons; 4-choice: mean correlation coefficient was −0.26±0.02, p<10⁻⁵, N=69).

Figure 7.

Neural responses and RTs are inversely correlated on single trials, (a) Trial-by-trial correlation between RT and buildup rate for one representative neuron (Kendall τ=−0.30, p<10⁻⁴). Values are expressed in units of standard deviations from mean. This detrending was performed for each motion strength using all correct T_in choices and all T_in choices for 0% coherence, (b) Same as (a) but for 4-choice trials (τ=−0.42, p<10⁻⁴). (c–d) Distribution of correlation coefficients (Kendall τ) for each neuron in the data set. Gray shading indicates individual neurons with significant correlation (p<0.05). (c) 2-choice task. Arrow indicates the mean, (d) 4-choice task. Arrow indicates the mean.

Next, we attempt to reconcile LIP activity on the tasks with speed and accuracy (Fig. 1d–g). The excursion of LIP firing rates throughout the decision is larger on the 4-choice task (Fig. 6). The change in LIP buildup rates produced by a change in motion strength toward T_in is similar for 2- and 4-choice tasks (Fig. 4). The rise in firing rate that depends on time but not on motion strength or direction (u(t), urgency) is larger in the 2-choice task (Supplementary Fig. 6b, c). All these observations are consistent with longer RTs on the 4-choice task: it takes longer for LIP firing rates to undergo the larger excursion. These observations have less intuitive effects on accuracy. For example, the larger excursion and less pronounced time-varying increase would lead to better accuracy on the 4-choice task, were it not for the larger number of choices.

Our model implements a race between 2- or 4-choice mechanisms to determine which target will be selected (Supplementary Fig. 6a, d). Each mechanism accumulates momentary evidence in favor of the choice target in its RF. A decision ensues when one of the accumulators reaches a bound. We used the physiology to constrain bound height and u(t). Three additional parameters were adjusted to fit the choice and RT data (see Methods and Table 1). We are cautious about interpreting the values of the fitted parameters since we have fixed the most important model parameters using the LIP measurements. The important point is that they are reasonably similar for the 2- and 4-choice tasks.

The model provides an adequate account of both RT and accuracy on both tasks (smooth curves Figure 1,d–g). This fit supports the hypothesis that the framework of bounded accumulation can be extended to explain decisions with more than 2 alternatives. Moreover, the physiological differences on the 2- and 4-choice tasks are of the right size to explain the behavioral differences we observed. The model also accounts for the longer RTs observed on error trials for both the 2- and 4-choice task (Supplementary Fig. 7). This model—especially the hybrid of fixed and free terms—is not unique but underscores the consistency of physiological and behavioral measurements within the framework of bounded accumulation.

Discussion

Simple experimental models that build on knowledge about sensory and motor functions (reviewed in¹) have the downside that they rely on mechanisms that may be inadequate for more complex decisions. Relative to 2-choice decisions^2,8,9,21, our 4-choice task doubles the number of alternatives and halves the angular separation between directions. Although this angle remains large compared to fine discriminations that humans and monkeys can make ^22–24, it did increase difficulty slightly, as shown by 90° separation in a 2-choice task. Longer viewing durations were required for the same accuracy (Fig. 1f, g).

To achieve an acceptable reward rate, we used a mixture of motion strengths that favored easier conditions, compared to previous choice-RT experiments (e.g., ²). The set was identical in all conditions, so the 2-choice task was easy, probably explaining the faster RTs here. The monkeys could afford to terminate choices using a more lax criterion — what we interpret as a shorter excursion to a termination bound—without increasing the average probability of error.

Many models are proposed to explain the coordination of RT and choice accuracy in 2-choice tasks ^4,18,25–27. These models share a common feature: a termination bound is applied to some form of evidence representation, the decision variable. A putative neural correlate of this operation is evident in area LIP: for all RTs (and motion strengths), the firing rates of LIP neurons reach a stereotyped level shortly before the monkey initiates a saccade to indicate its choice for T_in (Fig. 2b, d and Supplementary Fig 2a, b). Our findings suggest that this same bounded accumulation framework applies to decisions among 4 choices. This hypothesis was suggested by theorists^5,28,29 but had not been tested.

A major difference between 2- and 4-choice responses was the firing rate at the beginning of the decision process (Fig. 3), consistent with the inverse relationship between the number of possible eye movement directions and firing rates in the superior colliculus preceding a saccade instruction ³⁰. We think the reduction in firing rate on 4-choice is unlikely to be due to a low-level factor, such as the presence of a target in the neuron’s inhibitory surround. This possibility was refuted in the superior colliculus by dissociating uncertainty from the number of targets. We tried to place the monkey in a 2-choice task while providing 4 targets (two irrelevant), but this manipulation introduced unacceptable biases in subsequent testing. Nonetheless, we doubt that surround suppression explains the observed firing rate reduction. First, no inhibitory surround is seen in LIP RFs ^31,32. Second, responses to the T₉₀ target on our screening saccade task were not lower than responses to the T_out target, as would be expected if they were in an inhibitory surround (Supplementary Fig. 1c). Third, in two experiments, we observed a reduction in firing rate on the 4-choice task even when RFs were large enough to encompass the orthogonal targets in their excitatory regions (data not shown).

In our 4-choice task, this lower firing rate at the decision’s beginning confers a higher bound for terminating the decision. Three experimental findings support this conclusion. First, the firing rate at the decision’s end is similar in the 2- and 4-choice configurations. Thus the lower starting point implies a larger excursion in firing rate from start to end of the decision. Second, the rate of buildup in LIP that can be attributed to motion strength was similar on 2- and 4-choice configurations for motion toward T_in (Fig. 4) and for T_in choices (Supplementary Fig. 4). This rules out the possibility that the difference in excursion was compensated by a change in the scaling of accumulated evidence into units of LIP firing rate. Third, the urgency, u(t), was stronger in 2- than 4-choice conditions. This amplifies the effective difference in excursion between the conditions because it effectively shrinks the excursion: less of the range of LIP firing rates between start and end is used to represent the accumulated evidence.

In the framework of bounded accumulation, a larger excursion improves signal to noise at decision termination—or equivalently, reduces uncertainty—at the expense of decision time. When human subjects perform the 2-choice motion task, they appear to adjust the bound (or excursion) when they trade off speed and accuracy³. When the number of alternatives is increased, all else being equal, the level of uncertainty is initially increased. Thus, it is not surprising that the brain would accrue more evidence before terminating the decision. The cost is decision time, but this is tempered by implementation of a deadline imposed by the urgency signal.

We identified this urgency signal as the time-dependent rise in firing rate that is seen on all trials regardless of motion strength and direction. For example, when the evidence is neutral (0% coherence), assuming no choice bias, the bounded accumulation model approximates an unbiased diffusion of evidence: a rising variance but no change in the mean evidence. The urgency signal is the difference between the observed firing rates and this expectation from unbiased diffusion. It is an essential feature of the model used to explain choice and RT in these experiments. A time-dependent rise of firing rate in LIP and elsewhere has been interpreted as a representation of elapsed time in the form of a hazard rate or anticipation function ^12,33–35. in the framework of bounded accumulation ¹⁷, it causes decisions to terminate as time elapses, regardless of the evidence.

In the 4-choice task, time is costly. Long decision times would improve performance above chance (25% correct), but not for the 0% motion strength trials and not by much for the next weakest motion strength. It is therefore sensible to place time limits on the decision process. Similar reasoning applies to the 2-choice configuration. Because chance represents 50% correct, there is less impetus to complete the trial at weak motion strengths, which probably explains the weaker urgency signal, u(t), seen previously in 2-choice experiments^2,36. Here, however, our easy set of motion strengths rendered fast decisions less costly in the 2-choice task.

A remaining question is how signals from direction-selective neurons in the middle temporal area (MT) are combined into momentary evidence. In the two-choice task, LIP neurons seem to reflect the difference in firing rates between neurons tuned to two opposing directions of motion²¹. This oppositional relationship was demonstrated directly by stimulating MT neurons and measuring the effect on choice and RT. Buildup rates in LIP reflect, at least in part, this subtraction: a change in motion strength in the direction favoring T_in leads to a proportional rise in buildup rate in LIP, and an opposite change in motion strength leads to a comparable decline. Our results suggest that the computation that LIP performs on the motion signals it receives from MT (and elsewhere) is similar in the 2- and 4-choice tasks. In the latter, the contribution of the two non-opposing directions (T₉₀) was small (figure 4f, red dot-dash trace), but we doubt this will generalize to more directions and choices. Our experiment is not definitive here, in part because the angle between alternatives is large compared to the range of angles that primates can discriminate ^22–24.

Our study suggests that some of the principles gleaned from simple binary decisions are likely to extend to decisions with more than 2 choices. Specifically, we observed a neural correlate of evidence accumulation in structures that represent the choice. In addition, the observed bound on the accumulation ties together in a single mechanism the content of a decision with the time required to make it. It remains to be seen whether the framework will extend to decisions among more than 4 choices ^28,37,38 or to decisions among a continuous array of choices, in which a parameter can take on any value, like the heading of a compass ³⁹. It may seem that, according to the bounded accumulation framework, decisions among continuous choices would require an infinite number of accumulators. This framework may simply not be able to account for decisions among continuous choices and may need to be replaced with a more suitable model^27,40. Alternatively, decisions among continuous choices might be explainable using a finite number of accumulators. The resolution of cognitive and motor systems may not require that the brain represent an infinite array of possibilities with precision; the degree of uncertainty reduction need not exceed that of the systems that use the estimate. If so, a bounded accumulation framework with a finite number of accumulators may be sufficient, even for decisions among continuous choices.

Methods

Behavioral tasks

Stimuli were shown on a CRT monitor (refresh rate: 99Hz) positioned 59 cm from the monkeys. Stimuli were generated using Matlab 5.2 (Mathworks, Natick, MA) and the Psychophysics toolbox ^41,42.

For the random dot motion task, trials were similar to those reported elsewhere ^2,8,36 (Fig. 1a–c). Following successful fixation (± 1.5°) of a central white target, two or four highly visible, red peripheral choice targets appeared (diameter =0.5°). Choice targets were 180° apart (2-choice task) or 90° apart (4-choice task and 90° control task). All choice targets were equally eccentric (range = 4–15°; mean 10.5°). 2- and 4-choice trials were randomly interleaved. The dynamic random dots were displayed in a 5° circular aperture centered on the fixation point. We used a variable coherence random dot display^2,8,43 (dot density = 16.7 dots/deg²/s). Coherently moving dots were displaced to produce 6°/s motion. For the first 20 neurons examined, 6 motion strengths were used: (0%, 3.2%, 6.4%, 25.6%, 51.2% and 76.8%). For the remaining 50 neurons, only 5 motion strengths (0%, 3.2%, 9.0%, 25.6% and 72.4%) were used so as to maximize the number of trials/condition collected. For graphs, combined data from the highest motion strengths are shown at 72.4% coherence.

The motion stimulus was extinguished when the monkey’s gaze exited the fixation window. Saccades ending in a window (range: ±1.5° to ±3.5° depending on eccentricity) around the choice target corresponding to the correct direction of stimulus motion were rewarded with juice or water. Otherwise, no reward was given, and the correct choice target briefly doubled in size to provide feedback. For Monkey S, a delay of 1000 ms was imposed after incorrect trials before the next trial began to discourage fast choices.

Two additional tasks were used: overlap and memory saccades. In the overlap saccade task, a peripheral target was placed in the visual field while the monkeys maintained fixation of a central spot during a delay period. The delay period was random, sampled from a truncated exponential distribution. When the central spot was extinguished, the monkeys made a saccade to the choice target. In the memory saccade task, the peripheral target was flashed only briefly; the monkeys made a saccade to its remembered location. Memory and overlap saccade tasks were performed before the discrimination task to verify the spatial selectivity of the neuron; trials using the overlap saccade task were usually randomly interleaved with motion discrimination trials to test for stability of the RF and the neural responses (Supplementary Fig. 1a, b).

Electrophysiology

Two monkeys (I, 51 neurons; S, 19 neurons) were prepared for chronic single neuron recording using standard surgical procedures^2,8. All surgical and experimental procedures were in accordance with the NIH Guide for the Care and Use of Laboratory Animals and were approved by the University of Washington Animal Care Committee.

Electrodes (Alpha Omega, Alpharetta GA) were introduced into area LIP at each daily recording session. Neural responses were amplified conventionally, and waveforms corresponding to different neurons were sorted online using the Plexon Sort Client (Plexon Inc, Dallas TX). The Plexon Offline Sorter was used after each experiment to confirm that all recorded spikes came from single well-isolated neurons, based on waveform shape and a refractory period.

Neurons were selected according to anatomical and physiological criteria. Anatomical landmarks were provided by MRI images of the monkeys’ brains that were compared to cortical partitioning schemes using Caret software⁴⁴. These observations were confirmed by physiological observations of white matter, gray matter and lumen crossings. Neurons included in the study all had spatially selective responses during the delay on the overlap and memory saccade tasks ⁴⁵ (Supplementary Fig. 1).

For 70 neurons, we recorded responses on an interleaved block of 2- and 4-choice trials. For 29 of these neurons, responses were collected on a second block of trials containing 90° control trials interleaved with either 2- or 4-choice trials.

Data analysis

We measured firing rates in several time windows defined with respect to the task epochs: before motion, early motion, and before saccades. For the first epoch, firing rates were obtained from 200–300 ms after the onset of the choice targets. An early window (170 to 210 ms after motion onset) and a late window (40–80 ms before saccade initiation) provided estimates of firing rates at the beginning and end of the decision process (Fig. 3,6). These points were established from an analysis of firing rate variance associated with the different motion stimuli and RTs (Supplementary Fig. 2b). For both 2- and 4-choice tasks, firing rate variance remained at a stable, low value until 190 ms after the onset of stimulus motion, after which it increased dramatically, reflecting the divergence of responses to different stimuli. We used a 40 ms window centered at this point, but the estimate of firing rate was nearly identical for a variety of intervals. The end of the evidence accumulation was taken to be the point at which the variance was lowest just before the saccade (Supplementary Fig. 2b), as in previous studies ². We used a 40 ms time window centered on the point corresponding to minimal variance. For analyses of firing rates around the saccade, the first 200 ms of the response to the dot motion are removed to exclude the stereotyped “dip” that is time-locked to onset of the random dot display (Fig. 2c, arrow). For the analysis of firing rate excursion and firing rate at the end of the decision, trials with RTs shorter than 450 ms were excluded.

A wide variety of interval definitions yielded nearly identical results, with one exception. Estimates of firing rate at the end of evidence accumulation were sensitive to the interval used because the firing rates change dramatically near the time of the saccade. However, the effect of choice number on firing rate excursion that we report here was present for a range of time intervals, centered up to 130 ms before the saccade (Supplementary Fig. 2c). 2- and 4-choice firing rate excursions were more similar for intervals centered at longer time points before the saccade, but these earlier time points are unlikely to correspond to the end of evidence accumulation ^2,46.

To estimate the buildup in firing rate during decision formation, we first constructed a PSTH (10 ms bins) for each neuron from responses aligned to the onset of random dot motion, excluding the epoch beginning 60 ms before saccade initiation. Buildup rate is the slope of the line fit to a PSTH in the epoch from 190–320 ms after motion onset using regression. We used an early epoch to (i) include as many trials as possible in the averages, (ii) minimize attrition of portions of trials from the averages (preceding the saccade), and (iii) minimize the potentially confounding effect of choice on the stimulus-dependent buildup rate. Analyses using different time intervals affected the reported values of buildup rate only slightly; the largest effect was on buildup rates corresponding to the highest motion strength, owing mainly to the attrition of trials with short RTs. Data from the 3.2% and 6.4% coherences were combined, as were data from the 72.4% and 76.8% coherences so that population averages would not be skewed by values associated with motion strengths used only on a minority of days.

On the 4-choice task, the buildup rates for orthogonal motion were generated from combined responses to the two orthogonal motion directions used. We obtained similar results whether buildup rates were from individual neurons (as described above) or were computed from the average population response (data not shown).

Population analyses that group trials with a common motion direction (relative to T_in), as well as the estimate of u(t), could be affected by a choice bias. We therefore analyzed the distribution of choices made on the 0% coherence motion trials. No reliable bias was found. For 2-choice trials, the number of T_in and T_out choices was 1452 vs. 1387 (p=0.22, Binomial distribution, H₀:p = 0.5). For 4-choice trials, the number of T_in, T_out, T₊₉₀, and T₋₉ was 1461, 1421, 1387, and 1426 (p=0.65, χ² test, H₀: equal proportions).

To estimate the relationship between buildup rate during decision formation and RT, we analyzed single trials (Fig. 7), using weak motion strengths (0–25.6% coherence) leading to correct T_in choices (all T_in choices for 0% coherence). We estimated firing rate on each trial by convolving the spike train with an alpha-like function (1 − e^−t/g) · e^−t/d where d=25 ms and g=1 ms. The buildup rate is the slope of the best fitting line to the smoothed firing rate in the epoch from 190 ms after motion onset to 120 ms before saccade initiation. The buildup rates and the associated RTs were standardized for each motion strength (difference from the mean in units of sample standard deviation). The standardized buildup rates and RTs were combined for all coherences to estimate a correlation coefficient (Kendall τ) for each neuron. We required that at least 3 spikes be present in a trial to estimate build-up rate and that at least 5 trials be present in a given neuron to estimate the correlation coefficient. One neuron was excluded on the 4-choice task for failing to meet these criteria. After estimating the correlation coefficient for each neuron, we tested whether the mean of the population was significantly less than 0 (t-test).

We used regression analyses to estimate the effect of the number of choices on LIP firing rates ⁷. These are referred to in the text by equation number. Unless otherwise stated, all fitting uses maximum likelihood under Gaussian assumptions for noise (weighted least squares regression with known variance); standard errors of parameter estimates were obtained by inverting the Hessian matrix of derivatives of the log likelihood with respect to the parameters, evaluated at the maximum likelihood solution. For these regression analyses, tests of significance are based on t-statistics computed from the estimated coefficients and their standard errors. For many analyses, single neuron measurements were gathered in a frequency histogram (Fig. 3c,d, 6c,d; Supplementary Fig. 1c, 4, Supplementary Fig. 5) upon which we used a t-test (effectively a paired t-test on the associated scatter plots). For all analyses, we also used maximum likelihood to generate population means and associated t-statistics. These two methods sometimes yielded slightly different estimates, but the direction and significance of all results reported here was the same for both methods.

For simple comparisons of firing rates in a specified epoch, the regression is effectively a t-test:

$$y={\beta }_0+{\beta }_1{I}_N$$ (1)

where I_N = 0 or 1 for 2- and 4-choice, respectively, and y is the spike rate on individual trials. The β_i are fitted coefficients. The null hypothesis is that choice number does not affect the firing rate(H₀:β₁ = 0).

To compare firing rate excursion for 2- verses 4-choice, we fit the model:

$$y={\beta }_0+{\beta }_1{I}_N+{\beta }_2{I}_T+{\beta }_3{I}_N{I}_T$$ (2)

where the β_i are fitted coefficients, y is the spike rate measured in the beginning and late epochs (defined above), and the I_x are indicator variables: I_N = 0 or 1 for 2- and 4-choice, respectively; I_T = 0 or 1 for early and late epochs, respectively. The coefficients estimate the following parameters: β₀ is the firing rate for 2-choice condition in the early epoch; β₀ + β₁ is the firing rate in the 4-choice condition in the early epoch; β₀ + β₂ is the firing rate in the 2-choice condition in the late epoch; and β₀ + β₁ + β₂ + β₃ is the firing rate in the 4-choice condition in the late epoch. β₂ furnishes an estimate of the firing rate excursion in the 2-choice, and ) β₃ estimates the difference in excursion on the 4- choice task. The null hypothesis that the number of choices does not affect the excursion is H₀: β₃ = 0.

To compare responses between the 2- and 4-choice tasks during the motion epoch, we computed the relationship between motion strength and buildup rate using a weighted regression:

$$y={\beta }_0+{\beta }_1{I}_N+{\beta }_{2}C+{\beta }_3{I}_{N}C$$ (3)

where y is the buildup rate either averaged across all the neurons in the population (Fig. 4f, g) or for a single neuron (Fig. 4e and Supplementary Fig. 5) for each motion strength, I_N is an indicator for the number of targets (as above) and C is motion strength (% coherence). The buildup rates associated with 0% coherence motion are furnished by β₀ and β₀ + β₁ for 2- and 4-choice tasks; β₂ and β₂ + β₃ provide estimates for the effect of a change in motion strength on the buildup rates. We express this in units of sp/s per s per unit change in motion strength (1% coherence). The null hypothesis is that the number of choices does not affect this relationship (H₀: β₃ = 0).

Eye Movements

Eye position was sampled at 1 kHz using the scleral search coil method ^47,2. To identify differences in the oculomotor responses on 2-choice verses 4-choice trials, we compared peak saccade velocity, saccade amplitude, and saccade error on each condition. Some of these measures were affected by the number of choices ^48,49 (Supplementary Fig. 8). To test whether these factors explained (as potential confounders) the effect of choice number on LIP responses, we incorporated the three significant parameters into the regression above:

$$y=\mathit{rhs}+{\alpha }_{1}S+{\alpha }_2\stackrel{.}{S}+{\alpha }_{3}E$$ (4)

where y is the spike rate measured on each trial either at the beginning or end of the decision for all trials in all cells (each trial contributes two measures), rhs is the right-hand side of equation 1 or 2; the α_I, are additional fitted coefficients; and S, Ṡ, and E are amplitude, peak velocity and endpoint error, respectively. The null hypotheses were re-evaluated with these extra terms in the regression. The null hypothesis, that the number of choices did not affect the excursion, was again rejected at the population level (p<0.01) and in all but one of the individual cells where the effect of firing rate excursion was significant. In this cell, firing rate excursion was longer for 2-choice than for 4-choice, an exception to the trend that we ordinarily observed.

Diffusion model

We fit behavioral data using an accumulator model (Supplementary Fig. 6a, d, Table 1). An accumulator corresponding to each target integrates the momentary evidence toward a decision bound. We assume the evidence is a linear combination of MT activity tuned for motion toward the targets. The linear weights were taken from the cosine of the angle difference between the directions ²². The bound height and the motion-independent signal u(t) were obtained from the neural responses to the 2- and 4-choice tasks, as explained below. Three free parameters remained to be fit: K, a scaling parameter that converts motion strength to momentary evidence (would be buildup rate if u(t) = 0); σ, the standard deviation of this momentary evidence (diffusion coefficient); and T₀, the mean nondecision time.

The fit maximized the likelihood of the observed choices and RTs for each data set (2- or 4-choice; the model performed only slightly worse when T₀ was constrained to be the same value for 2- and 4-choice conditions). These likelihoods were calculated directly using established numerical solutions ⁵⁰ to the partial differential equations (Fokker-Planck) describing diffusion to a nonstationary bound, B – û(t), where B is the initial bound height and û(t) is an estimate of the urgency signals (see below). For the 2-choice task, the race between two choice-mechanisms is equivalent to 1-dimensional diffusion with two symmetric but collapsing bounds. For 4-choice, the 4 races reduce to a race between two of the 2-choice diffusion processes. The model with urgency explains the longer RTs on error trials ³⁶ (Supplementary Fig. 7).

Urgency signals, u(t), were estimated from neural responses to 0% coherent motion. We first averaged responses to T_in and T_out trials separately. A grand average of these averages should be flat if LIP reflects only accumulated evidence. u(t) is the time-varying signal that would need to be subtracted to produce this flat response (Supplementary Fig. 6b, c). The urgency signals for each condition were parameterized separately with a hyperbolic function, $\widehat{u}(t)=u_{\infty }\frac{t}{t+{\tau }_{1/2}}$, where u_∞ is the maximum, and τ_1/2 is the time to reach 50% of the maximum. The fitted values are listed in Table 1 for each condition. In the model, this parameterized function was used to add a time-varying signal to the accumulated evidence. Parameters were optimized separately for behavioral responses in conjunction with all the recorded neurons (Table 1, top; Fig. 1d, e), and for those taken in conjunction with the 29 recording sessions when the 90° control was also presented (Table 1, bottom; Fig. 1f, g).

Supplementary Material

supp data

Supplementary Figure 1. Responses on the memory and overlap saccade tasks. These delay tasks were used as a screening procedure to establish the location of the choice targets in the motion task. Trials were also randomly interleaved with the motion task at a low frequency (~1 per 20 motion discrimination trials). The monkey maintained fixation until extinction of the fixation point and then made a saccadic eye movement to the target location to receive a reward, (a) Population average of responses on the overlap saccade task. The choice target remained visible throughout the duration of the fixation-delay period. Response averages are aligned to the onset of the target (left) and to saccade initiation (right). Cells were excluded from the graph if the target positions tested were not within 15° of the target positions used in the dot motion task, (b) Responses on the memory saccade task. The target was flashed for 115 ms and made invisible during the fixation-delay period. Same conventions as in (a), (c) Comparison of delay period activity for the T_out and T₉₀ target locations on the overlap saccade task (N=46 neurons). Average response was measured from 100 ms after the onset of the choice targets to the offset of the fixation point. The mean response to T₉₀ targets is similar to the mean response to T_out targets, suggesting that they are not in a suppressive region of the RF or its surround. Histogram displays the firing rate differences for all 46 neurons in this sample. The arrow indicates the mean difference (0.36±0.63 sp/s larger for T₉₀ choices than for T_out choices, p=0.57). Data for one neuron with a high background firing rate was omitted from the scatter plot to facilitate an appropriate scale for the remaining points {36.4,46.2}. Data are from experiments in which reliable recordings were obtained for the 4 target positions used in the motion task. Neurons were excluded if they lacked a sufficient number of trials at both orthogonal and opposite positions to estimate an average response.

Supplementary figure 2. Justification of the analysis epoch corresponding to termination of the decision, (a) Responses grouped by RT suggest a termination “bound” on the 2-choice task. Responses for correct trials ending in T_in choices are aligned to saccade initiation. Responses are grouped by RT in 50 ms bins (indicated by color); the average response of every other bin is plotted. The corresponding graph for the 4-choice task is in Figure 2d of the main text. The graphs support the existence of a bound in firing rate that marks the termination of trials. However, it is difficult to estimate when firing rates reach a common value because they continue to rise until ~10 ms before saccade initiation, on average. Based on the 4 traces shown, the rates seem to reach a common endpoint between 40–80 ms before the saccade. Gray shading indicates the window we used in our analyses of these endpoints (same 40 ms window for 2- and 4-choice tasks), (b) Examination of response variance. The graphs show the portion of the response variance that can be attributed to the RT groups. This analysis uses all the RT groups, including those not shown in (a) and Fig. 2d. The sample variance was estimated using non-overlapping bins (width = 20 ms). The variance associated with RT groups reached a nadir in the interval 40 to 80 ms before the saccade. This is the window used for our analysis of firing rate excursion, (c) Firing rate excursions were significantly larger for 4-choice than for 2-choice responses over a wide range of termination intervals. This graph exposes the degree to which one of our conclusions rest on the choice of termination interval. Each point is the difference between firing rate excursions on the 2- and 4-choice tasks obtained by using the 40 ms wide termination interval centered at the value on the abscissa (combined data from the two monkeys). The excursion is the difference in firing rate in this window from the firing rate at the beginning of the decision, 170 to 210 ms after the onset of stimulus motion. The red circle indicates the estimate of firing rate excursion that was reported in the main text and used in the model fits of behavioral choice and RT. Error bars are s.e.; asterisks indicate significant differences in excursion for 2- and 4-choice tasks. Although magnitude of the difference in excursion depends on the choice of termination window, the central claim that excursion is larger on the 4-choice task appears robust.

Supplementary Figure 3. Difference in firing rates for 2- and 4-choice trials at the beginning of the motion viewing period. Points represent mean firing rates from single neurons in an epoch 170 to 210 ms after the onset of stimulus motion. One point, {171,120}, corresponding to a neuron with high background firing rate, is omitted from the plot to facilitate an appropriate scale for the remaining points. The histogram shows differences between 2- and 4-choice trials (N=70 neurons). Shaded bars indicate significant cases (p<0.05). The arrow indicates the mean difference (9.2±1.1 sp/s larger for 2-choice trials, p<10⁻⁵). This difference is similar in magnitude to the one seen in the epoch preceding onset of random dot motion (Fig. 3, main text).

Supplementary Figure 4. Motion strength affects the buildup rates even for trials that terminate with the same saccadic choice. This analysis is identical to the one in Figure 4 of the main text, with one exception. Here, all averages are calculated for trials that end in the same choice. For nonzero coherence motion these are the correct choices only. By selecting only one set of choices, this analysis produces a biased estimate of the effect of motion strength on buildup rate. Importantly, however, it demonstrates that the effect of motion strength on buildup rate is not explained by averaging over different proportions of correct and error trials. Plotting conventions are otherwise identical to Figure 4.

Supplementary figure 5. Similarity of motion-dependent buildup rates in the 2- and 4-choice tasks. These single-neuron analyses complement the analyses shown in Figure 4 of the main text, (a) Comparison of the effect of motion in the T_in direction on buildup rates. Each point plots the slope of the best fitting line relating response buildup rate to motion strength for a single neuron (N=70 neurons). The buildup rates were estimated using regression of firing rate vs. time in the interval 190–320 ms after the onset of stimulus motion. The buildup rates and their s.e. were then used as the dependent variables in a second regression against motion strength. The slope of this line furnishes the change in buildup rate per unit change in motion strength (see Methods). Stronger motion was associated with larger buildup rates (note the positive slopes). Error bars are s.e. of buildup rate and are occasionally obscured by the points. The histogram shows differences between 2- and 4-choice trials. Shading indicates significant cases (p<0.05). The magnitude of the coherence-dependent change was similar for 2- and 4-choice conditions (mean difference = 0.02±0.03 sp·s⁻²·% coh⁻¹, p=0.53, arrow). The solid line is the main diagonal (x=y). (b) Comparison of the effect of motion in the T_out direction on buildup rates. Same conventions as in (a). Stronger motion was associated with lower buildup rates (note the negative slopes). The magnitude of the coherence-dependent change of buildup was greater in the 2-choice task (mean difference = 0.075±0.021 sp·s⁻²·%coh⁻¹ less negative for 4-choice trials, p<0.001).

Supplementary Figure 6. Race model of bounded evidence accumulation. The panels furnish intuitions about the process that is thought to underlie decisions on the 2- and 4-choice tasks as well as the model used to fit the behavioral data, (a) Simulated decision variables for a pair of example trials for 2- and 4-choice tasks in which motion in the up-right direction leads to a correct choice. Momentary evidence arising from direction selective neurons is combined and accumulated into 2 or 4 decision variables (DV) depicted by the black and red traces, respectively. These DVs represent the accumulation of evidence for each of the choices. These examples exclude the “urgency” signal. Except for this omission, they would approximate the firing rates of LIP neurons, beginning 190 ms after motion onset, just following the dip. The decision terminates when one DV reaches a threshold level, termed the bound (horizontal line), which determines the choice and the decision time. The RT is the decision time plus a nondecision time (Normally distributed with mean T₀ and standard deviation $\frac{1}{3}$ T₀). For decisions between 2 opposite directions, the momentary evidence is thought to be a difference in firing rates of direction selective neurons with opposite direction preferences. At each moment, this difference is a random number drawn from a Normal distribution (inset) whose mean depends on the strength and direction of motion (meaN=K · C, where C is motion strength) and standard deviation σ (K,σ and T₀ are fitted parameters; see Table 1). In this example, the expectation is in favor of up and right. The process depicted at the top right accumulates these random numbers in favor of its T_in. The accumulation increases on average and also in the pair of examples shown, which reach the bound and thereby terminate the decision for up-right. The process at the bottom left accumulates evidence for the down-left target. This accumulation decreases on average (and in these examples) for up-right motion. The two trials end with a choice corresponding to this “neuron’s” T_out In the 4-choice task, the form of the momentary evidence is not known. In the model used to fit the behavior, we assume that direction sensors with orthogonal preferences do not contribute substantially to the mean accumulation. The up-right motion in this example does not bias the evidence accumulated by the up-left and down-right processes. These processes accumulate momentary evidence with zero-mean. The DV undergoes a larger excursion in the 4-choice task because the accumulation of evidence begins at a lower starting point, (b) “Urgency” signals in 2-choice (black) and 4-choice (red) tasks. We observed a time-dependent buildup of firing rate that is not explained by evidence accumulation. This is the buildup seen on 0% coherence motion trials, when the momentary evidence is unbiased for T_in or T_out The traces are formed by averaging the firing rates for T_in and T_out choices, respectively, and then making a grand average of these averages. (Nearly identical results are obtained using a simple average across all T_in and T_out trials at 0% motion strength, because the monkeys were unbiased in their choices on these trials in all three tasks.) Thin lines are fits of a hyperbolic function (see Methods) to the responses, beginning 190 ms after motion onset, when evidence accumulation is first reflected in LIP. These “urgency” functions, û(t), were incorporated as constraints in the bounded accumulation model fit to the behavioral data (Fig. 1d–g, Supplementary Fig. 7). Similar urgency signals are observed on trials with nonzero motion strengths (data not shown). (c) Same as in (b) except that urgency signals were estimated from the subset of experiments where the 90° control (blue) was performed. For the 90° control, û(t) was estimated by taking the grand average of the average responses to T_in and T₉₀ motion, (d) Same examples as in (a) with the urgency signals from (b) added to the accumulations. The urgency signal shortens the RTs and leads to an apparent rise in the DV even for processes that accumulate negative evidence.

Supplementary figure 7. The bounded accumulation model explains the RTs measured on error trials. This figure complements the psychometric and chronometric functions shown in Figure 1 of the main text. Smooth curves in panels and inserts are fits to the bounded accumulation model described at the end of Results. Points are from the data (N=70 neurons); error bars are s.e.m. (some are smaller than the symbols), (a) RTs on correct and error trials on the 2-choice task. Insert depicts error rates expressed as proportion of trials. For 0% coherent motion, half the trials are defined arbitrarily as errors; this is really the guess rate, (b) RTs on correct and error trials on the 4-choice task. The errors are shown separately for choices opposite (180°) and neighboring (± 90°) the true direction of motion. Insert depicts rates for the two types of error. For 0% coherent motion, % of the trials are defined as errors. The rates are ¼ for 180° choices and ½ for the combined±90° choices. According to the model, the longer RT on errors arises as a consequence of the urgency signal, u(t), which effectively imposes a more lax criterion for terminating the decision (as if the bound were dropping as a function of time), thereby rendering errors more frequent³⁶.

Supplementary Figure 8. Comparison of oculomotor responses on the 2- and 4-choice tasks, (a–c) Samples of eye movements recorded during one experiment. Only correct T_in choices are shown. These traces illustrate the degree of variation observed typically in our experiments, (a) Sample trajectories, aligned to the time corresponding to peak eye velocity, from the 2-choice (black, N=10) and 4-choice (red, N=10) tasks. Eye position is along the vector from fixation to T_in. Amplitude is the difference in average position measured in epochs 40–100 ms before and after the saccade. (b) Eye velocity trajectories, aligned to the time corresponding to peak eye velocity, from the 2-choice (black) and 4-choice (red) tasks. Velocity is along the vector from fixation to T_in. Same examples as in (a), (c) Variation in saccadic end points on the 2-choice (black, N=25) and 4-choice (red, N=25) tasks. Error magnitude was computed as the distance between the saccade endpoint and the choice target (blue circle), (d–f) Systematic variation in saccade metrics on 2- and 4-choice tasks. For each neuron, we obtained averages for amplitude, peak velocity, and error magnitude for T_in choices on the 2 and 4-choice tasks. Histograms depict the differences in these averages, expressed as a percentage variation with respect to the mean for 2- and 4-choice conditions (positive values imply a larger value for the 2-choice condition; shading indicates significance, p<0.05, see Methods, Eq. 4). Records are from 40 neurons. Permanent records of eye position were lost for the remaining neurons, (d) Saccade amplitudes. Reliable differences favoring either the 2- or 4-choice condition were observed in many experiments, but the overall difference was negligible across our sample (mean percent difference = −0.59±0.46%; p=0.212). (e) Saccadic peak velocity. Again, reliable differences of both signs (higher/lower velocity) were seen in individual experiments, and the trend was for slightly faster saccades on the 4-choice task (mean percent difference = −1.37±0.5%, p<0.01). (f) Error magnitude. Reliable differences of both signs (larger/smaller errors) were seen in individual experiments. The trend was for less accurate saccades on the 4-choice task (mean percent difference = −4.87±2.03% p<0.03). Note that although the percent difference in error magnitude was sometimes considerable, the mean error magnitude was only 1.41±0.1°. The differences displayed in the histogram are expressed as a fraction of this small magnitude.