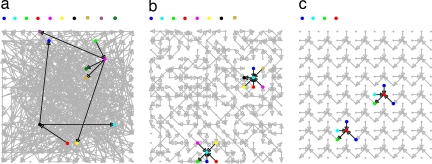
Fig. 1.

The number of addresses required to wire geometric networks is smaller than the number required to wire arbitrary networks. All networks have 225 nodes and a mean connectivity of two edges per node. Addresses are depicted by colors. The addresses of the two highlighted nodes and their connected neighbors in each figure are shown above each image. (a) An arbitrary Erdős–Rényi network in which all nodes can connect to each other requires 218 addresses. (b) A 2D geometric network with a neighborhood size of D = 9 nodes requires only 38 addresses. (c) An ordered geometric network in which the same connectivity pattern in a neighborhood of size D = 9 is iterated throughout the network. The network requires 12 addresses. The geometric networks shown have noncontinuous boundary conditions for clarity.